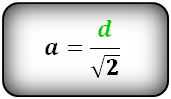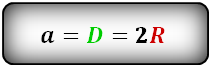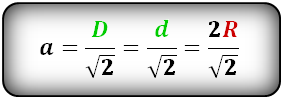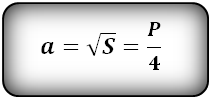Задача
о нахождении стороны квадрата.
Выполните задания.
1. Запишите формулу вычисления площади квадрата.
 |
2. Найдите площадь квадрата, если его сторона равна:
а) 3 см; б) 4 см; в) 5 м; г) 6 мм; д) 7 км; е) 8 дм
3. Заполните таблицу:
|
a |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a2 |
Если известна сторона
квадрата, то можно найти площадь по формуле S
= a2.
А если, наоборот, известна площадь, как найти сторону квадрата?
Можно подобрать
соответствующее число а, что
S
= a2.
Такое действие
записали с помощью знака радикала
. Его называют знаком квадратного корня.
Получается формула .
Если S = 64 = 82, то а = 8. Значит .
Такое действие
называют извлечение квадратного корня из числа 64, число под знаком радикала
называют «подкоренное число».
4. Заполните таблицу:
|
S |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
|
5. Найдите значение (используйте
в помощь таблицу квадратов двузначных чисел на форзаце в начале учебника)
Итак,
, потому что 232
= 529
В классе: № 225 (б,в,д,е,з,и), 226 (б,г,е),
227 (б,г,е,з,к), 231
Домашнее задание: п. 2.1, № 225 (а,г,ж), 226 (а,в,д), 227
(а,в,д,ж,и), 229
МОУ «СОШ № 2 г. Калининска Саратовской области».
Урок
математики в 8 классе.
Учитель: Шманова Г.Ю.
2010-2011 уч. год
Алгебра 8 кл.
Тема урока: «Задача о нахождении стороны квадрата».
Цели:
Образовательная: знать определение квадратного корня, учиться выполнять преобразования с квадратными корнями;
Развивающая: развивать сознательное восприятие учебного материала; познавательной активности, интереса к предмету.
Воспитательная: воспитание культуры общения; точности в записи решения примеров.
Ход урока:
Пусть каждый день и каждый час
Вам новое добудет.
Пусть добрым будем ум у вас,
А сердце умным будет. (Приложение 1)
- Орг. момент.
- Повторение изученного материала.
- Устный счёт.
1. Вычислите
(-2); 3
; 0,7
; 2
; (-1)
; (-1)
2. . Дано: квадрат,
а) а = 6 см,
б) а = 11 см.
Найти: S. Ответ: а) 36 см2, б) 121 см2.
3. Дано: квадрат,
а) S = 25 см2,
б) S = 81 см2.
Найти: а. Ответ: а) 5 см, б) 9 см.
Б) Математический диктант:
- Что называют стандартным видом числа?
(Стандартным видом числа называют его запись в виде произведения 10n, где 1 < 10 и n – целое число).
(Приложение 1).
- Запишите с помощью букв свойства степени с целым показателем.
(Для любого а0 и любых целых m и n:
am an = am + n;
am : an = am – n;
(am)n = amn;
(Приложение 1(а)).
Для любых а0 и b0 и любого целого n:
(ab)n = a nbn;
()n .
(Приложение 1 (б)).
3. Площадь квадрата равна 49 м2. Найдите длину стороны квадрата.
(а = 7 м.).
- Изучение новой темы.
Если известна длина стороны квадрата, то можно найти его площадь. В то же время приходится решать и обратную задачу – по известной площади квадрата находить его сторону.
Например, если площадь квадрата 100 см2, его сторона равна 10 см. Мы подобрали число, квадрат которого равен заданному значению площади. Таких чисел, вообще говоря, два: 10 и -10. Но мы, естественно, взяли то из них, которое является неотрицательным, – ведь отрицательным числом длина выражаться не может!
Если сторона квадрата равна a, то его площадь S можно вычислить по формуле S = a2. Но в математике есть также способ и для выражения стороны квадрата через его площадь. Чтобы записать соответствующую формулу, нам придётся ввести новый символ: . Этим символом обозначена сторона квадрата, площадь которого равна S. Иными словами, – это неотрицательное число, квадрат которого равен S. Знак называют знаком квадратного корня или радикалом (от латинского слова radix – корень), а читают выражение так: квадратный корень из S.
С использованием введённого символа формула для нахождения стороны квадрата a, площадь которого равна S? Запишется следующим образом:
a = .
Пусть, например, S = 64. Тогда a = . Так как 64 = 82, то = 8. Мы заменили выражение его значением – числом 8, или, как говорят, извлекли квадратный корень из 64.
В приведённом примере нам нетрудно было найти значение корня. Однако если подкоренное число большое, то для извлечения корня приходиться пользоваться вспомогательными приёмами.
Пример 1. Найдём .
Чтобы подобрать число, квадрат которого равен 2304, обратимся к таблице квадратов двузначных чисел (см. стр. 254). Из таблицы видно, что 2304 = 482. Значит, = = 48.
Пример 2. Найдём .
Так как под корнем пятизначное число, то таблица квадратов двузначных чисел нам уже не поможет. Поэтому воспользуемся другим приёмом – разложим число 15876 на множители.
Так как 15876 = 22 34 72 = (2 9 7)2, то = = 2 9 7 = 126.
При записи выражений, содержащих радикалы, так же как и других алгебраических выражений, нужно придерживаться некоторых правил. Так числовой или буквенный множитель пишут перед радикалом, например 2, a.
Знак корня, как и скобки, является группирующим символом. Если, например, нужно найти значение выражения , то сначала надо вычислить сумму 42 +32, а затем извлечь корень: = = = 5.
- Закрепление.
- Фронтальный опрос.
- Запишите формулу для нахождения стороны квадрата a по его площади S. (a = ).
- Что обозначают символом ? (Этим символом обозначена сторона квадрата, площадь которого равна S).
- Найдите , если S = 25; 36; 0,01. (5; 6; 0,1).
- Решение задач.
№ 217 Вычислите:
б) = 6.
з) = 0,7.
№ 218 Вычислите:
а) = .
е) = .
№ 219 Вычислите, пользуясь таблицей квадратов двузначных чисел:
д) = 32.
з) = .
Самостоятельная работа.
Три уровня сложности по возрастающей – на выбор учащегося.
1 вариант
|
х |
25 |
0,36 |
|
0,0001 |
-16 |
2+ |
256 |
|
|
|
2 вариант
|
а |
3 |
9 |
-7 |
36 |
-13 |
-11 |
2 |
|
|
в |
6 |
16 |
11 |
64 |
-12 |
11 |
|
|
|
|
3 вариант
|
а |
4 |
0 |
5 |
10 |
12 |
|
|
|
в |
0 |
-6 |
-12 |
24 |
9 |
2 |
-6 |
|
|
№ 1. Выполнение теста:
Запишите значение при а, равном
а) а = 1
1) 0,1 2) -1 3) 1 4) 10.
б) а = 144
1) 144 2) 14 3) 12 4) 21.
в) а = 0,04
1) 0,4 2) 2 3) 0,2 4) 4.
Ответы: а ) 3); б) 3); в) 3)
№ 220 Найдите значение выражения при заданных значениях переменной:
б) x = ; ; . (; ; ).
№ 221 Верно ли, что:
б) = 0,18. (Да).
г) = 0,31. (Нет).
№ 222 Запишите равенство, связывающие данные числа, не используя знак :
г) = 0,21. (0,0441 = 0,212).
№ 223 Запишите соотношение, между данными числами с помощью знака :
б) 412 = 1681. (41 =).
№ 224 Вычислите:
г) = 12,56.
№ 225 Вычислите:
г) = 1600.
Вычислите устно: (Физминутка)
а)=
б) =
в) =
д) =
к)=
л) =
м)+
=
- Подведение итогов.
Всё в этом мире взаимосвязано: математика, русский язык и литература, биология, так как слово “корень” встречается на уроках математики, биологии, русского языка.
Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал сегодня?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал сегодня?» и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием. «А я принимал участие в строительстве храма».
- Ребята, кто работал так, как первый человек, положите руки на стол.
- Кто работал как второй человек, поднимите правую руку?
- Кто принимал участие в строительстве храма, поднимите обе руки.
РЕФЛЕКСИЯ.
Продолжите предложения:
- Сегодня на уроке математики я…»
- «Мне было не сложно выполнять задания, потому что…».
« Вам было не сложно выполнять задания, потому, что вы имеете хорошие знания по данной теме».
- Домашнее задание: п. 2.1; стр. 55 – 56; №№. 217 – 225 (все под (в)).
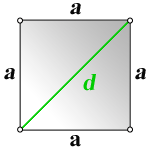
1. Формула стороны квадрата через диагональ
a – сторона квадрата
d – диагональ квадрата
Формула стороны квадрата, (a):
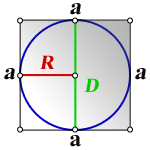
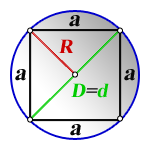
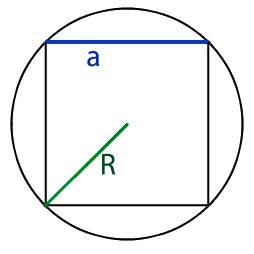
2. Формула стороны квадрата через радиус вписанной окружности
a – сторона квадрата
R – радиус вписанной окружности
D – диаметр вписанной окружности
Формула стороны квадрата, (a):
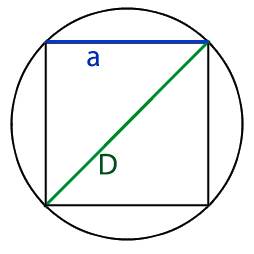
3. Формула стороны квадрата через радиус описанной окружности
a – сторона квадрата
R – радиус описанной окружности
D – диаметр описанной окружности
d – диагональ
Формула стороны квадрата, (a):
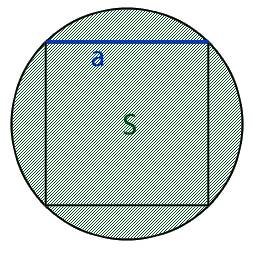
4. Формула стороны квадрата через площадь и периметр
a – сторона квадрата
S – площадь квадрата
P – периметр квадрата
Формула стороны квадрата, (a):
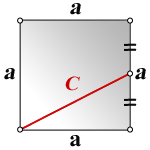
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a – сторона квадрата
C – линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
- Подробности
-
Опубликовано: 13 октября 2013
-
Обновлено: 13 августа 2021
Квадрат – это четырёхугольная плоская геометрическая фигура с равными сторонами. Квадрат считается
прямоугольником, так как все его внутренние углы по 90°. Диагонали правильного четырёхугольника
равны между собой, пересекаются под прямым углом и делятся точкой пересечения пополам. А также они
являются биссектрисами внутренних углов (отрезок делит прямой угол на два одинаковых угла по 45°).
Знание и применение этих свойств позволяют быстро решать задачи по геометрии. Ромб с равными
диагоналями, ромб с двумя соседними прямыми углами, параллелограмм с одинаковыми диагоналями,
пересекающимися под прямым углом, все эти фигуры являются правильными четырёхугольниками.
- Сторона квадрата через радиус вписанной окружности
- Сторона квадрата через радиус описанной окружности
- Сторона квадрата через площадь квадрата
- Сторона квадрата через диагональ
Через радиус вписанной окружности
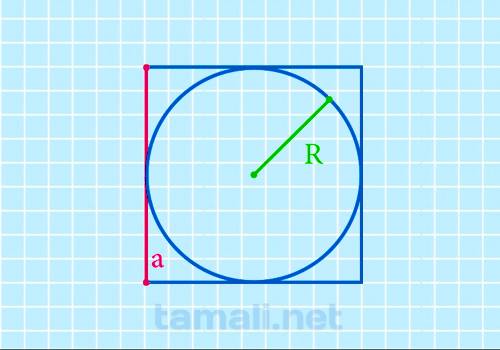
Длина стороны равна двум радиусам (диаметру) вписанной окружности:
a=2*R
где R — радиус.
Цифр после
запятой:
Результат в:
Радиус – это расстояние от центра окружности до любой ее точки. Диаметр — отрезок, соединяющий
две любые точки окружности и проходящий через центр. Радиус составляет 1/2 диаметра. Все стороны
правильного четырёхугольника являются касательными прямыми к вписанной окружности. Радиус всегда
перпендикулярен касательной. Вписанная окружность делит точкой касания стороны квадрата на две
равные части. Зная величину диагонали, одинаковую длину стороны и диаметра легко можно объяснить
благодаря теореме Пифагора: «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов». В данном случае если построить отрезки, соединяющие противоположные вершины правильного
четырёхугольника, образуется равнобедренный прямоугольный треугольник, где половина стороны квадрата
и радиус являются катетами, а половина диагонали — гипотенузой.
Формула вычисления через площадь
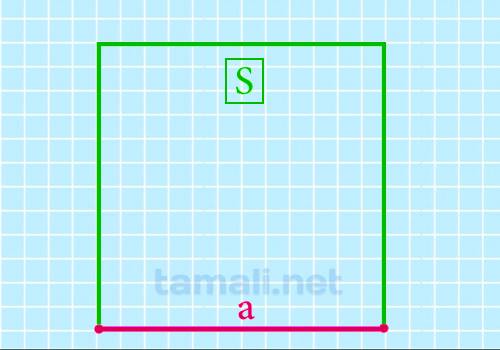
Для того чтобы определить длину стороны, зная только площадь, нужно извлечь квадратный корень из
известного значения:
a=√S
где S — площадь.
Цифр после
запятой:
Результат в:
Это самый простой способ. Площадь плоской четырёхугольной геометрической фигуры – это числовое
значение, которое характеризует размер плоскости, ограниченной четырьмя сторонами. Для нахождения
площади прямоугольника необходимо умножить длину на ширину, для площади прямоугольника с равными
сторонами – возвести длину в квадрат.
Также есть и другие способы для нахождения площади правильной
четырёхугольной фигуры: через радиус вписанной или описанной окружности, периметр, через длину
отрезка, проведенного из вершины к середине противоположной стороны. Если площадь неизвестна, но
есть данные о диагонали, можно легко найти воспользоваться доступной величиной — возвести
длину отрезка в квадрат и разделить на два S=d²/2.
Этот метод также
опирается на теорему Пифагора. Поделив сумму квадратов катетов на два, можно найти площадь. Однако в
этом случае значение не понадобится для нахождения стороны, можно быстро вычислить длину катета при
помощи следующей формулы.
Вычисление через диагональ
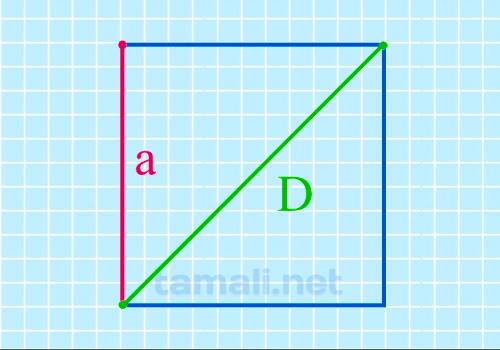
Если в задаче изначально известна длина диагонали, можно значительно сократить маршрут поиска нужной
величины. На основе этого правила сторона вычисляется по формуле:
a=d/√2
где d — диагональ.
Цифр после
запятой:
Результат в:
Через радиус описанной окружности
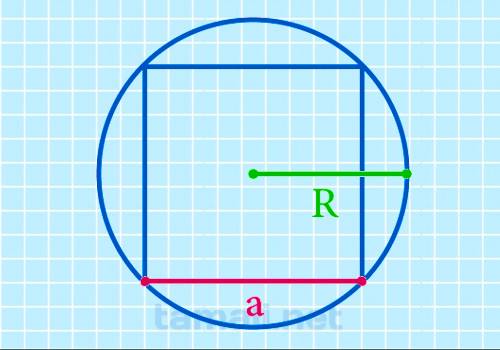
Известно, что диаметр описанной окружности равен диагонали, так как он совпадает с отрезком,
соединяющим вершины двух противоположных углов, а эти вершины являются точками окружности. Формула
для вычисления:
a = √2 * R
где R — радиус.
Цифр после
запятой:
Результат в:
Благодаря радиусу можно найти длину диагонали, которая делит фигуру на 2 прямоугольных равнобедренных
треугольника и при помощи теоремы Пифагора найти нужную величину.
Диагональ представляет собой линию, которая соединяет две вершины противоположных углов, тем самым
разделяя правильный четырёхугольник на два равнобедренных прямоугольных треугольника. Найти значение
таким способом не сложнее, чем через площадь. Главное, знать теорему Пифагора и уметь ею
пользоваться, это самый быстрый вариант. В задачах с прямоугольными фигурами теорема часто служит
выходом из сложной ситуации.
Все вычислительные способы связаны между собой. Запомнить нужные формулы несложно. Достаточно
применять их на практике каждый день, частое использование одних и тех же алгоритмов приведет к
автоматическому запоминаю правил. Не стоит заучивать формулы, необходимо больше рассуждать
логически. Такой подход позволит решать задачи более сложного уровня и легче воспринимать любую
информацию. Самым действенным методом для запоминания является практика. Отработка нескольких
идентичных задач на определенное правило поможет закрепить результат на долгий срок.
Все формулы стороны квадрата
1. Формула стороны квадрата через диагональ
a – сторона квадрата
d – диагональ квадрата
Формула стороны квадрата, ( a ):
2. Формула стороны квадрата через радиус вписанной окружности
a – сторона квадрата
R – радиус вписанной окружности
D – диаметр вписанной окружности
Формула стороны квадрата, ( a ):
3. Формула стороны квадрата через радиус описанной окружности
a – сторона квадрата
R – радиус описанной окружности
D – диаметр описанной окружности
d – диагональ
Формула стороны квадрата, ( a ):
4. Формула стороны квадрата через площадь и периметр
a – сторона квадрата
S – площадь квадрата
P – периметр квадрата
Формула стороны квадрата, ( a ):
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a – сторона квадрата
C – линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, ( a ):
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
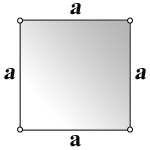
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
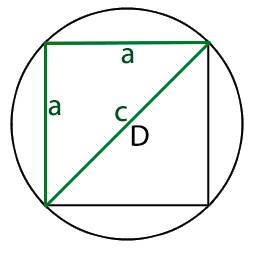
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 . . |
(1) |
Из равенства (1) найдем d:
 . . |
(2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 |
(3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 |
(4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
(5) |
Из формулы (5) найдем R:
 |
(6) |
или, умножая числитель и знаменатель на 
 . . |
(7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 . . |
(8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 |
(9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 |
(10) |
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 |
(12) |
Эти реугольники также равнобедренные. Тогда
Из (13) следует, что
 |
(14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
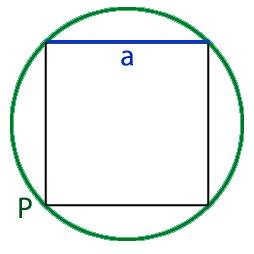
Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.
Вычислить длину стороны вписанного квадрата через:
Радиус круга R:
Для того что бы найти длину стороны вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
[spoiler title=”источники:”]
http://matworld.ru/geometry/kvadrat.php
http://tamali.net/calculator/inscribed/square/edge/
[/spoiler]