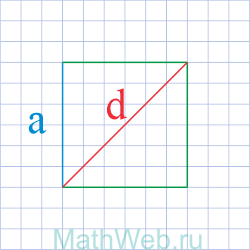
Где d – диагональ квадрата.

Где S – площадь квадрата
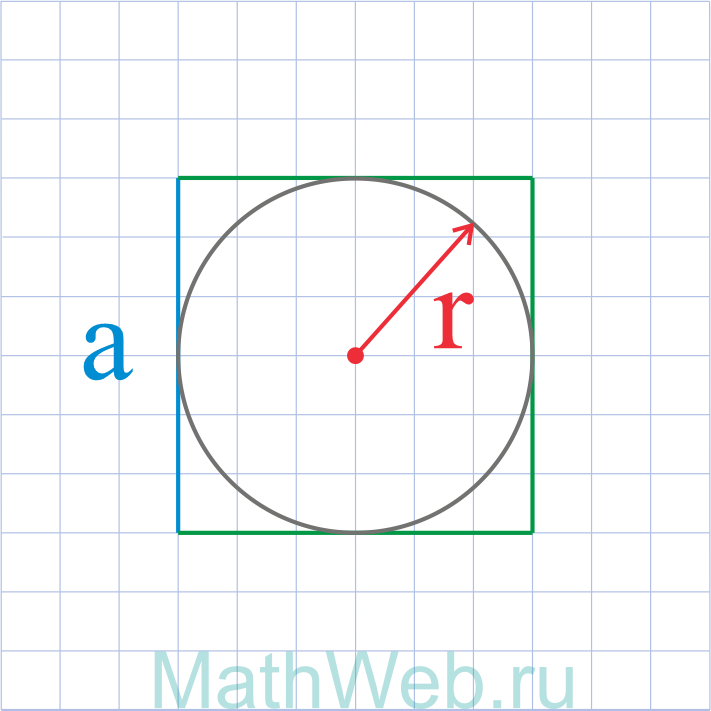
Где r – радиус вписанной окружности
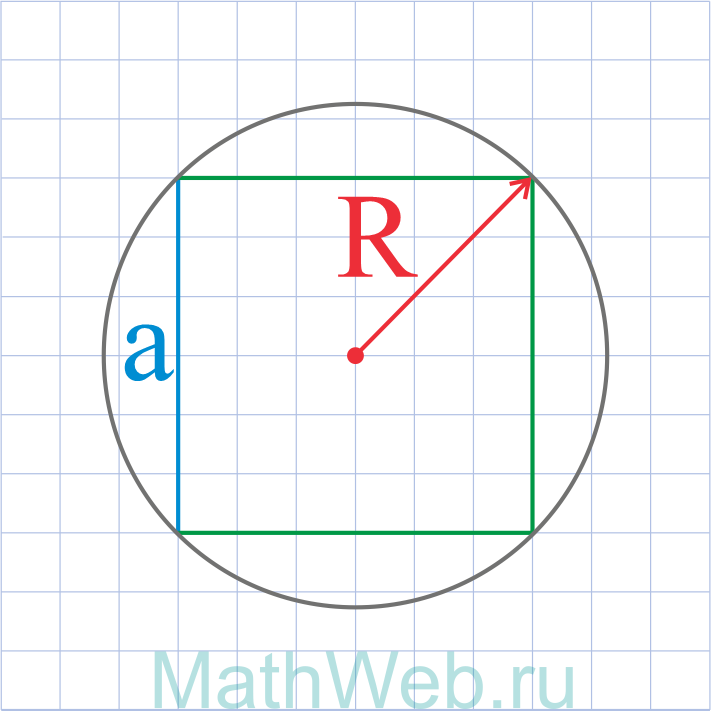
Где R – радиус описанной окружности
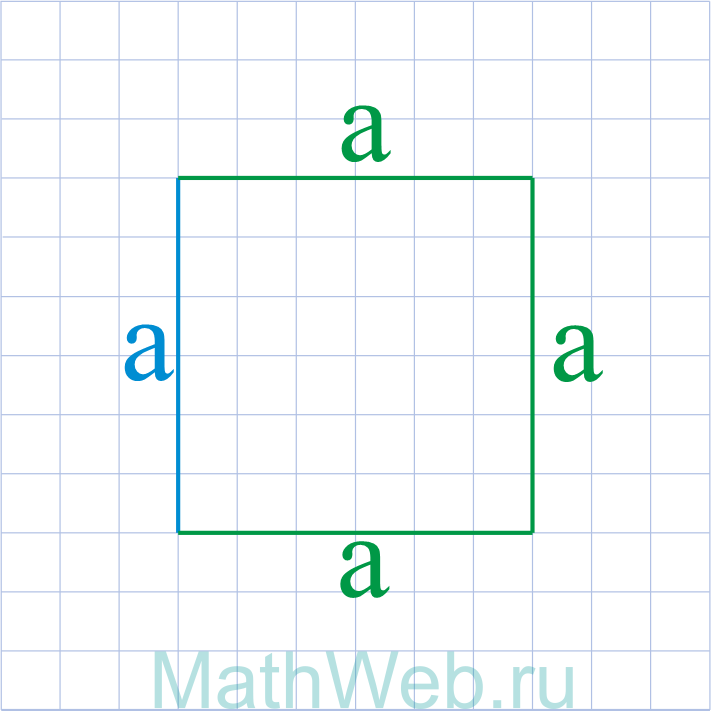
Где P – периметр квадрата.
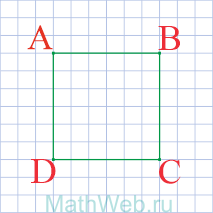
- Квадрат – это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные – перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = |
 |
a = √S |
 |
a = 2r |
 |
a = R√2 |
 |
a = |
1. Формула стороны квадрата через диагональ
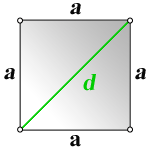
a – сторона квадрата
d – диагональ квадрата
Формула стороны квадрата, (a):
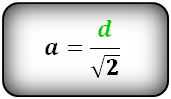
2. Формула стороны квадрата через радиус вписанной окружности
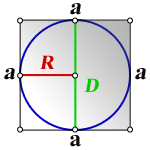
a – сторона квадрата
R – радиус вписанной окружности
D – диаметр вписанной окружности
Формула стороны квадрата, (a):
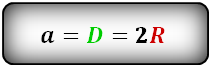
3. Формула стороны квадрата через радиус описанной окружности
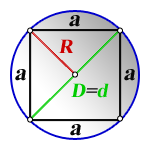
a – сторона квадрата
R – радиус описанной окружности
D – диаметр описанной окружности
d – диагональ
Формула стороны квадрата, (a):
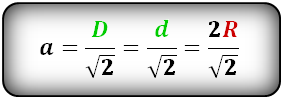
4. Формула стороны квадрата через площадь и периметр
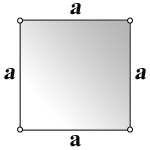
a – сторона квадрата
S – площадь квадрата
P – периметр квадрата
Формула стороны квадрата, (a):
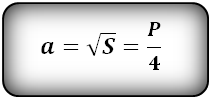
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
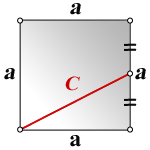
a – сторона квадрата
C – линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):

Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
- Подробности
-
Опубликовано: 13 октября 2013
-
Обновлено: 13 августа 2021
Как найти сторону квадрата, если известен периметр
Периметром называют общую длину всех сторон геометрической фигуры. Обычно его находят методом сложения размеров сторон. В случае с правильным многоугольником периметр можно найти, умножив длину отрезка между вершинами на количество таких отрезков. Именно к такому виду многоугольников относится квадрат. Зная его периметр, можно с помощью одного лишь арифметического действия найти длину его стороны.

Вам понадобится
- -калькулятор.
Инструкция
Рассмотрите любой квадрат. Вспомните его свойства. У него 4 стороны, причем все они одинаковы по длине и расположены по отношению друг к другу под прямым углом. Обозначьте сторону квадрата как а, а периметр — как р.
Вспомните, как найти размер части любого объекта, если эти части равны, а количество их вам известно. Это можно сделать, разделив целое на количество частей. Представьте периметр как целый объект, тогда каждая сторона будет его частью. Всего этих частей четыре. То есть размер стороны можно найти, разделив периметр на 4. Выразить это можно формулой a=p/4.
Точно таким же образом, зная периметр, можно найти размер стороны любого правильного многоугольника. Для пятиугольника справедлива формула а=р/5, для шестиугольника — а=р/6 и т. д.
Подумайте, у какого еще многоугольника 4 стороны, и при том они равны между собой. Это ромб, частным случаем которого многие математики считают квадрат. У ромба углы, принадлежащие одной стороне, не равны между собой, но для вычисления периметра это не играет никакой роли. Сторону любого ромба можно найти точно так же, как и сторону квадрата, то есть разделив периметр на 4.
Зная периметр квадрата, можно найти еще несколько размеров, важных для этой геометрической фигуры. Сделайте дополнительное построение, вписав в квадрат окружность. Проведите диаметр так, чтобы он соединил точки касания окружности с противолежащими сторонами квадрата. Диаметр равен стороне этой геометрической фигуры. А это значит, что и его можно найти точно тем же способом, то есть разделив периметр на 4. Выразить это можно формулой d=p/4.
В задачах очень часто требуется не диаметр окружности, а ее радиус. Найти его можно, разделив диаметр на 2. А если попытаться выразить радиус через периметр, получится формула r=d/2=(p:4)/2=р/8.
Через периметр можно выразить и радиус описанной окружности. Постройте ее и проведите радиус, который пересечет окружность в одной из вершин квадрата. Из центра окружности проведите перпендикуляр к одной из сторон данного угла. У вас получился прямоугольный треугольник, у которого к тому же равны катеты, а один еще и является радиусом вписанной окружности, то есть его размер равен р/8. Радиус описанной окружности представляет собой гипотенузу этого треугольника, и найти ее можно по теореме Пифагора, то есть R^2=(p/8)^2+(p/8)^2=2(p/8)^2.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Периметр (P) = 10
Cторона, диаметр вписанной окружности (L) = (frac{P}{4}) = (frac{10}{4}) = 2.5
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*2.5^{2}}) = 3.54
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{2.5}{2}) = 1.25
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{3.54}{2}) = 1.77
Площадь (S) = (L^{2}) = (2.5^{2}) = 6.25
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):

Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:

Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a2+a2=d2
2a2=d2

