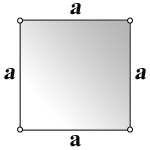
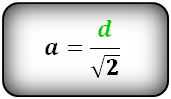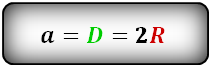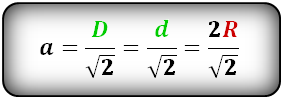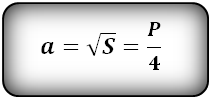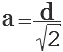Квадрат – это четырёхугольная плоская геометрическая фигура с равными сторонами. Квадрат считается
прямоугольником, так как все его внутренние углы по 90°. Диагонали правильного четырёхугольника
равны между собой, пересекаются под прямым углом и делятся точкой пересечения пополам. А также они
являются биссектрисами внутренних углов (отрезок делит прямой угол на два одинаковых угла по 45°).
Знание и применение этих свойств позволяют быстро решать задачи по геометрии. Ромб с равными
диагоналями, ромб с двумя соседними прямыми углами, параллелограмм с одинаковыми диагоналями,
пересекающимися под прямым углом, все эти фигуры являются правильными четырёхугольниками.
- Сторона квадрата через радиус вписанной окружности
- Сторона квадрата через радиус описанной окружности
- Сторона квадрата через площадь квадрата
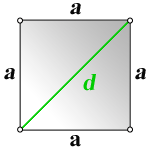
- Сторона квадрата через диагональ
Через радиус вписанной окружности
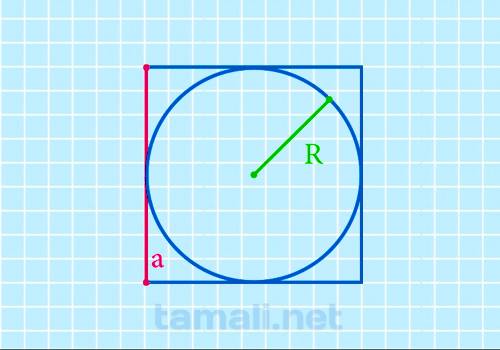
Длина стороны равна двум радиусам (диаметру) вписанной окружности:
a=2*R
где R — радиус.
Цифр после
запятой:
Результат в:
Радиус – это расстояние от центра окружности до любой ее точки. Диаметр — отрезок, соединяющий
две любые точки окружности и проходящий через центр. Радиус составляет 1/2 диаметра. Все стороны
правильного четырёхугольника являются касательными прямыми к вписанной окружности. Радиус всегда
перпендикулярен касательной. Вписанная окружность делит точкой касания стороны квадрата на две
равные части. Зная величину диагонали, одинаковую длину стороны и диаметра легко можно объяснить
благодаря теореме Пифагора: «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов». В данном случае если построить отрезки, соединяющие противоположные вершины правильного
четырёхугольника, образуется равнобедренный прямоугольный треугольник, где половина стороны квадрата
и радиус являются катетами, а половина диагонали — гипотенузой.
Формула вычисления через площадь
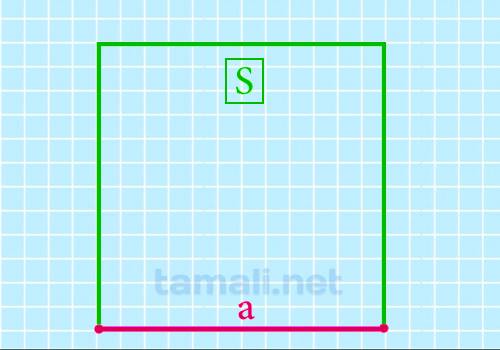
Для того чтобы определить длину стороны, зная только площадь, нужно извлечь квадратный корень из
известного значения:
a=√S
где S — площадь.
Цифр после
запятой:
Результат в:
Это самый простой способ. Площадь плоской четырёхугольной геометрической фигуры – это числовое
значение, которое характеризует размер плоскости, ограниченной четырьмя сторонами. Для нахождения
площади прямоугольника необходимо умножить длину на ширину, для площади прямоугольника с равными
сторонами – возвести длину в квадрат.
Также есть и другие способы для нахождения площади правильной
четырёхугольной фигуры: через радиус вписанной или описанной окружности, периметр, через длину
отрезка, проведенного из вершины к середине противоположной стороны. Если площадь неизвестна, но
есть данные о диагонали, можно легко найти воспользоваться доступной величиной — возвести
длину отрезка в квадрат и разделить на два S=d²/2.
Этот метод также
опирается на теорему Пифагора. Поделив сумму квадратов катетов на два, можно найти площадь. Однако в
этом случае значение не понадобится для нахождения стороны, можно быстро вычислить длину катета при
помощи следующей формулы.
Вычисление через диагональ
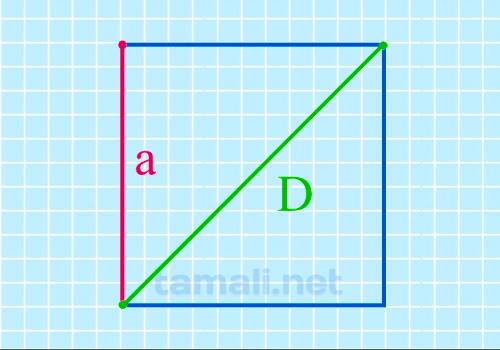
Если в задаче изначально известна длина диагонали, можно значительно сократить маршрут поиска нужной
величины. На основе этого правила сторона вычисляется по формуле:
a=d/√2
где d — диагональ.
Цифр после
запятой:
Результат в:
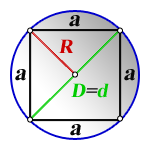
Через радиус описанной окружности
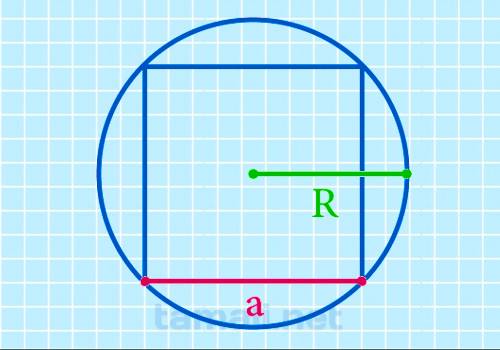
Известно, что диаметр описанной окружности равен диагонали, так как он совпадает с отрезком,
соединяющим вершины двух противоположных углов, а эти вершины являются точками окружности. Формула
для вычисления:
a = √2 * R
где R — радиус.
Цифр после
запятой:
Результат в:
Благодаря радиусу можно найти длину диагонали, которая делит фигуру на 2 прямоугольных равнобедренных
треугольника и при помощи теоремы Пифагора найти нужную величину.
Диагональ представляет собой линию, которая соединяет две вершины противоположных углов, тем самым
разделяя правильный четырёхугольник на два равнобедренных прямоугольных треугольника. Найти значение
таким способом не сложнее, чем через площадь. Главное, знать теорему Пифагора и уметь ею
пользоваться, это самый быстрый вариант. В задачах с прямоугольными фигурами теорема часто служит
выходом из сложной ситуации.
Все вычислительные способы связаны между собой. Запомнить нужные формулы несложно. Достаточно
применять их на практике каждый день, частое использование одних и тех же алгоритмов приведет к
автоматическому запоминаю правил. Не стоит заучивать формулы, необходимо больше рассуждать
логически. Такой подход позволит решать задачи более сложного уровня и легче воспринимать любую
информацию. Самым действенным методом для запоминания является практика. Отработка нескольких
идентичных задач на определенное правило поможет закрепить результат на долгий срок.
1. Формула стороны квадрата через диагональ
a – сторона квадрата
d – диагональ квадрата
Формула стороны квадрата, (a):
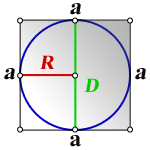
2. Формула стороны квадрата через радиус вписанной окружности
a – сторона квадрата
R – радиус вписанной окружности
D – диаметр вписанной окружности
Формула стороны квадрата, (a):
3. Формула стороны квадрата через радиус описанной окружности
a – сторона квадрата
R – радиус описанной окружности
D – диаметр описанной окружности
d – диагональ
Формула стороны квадрата, (a):
4. Формула стороны квадрата через площадь и периметр
a – сторона квадрата
S – площадь квадрата
P – периметр квадрата
Формула стороны квадрата, (a):
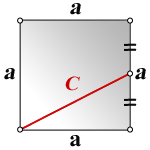
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a – сторона квадрата
C – линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
- Подробности
-
Опубликовано: 13 октября 2013
-
Обновлено: 13 августа 2021
Расчет площади геометрических фигур — это базовый навык, необходимый в математике, инженерии, архитектуре и других науках. Однако, на практике возникает необходимость не только вычислять площадь фигуры, но и находить зависимости, например, между площадью и другими характеристиками фигуры. В этой статье мы поможем вам разобраться в том, как с помощью известной площади определить стороны простых фигур, таких как треугольник, прямоугольник и круг.
Определение сторон фигуры по площади может оказаться сложным для новичков. Если вы сталкивались с трудностями в подобных расчетах, то наш гайд будет очень полезен для вас. В этой статье мы рассмотрим несколько методов расчета, которые помогут вам быстро и точно найти значения сторон фигуры по известной площади.
Мы рекомендуем обратить внимание на примеры расчета, чтобы лучше понять, как выполнить расчет сторон фигуры по известной площади. Подобные расчеты важны не только в учебных целях, но и на практике – при проектировании домов, дизайне интерьера, разработке игр и многих других областях.
Расчет сторон по площади фигур
К слову, найти стороны по площади фигуры не такая уж и сложная задача! Сегодняшний гайд поможет вам быстро и правильно определить неизвестные стороны треугольника, квадрата, прямоугольника и круга.
Расчет сторон треугольника по заданной площади
Если известна площадь треугольника и одна из сторон, то оставшиеся стороны можно определить по формуле:
сторона_1 = 2 * площадь / сторона_2
сторона_3 = sqrt(сторона_2^2 — (4 * площадь^2) / сторона_2^2)
Расчет сторон квадрата и прямоугольника по заданной площади
Если известна площадь квадрата или прямоугольника, то стороны можно найти по следующим формулам:
- сторона_квадрата = sqrt(площадь)
- сторона_прямоугольника_1 = площадь / сторона_прямоугольника_2
- сторона_прямоугольника_2 = площадь / сторона_прямоугольника_1
Расчет радиуса круга по заданной площади
Если известна площадь круга, то радиус можно найти по формуле:
радиус = sqrt(площадь / pi)
Теперь вы знаете, как найти стороны по площади фигур различных форм и размеров. Так что не бойтесь экспериментировать и считать, ведь математика — это прекрасно!
Примеры простых фигур и способы их расчета
Квадрат
Квадрат — это фигура с четырьмя равными сторонами, значит, для расчета площади нужно умножить сторону на саму себя.
Формула: S=а²
Прямоугольник
Прямоугольник имеет две пары равных сторон, поэтому для расчета его площади нужно умножить длину на ширину.
Формула: S=а*b
Треугольник
Площадь треугольника можно расcчитать по формуле Герона или через высоту, проведенную к одной из сторон.
- Формула Герона: S=√(p*(p-a)*(p-b)*(p-c)), где p — полупериметр a, b, c — стороны
- Формула через высоту: S=0.5*a*h, где a — основание, h — высота, проведенная к этому основанию
Круг
Для расчета площади круга нужно умножить квадрат радиуса на число π
Формула: S=πr²
Трапеция
Площадь трапеции вычисляется по формуле, использующей среднюю линию и высоту.
Формула: S=0.5*(a+b)*h, где a и b — основания, h — высота
Как использовать формулы для расчета сложных фигур
Для расчета площади сложных фигур, необходимо использовать соответствующие формулы. Например, для расчета площади круга, используется формула S=πr², где S – площадь, π – число Пи, r – радиус круга. Для расчета площади треугольника, используется формула S=½ah, где a – длина основания, h – высота треугольника.
Если нужно посчитать площадь нестандартной фигуры, можно разбить ее на более простые части и посчитать их площадь отдельно. Например, для расчета площади трапеции, можно разбить ее на два треугольника и прямоугольник, а затем применить соответствующие формулы.
Помимо формул для расчета площади, существуют также формулы для расчета периметра и диаметра фигур. Знание данных формул поможет не только посчитать площадь, но и оценить длину границ фигуры и ее диаметр.
Важно помнить, что точность расчетов зависит от точности измерений сторон и углов фигуры. При неправильном измерении может получиться неверный результат при расчете площади.
- Пример
- Для расчета площади круга с радиусом 5 см, используем формулу S=πr². Решаем:
- π=3,14
- r=5
- S=3,14*5²=78,5 см²
Инструменты для быстрого и точного расчета площади
Для того чтобы быстро и точно рассчитать площадь фигуры, существует несколько инструментов:
- Калькулятор — позволяет быстро производить расчеты, сокращая время на примитивные операции.
- Геометрические фигуры — знание формул площади и периметра геометрических фигур позволяет быстро и точно расчитать площадь.
- Графический редактор — позволяет измерять площадь на изображении фигуры, возможность выделения определенных участков и расчета площади.
- Приборы точного замера расстояний — лазерный дальномер и металлический линейка позволяют с точностью до миллиметра провести замеры и рассчитать площадь.
Выбирайте инструмент, который подходит конкретно вам, учитывая характеристики фигуры и задачу, которую необходимо решить.
| Инструмент | Преимущества | Недостатки |
|---|---|---|
| Калькулятор | Быстрота расчетов | Не подходит для всех форм фигур |
| Геометрические фигуры | Высокая точность | Необходимо знание формул |
| Графический редактор | Возможность измерения на изображении | Требуется определенная программная поддержка |
| Приборы точного замера расстояний | Максимальная точность | Могут быть не удобны в использовании |
Учет нестандартных форм и неровностей в расчетах
При расчете площади фигур, основанных на нестандартных формах и неровностях, важно обратить внимание на каждый отдельный элемент. Например, при расчете площади комнаты с выступающей нишей необходимо учесть площадь и форму ниши и вычесть ее из общей площади.
О принципах расчета таких фигур нужно думать заранее, чтобы не допустить ошибок в расчетах и не потратить потом дополнительное время на их исправление.
Важно также обратить внимание на использование правильной единицы измерения. Например, при расчете площади комнаты, в которой высота потолков отличается в разных частях, необходимо использовать формулу площади треугольника, умноженную на высоту. В этом случае важно провести все расчеты в одинаковых единицах измерения.
- Для точности расчетов также необходимо учитывать неровности поверхности, на которой проводятся измерения. Например, в комнатах с неровными стенами или кривыми углами, нужно внести соответствующие корректировки в формулу расчета площади.
- Также можно использовать метод аппроксимации для определения площади нестандартных фигур. Данный метод позволяет приблизительно определить площадь, проводя замеры в нескольких ключевых точках фигуры и на основании полученных данных рассчитывать площадь.
Советы по сохранению точности в расчетах и избежанию ошибок
Используйте единицы измерения
Перед началом расчетов убедитесь, что вы используете правильные единицы измерения для каждого параметра. Например, если вы хотите вычислить площадь прямоугольника, то ширина и высота должны быть измерены в одной и той же единице, например, в сантиметрах.
Проверяйте формулы
Перед тем, как начать расчеты, проверьте формулы. Возможно, вы уже знакомы с формулой для расчета площади круга, но неверно взяли значение радиуса. Внимательно проверьте каждый параметр и каждую формулу, чтобы избежать ошибок в расчетах.
Проверяйте свои вычисления
После того, как вы закончили все расчеты, проверьте свои вычисления, чтобы убедиться в их точности. Можете использовать калькулятор или другие инструменты, чтобы перепроверить свои результаты.
Если возникли сомнения, перепроверьте
Если вы не уверены в своих вычислениях, не стесняйтесь их перепроверить. Лучше потратить немного больше времени на тщательные расчеты, чем допустить ошибку, которая может привести к неправильным результатам. Если вы не можете понять, почему ваш результат неправильный, обратитесь за помощью к другим людям или используйте специальные программы для расчетов.
Не округляйте результаты до последней цифры
Всегда оставляйте некоторую запасную цифру, чтобы избежать закономерных ошибок округления. Например, если ваш результат 5,54567, то лучше округлить до двух знаков после запятой до 5,55, а не до 5,54. Это может избежать дополнительных ошибок в будущем.
Применение расчетов площади фигур в повседневной жизни
Расчет площади различных фигур может пригодиться в повседневной жизни. Например, при выборе покрытия для пола или стен необходимо рассчитать площадь помещения и приобрести нужное количество материала.
Также расчеты площади могут пригодиться при планировании мебели в комнате. Необходимо знать площадь комнаты, чтобы определить, сколько мебели будет в ней умещаться.
Расчеты площади фигур могут также пригодиться при проектировании сада или зеленых насаждений. Необходимо знать площадь участка, чтобы определить, сколько растений, травы и деревьев необходимо приобрести.
В области строительства расчеты площади могут пригодиться при проектировании зданий, дорог и мостов. Используя информацию о площади, можно рассчитать необходимое количество строительных материалов.
Расчитывать площади фигур можно с помощью математических формул или с использованием онлайн-калькуляторов.
Где d – диагональ квадрата.
Где S – площадь квадрата
Где r – радиус вписанной окружности
Где R – радиус описанной окружности
Где P – периметр квадрата.
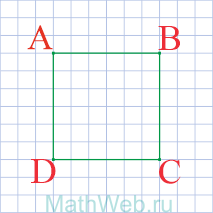
- Квадрат – это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные – перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
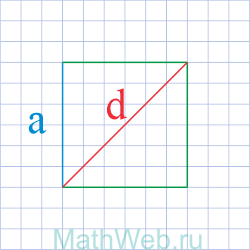
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = |
 |
a = √S |
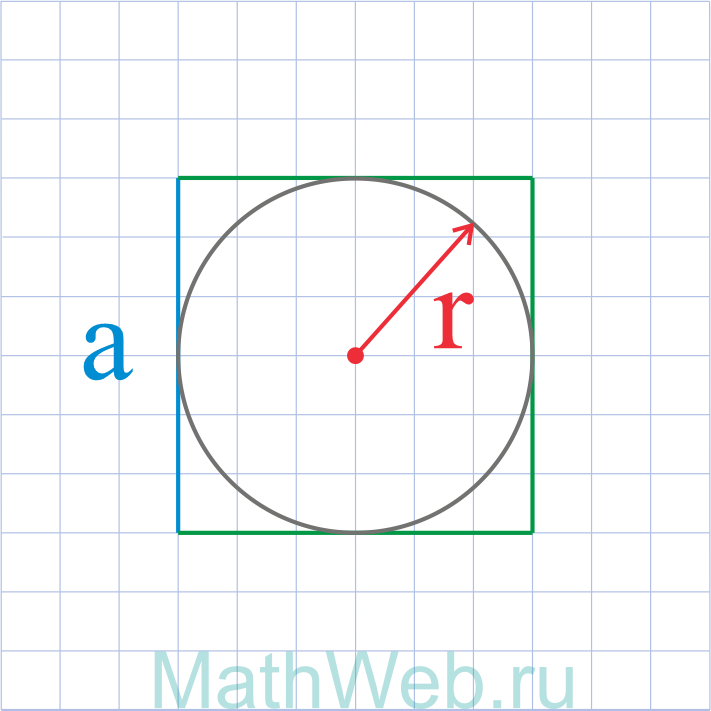 |
a = 2r |
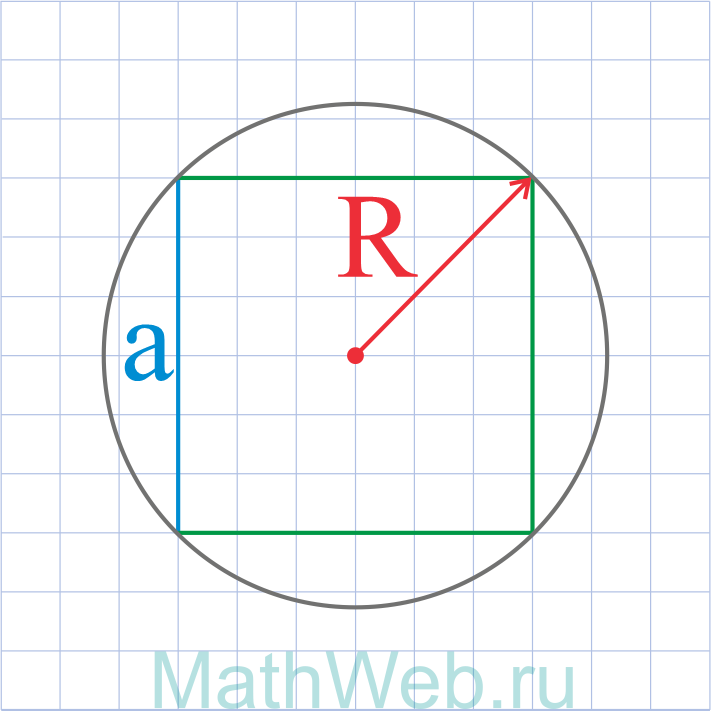 |
a = R√2 |
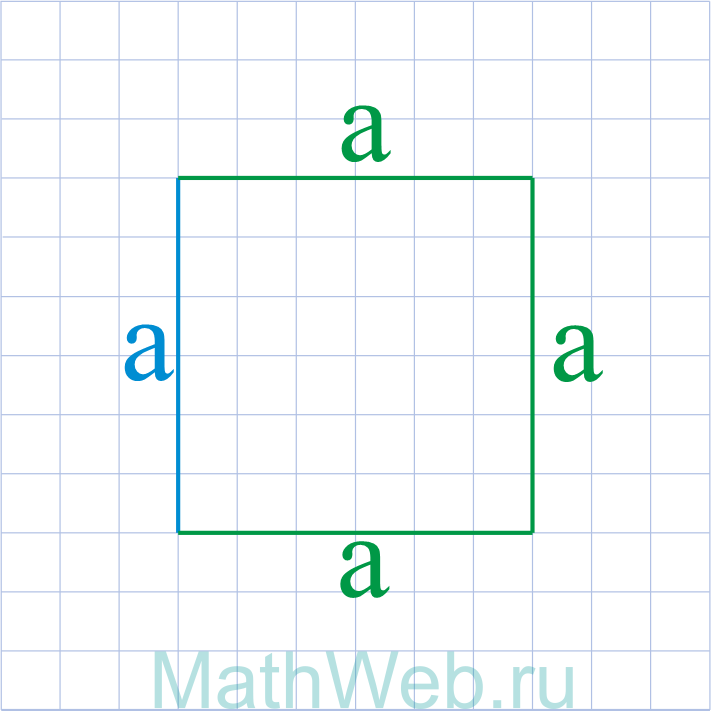 |
a = |
/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
527 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
824 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1023 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот