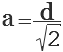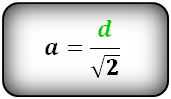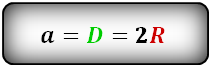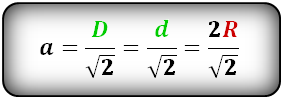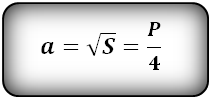Сторона квадрата
Стороны фигур
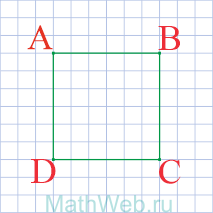
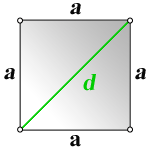
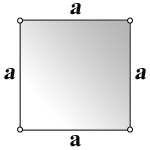
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d2 = а2 + а2 = 2а2.
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
Расчет стороны квадрата через диагональ
Расчет стороны квадрата через площадь
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):
Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:
Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a2+a2=d2
2a2=d2
Как найти сторону квадрата, зная его диагональ
Квадратом называют ромб с прямыми углами. Эта фигура одновременно является параллелограммом, прямоугольником и ромбом, обладая исключительными геометрическими свойствами. Найти сторону квадрата через его диагональ можно несколькими способами.
Поскольку удиагонали равны между собой (это свойство ему досталось «по наследству» от прямоугольника), то для того, чтобы найти сторону квадрата достаточно знать длину одной диагонали. Диагональ и две стороны квадрата, примыкающие к ней, представляют прямоугольный (поскольку все углы квадрата прямые) и равнобедренный (так как все стороны этой фигуры равны) треугольник. В этом треугольнике стороны квадрата являются катетами, а диагональ гипотенузой. Чтобы найти сторону квадрата, воспользуйтесь теоремой Пифагора.
Поскольку сумма квадратов катетов, которые равны a, равна квадрату гипотенузы, которую обозначьтеc (c²=a²+a²), то катет будет равен гипотенузе, поделенной на корень квадратный из числа 2, что проистекает и предыдущего выражения a=c/√2. Например, чтобы найти сторону квадрата с диагональю 12 см, это число поделите на корень квадратный из 2. Получите a=12/√2≈8,5 см. С учетом того, что корень квадратный из 2 нацело не извлекается, все ответы придется округлять с нужной точностью.
Сторону квадрата найдите, используя соотношение углов и сторон в прямоугольном треугольнике, который образуется диагональю и примыкающими к ней сторонами. Известно, что один из углов этого треугольника прямой (как угол между сторонами квадрата), а два других равны между собой и составляют 45º. Это свойство проистекает из равнобедренности этого треугольника, поскольку катеты его равны между собой.
Чтобы найти сторону квадрата, умножьте диагональ на синус или косинус угла 45º (они равны между собой, как прилежащий и противолежащий катеты sin(45º)=cos(45º)=√2/2) a=c∙√2/2. Например, дана диагональ квадрата, равная 20 см, нужно найти его сторону. Произведите расчет согласно указанной выше формуле, результатом будет сторона квадрата с нужной степенью точностиa=20∙√2/2≈14,142 см.
Где d – диагональ квадрата.
Где S – площадь квадрата
Где r – радиус вписанной окружности
Где R – радиус описанной окружности
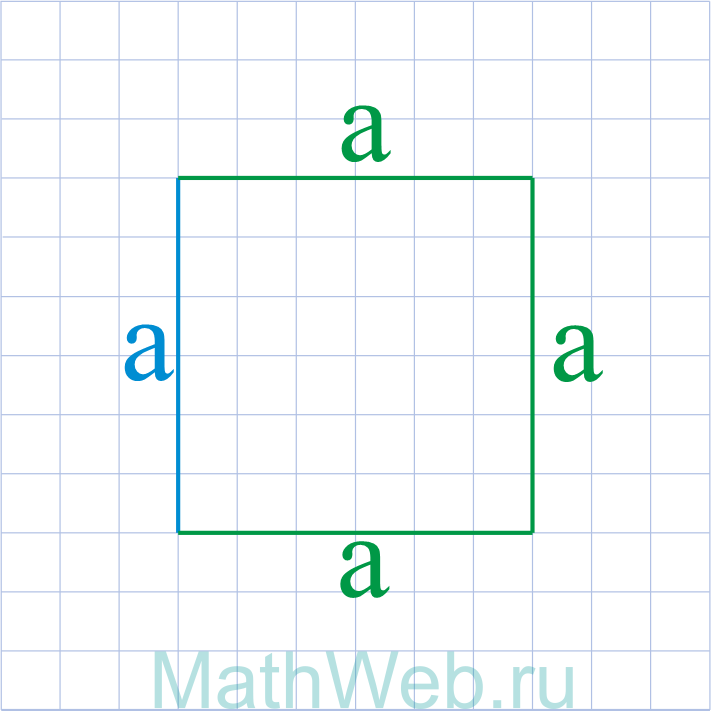
Где P – периметр квадрата.
- Квадрат – это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные – перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = |
 |
a = √S |
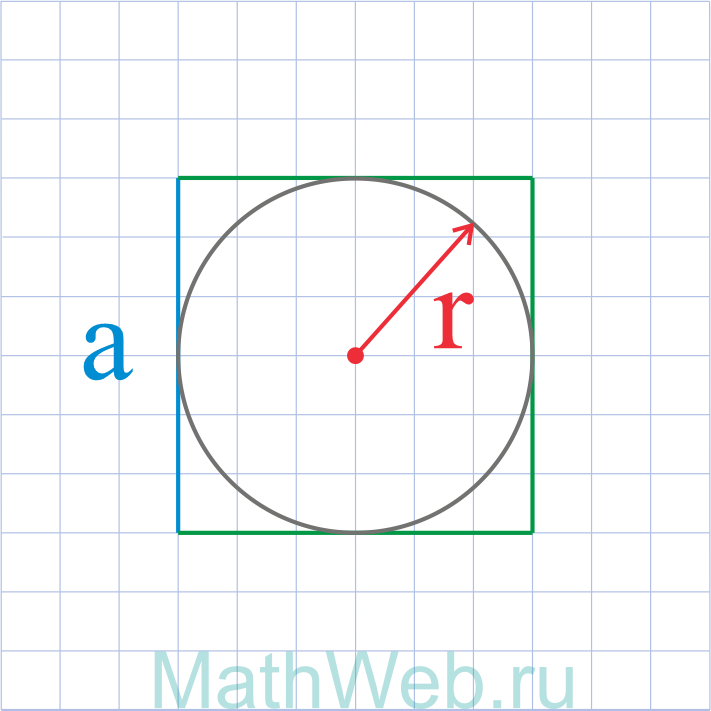 |
a = 2r |
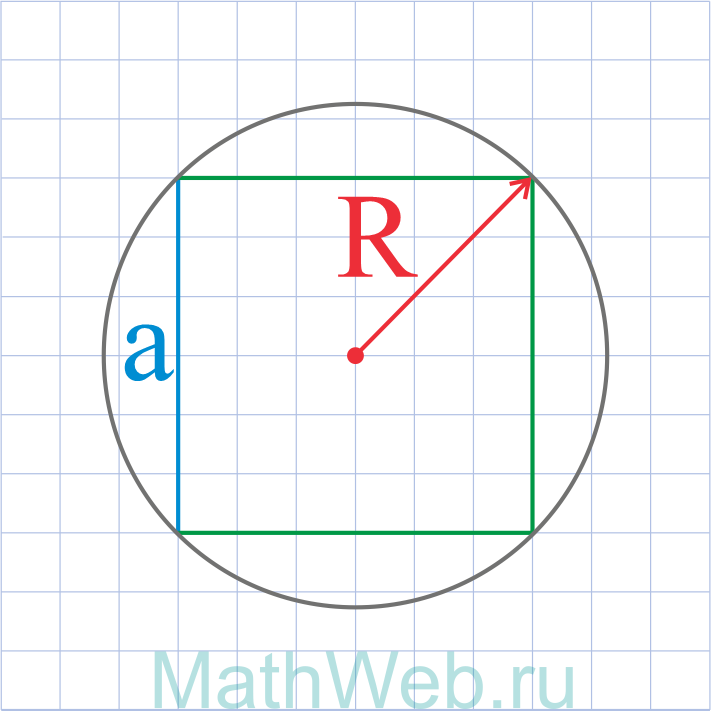 |
a = R√2 |
 |
a = |
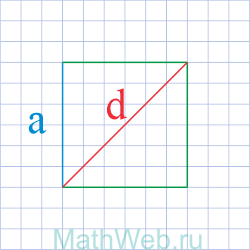
1. Формула стороны квадрата через диагональ
a – сторона квадрата
d – диагональ квадрата
Формула стороны квадрата, (a):
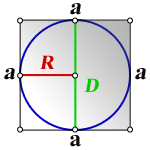
2. Формула стороны квадрата через радиус вписанной окружности
a – сторона квадрата
R – радиус вписанной окружности
D – диаметр вписанной окружности
Формула стороны квадрата, (a):
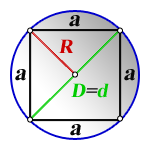
3. Формула стороны квадрата через радиус описанной окружности
a – сторона квадрата
R – радиус описанной окружности
D – диаметр описанной окружности
d – диагональ
Формула стороны квадрата, (a):
4. Формула стороны квадрата через площадь и периметр
a – сторона квадрата
S – площадь квадрата
P – периметр квадрата
Формула стороны квадрата, (a):
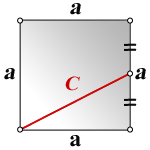
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a – сторона квадрата
C – линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
- Подробности
-
Опубликовано: 13 октября 2013
-
Обновлено: 13 августа 2021