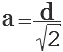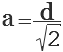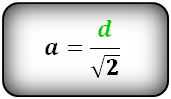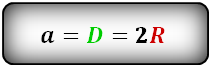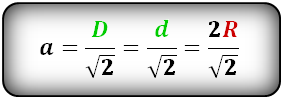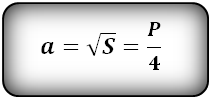как найти сторону квадрата если известна только площадь?!
Ученик
(107),
закрыт
6 лет назад
Quantorus3d
Знаток
(277)
6 лет назад
Площадь на 4 делить не надо!!!!
А как найти ответы я не знаю.
Вот задача
Площадь участка равна 100м кв. Чему равна сторона.
Прошу! Без корня я ещё не знаю этого.
LK ОМСК-СТРОЙ
Ученик
(158)
6 лет назад
Как найти сторону квадрата если известна только площадь. Площадь делить на 2 и 4 нельзя так мы не узнаем его стороны. Единственно верный вариант это найти квадратный корень, но это 4 класс они этого ещё не проходят.
елена сисецкая
Профи
(546)
6 лет назад
В этом случае нужно подобрать два одинаковых числа произведение которых равнялось бы числу, обозначающему площадь квадрата. (другими словами, найти квадратный корень числа, обозначающего площадь квадрата) Формула площади квадрата S = а * а или S = а², значит, чтобы найти сторону нужно извлечь корень из площади а = √
ODuHOKuu_BOJIK
Мастер
(1507)
5 лет назад
Извлечь квадратный корень, если корни не проходили, то нужно найти с начало периметр S:4=P. А т. к. у квадрата все стороны равны, то P:4=x – это и есть сторона квадрата.
S – площадь
P – периметр
x – сторона квадрата
/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
523 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
820 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1019 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот
Где d – диагональ квадрата.
Где S – площадь квадрата
Где r – радиус вписанной окружности
Где R – радиус описанной окружности
Где P – периметр квадрата.
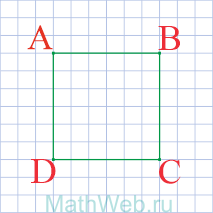
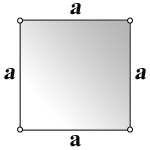
- Квадрат – это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные – перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
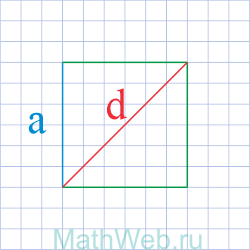 |
a = |
 |
a = √S |
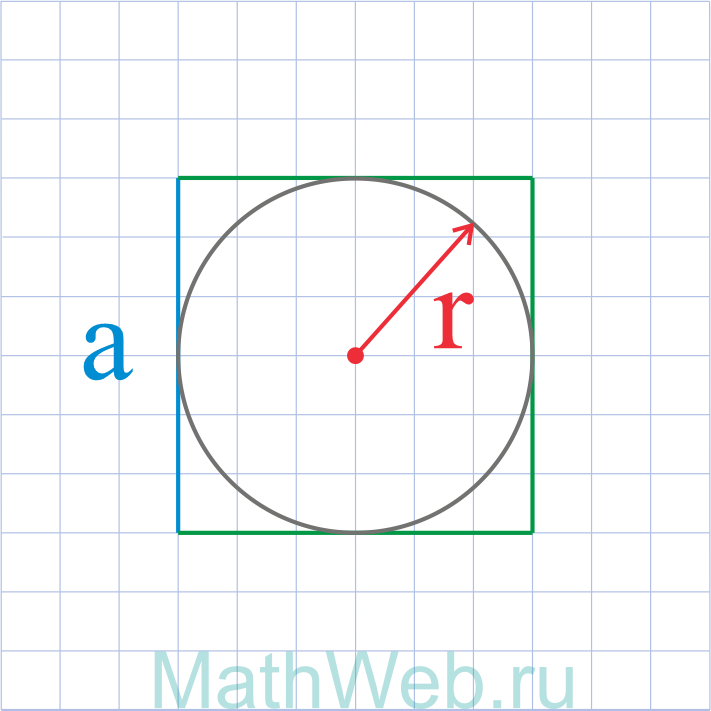 |
a = 2r |
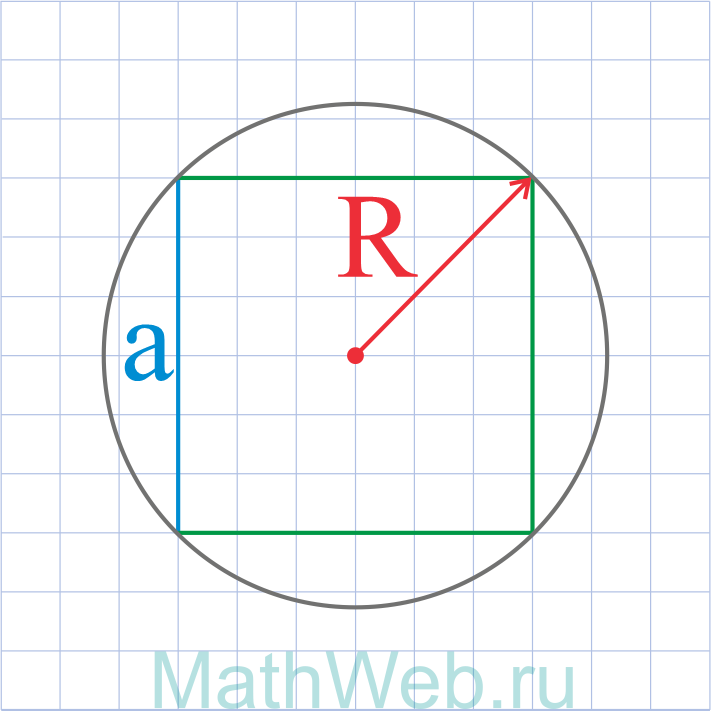 |
a = R√2 |
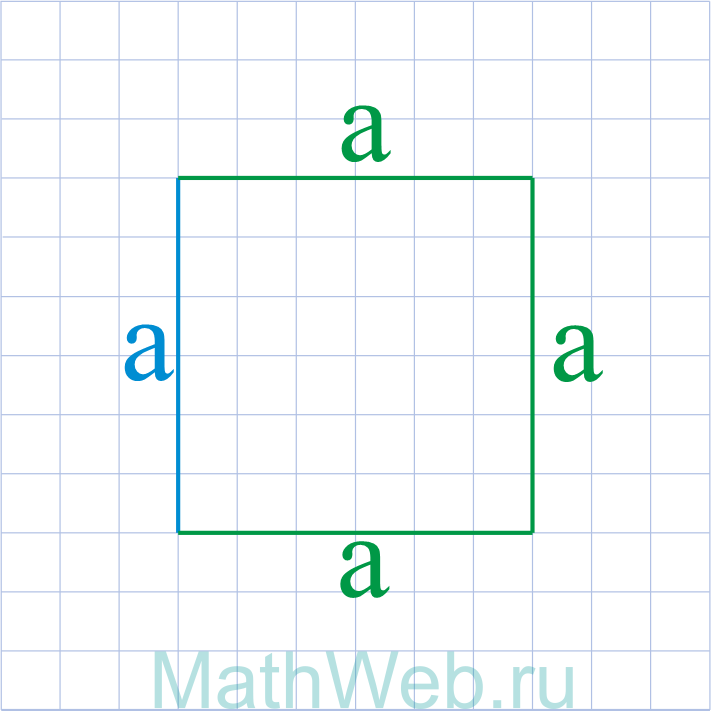 |
a = |
Как найти сторону квадрата?
Часто в геометрии необходимо найти длину стороны квадрата, при этом известны такие его параметры: периметр, площадь, длина диагонали.
Квадрат — это ромб или прямоугольник, стороны которого равны между собой. Углы квадрата также равны между собой и имеют по 90° каждый. Рассмотрим, как найти сторону квадрата имея один из вышеперечисленных параметров.
Нахождение стороны квадрата по его периметру
В этом случае, чтобы найти длину стороны квадрата, необходимо число значения периметра квадрата разделить на 4 (поскольку квадрат имеет 4 стороны, равные между собой): z = P/4, где z — это длина стороны квадрата; P — это периметр квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его периметра. Например, если задан периметр квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.
Например: Задан периметр квадрата 40 метров. При решении этой задачи мы получим: z = 40/4 = 10. Длина стороны квадрата — 10 метров.
Нахождение стороны квадрата по его площади
В этом случае, чтобы найти длину стороны, необходимо добыть квадратный корень числа значения площади (поскольку площадь квадрата равна квадрату его стороны): z = vS, где z — это длина стороны квадрата; S — это площадь квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его площади. Например, если задана площадь квадрата в миллиметрах квадратных — длина его стороны будет просто в миллиметрах.
Например: Задана площадь квадрата 16 квадратных метров. При решении этой задачи мы получим: z = v9 = 3. Длина стороны квадрата — 4 метра.
Нахождение стороны квадрата по его диагонали
В этом случае длина стороны квадрата будет равна длине диагонали квадрата, разделенной на корень квадратный из 2 (за теоремой Пифагора, поскольку смежные стороны квадрата и его диагональ составляют равнобедренный прямоугольный треугольник). Чтобы найти сторону квадрата по диагонали необходимо: z = d/v2 (так как z 2 + z 2 = d 2 ), где: z — это длина стороны квадрата; d — это длина диагонали квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его диагонали. Например, если задана диагональ квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.
Например: Задана диагональ квадрата 20 метров. При решении этой задачи мы получим: z = 20/v2, это приблизительно равно 20/1,4142. Длина стороны квадрата — 20/v2 метров, или, приблизительно, 14,142 метров.
Теперь Вы знаете, как найти длину стороны квадрата, если заданы его периметр, площадь или длина диагонали.
Сторона квадрата
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):
Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:
Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a 2 +a 2 =d 2
2a 2 =d 2
Сторона квадрата
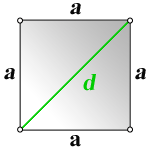
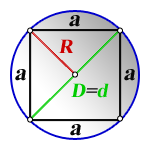
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d 2 = а 2 + а 2 = 2а 2 .
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
1. Формула стороны квадрата через диагональ
a – сторона квадрата
d – диагональ квадрата
Формула стороны квадрата, (a):
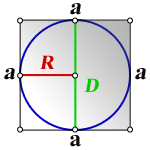
2. Формула стороны квадрата через радиус вписанной окружности
a – сторона квадрата
R – радиус вписанной окружности
D – диаметр вписанной окружности
Формула стороны квадрата, (a):
3. Формула стороны квадрата через радиус описанной окружности
a – сторона квадрата
R – радиус описанной окружности
D – диаметр описанной окружности
d – диагональ
Формула стороны квадрата, (a):
4. Формула стороны квадрата через площадь и периметр
a – сторона квадрата
S – площадь квадрата
P – периметр квадрата
Формула стороны квадрата, (a):
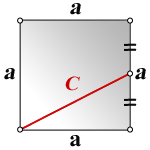
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a – сторона квадрата
C – линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
- Подробности
-
Опубликовано: 13 октября 2013
-
Обновлено: 13 августа 2021