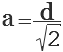Как найти сторону квадрата?
Часто в геометрии необходимо найти длину стороны квадрата, при этом известны такие его параметры: периметр, площадь, длина диагонали.
Квадрат — это ромб или прямоугольник, стороны которого равны между собой. Углы квадрата также равны между собой и имеют по 90° каждый. Рассмотрим, как найти сторону квадрата имея один из вышеперечисленных параметров.
Нахождение стороны квадрата по его периметру
В этом случае, чтобы найти длину стороны квадрата, необходимо число значения периметра квадрата разделить на 4 (поскольку квадрат имеет 4 стороны, равные между собой): z = P/4, где z — это длина стороны квадрата; P — это периметр квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его периметра. Например, если задан периметр квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.
Например: Задан периметр квадрата 40 метров. При решении этой задачи мы получим: z = 40/4 = 10. Длина стороны квадрата — 10 метров.
Нахождение стороны квадрата по его площади
В этом случае, чтобы найти длину стороны, необходимо добыть квадратный корень числа значения площади (поскольку площадь квадрата равна квадрату его стороны): z = vS, где z — это длина стороны квадрата; S — это площадь квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его площади. Например, если задана площадь квадрата в миллиметрах квадратных — длина его стороны будет просто в миллиметрах.
Например: Задана площадь квадрата 16 квадратных метров. При решении этой задачи мы получим: z = v9 = 3. Длина стороны квадрата — 4 метра.
Нахождение стороны квадрата по его диагонали
В этом случае длина стороны квадрата будет равна длине диагонали квадрата, разделенной на корень квадратный из 2 (за теоремой Пифагора, поскольку смежные стороны квадрата и его диагональ составляют равнобедренный прямоугольный треугольник). Чтобы найти сторону квадрата по диагонали необходимо: z = d/v2 (так как z 2 + z 2 = d 2 ), где: z — это длина стороны квадрата; d — это длина диагонали квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его диагонали. Например, если задана диагональ квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.
Например: Задана диагональ квадрата 20 метров. При решении этой задачи мы получим: z = 20/v2, это приблизительно равно 20/1,4142. Длина стороны квадрата — 20/v2 метров, или, приблизительно, 14,142 метров.
Теперь Вы знаете, как найти длину стороны квадрата, если заданы его периметр, площадь или длина диагонали.
Сторона квадрата
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):
Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:
Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a 2 +a 2 =d 2
2a 2 =d 2
Сторона квадрата
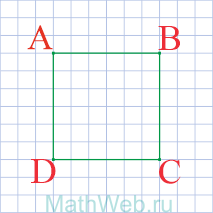
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d 2 = а 2 + а 2 = 2а 2 .
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
Где d – диагональ квадрата.
Где S – площадь квадрата
Где r – радиус вписанной окружности
Где R – радиус описанной окружности
Где P – периметр квадрата.
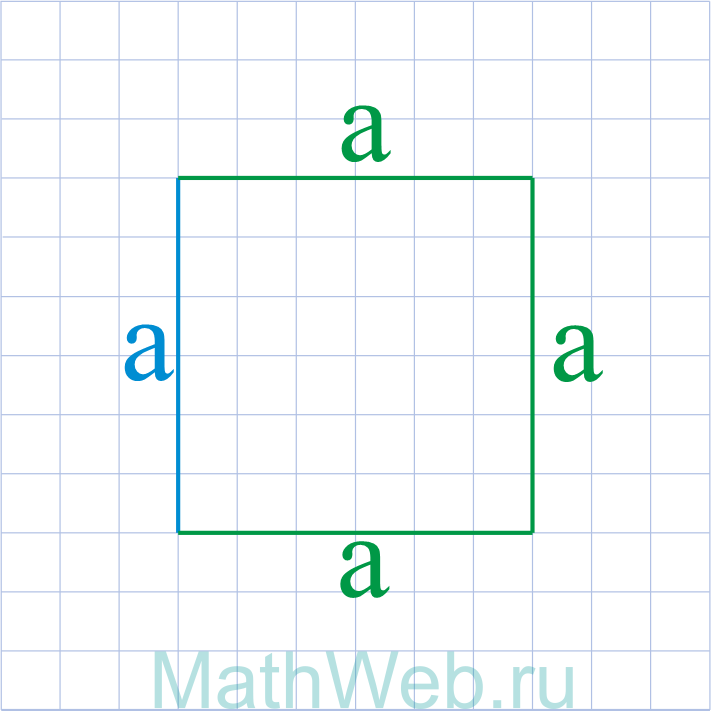
- Квадрат – это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные – перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
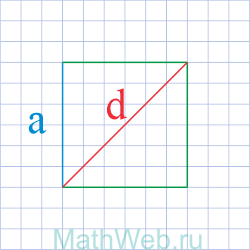 |
a = |
 |
a = √S |
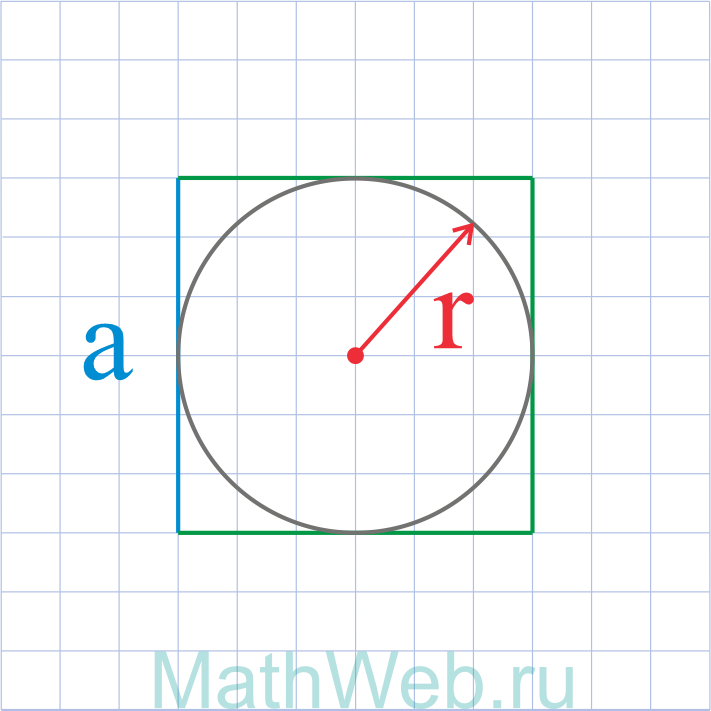 |
a = 2r |
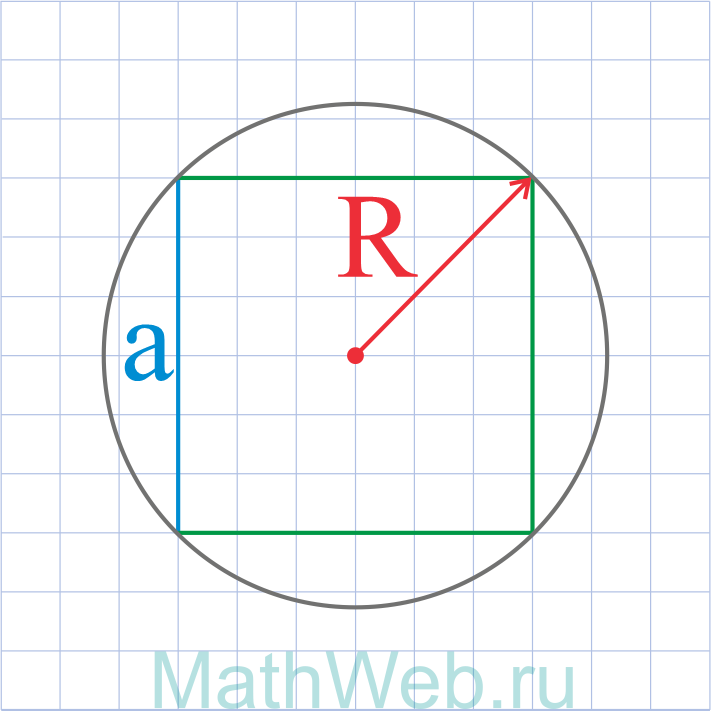 |
a = R√2 |
 |
a = |
Как найти сторону квадрата из площади через периметр?
без использования квадратного корня и возведения во вторую степень
Управление о.
12 декабря 2018 · 20,2 K
Допустим, сторона квадрата это a, периметр квадрата это P, площадь квадрата это S. Простые формулы периметра и площади таковы: P=4*a и S=a*a
Выделим сторону a из каждой формулы, получаем a=P/4 и a=S/a
Стороны равны, поэтому P/4=S/a
Отсюда P*a=4*S
Отсюда a=4*S/P
13,4 K
Комментировать ответ…Комментировать…
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Площадь (S) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{S}) = (sqrt{10}) = 3.16
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*3.16^{2}}) = 4.47
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{3.16}{2}) = 1.58
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{4.47}{2}) = 2.24
Периметр (P) = (L*4) = (3.16*4) = 12.64