Как найти сторону на которую опустили биссектрису – Сайт, где вы сможете решить свои вопросы

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

Как найти неизвестную сторону треугольника

a, b, c – стороны произвольного треугольника

α, β, γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), (a):

Формула стороны треугольника по теореме косинусов

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), (a):

Формула стороны по теореме синусов

Есть следующие формулы для определения катета или гипотенузы

Формулы для прямоугольного треугольника

a, b – катеты

c – гипотенуза

α, β – острые углы

Формулы для катета, (a):

Формулы катета прямоугольного треугольника

Формулы для катета, (b):

Формулы катета прямоугольного треугольника

Формулы для гипотенузы, (c):

Формулы гипотенузы прямоугольного треугольника

формула гипотенузы прямоугольного треугольника

Формулы сторон по теореме Пифагора, (a,b):

Формула стороны по теореме Пифагора

Вычислить длину неизвестной стороны через любые стороны и углы

Формулы сторон равнобедренного треугольника

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b):

Формулы длины равных сторон , (a):

Формулы длины равных сторон

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

Найти длину высоты треугольника H – высота треугольника

a – сторона, основание

b, c – стороны

β, γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, (H):

Формула длины высоты через стороны

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и угол

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через сторону и площадь

Формула длины высоты через стороны и радиус, (H):

Формула длины высоты через стороны и радиус

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

Формулы высоты прямого угла в прямоугольном треугольнике
H – высота из прямого угла

a, b – катеты

с – гипотенуза

c₁, c₂ – отрезки полученные от деления гипотенузы, высотой

α, β – углы при гипотенузе

Формула длины высоты через стороны, (H):

Формула длины высоты через стороны

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через гипотенузу и острые углы

Формула длины высоты через катет и угол, (H):

Формула длины высоты через катет и угол

Формула длины высоты через составные отрезки гипотенузы , (H):

Формула длины высоты через составные отрезки гипотенузы

Найти длину биссектрисы в треугольнике

L– биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b – стороны треугольника

с – сторона на которую опущена биссектриса

d, e – отрезки полученные делением биссектрисы

γ – угол ABC , разделенный биссектрисой пополам

p – полупериметр, p=(a+b+c)/2

Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через две стороны и угол

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через полупериметр и стороны

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через три стороны

Длина биссектрисы через стороны и отрезки d, e, (L):

Длина биссектрисы через стороны и отрезки d, e

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

Биссектриса прямого угла прямоугольного треугольника

L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b – катеты прямоугольного треугольника

с – гипотенуза

α – угол прилежащий к гипотенузе

Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через катеты

Формула длины биссектрисы через гипотенузу и угол, ( L):

Формула длины биссектрисы через гипотенузу и угол

2. Найти по формулам длину биссектрисы из острого угла на катет:

Биссектриса из острого угла прямоугольного треугольника

L – биссектриса, отрезок ME , исходящий из острого угла

a, b – катеты прямоугольного треугольника

с – гипотенуза

α, β – углы прилежащие к гипотенузе

Формулы длины биссектрисы через катет и угол, (L):

Формула биссектрисы из острого угла прямоугольного треугольника через катет и угол

Формула длины биссектрисы через катет и гипотенузу, (L):

Формула биссектрисы из острого угла прямоугольного треугольника через катет и гипотенузу

Длина биссектрисы равнобедренного треугольника

L – высота = биссектриса = медиана

a – одинаковые стороны треугольника

b – основание

α – равные углы при основании

β – угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

Формулы высоты, биссектрисы и медианы равнобедренного треугольника

Формула высоты, биссектрисы и медианы, через стороны, (L):

Формулы высоты, биссектрисы и медианы равнобедренного треугольника

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

Найти медиану биссектрису высоту равностороннего треугольника

L – высота=биссектриса=медиана

a – сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Формула длины высоты, биссектрисы и медианы равностороннего треугольника

Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

Найти длину медианы треугольника по формулам

M – медиана, отрезок |AO|

c – сторона на которую ложится медиана

a, b – стороны треугольника

γ – угол CAB

Формула длины медианы через три стороны, (M):

Формула длины медианы через три стороны

Формула длины медианы через две стороны и угол между ними, (M):

Формула длины медианы через две стороны и угол между ними

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.

Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

Длина медианы прямоугольного треугольника

M – медиана

R – радиус описанной окружности

O – центр описанной окружности

с – гипотенуза

a, b – катеты

α – острый угол CAB

Медиана равна радиусу и половине гипотенузы, (M):

Медиана равна радиусу и половине гипотенузы

Формула длины через катеты, (M):

Формула медианы через катеты

Формула длины через катет и острый угол, (M):

Формула медианы через катет и острый угол

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 августа 2022 года; проверки требует 1 правка.

${displaystyle {frac {BD}{CD}}={frac {AB}{AC}}.}$

Теорема о биссектрисе — классическая теорема геометрии треугольника.

Формулировка[править | править код]

Биссектриса при вершине треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.
То есть, если биссектриса при вершине $A$ треугольника $triangle ABC$ пересекает сторону $BC$ в точке $D$ то

${displaystyle {frac {DB}{DC}}={frac {AB}{AC}}.}$

Замечания[править | править код]

История[править | править код]

Теорема о биссектрисе формулируется в шестой книге «Начал Евклида» (предложение III)^[1], в частности, на греческом языке в византийском манускрипте^[2].
Ранняя цитата по Евклиду этой теоремы в русскоязычных источниках содержится в одном из первых русских учебников геометрии — рукописи начала XVII века «Синодальная №42» (книга 1, часть 2, глава 21).

Доказательства[править | править код]

Существует несколько методов доказательства. Например, методом площадей или проведением из другой вершины прямой, параллельной биссектрисе, до ее пересечения с продолжением одной из сторон.

Метод площадей[править | править код]

Рассмотрим треугольник ABC. Из вершины A на сторону BC опущена биссектриса AD. Найдем площади треугольников ABD и ACD:

${displaystyle {frac {S_{ABD}}{S_{ACD}}}={frac {{frac {1}{2}}ABcdot ADcdot sin alpha }{{frac {1}{2}}ACcdot ADcdot sin alpha }}={frac {AB}{AC}}.}$

С другой стороны,

${displaystyle {frac {S_{ABD}}{S_{ACD}}}={frac {{frac {1}{2}}BDcdot AH}{{frac {1}{2}}CDcdot AH}}={frac {BD}{CD}}.}$

Значит,

${displaystyle {frac {BD}{CD}}={frac {AB}{AC}}.}$

Через теорему синусов[править | править код]

Рассмотрим треугольник ABC с биссектрисой AD. Запишем теорему синусов для треугольников ABD и ACD:

Доказательство теоремы о биссектрисе с помощью теоремы синусов

${displaystyle {frac {AB}{sin gamma }}={frac {BD}{sin alpha }},quad (1)}$

${displaystyle {frac {AC}{sin(180^{circ }-gamma )}}={frac {CD}{sin alpha }}.}$

Но ${displaystyle sin(180^{circ }-gamma )=sin gamma ,}$ следовательно,

${displaystyle {frac {AC}{sin gamma }}={frac {CD}{sin alpha }}.quad (2)}$

Поделив равенство (1) на равенство (2), получим:

${displaystyle {frac {BD}{CD}}={frac {AB}{AC}}.}$

Через подобие треугольников[править | править код]

Данный способ доказательства основан на продлении биссектрисы до пересечения с ней перпендикуляра, опущенного на нее из одной из вершин.

Доказательство теоремы о биссектрисе через подобие треугольников

Рассмотрим треугольник ABC с биссектрисой AD. Опустим перпендикуляры BK и CT на нее и ее продолжение соответственно. Треугольники KBD и TCD подобны по двум углам, значит,

${displaystyle {frac {BD}{CD}}={frac {BK}{CT}}.}$

Треугольники ABK и ACT тоже подобны по двум углам, значит, справедливо равенство:

${displaystyle {frac {AB}{AC}}={frac {BK}{CT}}.}$

Отсюда получаем, что ${displaystyle {frac {BD}{CD}}={frac {AB}{AC}}.}$

Вариации и обобщения[править | править код]

Биссекторная плоскость двугранного угла в тетраэдре (то есть плоскость, делящая двугранный угол пополам) делит противоположное его ребро на части, пропорциональные площадям граней тетраэдра, являющихся гранями этого двугранного угла^[3]^:200.

Теорема Штейнера.

См. также[править | править код]

Антибиссектриса
Биссектриса
Высота (геометрия)
Высота треугольника
Инцентр
Медиана треугольника
Симедиана
Ось внешних биссектрис или антиортовая ось
Треугольник
Треугольник трёх внешних биссектрис
Ось внешних биссектрис или антиортовая ось
Центроид
Чевиана

Примечания[править | править код]

↑ Эвклидовых начал восемь книг, а именно: первые шесть, 11-я и 12-я, содержащие в себе основания геометрии. / Пер. Ф. Петрушевского. — СПб., 1819. — С. 205. — 480 с. Архивная копия от 10 июля 2020 на Wayback Machine
↑ Теорема о биссектрисе в византийском манускрипте. Дата обращения: 24 мая 2012. Архивировано 26 мая 2012 года.
↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с. Архивная копия от 10 января 2014 на Wayback Machine

Литература[править | править код]

Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 18-19.

Источник

Все формулы биссектрисы в треугольнике

L – биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b – стороны треугольника

с – сторона на которую опущена биссектриса

d, e – отрезки полученные делением биссектрисы

γ – угол ABC , разделенный биссектрисой пополам

p – полупериметр, p =(a+b+ c )/2

Длина биссектрисы через две стороны и угол, ( L ):

Длина биссектрисы через полупериметр и стороны, ( L ):

Длина биссектрисы через три стороны, ( L ):

Длина биссектрисы через стороны и отрезки d , e , ( L ):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Длина биссектрисы треугольника

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Дано:

СF — биссектриса ∠ABC

Доказательство:

Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Что и требовалось доказать.

II. Через три стороны треугольника

Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

По свойству биссектрисы треугольника:

Согласно утверждению 1,

Что и требовалось доказать.

III Через две стороны треугольника и угол между ними.

Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле

[spoiler title=”источники:”]

Элементы треугольника. Биссектриса

Длина биссектрисы треугольника

[/spoiler]

Источник

Теорема о биссектрисе треугольника. Доказательство

Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:

Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:

Построим следующее соотношение

С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:

Построим следующее соотношение используя формулы (6) и (7):

Из формул (5) и (8) получим соотношение (1). Конец доказательства

Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).

Тогда площади треугольников ABD и ACD можно найти из формул:

Построим следующее соотношение

Из формул (5) и (11) получим соотношение (1). Конец доказательства

Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):

Применяя теорему синусов для треугольников ABD и ACD можем записать:

Поделив (12) на (13) и учитывая, что ( small sin(180°-delta)=sin delta , ) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1). Конец доказательства

Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.

Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (( small ∠ ALB= ∠ AKC ,;; ∠ BAL= ∠ CAK ) ). Тогда имеем:

Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку ( small ∠ BLD= ∠ CKD ,) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:

Из равенств (14) и (15) получаем:

Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.

Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:

Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:

или

Методом перекресного умножения упростим (17) и решим:

Тогда BD=x=15, CD=BC−x=20−x=5.

Ответ. BD=15, CD=5.

Источник

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Утверждение 1

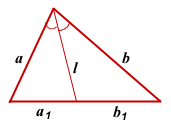
najti-dlinu-bissektrisy-treugolnika

$[ l = sqrt {ab - a_1 b_1 } ]$

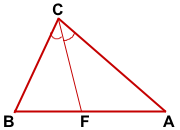dlina-bissektrisy Дано:

ΔABC,

СF — биссектриса ∠ABC

Доказать:

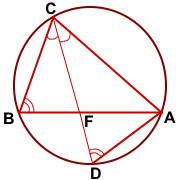dlina-bissektrisy-treugolnika Доказательство:

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

∠CBF=∠CDA (как вписанные углы, опирающиеся на одну дугу AC).

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$[ frac{{BC}}{{CD}} = frac{{CF}}{{AC}}, Rightarrow CD = frac{{BC cdot AC}}{{CF}}. ]$

$[ FD = CD - CF = frac{{BC cdot AC}}{{CF}} - CF. ]$

По свойству пересекающихся хорд

Отсюда

$[ BF cdot AF = CF cdot (frac{{BC cdot AC}}{{CF}} - CF) ]$

Что и требовалось доказать.

II. Через три стороны треугольника

Утверждение 2

Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

$[ l_c = frac{1}{{a + b}}sqrt {ab(a + b + c)(a + b - c)} . ]$

Доказательство:

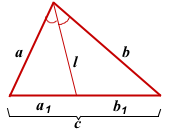dlina-bissektrisy-cherez-storony По свойству биссектрисы треугольника:

$[ [ frac{a}{{a_1 }} = frac{b}{{b_1 }}, Rightarrow a_1 b = ab_1 . ]$

a₁+b₁=c, b₁=c-a₁, поэтому

$[ a_1 = frac{{ac}}{{a + b}}. ]$

Согласно утверждению 1,

$[ l^2 = ab - a_1 (c - a_1 ) = ab - frac{{ac}}{{a + b}}(c - frac{{ac}}{{a + b}}) = ]$

$[ = ab - frac{{ac^2 }}{{a + b}} + frac{{a^2 c^2 }}{{(a + b)^2 }} = frac{{ab(a + b)^2 - ac^2 (a + b) + a^2 c^2 }}{{(a + b)^2 }} = ]$

$[ = frac{{ab(a + b)^2 - a^2 c^2 - abc^2 + a^2 c^2 }}{{(a + b)^2 }} = frac{{ab(a + b)^2 - abc^2 }}{{(a + b)^2 }} = ]$

$[ = frac{{ab}}{{(a + b)^2 }}((a + b)^2 - c^2 ) = frac{{ab}}{{(a + b)^2 }}((a + b) + c)((a + b) - c) = ]$

$[ = frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c), ]$

откуда

$[ l = sqrt {frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c)} , ]$

$[ l_c = frac{1}{{a + b}}sqrt {ab(a + b + c)(a + b - c)} . ]$

Что и требовалось доказать.

Аналогично,

$[ l_a = frac{1}{{b + c}}sqrt {bc(b + c + a)(b + c - a)} , ]$

$[ l_b = frac{1}{{a + c}}sqrt {ac(a + c + b)(a + c - b)} . ]$

III Через две стороны треугольника и угол между ними.

Утверждение 3

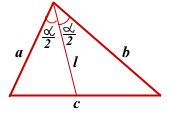
dlina-bissektrisy-cherez-storony-i-ugol

$[ l_c = frac{{2abcos frac{alpha }{2}}}{{a + b}} ]$

Доказательство:

Найдем площади треугольников BCF, ACF и ABC.

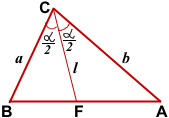
formula-dliny-bissektrisy

$[ S_{Delta BCF} = frac{1}{2}BC cdot CF cdot sin angle BCF, ]$

$[ S_{Delta ACF} = frac{1}{2}AC cdot CF cdot sin angle ACF, ]$

$[ S_{Delta ABC} = frac{1}{2}AC cdot BC cdot sin angle BCA. ]$

Так как

$[ S_{Delta ABC} = S_{Delta BCF} + S_{Delta ACF} , ]$

то

$[ frac{1}{2}AC cdot BC cdot sin angle BCA = ]$

$[ = frac{1}{2}BC cdot CF cdot sin angle BCF + frac{1}{2}AC cdot CF cdot sin angle ACF, ]$

$[ ab cdot sin alpha = al cdot sinfrac{alpha }{2} + bl cdot sinfrac{alpha }{2}, ]$

$[ ab cdot sin alpha = l cdot sinfrac{alpha }{2}(a + b), ]$

$[ l = frac{{ab cdot sin alpha }}{{sinfrac{alpha }{2}(a + b)}} = frac{{ab cdot sin (2 cdot frac{alpha }{2})}}{{sinfrac{alpha }{2}(a + b)}} = frac{{ab cdot 2sin frac{alpha }{2}cos frac{alpha }{2}}}{{sinfrac{alpha }{2}(a + b)}} = frac{{2abcos frac{alpha }{2}}}{{a + b}}. ]$

Что и требовалось доказать.

Источник

Формулировка[править | править код]

Замечания[править | править код]

История[править | править код]

Доказательства[править | править код]

Метод площадей[править | править код]

Через теорему синусов[править | править код]

Через подобие треугольников[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Все формулы биссектрисы в треугольнике

Элементы треугольника. Биссектриса

Свойства биссектрисы

Некоторые формулы, связанные с биссектрисой треугольника

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Длина биссектрисы треугольника

Теорема о биссектрисе треугольника. Доказательство

Вам также может понравиться

Как найти чудака в гта 5

Как найти собственника гаража заброшенного

Движение по наклонной плоскости как найти угол

Добавить комментарий Отменить ответ