Юлия Скаба
Знаток
(446),
на голосовании
10 лет назад
А полная поверхность прямоугольного параллел. (основание квадрат) = 264 см^2.
Голосование за лучший ответ
Dark
Профи
(822)
10 лет назад
Не понял, что значит выражение в скобках. Если его не учитывать, то основание, умноженное на высоту дает площадь параллелепипеда. Следовательно 264 делим на 8, узнаем длинну стороны основания.
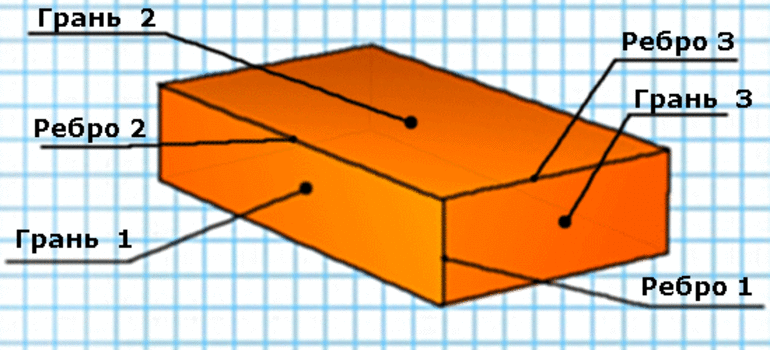
Общая характеристика
В мире имеется множество предметов с формой параллелепипеда. Люди обычно не задумываются об этом, но архитектура и различные массивные строения состоят из нескольких граней. Выглядеть параллелепипед может по-разному в зависимости от типа.
Основные понятия и классификация
Определение параллелепипеда, пирамиды, куба и других многогранников было известно с древнейших времен. Основными характеристиками являются простота и значимость.
Выведенные формулы V и S значимы для решения различных задач с практическим содержанием и доказательства теорем (по чертежам). Виды параллелепипеда:
- Прямой. Четыре боковые грани имеют углы по 90 градусов.
- Прямоугольный. Каждая сторона фигуры является прямоугольной.
- Наклонный.
- Двугранный, трехгранный. Состоит из нескольких граней под углом 90 градусов.
- Наклонный, диагональный. Боковые грани не перпендикулярны основаниям.
- Ромбоэдр. Стороны являются одинаковыми ромбами.
- Куб. Параллелепипед с равными (квадратными) сторонами.
В 6 классе на уроке геометрии изучают планиметрию (плоские фигуры). Здесь представлена развертка плоскостей.
Две стороны параллелепипеда, не имеющие общего ребра, называются противоположными, а содержащие единую линию — смежными. С точки зрения плоскостей, расположенных параллельно, внутри пересекаются три их пары. Эти вершины соединяет отрезок — диагональ. Длина трех ребер правильного многогранника называется измерением. Главным условием является общая вершина.
При решении задач важно понятие высоты — перпендикуляра, опущенного из любой вершины на обратную сторону. Грань, на которую опускается высота, считается основанием. Свойства параллелепипеда:
- любые стороны являются параллелограммами (с симметрией);
- стороны, расположенные друг против друга, будут параллельными и равными.
Кирпич — отличный пример прямоугольного параллелепипеда (ПП). Также его форму имеют девятиэтажные панельные дома, шифоньеры, шкафы-купе, контейнеры для хранения продуктов и прочие предметы быта.
Диагонали поверхности пересекаются и этой центральной точкой делятся на несколько частей. Они равны d2=a2+b2+c2
Грани параллелепипеда спереди и сзади равнозначны, также как верхняя и нижняя стороны, но не равны, поскольку не противоположные, а смежные.
Формулы и анализ
Для ПП верно мнение, что его объем равен величине тройного произведения векторов трех сторон, исходящих из единой вершины. Формулы для ПП:
- V=a*b*c.
- S б =2*c*(a+b).
- S п =2*(a*b+b*c+a*c).
Расшифровка обозначений: V — объем фигуры, S — площадь поверхности, a — длина, b — ширина, c — высота.
Особым случаем параллелепипеда, в котором все стороны квадраты, является куб. Если любую из сторон обозначить буквой a, то для поверхности и объема используются формулы: S=6*a*2, V=3*а. В них V — объем фигуры, a — длина грани.
Последняя разновидность параллелепипеда — прямой тип. Его основанием будет параллелограмм, а основанием ПП — прямоугольник. Формулы, используемые в математике и геометрии: Sб=Ро*h, Sп=Sб+2Sо, V=Sо*h.
Для нахождения ответов недостаточно знать только свойства геометрической фигуры. Могут пригодиться формулы для вычисления S и V.
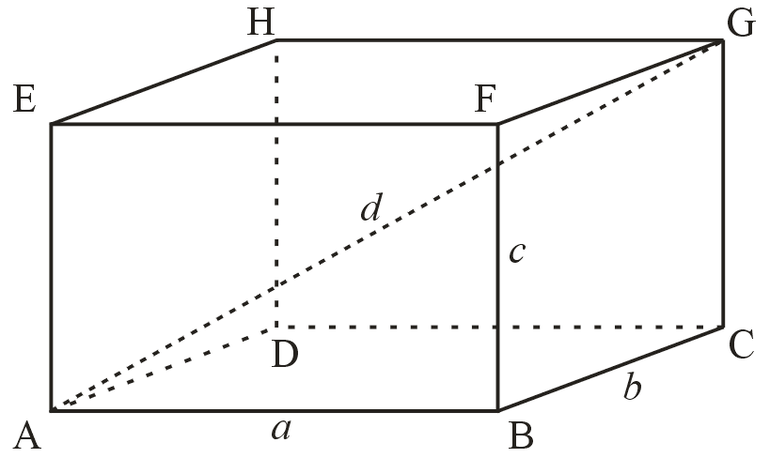
Диагональ ПП равна сложению квадратов его измерений: d2 = a2 + b2 + c2. Эта формула получается из теоремы Пифагора.
∆BAD — прямоугольный, поэтому BD2 = AB2 + AD2 = b2 + c2.
∆BDD1 является прямоугольным, значит, BD12 = BD2 + DD12. Нужно подставить значение: d2 = a2 + b2 + c2.
Стандартная формула: V= Sосн*h. Расшифровка обозначений: V — объем параллелепипеда, Sосн — площадь основания, h — высота.
S находится так же, как показатель параллелограмма или прямоугольника. При решении тестов и экзаменационных задач легче вычислять показатели призмы, в основе которой находится прямой угол. Также может пригодиться формула расчета стороны параллелепипеда Sбок = P*h, где:
- Sбок — площадь параллелепипеда;
- Р — периметр;
- h — высота, перпендикулярная основанию.
Объем фигуры равен величине смешанного произведения нескольких векторов, выпущенных из единой точки.
Практическое применение
Для вычисления объема, высоты и прочих характеристик фигуры нужно знать теоретические основы и формулы. Решение задач входит в программу сдачи ЕГЭ и билеты при поступлении в вуз.
Доказательство теорем
Теоретически S боковой поверхности ПП равна S б. п. = 2 (a+b)c. S полной поверхности равна Sполн. поверхности ПП=2 (ab+ac+bc).
Объем ПП равен произведению трех его боковых частей, выходящих из единой вершины (три измерения ПП): abc.
Доказательство: так как у ПП боковые ребра перпендикулярны основанию, то они являются и его высотами — h=AA1=c. Если в основании лежит прямоугольник, то Sосн=AB ⋅ AD=ab. Диагональ d ПП можно найти по формуле d2=a2+b2+c2, где a, b, c — измерения ПП.
Если в основании расположен прямоугольник, то △ ABD прямоугольный, значит, по теореме Пифагора BD2=AB2+AD2=a2+b2. Если все боковые грани перпендикулярны основной линии, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD.
Когда △ BB1D прямоугольный, то по теореме Пифагора B1D=BB12+BD2.
Решение задач
Задача 1: известны ПП: 3, 4, 12 см, необходимо найти длину главной диагонали фигуры.
Поиск ответа на вопрос начинается с выстраивания схематического изображения, на котором означаются величины. Используется формула B1D2 = AB2 + AD2 + AA12. После вычислений получается выражение b2=169, b=13.
Задача 2: ребра ПП, выходящие из общей точки, равны 3 и 4, общая S — 94. Нужно найти третье ребро, выходящее из той же вершины.
Ребра обозначаются а1 и а2, а неизвестное — а3. Площадь поверхности выражается S = 2 (a1a2 + a1a3 + a2a3).
Далее получаем a3 (a1 + a2) = S/2 — a1a2. Неизвестное ребро: a3 = S/2 — a1a2/a1 + a2 = 47−12/7 = 5.
Задача 3: два ребра прямоугольного параллелепипеда, выходящие из общей точки, составляют 72 и 18, диагональ равна 78. Нужно определить объем фигуры.
Для решения требуется найти диагональ по формуле вычисления квадратного корня из суммы (a2 + b2 + c2), где a, b, c — ребра фигуры. 78 — корень из суммы 722 + 182 + c2. Решение:
- 78 = корень из суммы 5508+с2
- 782 = 5508 + с2
- с2 = 6084 — 5508.
- С2 = 576.
Ответ: объем составляет 576.
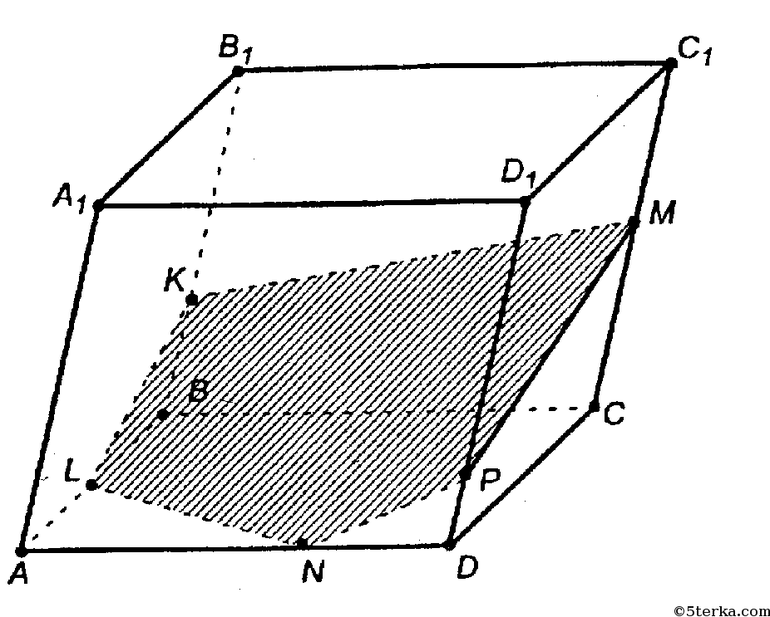
Задача 4: ребро наклонного параллелепипеда составляет 10 см, прямоугольник KLNM с измерениями 5 и 7 см является сечением фигуры, параллельным ребру. Нужно определить площадь боковой поверхности призмы.
KL и AD не являются равными, как пара ML и DC. Боковая S фигуры эквивалентна S сечения, умноженной на AA1, так как ребро перпендикулярно сечению. Ответ: 240 см².
Задача 5: ABCDA1B1C1D1 = 3, 4 см, боковое ребро — 12 см. Нужно определить диагональ ПП.
В основании лежит прямоугольник со сторонами АВ 3 см и AD 4 см. Боковое ребро составляет 3 см. BB1 является высотой ПП и равняется 12 см. Диагональ B1D2 = AB2 + BB1 2 += 9+16+144 = 169. B1D= 13 см.
Задача 6: основанием ПП служит квадрат, одна из вершин его верхнего основания одинаково удалена от всех вершин нижней части. Нужно найти высоту фигуры, если диагональ основания равна 8 см, а боковое ребро — 5 см.
Одна из вершин основания (F) равнозначно удалена от всех вершин нижнего основания параллелепипеда. Вместе с диагональю нижней части (AC) она образует равнобедренный ∆AFC. AF = AC по условию. AF является ребром фигуры.
В равнобедренном ∆AFC стороны одинаковы: AF=FC=5 см, AC=8 см. Высота ∆AFC будет являться высотой параллелепипеда.
Высота треугольника делит его основание пополам. По теореме Пифагора она равна:
- FK2 + (AC/2)2 = FC2;
- FK2 + 16 = 25;
- FK2 =25−16 = 9;
- FK = 3 см.
Высота фигуры составляет 3 см.
Установленные теоремы, доказательства, а также выведенные формулы помогают вычислить различные значения для фигуры.
На чтение 4 мин Просмотров 4.4к. Опубликовано 12 декабря, 2020
Параллелепипед — тело строгих геометрических форм, противоположные грани которого находятся в параллельных плоскостях. Все плоскости, или грани, включая основание, параллелограммы. Научно определение параллелепипеда — призма, основанием которой служит параллелограмм. Часто ученики затрудняются ответить, чем отличается параллелограмм от параллелепипеда. Отличие в том, что параллелограмм — фигура плоская, двухмерная, а параллелепипед — объемное геометрическое тело, протяженное в трех измерениях, имеющее ширину, высоту и длину. Как выглядит параллелепипед, посмотрите на рисунке:
Виды параллелепипеда
Параллелепипед — многогранник. Его ограничивают шесть плоскостей, два основания, и четыре боковые грани. Линии, по которым соединяются грани, называются ребрами, а точки, в которых сходятся три ребра — вершинами. У фигуры 8 вершин.
Если грани имеют общее ребро, то их называют смежными, а те, у которых такого ребра нет — противоположными. Это же касается и вершин, если они не лежат на одной грани, то их тоже называют противоположными. Высота, ширина и длина прямоугольного параллелепипеда называются измерениями, они выходят из одной вершины. Если фигура не прямоугольная, то измерения и ребра не совпадают.
При построении параллелепипеда на рисунке можно провести ряд дополнительных линий, которые помогают при вычислении объема, площади поверхности, неизвестных длин и других параметров. Если линии проходят через противоположные вершины, то их называют диагоналями. У параллелепипеда их насчитывается четыре.
В геометрии выделяют несколько типов параллелепипедов, которые отличаются некоторыми свойствами:
- Прямой — фигура, у которой боковые грани являются прямоугольниками;
- Прямоугольный — все грани прямоугольники, не только боковые, но и основания. Объемный прямоугольник — это т есть такой параллелепипед.
- Наклонный — боковые грани находятся по отношению к основанию под углами, отличными от 900;
- Ромбоэдр — все грани представляют собой равные ромбы;
- Куб — все грани квадратны.
Свойства параллелепипеда
Для всех типов параллелепипедов можно выделить общие свойства, характеризующие фигуру. Таких свойств немного, запомнить их не сложно:
- Диагонали параллелепипеда в точке пересечения делятся пополам;
- Параллелепипед симметричен относительно точки пересечения диагоналей;
- Любой отрезок, соединяющий две точки на гранях параллелепипеда и проходящий через точку пересечения диагоналей, делится пополам;
- Противоположные грани равны и параллельны (вытекает из определения);
- Сумма квадратов измерений равна квадрату диагонали.
Твердо запомнив эти свойства несложно решить большинство задач школьной геометрии.
Основные формулы параллелепипеда
Кроме свойств этой фигуры нужно запомнить ряд несложных формул. Конечно, в процессе решения задачи можно вывести эти выражения самостоятельно. Но часто на это нет времени, лучше воспользоваться готовыми шаблонами.
Формула площади боковой поверхности прямого параллелепипеда — одна из самых простых. Sб=Ро∙h. В этой формуле только три величины, но одна из них составная:
H – высота параллелепипеда;
Р – периметр, АВ+ВС+АD+ CD.
Воспользоваться такой формулой можно только в том случае, если известны длины сторон основы и высота.
Площадь полной поверхности параллелепипеда определяется по формуле Sп=Sб+2Sо.
Как найти площадь боковой поверхности мы знаем из предыдущего пункта, а площадь Sо рассчитывается в зависимости от вида четырехугольника, лежащего в основании.
Объем прямого параллелепипеда тоже найти несложно, для этого достаточно умножить площадь основания на высоту. Объём V=Sо∙h
Формулы для прямоугольного параллелепипеда тоже не отличаются сложностью:
Sб=2c(a+b) в этой формуле а и b – стороны основания, с – высота, равна длине бокового ребра.
Площадь полной поверхности равна Sп=2(ab+bc+ac);
Объем V=abc, то есть, произведение всех трех измерений.
Когда же приходится вычислять площади и объем произвольного параллелепипеда, то показанные формулы не всегда срабатывают. Необходимо использовать законы векторной геометрии. При вычислении объема параллелепипеда через длину диагонали, необходимо использовать проекции на разные оси. Видимая простота формул — это только основа для сложной работы, требующей пространственного воображения и смекалки.
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
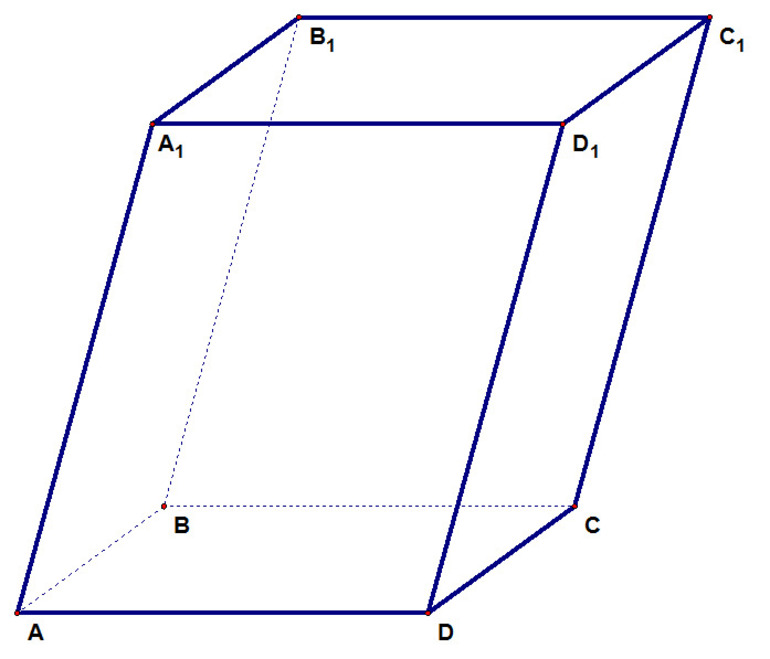
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ – длина;
$b$ – ширина;
$с$ – высота(она же боковое ребро);
$P_{осн}$ – периметр основания;
$S_{осн}$ – площадь основания;
$S_{бок}$ – площадь боковой поверхности;
$S_{п.п}$ – площадь полной поверхности;
$V$ – объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ – длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ – высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ – это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ – радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ – радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ – катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ – длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции. - Квадрат.
$S=a^2$, где $а$ – сторона квадрата.
Пример:
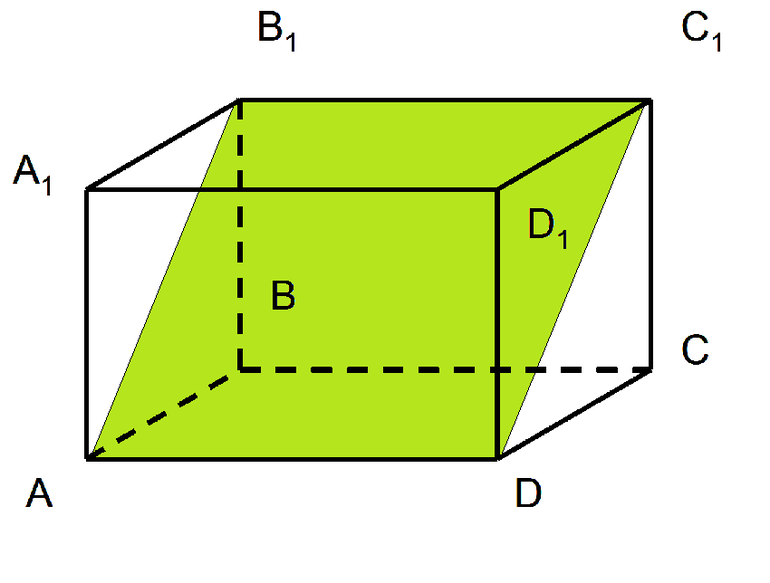
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ – стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
На прошлых занятиях мы рассматривали плоские фигуры.
В реальности же каждый предмет, какой бы он формы не был, занимает некоторую часть пространства.
Даже у самого тонкого листа бумаги имеется толщина.
Если взять стопку таких листов, то объем стопки бумаги будет хорошо заметен.
Эта информация доступна зарегистрированным пользователям
Раздел геометрии, в котором изучаются фигуры и их свойства в пространстве, называется стереометрией.
Слово стереометрия происходит от древнегреческого «стериос»- объемный, пространственный и «метрио»- измерять.
Базовыми фигурами в пространстве, как и на плоскости, является точка, прямая и плоскость, из которых образуются объемные геометрические фигуры, тела, пространства.
Геометрическое тело, состоящее из плоских многоугольников, называют многогранником.
Существует огромное множество многогранников: выпуклые, невыпуклые, правильные и т.д.
На данном уроке познакомимся с выпуклым прямоугольным многоугольником, который называется параллелепипед.
Эта информация доступна зарегистрированным пользователям
Выясним, как прямоугольный параллелепипед выглядит и из каких элементов он состоит.
Рассмотрим его свойства.
Научимся изображать данный многоугольник на плоскости и вычислять площадь его поверхности.
Разберем несколько примеров решения задач.
Каждый может себе представить и знает, как выглядят детские кубики.
С кубиками и конструктором из брусочков прямоугольной формы многие знакомы с раннего детства: строили домики, башенки, дороги, затем все это радостно рушили.
Эта информация доступна зарегистрированным пользователям
Всем известно, как выглядит коробка конфет или долька шоколада. Многие получали подарки в красивой красочной коробке с ярким бантом, читали книги с увлекательными рассказами и сказками.
Эта информация доступна зарегистрированным пользователям
Все эти знакомые вам предметы – это объемные тела, которые в реальности можно посмотреть, потрогать со всех сторон.
Если обратим внимание на форму, то заметим, что все изображенные объекты имеют некоторое сходство, они представляют собой прямоугольный параллелепипед.
Слово «параллелепипед» происходит от двух греческих слов: «параллелос» – идущие рядом и «опипедон» – плоскость.
Прямоугольный параллелепипед-это объемная геометрическая фигура, многогранник, состоящий из шести прямоугольников.
Прямоугольный параллелепипед – это пространственная фигура.
Плоские фигуры, такие как квадрат, прямоугольник, треугольник изобразить на плоскости легко, они являются её частью.
Любую объемную фигуру изобразить на плоскости затруднительно.
Многогранник необходимо изобразить так, чтобы была заметна объемность фигуры.
Для этого все линии многогранника, невидимые глазу, принято изображать на рисунке пунктирными линиями, а видимые – сплошными линиями.
Пунктирная линия дает возможность понять наблюдателю, как расположен многогранник и определить, откуда необходимо смотреть на него.
Если мы изобразим параллелепипед только сплошной линией, то на рисунке будут изображены различные четырехугольники, соединенные между собой, а объемного представления многоугольника данный рисунок не даст.
Эта информация доступна зарегистрированным пользователям
Даже если нам известно, что изображен прямоугольный параллелепипед, то все равно непонятно какой стороной расположен многогранник к наблюдателю.
Если невидимые линии на рисунке изобразить пунктирными линиями, то у фигуры сразу будет заметен объем.
Прямоугольный параллелепипед изображают так:
Эта информация доступна зарегистрированным пользователям
Прямоугольники, из которых состоит прямоугольный параллелепипед, называют гранями, причем противоположные грани его попарно равны.
Эта информация доступна зарегистрированным пользователям
Верхняя грань равна нижней, правая равна левой, передняя грань равна задней.
Грань, на которой стоит прямоугольный параллелепипед, называют нижним основанием, противоположную грань называют верхним основанием параллелепипеда.
Остальные четыре грани называют боковыми гранями.
Стороны граней называют ребрами параллелепипеда.
Эта информация доступна зарегистрированным пользователям
Концы ребер, т.е. вершины граней, называют вершинами параллелепипеда.
На рисунке вершины изображены точками.
Эта информация доступна зарегистрированным пользователям
Прямоугольный параллелепипед имеет три линейные величины (три измерения): ширину, длину и высоту.
Величину прямоугольного параллелепипеда определяют длинами трех ребер, исходящих из одной вершины.
Эта информация доступна зарегистрированным пользователям
Если все три величины прямоугольного параллелепипеда равны, то такой параллелепипед называют кубом.
Другими словами, куб – это частный случай параллелепипеда.
Куб – это правильный многоугольник, состоящий из шести одинаковых квадратов.
Куб по-другому называют правильный гексаэдр (от греческого «hex»- шесть и «hedra»- грань).
Куб выглядит так:
Эта информация доступна зарегистрированным пользователям
Он имеет все те же элементы, что и прямоугольный параллелепипед.
Эта информация доступна зарегистрированным пользователям
Все шесть граней куба равны, следовательно, и все 12 ребер между собой равны.
Куб так же имеет 2 основания: нижнее, на котором он стоит, и противоположное ему – верхнее.
Остальные четыре его грани – это боковые грани.
Эта информация доступна зарегистрированным пользователям
Платоновские тела
|
Тетраэдр |
Гексаэдр |
Октаэдр |
Додекаэдр |
Икосаэдр |
|
|
Внешний вид |
 |
 |
 |
 |
 |
|
Число и вид граней |
4 правильных треугольника |
6 квадратов |
8 правильных треугольников |
12 правильных пятиугольников |
20 правильных треугольников |
|
Число ребер |
6 |
12 |
12 |
30 |
30 |
|
Число вершин |
4 |
8 |
6 |
20 |
12 |
|
Число ребер, сходящихся в вершине |
3 |
3 |
4 |
3 |
5 |
|
Символьное значение |
Огонь |
Земля |
Воздух |
Все сущее (все мироздание) |
Вода |
Эта информация доступна зарегистрированным пользователям
Если посмотреть вокруг, то мы можем заметить огромное множество объектов, имеющих форму прямоугольного параллелепипеда или напоминающих его форму.
Так, например, большинство зданий и помещений, шкаф (тумбочка), столешница, аквариум, коробка, кирпичи и многое другое представляют собой прямоугольный параллелепипед.
Эта информация доступна зарегистрированным пользователям
Такой многогранник имеет широкое применение в различных областях нашей жизни, и это неспроста:
1) прямоугольная форма параллелепипеда удобна для деления целого на части
2) объекты прямоугольной формы легко надстраивать и совмещать
3) прямоугольный параллелепипед является одним из самых устойчивых многогранников
Часто приходится определять площадь поверхности объекта, имеющего форму прямоугольного параллелепипеда.
Давайте разберемся, как и с помощью каких формул можно вычислить площадь его поверхности.
Допустим, у нас есть коробка, имеющая форму прямоугольного параллелепипеда.
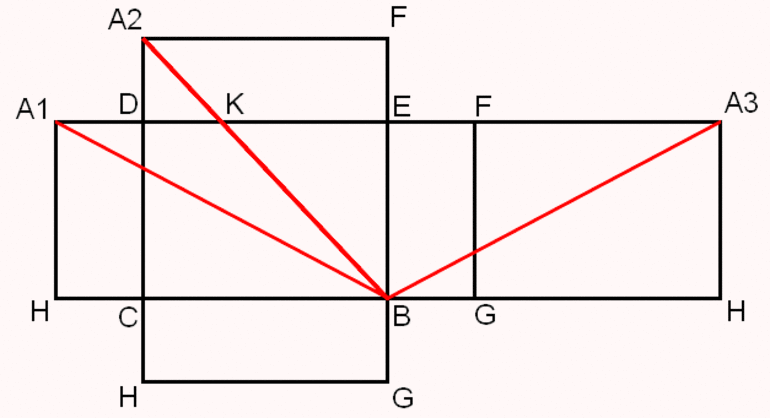
Попробуем изобразить развертку данного геометрического тела.
Развертка параллелепипеда – это изображение его поверхности в виде плоской фигуры, составленной из двух равных оснований: прямоугольников и четырех боковых граней (прямоугольников, попарно равных друг другу).
Эта информация доступна зарегистрированным пользователям
Площадь этой развертки- это и есть площадь поверхности прямоугольного параллелепипеда.
Так как прямоугольный параллелепипед состоит из шести граней, имеющих форму прямоугольников, причем противоположные грани равны по величине, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей всех его шести граней.
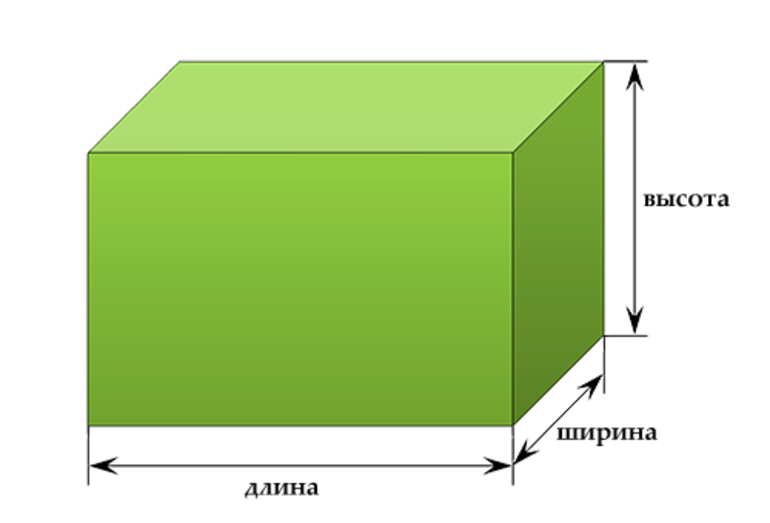
Пусть для нашего прямоугольного параллелепипеда три ребра, выходящие из одной вершины, имеют значения а, b, h.
Эта информация доступна зарегистрированным пользователям
а– ширина прямоугольного параллелепипеда
b– длина прямоугольного параллелепипеда
h– высота прямоугольного параллелепипеда
Найдем площадь всех граней.
Воспользуемся формулой для расчета площади прямоугольника: площадь прямоугольника равна произведению его ширины на длину.
Ребра, лежащие напротив ребер а, b, h, будут иметь такие же значения длины, так как противолежащие ребра прямоугольного параллелепипеда равны.
В таком случае получаем:
1) Площадь нижнего основания равна произведению (a ∙ b)
2) Площадь верхнего основания также равна произведению (a ∙ b)
3) Площадь левой боковой и правой боковой граней равны, как противолежащие, площадь каждой из них определяется произведением (b ∙ h)
4) Передняя и задняя боковые грани равны, а значение площади каждой из них будет определяться произведением (а ∙ h)
Сложим площади всех граней прямоугольного параллелепипеда, получим общую площадь его поверхности.
Эта информация доступна зарегистрированным пользователям
Упростим выражение, вынесем 2 за скобку.
Формула площади поверхности прямоугольного параллелепипеда будет выглядеть так:
Эта информация доступна зарегистрированным пользователям
Площадь двух оснований прямоугольного параллелепипеда (это два прямоугольника) найдем по формуле:
Sосн = 2 (a ∙ b).
Площадь боковой поверхности прямоугольного параллелепипеда можно найти по формуле:
Sбок = 2h ∙ (a + b).
В нашем случае а, b– это стороны основания, h– это высота прямоугольного параллелепипеда (боковое ребро).
Так как основанием прямоугольного параллелепипеда является прямоугольник, то периметр основания прямоугольного параллелепипеда определяется равенством
Роснов = 2 ∙ (a + b).
Подставим Роснов в формулу Sбок = 2h ∙ (a + b) вместо выражения 2 ∙ (a + b).
Тогда площадь боковой поверхности можно найти так:
Sбок = Роснов ∙ h.
Определим площадь поверхности куба.
Известно, что куб – это прямоугольный параллелепипед, поверхность которого состоит из шести одинаковых граней, имеющих форму квадрата.
Чтобы найти площадь поверхности куба, необходимо сложить площади всех его граней.
Площадь одной грани куба найдем по формуле площади квадрата:
S = a2
а– это сторона квадрата (ребро куба).
Так как все 6 граней куба представляют собой равные по площади квадраты, следовательно, чтобы найти площадь всей поверхности куба, необходимо площадь одной грани умножить на их количество.
Формула площади поверхности куба выглядит так:
Эта информация доступна зарегистрированным пользователям
Рассмотрим решение нескольких практических задач.
В процессе любого строительства или ремонта очень часто встает вопрос о том, сколько необходимо потратить строительного и отделочного материала или как рассчитать расход краски.
Задача №1.
Какое количество краски понадобится, чтобы полностью покрасить бак прямоугольной формы?
Ширина бака 2 метра, длина 3 метра, высота 1 метр.
Известно, что на 1 м2 расходуется 200 г краски.
Эта информация доступна зарегистрированным пользователям
Чтобы рассчитать количество краски, которое нужно затратить на покраску бака, необходимо определить площадь окрашиваемой поверхности, затем, зная норму расхода краски на единицу площади, можно рассчитать расход краски на всю окрашиваемую поверхность.
Пусть m1– масса краски, которая расходуется на 1 м2
m2– масса краски, которая необходима для покраски всего бака.
Эта информация доступна зарегистрированным пользователям
Задача №2
Сколько квадратных метров стекла понадобится на изготовление аквариума кубической формы длиной 100 см?
Эта информация доступна зарегистрированным пользователям
Для вычисления площади поверхности аквариума в квадратных метрах необходимо длину аквариума перевести из сантиметров в метры.
Вспомним, 1 м = 100 см.
Эта информация доступна зарегистрированным пользователям
Если бы аквариум необходимо было изготовить только из боковых стенок и основания, то из стекла пришлось бы вырезать всего 5 квадратных граней.
В таком случае формула для вычисления площади поверхности аквариума приняла бы вид
S = 5 а2.
Задача №3
Хозяйка решила покрасить стены в комнате.
Вычислите площадь поверхности стен комнаты, в которой имеется дверной проем площадью 2 м2 и оконный проем площадью 1 м2.
Комната имеет форму прямоугольного параллелепипеда.
Ширина комнаты 3 метра, длина комнаты 4 метра, высота комнаты 3 метра.
Эта информация доступна зарегистрированным пользователям
Пусть Sc– общая площадь стен комнаты.
Sд– площадь дверного проема.
Sо– площадь оконного проема.
S– площадь стен комнаты за исключением площади дверного и оконного проемов.
Эта информация доступна зарегистрированным пользователям