Решение:
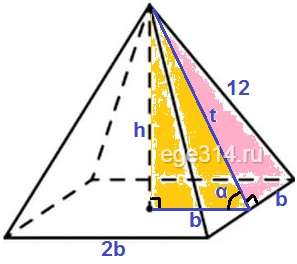
Пусть 2b – сторона основания пирамиды. Зная тангенс угла, выразим высоту пирамиды, через b:
Из оранжевого прямоугольного треугольника, через теорему Пифагора, выразим t2:
t2 = h2 + b2
t2 = (√7·b)2 + b2
t2 = 7·b2 + b2 = 8b2
Из розового прямоугольного треугольника, по теореме Пифагора найдём b:
122 = b2 + t2
144 = b2 + 8b2
144 = 9b2
b2 = 144/9 = 16
b = √16 = 4
Найдём сторону основания пирамиды 2b:
2b = 2·4 = 8
Ответ: 4.
Тренировочный вариант 360 от Ларина Задание 5 (8) ЕГЭ № задачи в базе 2962
В правильной треугольной пирамиде боковое ребро равно 15, а тангенс угла между боковой гранью и плоскостью основания равен
sqrt23
. Найдите сторону основания пирамиды
Ответ: 10
Ключевые слова:
Задания ЕГЭ части 1 | Ларин варианты | Задачи 2 стереометрия | Геометрия | Стереометрия | Пирамида | ЕГЭ по математике 2022 | 360 тренировочный вариант от Ларина |
ФИПИ 2023 🔥 …
Примечание: В правильной треугольной пирамиде боковое ребро равно 15, а тангенс угла между боковой гранью и плоскостью основания равен ! Тренировочный вариант 360 от Ларина Задание 5 (8) ЕГЭ
10%
Рейтинг сложности задачи:
В правильной треугольной пирамиде боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Спрятать решение
Решение.
Введём обозначения, как показано на рисунке. Выразим длину стороны AC через длину боковой стороны
Высота правильного треугольника выражается через его сторону:
Точкой O высота AH делится в отношении 2 : 1, поэтому
Угол SHO равен углу между боковой гранью и плоскостью основания. Из прямоугольного треугольника
Из прямоугольного треугольника AOS по теореме Пифагора:
Откуда
Ответ: 8.
Кодификатор ФИПИ/Решу ЕГЭ:

в правильной четырехугольной пирамиде боковое ребро равно 22 а тангенс угла между боковой гранью и плоскость основания равен корень из 14. найти сторону основания пирамиды
Светило науки – 9801 ответ – 46531 помощь
Угол между боковой гранью и плоскостью основания измеряется линейным углом между апофемой А и её проекцией на основание КО, равной половине стороны основания (квадрата).
Обозначим половину стороны основания за х.
Квадрат апофемы равен: А² = 22² – х².
Теперь рассмотрим прямоугольный треугольник SKO.
По заданию SO/OК = √14, или SO²/OК² = 14.
По свойству квадрата ОК = х.
Тогда А² = х² + 14х² = 15х².
Заменим А² = 22² – х².
Получаем 22² – х² = 15х²,
484 = 16х²,
х² = 484/16 = 121/4
х =√(121/4) = 11/2.
Находим величину стороны основания: а = (11/2)*2 = 11.
Сторона основания пирамиды является стороной правильного многоугольника, исходя из этого, можно найти все параметры пирамиды, связанные с основанием, воспользовавшись формулами для правильных многоугольников.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла. (рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
Зная боковое ребро в совокупности со стороной основания, можно вычислить высоту пирамиды и ее апофему из прямоугольных треугольников, которые они образуют. (рис.34.5, 35.1)
h=√(b^2-R^2 )=√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 )
l=√(b^2-a^2/4)
Косинус угла между боковым ребром и основанием будет равен отношению радиуса окружности, описанной вокруг основания, к боковому ребру пирамиды, а косинус угла между апофемой и основанием – отношению радиуса вписанной в основание окружности к апофеме. (рис.34.4,34.5)
cosα=R/b=a/(2b sin〖(180°)/n〗 )
cosβ=r/l=a/(2 tan〖(180°)/n〗 √(b^2-a^2/4))
Площадь боковой поверхности пирамиды складывается из площадей треугольников, являющихся ее гранями, каждая из которых равна половине произведения апофемы на сторону основания, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания.
S_(б.п.)=lan/2=(√(b^2-a^2/4) an)/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))=an(√(b^2-a^2/4)/2+a/(4 tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо вычислить треть от произведения ее высоты на площадь основания, последовательно подставив выражения для площади и высоты в формулу.
V=1/3 S_(осн.) h=(na^2 √(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(12 tan〖(180°)/n〗 )
Радиус сферы, которая может быть вписана в пирамиду, равен трем объемам, деленным на площадь полной поверхности пирамиды, а радиус сферы, описанной вокруг пирамиды – квадрату бокового ребра, деленному на две высоты. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =(a√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(tan〖(180°)/n〗 (2√(b^2-a^2/4)+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=b^2/(2√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))