 Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.
Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.
Обозначения
- $SABCDEF$ — правильная шестиугольная пирамида
- $O$ — центр основания пирамиды
- $a$ — длина стороны основания пирамиды
- $h$ — длина бокового ребра пирамиды
- $S_{text{осн.}}$ — площадь основания пирамиды
- $V_{text{пирамиды}}$ — объем пирамиды
Площадь основания пирамиды
В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$
Правильный шестиугольник в основании пирамиды
 По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a, angle EOA=120^{circ}$. По свойствам равнобедренного треугольника $$ AE=acdotsqrt{2(1-cos EOA)}=sqrt{3}cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=sqrt{3}cdot a $, $FM=MO=frac{1}{2}cdot a$.
По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a, angle EOA=120^{circ}$. По свойствам равнобедренного треугольника $$ AE=acdotsqrt{2(1-cos EOA)}=sqrt{3}cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=sqrt{3}cdot a $, $FM=MO=frac{1}{2}cdot a$.
Находим $SO$
Прямая $SO$ является высотой пирамиды, поэтому $angle SOF=90^{circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a, FS=h$. По свойствам прямоугольного треугольника $$ SO=sqrt{FS^2-FO^2}=sqrt{h^2-a^2} $$
Объем пирамиды
Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{пирамиды}}=frac{1}{3}cdot S_{text{осн.}}cdot SO=frac{sqrt{3}}{2}cdot a^2 cdot sqrt{h^2-a^2} $$
Находим $ST$ и $TO$
 Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=frac{sqrt{3}}{2}cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=sqrt{SO^2+TO^2}=sqrt{h^2-frac{1}{4}cdot a^2} $$
Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=frac{sqrt{3}}{2}cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=sqrt{SO^2+TO^2}=sqrt{h^2-frac{1}{4}cdot a^2} $$
Сторона основания пирамиды является стороной правильного многоугольника, исходя из этого, можно найти все параметры пирамиды, связанные с основанием, воспользовавшись формулами для правильных многоугольников.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла. (рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
Зная боковое ребро в совокупности со стороной основания, можно вычислить высоту пирамиды и ее апофему из прямоугольных треугольников, которые они образуют. (рис.34.5, 35.1)
h=√(b^2-R^2 )=√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 )
l=√(b^2-a^2/4)
Косинус угла между боковым ребром и основанием будет равен отношению радиуса окружности, описанной вокруг основания, к боковому ребру пирамиды, а косинус угла между апофемой и основанием – отношению радиуса вписанной в основание окружности к апофеме. (рис.34.4,34.5)
cosα=R/b=a/(2b sin〖(180°)/n〗 )
cosβ=r/l=a/(2 tan〖(180°)/n〗 √(b^2-a^2/4))
Площадь боковой поверхности пирамиды складывается из площадей треугольников, являющихся ее гранями, каждая из которых равна половине произведения апофемы на сторону основания, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания.
S_(б.п.)=lan/2=(√(b^2-a^2/4) an)/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))=an(√(b^2-a^2/4)/2+a/(4 tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо вычислить треть от произведения ее высоты на площадь основания, последовательно подставив выражения для площади и высоты в формулу.
V=1/3 S_(осн.) h=(na^2 √(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(12 tan〖(180°)/n〗 )
Радиус сферы, которая может быть вписана в пирамиду, равен трем объемам, деленным на площадь полной поверхности пирамиды, а радиус сферы, описанной вокруг пирамиды – квадрату бокового ребра, деленному на две высоты. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =(a√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(tan〖(180°)/n〗 (2√(b^2-a^2/4)+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=b^2/(2√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))

Rizik25
+10
Решено
7 лет назад
Геометрия
10 – 11 классы
Помогите пожалуйста решить задачу по геометрии!!! Высота правильной шестиугольной пирамиды равна 4. Боковое ребро равно 5. Найдите сторону основания пирамиды?
Смотреть ответ
1
Ответ
3
(5 оценок)
5

kat99rus
7 лет назад
Светило науки – 59 ответов – 0 раз оказано помощи
дано:ABCDEFS пирамида
so высота=4
sb боковое ребро=5
решение:
1. SBO ТРЕУГОЛЬНИК
SO ВЫСОТА
OB = КОРЕНЬ КВАДРАТНЫЙ ИЗ 5^2-4^2=3
OB- радиус описанно окружности
2. т.к. ABCDEF правильный шестиугольник следовательно OB=AB
ОТВЕТ:3
(5 оценок)
https://vashotvet.com/task/5015086
Задания
Версия для печати и копирования в MS Word
Тип 2 № 27180 

i
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Спрятать решение
Решение.
Площадь основания равна
Из формулы для объема пирамиды найдем высоту:
В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем боковое ребро пирамиды по теореме Пифагора:
Ответ: 7.
Аналоги к заданию № 27180: 76787 76789 76791 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Спрятать решение
·
Видеокурс
·
Помощь
Как найти сторону основания пирамиды
Задачи на вычисление стороны основания пирамиды составляют в задачнике по геометрии довольно большой раздел. Очень многое зависит от того, какая гемоетрическая фигура лежит в основании, а также от того, что дано в условиях задачи.

Вам понадобится
- – чертежные принадлежности;
- – тетрадь в клетку;
- – теорема синусов;
- – теорема Пифагора;
- – калькулятор.
Инструкция
В школьном курсе геометрии рассматриваются главным образом пирамиды, в основании которых лежит правильный многоугольник, то есть такой, у которого все стороны равны. Проекция вершины пирамиды совпадает с центром ее основания. Начертите пирамиду, в основании которой лежит равносторонний треугольник. В условиях могут быть даны:
– длина бокового ребра пирамиды и угол его с ребром между боковой гранью и основанием;
– длина бокового ребра и высота боковой грани;
– длина бокового ребра и высота пирамиды.
Если известны боковое ребро и угол, задача решается несколько иначе. Вспомните, что собой представляет каждая боковая грань пирамиды, в основании которой лежит равносторонний многоугольник. Это равнобедренный треугольник. Проведите его высоту, которая одновременно является биссектрисой и медианой. То есть половина стороны основания a/2=L*cosA, где а – сторона основания пирамиды, L – длина ребра. Чтобы найти размер стороны основания, достаточно полученный результат умножить на 2.
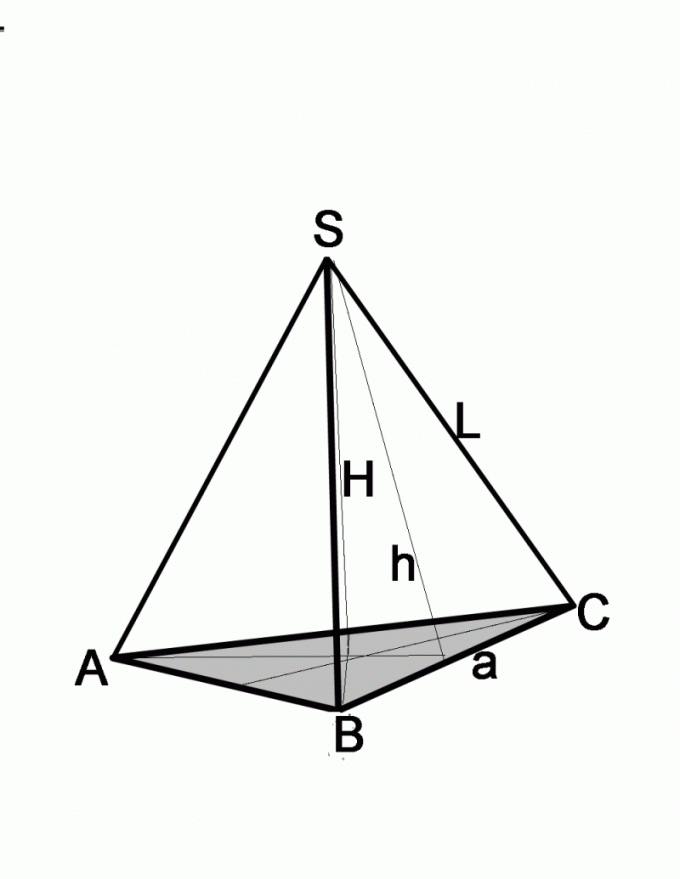
Если в задаче даны высота боковой грани и длина ребра, найдите сторону основания по теореме Пифагора. Боковая грань в данном случае будет гипотенузой, известная высота –з одним из катетов. Чтобы найти длину второго катета, нужно из квадрата гипотенузы вычесть квадрат второго катета, то есть (a/2)2=L2-h2, где а – сторона основания, L – длина боковой грани, h – высота боковой грани.
В этом случае нужно выполнить дополнительное построение, чтобы можно было оперировать тригонометрическими функциями. Вам даны боковое ребро L и высота пирамиды H, которая соединяет вершину пирамиды с центром основания. Из точки пересечения высоты с плоскостью основания проведите отрезок, соединив эту точку с одним из углов основания. У вас получился прямоугольный треугольник, гипотенузой которого является боковое ребро, одним из катетов – высота пирамиды. По этим данным легко найти второй катет треугольника, для этого достаточно из квадрата бокового ребра L вычесть квадрат высоты H. Дальнейшие действия зависят от того, какая именно фигура лежит в основании.
Вспомните свойства равностороннего треугольника. У него высоты одновременно являются биссектрисами и медианами. В точке пересечения они делятся пополам. То есть получается, что вы нашли половину высоты основания. Для удобства вычислений проведите все три высоты. Вы увидите, что отрезок, квадрат длины которого вы уже нашли, является гипотенузой прямоугольного треугольника. Извлеките квадратный корень. Вам известен и острый угол – 30°, так что найти половину стороны основания не составит особого труда, применив теорему косинусов.
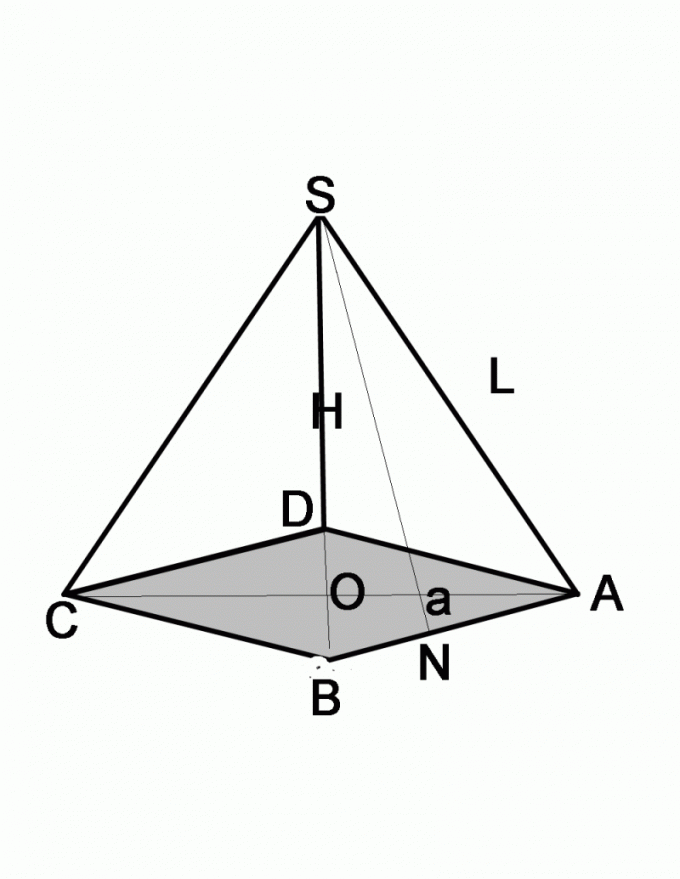
Для пирамиды, в основании которой лежит правильный четырехугольник, алгоритм будет тем же самым. Если вы вычтите из квадрата бокового ребра квадрат высоты пирамиды, получите возведенную в квадрат половину диагонали основания. Извлеките корень, найдите размер диагонали, которая одновременно является гипотенузой равнобедренного прямоугольного треугольника. Размер любого из катетов найдите по теореме Пифагора, синусов или косинусов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
