Как найти сторону основания правильной шестиугольной призмы

Одним из фундаментальных объектов в геометрии является многоугольник. Если рассматривать фигуру в трёхмерном пространстве, то с помощью двух таких геометрических тел с шестью углами можно построит правильную шестиугольную призму. При этом боковые грани обязательно будут прямоугольниками. По своему виду такая фигура напоминает пчелиные соты, поэтому она и интересна для изучения архитекторам и математикам.

Общие сведения

Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.

Кроме основания и граней, в состав стереофигуры входит:

• высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
• боковые рёбра — стороны, являющиеся общими для боковых граней;
• вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
• диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
• диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.

Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.

В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.

Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.

Свойства шестигранника

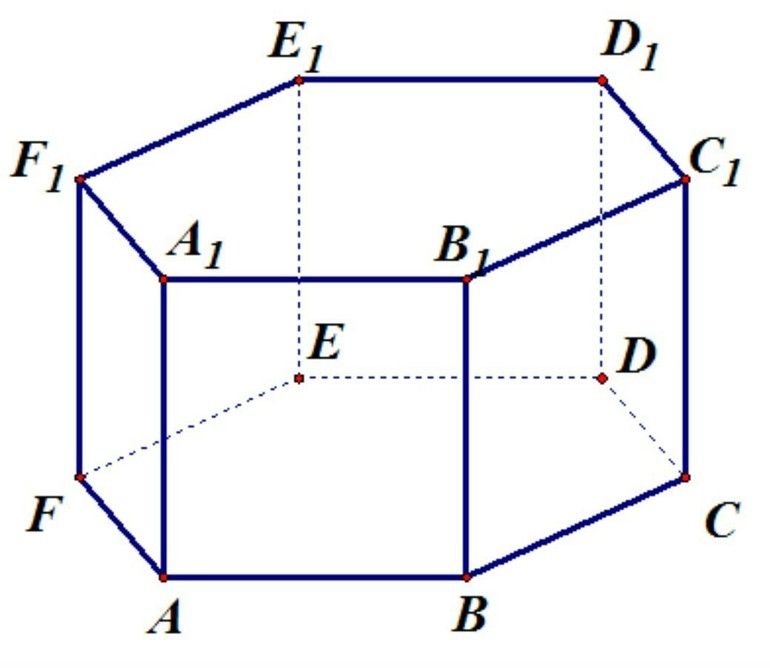
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.

Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a ² * √ 3) / 2, где: а — сторона многоугольника.

Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a ² * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.

Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a² * h).

Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .

Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.

По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1² + AE²)= √(h² + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1² + BE²) = √(h² + 4 *a) = √5 *a. Сторона FE1 = √(FE² + EE²) = √(h² + a²) = √2 *a.

Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h² + a²), что и следовало доказать.

Решение простого примера

Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.

Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.

Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.

Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.

С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.

Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E² = C1C² + CE = 2² + (4 c3) ². C1E² = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.

Задача высокого уровня

Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.

Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.

Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.

Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.

Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R² = (12 * 2) / 3 √ 3 = 8 /√3.

Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a² * sin60 / 2 = (R² * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.

Предыдущая

ГеометрияТочка пересечения биссектрис – свойства, теорема и соотношения

Следующая

ГеометрияЭлементы треугольника – формулы вычисления основных параметров

Общие сведения

Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.

Кроме основания и граней, в состав стереофигуры входит:

• высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
• боковые рёбра — стороны, являющиеся общими для боковых граней;
• вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
• диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
• диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.

Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.

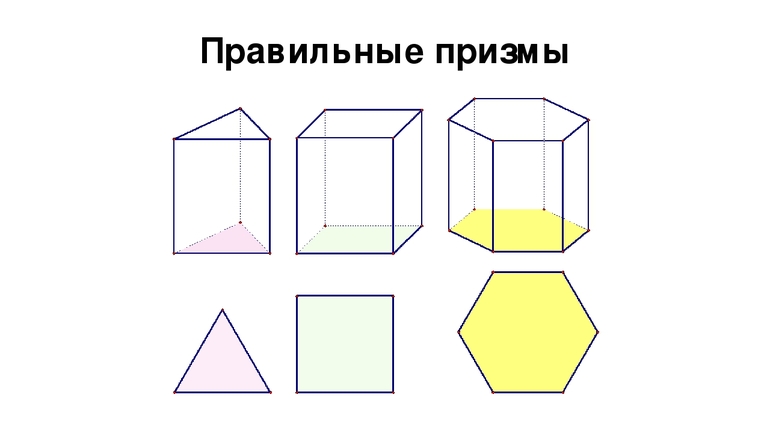
В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.

Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.

Свойства шестигранника

Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.

Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

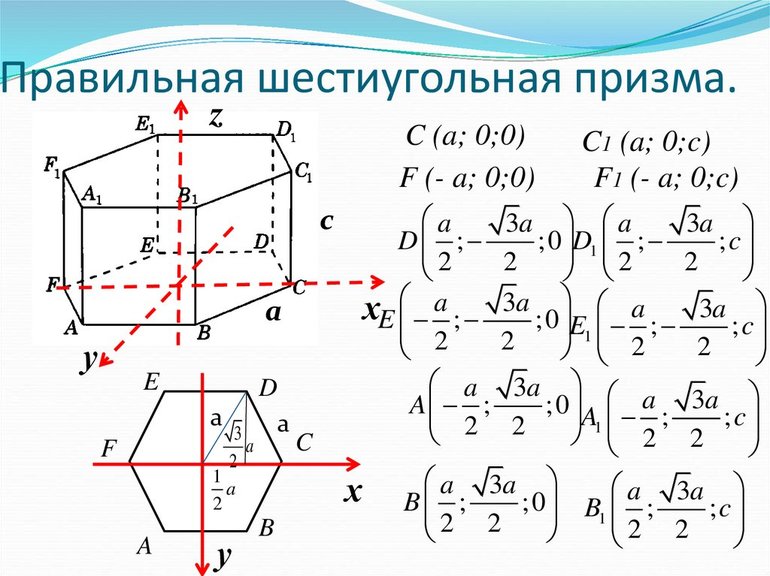
1. Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a ² * √ 3) / 2, где: а — сторона многоугольника.
2. Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a ² * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.
3. Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a² * h).

Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .

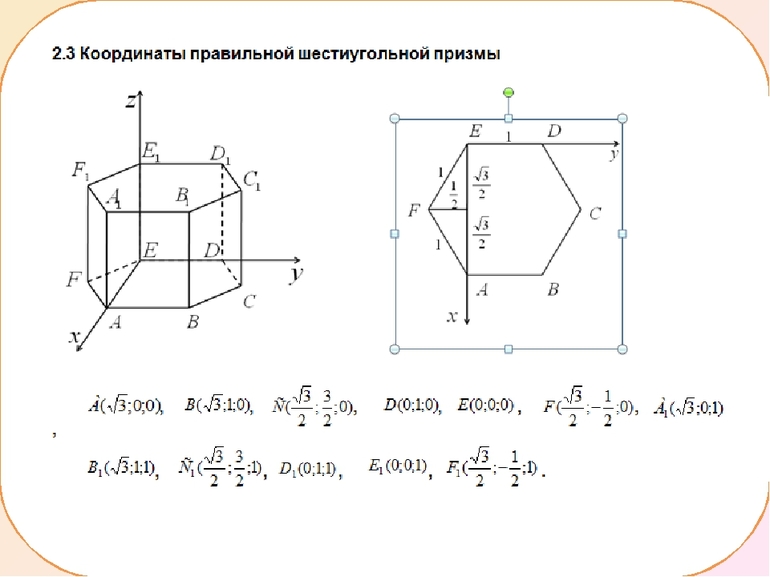
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.

По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1² + AE²)= √(h² + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1² + BE²) = √(h² + 4 *a) = √5 *a. Сторона FE1 = √(FE² + EE²) = √(h² + a²) = √2 *a.

Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h² + a²), что и следовало доказать.

Решение простого примера

Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.

Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.

Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.

Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.

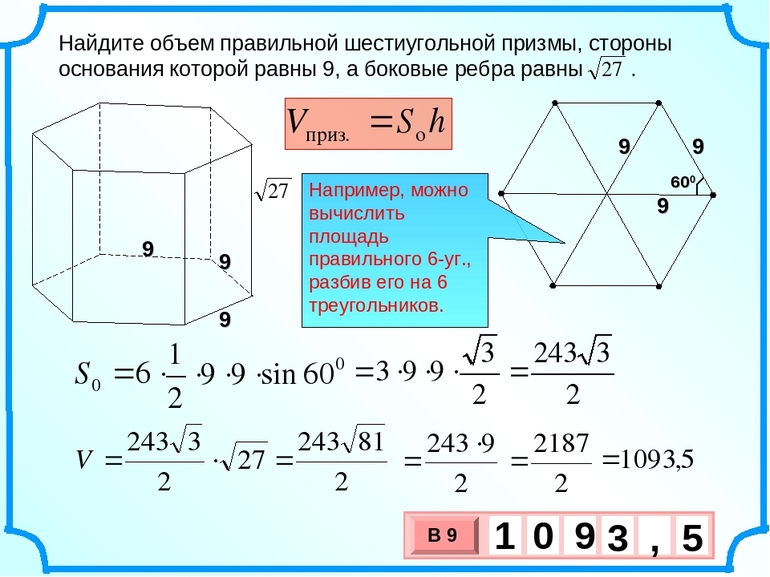
С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.

Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E² = C1C² + CE = 2² + (4 c3) ². C1E² = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.

Задача высокого уровня

Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.

Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.

Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.

Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.

Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R² = (12 * 2) / 3 √ 3 = 8 /√3.

Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a² * sin60 / 2 = (R² * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.

Проверяемые элементы содержания и виды деятельности: владение понятиями о стереометрических фигурах; знание их свойств; знание формул для вычисления площадей поверхностей и объемов тел; умение применять эти знания при решении задач.

Ориентировочное время выполнения учащимися: 10—15 минут.

Типы заданий:

• Элементы, площадь поверхности, объем стереометрических фигур.

Особенности экзаменационных заданий по стереометрии

Задания этого вида представляют собой стереометрические задания на установление взаимосвязи между основными элементами многогранников и круглых тел, а также на использование формул для вычисления их площадей поверхностей и объемов. Вычислительной трудности задания не представляют; решение, как правило, сводится к использованию одной-двух формул. Соответствующие формулы нужно знать наизусть.

Куб

Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для него выполнены все их свойства. Кроме того, если а — длина ребра куба,  — диагональ основания,  — диагональ куба,  — площадь полной поверхности, а V — объем куба, то справедливы формулы:

Призма. Прямоугольный параллелепипед

Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.

Правильной призмой называется прямая призма, основание которой — правильный многоугольник.

Прямая призма

Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы — прямоугольники.

Соотношения для прямой призмы

Пусть H — высота прямой призмы, AA₁ — боковое ребро,  — периметр основания,  — площадь основания,  — площадь боковой поверхности,  — площадь полной поверхности, V — объем прямой призмы. Тогда имеют место следующие соотношения:

Особенности правильной шестиугольной призмы

В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.

— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.

— Меньшая диагональ правильного шестиугольника в раз больше его стороны.

— Угол между сторонами правильного шестиугольника равен 120°.

— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.

— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Пирамида

Пусть вне плоскости многоугольника задана точка P. Тогда фигура, образованная треугольниками , и многоугольником вместе с их внутренними областями называется пирамидой (n-угольной пирамидой).

Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.

Соотношения для правильной пирамиды

Пусть H — высота правильной пирамиды, h — ее апофема,  — периметр основания пирамиды,  — площадь основания,  — площадь боковой поверхности,  — площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место следующие соотношения:

Сечения

Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).

Теоремы, используемые при построении сечений

Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.

Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости

Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.

Алгоритм построения сечений

Для построения сечений рекомендуем пользоваться следующим алгоритмом.

1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.

2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.

3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.

Для контроля правильности построенного сечения, проверяйте, что:

— все вершины сечения лежат на рёбрах многогранника;

— все стороны сечения лежат в гранях многогранника;

— в каждой грани многогранника лежит не более одной стороны сечения.

Цилиндр

Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.

Соотношения для цилиндра

Пусть h — высота цилиндра, r — радиус основания, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место следующие соотношения:

Конус

Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.

Соотношения для конуса

Пусть h — высота конуса, r — радиус основания, l — образующая, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем конуса. Тогда имеют место следующие соотношения:

Сфера и шар

Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность шара. Пусть R — радиус шара, S — площадь сферы, V — объем шара. Тогда имеют место следующие соотношения:

Комбинации круглых тел. Вписанные сферы

Сфера называется вписанной в цилиндр, если она касается обоих оснований цилиндра и каждой его образующей.

Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.

Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и всех его образующих.

Теорема 1: В прямой круговой цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания. Причём центр сферы есть середина оси цилиндра.

Теорема 2: В любой прямой круговой конус можно вписать сферу. Причём центр сферы есть точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.

Теорема 3. В усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть середина оси усечённого конуса.

Комбинации круглых тел. Описанные сферы

Сфера называется описанной около цилиндра, если окружности его оснований лежат на сфере.

Сфера называется описанной около конуса, если вершина конуса и его основание лежат на сфере.

Теорема 1: около цилиндра можно описать сферу тогда и только тогда, когда он прямой круговой. Причём центр сферы есть середина оси цилиндра.

Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.

Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной какой-либо из его образующих и проходящей через ее середину.

Комбинации конуса и цилиндра

Цилиндр называется вписанным в конус, если одно его основание лежит на основании конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию. Конус в этом случае называется описанным вокруг цилиндра.

Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.

Комбинации многогранников и круглых тел. Описанные сферы

Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. Многогранник называется в этом случае вписанным в сферу.

Возможность описать сферу около многогранника означает существование точки (центра сферы), равноудалённой ото всех вершин многогранника.

Теорема 1: если из центра описанной около многогранника сферы опустить перпендикуляр на какое-либо из его рёбер, то основание этого перпендикуляра разделит ребро на две равные части.

Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного около соответствующей грани.

Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около соответствующей грани.

Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.

Комбинации многогранников и круглых тел. Вписанные сферы

Сфера называется вписанной в многогранник, если все его грани касаются этой сферы. Многогранник называется в этом случае описанным около сферы.

Теорема: если в многогранник с площадью поверхности S и объёмом V вписан шар радиуса r, то справедливо соотношение:

Комбинации конуса, цилиндра и многогранников

В условиях задач встречаются также следующие понятия, не входящие в школьные учебники, которые уточняются непосредственно в условиях задач. Приведем наиболее употребительные из них.

Цилиндр вписан в призму: основания цилиндра вписаны в основания призмы.

Цилиндр описан вокруг призмы: основания цилиндра описаны вокруг оснований призмы.

Цилиндр вписан в пирамиду: одно из основание цилиндра вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание цилиндра принадлежит основанию пирамиды.

Цилиндр описан вокруг пирамиды: вершина пирамиды принадлежит одному из оснований цилиндра, а другое его основание описано вокруг основания пирамиды.

Конус вписан в призму: основание конуса вписано в основание призмы, а вершина конуса принадлежит противоположному основанию призмы.

Конус описан вокруг призмы: одно из оснований призмы вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание призмы вписано в основание конуса.

Конус вписан в пирамиду: их вершины совпадают, а основание конуса вписано в основание пирамиды. Вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой.

Конус описан вокруг пирамиды: их вершины совпадают, а основание конуса описано вокруг основания пирамиды.

Правильная шестиугольная призма — призма, в основаниях которой лежат два правильных шестиугольника, а все боковые грани строго перпендикулярны этим основаниям.

Обозначения

• $ABCDEFA_1B_1C_1D_1E_1F_1$ — правильная шестиугольная призма
• $a$ — длина стороны основания призмы
• $h$ — длина бокового ребра призмы
• $S_{text{осн.}}$ — площадь основания призмы
• $S_{text{бок.}}$ — площадь боковой грани призмы
• $S_{text{полн.}}$ — площадь полной поверхности призмы
• $V_{text{призмы}}$ — объем призмы

Площадь оснований призмы

В основаниях призмы находятся правильные шестиугольники со стороной $a$. По свойствам правильного шестиугольника, площадь оснований призмы равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$ Таким образом, получается, что $S_{ABCDEF}=S_{A_1B_1C_1D_1E_1F_1}=frac{3sqrt{3}}{2}cdot a^2$.

Площадь полной поверхности призмы

Площадь полной поверхности призмы складывается из площадей боковых граней призмы и площадей ее оснований. Каждая из боковых граней призмы является прямоугольником со сторонами $a$ и $h$. Следовательно, по свойствам прямоугольника $$ S_{text{бок.}}=acdot h $$ У призмы шесть боковых граней и два основания, следовательно, площадь ее полной поверхности равна $$ S_{text{полн.}}=6cdot S_{text{бок.}}+2cdot S_{text{осн.}}=6cdot acdot h+2cdot frac{3sqrt{3}}{2}cdot a^2$$

Объем призмы

Объем призмы вычисляется как произведение площади ее основания на ее высоту. Высотой правильной призмы является любое из ее боковых ребер, например, ребро $AA_1$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{призмы}}=S_{text{осн.}}cdot AA_1=frac{3sqrt{3}}{2}cdot a^2cdot h $$

Правильный шестиугольник в основаниях призмы

Рассматриваем правильный шестиугольник ABCDEF, лежащий в основании призмы. Проводим отрезки AD, BE и CF. Пусть пересечением этих отрезков является точка O. По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a, angle EOA=120^{circ}$. По свойствам равнобедренного треугольника $$ AE=acdotsqrt{2(1-cos EOA)}=sqrt{3}cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=sqrt{3}cdot a $, $FM=MO=frac{1}{2}cdot a$.

Находим $EA_1$

В треугольнике $AEA_1$:

• $AA_1=h$
• $AE=sqrt{3}cdot a$ — как мы только что выяснили
• $angle EAA_1=90^{circ}$ — по свойствам правильной призмы

Таким образом, получается, что треугольник $AEA_1$ прямоугольный. По свойствам прямоугольного треугольника $$ EA_1=sqrt{AA_1^2+AE^2}=sqrt{h^2+3cdot a^2} $$ Если $h=a$, то тогда $$ EA_1=2cdot a $$ После аналогичных рассуждений получаем, что $FB_1=AC_1=BD_1=CE_1=DF_1=sqrt{h^2+3cdot a^2}$.

Находим $EB_1$

В треугольнике $BEB_1$:

• $BB_1=h$
• $BE=2cdot a$ — потому что $EO=OB=a$
• $angle EBB_1=90^{circ}$ — по свойствам правильной призмы

Таким образом, получается, что треугольник $BEB_1$ прямоугольный. По свойствам прямоугольного треугольника $$ EB_1=sqrt{BB_1^2+BE^2}=sqrt{h^2+4cdot a^2} $$ Если $h=a$, то тогда $$ EB_1=sqrt{5}cdot a $$ После аналогичных рассуждений получаем, что $FC_1=AD_1=BE_1=CF_1=DA_1=sqrt{h^2+4cdot a^2}$.

Находим $OF_1$

В треугольнике $FOF_1$:

• $FF_1=h$
• $FO=a$
• $angle OFF_1=90^{circ}$ — по свойствам правильной призмы

Таким образом, получается, что треугольник $FOF_1$ прямоугольный. По свойствам прямоугольного треугольника $$ OF_1=sqrt{FF_1^2+OF^2}=sqrt{h^2+a^2} $$ Если $h=a$, то тогда $$ OF_1=sqrt{2}cdot a $$ После аналогичных рассуждений получаем, что $OA_1=OB_1=OC_1=OD_1=OE_1=sqrt{h^2+a^2}$.

Находим $FE_1$

В треугольнике $FEE_1$:

• $EE_1=h$
• $FE=a$
• $angle FEE_1=90^{circ}$ — по свойствам правильной призмы

Таким образом, получается, что треугольник $FEE_1$ прямоугольный. По свойствам прямоугольного треугольника $$ FE_1=sqrt{FE^2+EE_1^2}=sqrt{h^2+a^2} $$ Если $h=a$, то тогда $$ FE_1=sqrt{2}cdot a $$ После аналогичных рассуждений получаем, что длины диагоналей остальных боковых граней призмы также равны $sqrt{h^2+a^2}$.