Стороны прямоугольного параллелепипеда
Egor Avva
Ученик
(112),
на голосовании
10 лет назад
Как найти стороны если известно что диагональ равна 20 см, а основание параллелепипеда квадратное. т. е. a=b.
L- диагональ, 2a^2+b^2=400 . как отсюда выразить стороны не понимаю подскажите пожалуйста.
Дополнен 10 лет назад
2a^2+c^2=400 (перепутал) и да параллелепипед явл. кубом
Голосование за лучший ответ
Прямоугольный параллелепипед является прямой призмой, в основании которой лежит квадрат или прямоугольник, таким образом, совокупность ребер прямоугольного параллелепипеда может представлять собой два или три разных параметра. Если же они все равны между собой, то можно с уверенностью сказать, что такой параллелепипед является кубом, и его ребро можно найти по формулам, приведенным в разделе «Ребро куба».
Ребро прямоугольного параллелепипеда можно найти, зная объем тела и другие ребра:
Также можно рассчитать ребро прямоугольного параллелепипеда через площадь боковой или полной поверхности, тоже зная остальные два ребра:
Как и в случае с кубом, внутри прямоугольного параллелепипеда можно провести диагональ, которая соединит противоположные вершины оснований. В прямоугольном треугольнике диагональ параллелепипеда D будет гипотенузой, а диагональ основания d и ребро a – катетами. Тогда боковое ребро параллелепипеда можно будет найти через теорему Пифагора.
Если дана диагональ параллелепипеда, но нужно найти ребро, не входящее во внутренний прямоугольный треугольник, а являющееся стороной основания, то формула придет к точно такому же виду.
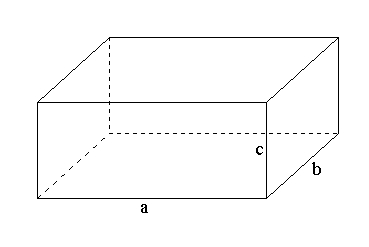
Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.
Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником.
Любой параллелепипед характеризуется 3 сторонами a, b и c (см. рисунок) и диагональю. Именно эти характеристики используются в формулах параллелепипеда при вычислении объема и площади.
Диагональ параллелепипеда – это отрезок, соединяющий противоположные вершины параллелепипеда.
Формула диагонали параллелепипеда
Диагональ d прямоугольного параллелепипеда можно получить, зная его стороны:
d2 = a2 + b2 + c2
Формула площади параллелепипеда
Площадь поверхности прямоугольного параллелепипеда можно получить, зная его стороны:
S = 2(ab + ac + bc)
Формула объема параллелепипеда
Объем прямоугольного параллелепипеда можно вычислить, зная его стороны:
V = abc
Параллелепипед
Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Читай статью, смотри вебинар и ты все про него будешь знать!
Параллелепипед — коротко о главном
Параллелепипед — это четырехугольная призма (многогранник с ( displaystyle 6) гранями), все грани которой — параллелограммы.
Прямой параллелепипед —это параллелепипед, у которого ( displaystyle 4) боковые грани — прямоугольники.
Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники
Куб — параллелепипед, у которого все грани квадраты.
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства параллелепипеда
- Противолежащие грани параллелепипеда параллельны и равны.
- Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через точку пересечения диагоналей (центр параллелепипеда), делится ею пополам.
- Все диагонали прямоугольного параллелепипеда равны между собой и равны сумме квадратов его измерений. ( displaystyle ^>=>+^>+^>).
Параллелепипед — подробнее
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.
Далее смотри на картинки, запоминай и не путай!
Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
Свойства параллелепипеда
- Всеграни параллелепипеда – параллелограммы.
- Противоположные грани параллелепипеда параллельны и равны.
Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные.
Геометрические фигуры. Прямоугольный параллелепипед.
Прямоугольный параллелепипед — прямой параллелепипед с прямоугольником в основании. У прямоугольного параллелепипеда каждая из шести граней является прямоугольником.
Примерами прямоугольного параллелепипеда являются спортивный зал, коробок спичек или системный блок компьютера.
Формулы прямоугольного параллелепипеда.
Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба являются равными квадратами.
Обозначим длину ребра куба как n, тогда площадь 1-ой грани:
Площадь поверхности куба:
У прямоугольного параллелепипеда есть еще одно измерение – объем параллелепипеда (обозначается как V).
Прямоугольники, которые составляют поверхность параллелепипеда, являются гранями параллелепипеда.
Прямоугольный параллелепипед определяют 3-мя измерениями:
Высота (обозначают как h) равняется длине ребра № 1.
Длина (обозначают как m) равняется длине ребра № 2.
Ширина (обозначают как n) равняется длине ребра № 3.
Площадь всей поверхности параллелепипеда обозначают как S:
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$ — высота(она же боковое ребро);
$P_$ — периметр основания;
$S_$ — площадь основания;
$S_$ — площадь боковой поверхности;
$S_$ — площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_=P_·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
Дополнительные сведения, которые пригодятся для решения задач:
$а$ — длина стороны.
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/$, где $h_a$ — высота, проведенная к стороне $а$.
- $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√
$, где $р$ — это полупериметр $p=/$.
- $S=p·r$, где $r$ — радиус вписанной окружности.
- $S=/$, где $R$ — радиус описанной окружности.
- Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S=/$, где $а$ — длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны. - Ромб.
$S=/$, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами. - Трапеция.
$S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции. - Квадрат.
$S=a^2$, где $а$ — сторона квадрата.
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ – длина;
$b$ – ширина;
$с$ – высота(она же боковое ребро);
$P_{осн}$ – периметр основания;
$S_{осн}$ – площадь основания;
$S_{бок}$ – площадь боковой поверхности;
$S_{п.п}$ – площадь полной поверхности;
$V$ – объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ – длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ – высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ – это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ – радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ – радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ – катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ – длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции. - Квадрат.
$S=a^2$, где $а$ – сторона квадрата.
Пример:
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ – стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$






