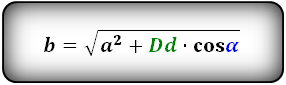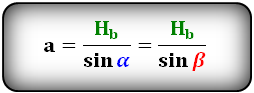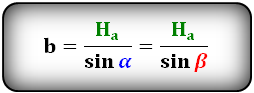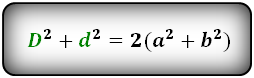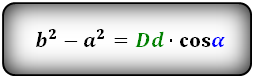Как найти сторону параллелограмма если известен радиус - Сайт, где вы сможете решить свои вопросы

Как найти длину одной из сторон параллелограмма?

Чтобы найти сторону параллелограмма, необходимо наличие некоторых других значений, которые бы были известны. Далее попросту использовать одну из подходящих формул.

Например, по теореме косинусов, это формулы сторон через диагонали и находящийся между ними угол:

Другим решением, являются формулы, где стороны рассчитываются по диагонали и одной из известной стороны:

Вот еще формулы сторон параллелепипеда, через вторую сторону, диагонали и косинус угла:

Стоит напомнить и про формулы длин сторон, через высоту и синус угла:

Так же длину стороны параллелограмма, можно определить если известны площадь и высота:

Как видим, вариантов расчета высоты параллелограмма достаточно много и хотелось напомнить основные характеристики этой геометрической фигуры:

Во первых, параллелограммом называется четырехугольник, имеющий параллельно расположенные противоположные стороны , т. е. находящиеся на параллельных прямых. Квадраты, прямоугольники и ромбы, также являются параллелограммами.

система выбрала этот ответ лучшим

Для нахождения стороны параллелограмма есть более десятка разных формул (они перечислены в ответе автора Бульбозавр), но для решения задач на эту тему, далеко не всегда их можно применить.

На мой взгляд лучше всего разобрать несколько примеров и на практике увидеть, как находить сторону этой фигуры – в наших случаях с помощью уравнений.

Пример 1

Нужно найти стороны параллелограмма, если одна из сторон больше другой в два раза а периметр равен 30 см.

Даже не нужно чертить рисунок, а просто составить уравнение и решить его

периметр(30см) = 2(х+2х) откуда х=5см, следовательно одна сторона равна 5см, другая – 10см.

Пример 2

АВСД – параллелограмм, нужно найти его стороны если – ВМ перпендикуляр к АС, АМ=6см, МС=15см, ВС больше АВ на 6 см

Для решения этой задачи сначала рассматриваем два прямоугольных треугольника АВМ и ВСМ у которых общий катет h.

Согласно Пифагору

h*h=a*a-6*6=b*b-15*15 откуда b*b-a*a=(b-a)(b+a)=225-36=189

по условию задачи b-a=7 тогда b+a=189/7=27

решив эту простенькую систему уравнений найдем стороны a=10см b=17cм

Alexsandr82
[21.4K]

5 лет назад

Есть еще несколько формул которые будут скорее вспомогательными при решении задач по нахождению стороны паралелограмма но тем не менее их тоже нужно знать. Например одну из сторон паралеллограмма можно найти если известна вторая сторона и периметр фигуры по формуле:

Р = 2(а+b), тогда а = (Р/2 – b), или b = (P/2 – a), где Р – периметр, а и b – стороны.

Также можно найти сторону паралеллограмма зная его площадь и высоту опущенную на искомую сторону:

S = a*H1 = b*H2, тогда а = S/H1 или b = S/H2, где S – площадь, а – меньшая сторона паралелограмма, b – большая сторона, Н1 – высота построенная к меньшей стороне, Н2 – сторна построенная к большей стороне паралеллограмма.

Vector 60
[121]

8 месяцев назад

Существует несколько формул для вычисления сторон параллелограмма (a и b).

1) Для нахождения сторон параллелограмма можно воспользоваться длиной диагоналей, а также величиной углов между диагоналями. Формулы будут такими:

2) Если известна одна из сторон и диагонали, то другую сторону можно найти так:

3) Если известна высота и величина одного из углов, то стороны параллелограмма можно найти по таким формулам:

4) Еще можно использовать значение площади и высоты:

Stasy12
[41.5K]

более года назад

Формул, конечно много, с помощью которых можно найти сторону параллелограмма.

Например можно найти стороны паралелограмма, зная размеры диагоналей и угла между ними(формула 1и 2)

Зная длины диагоналей и одну из сторон, легко можно найти вторую(формулы 3 и 4)

Через высоту, которая опущена на сторону и угол между сторонами(формулы 5 и 6)

Зная площадь и высоту, которая опущена на

заданную сторону можно найти длину стороны(формулы 7 и 8).

Знаете ответ?

Источник

Свойства параллелограмма:

1. Противоположные стороны равны и параллельны

2. Противоположные углы равны

3. Точка пересечения диагоналей, делит их пополам

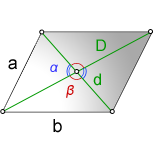
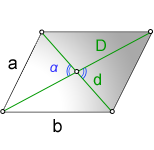
1. Формулы длины сторон через диагонали и угол между ними.

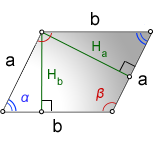
a, b – стороны параллелограмма

D – большая диагональ

d – меньшая диагональ

α, β – углы между диагоналями

Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):

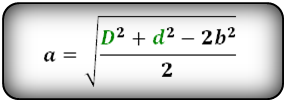
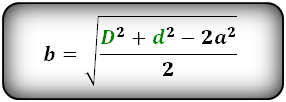
Формулы сторон параллелограмма через диагонали и сторону, (a, b):

Формулы сторон параллелограмма , (a, b):

2. Формулы длины сторон параллелограмма через высоту.

a, b – стороны параллелограмма

H_b – высота на сторону b

Ha – высота на сторону a

α, β – углы параллелограмма

Формулы сторон параллелограмма через высоту, (a, b):

3. Дополнительные, интересные формулы параллелограмма:

a, b – стороны параллелограмма

D – большая диагональ

d – меньшая диагональ

α – острый угол между диагоналями

Формула суммы квадратов диагоналей:

Формула разности квадратов сторон:

Формулы площади параллелограмма

Формула периметра параллелограмма

Все формулы по геометрии

Подробности

Опубликовано: 31 октября 2011

Обновлено: 13 августа 2021

Источник

В параллелограмм вписана окружность

Если в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме?

Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны.

Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

Радиус вписанной в ромб окружности можно найти по формуле

где S — площадь ромба, p — его полупериметр;

или как половину высоты ромба

1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см.

Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны.

2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см.

Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты:

3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.

Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).

Пусть ABCD — ромб, AC=6 см, BD=8 см.

Рассмотрим треугольник AOB.

По теореме Пифагора

полупериметр — p=2a=2∙AB=25=10 см.

Следовательно, радиус вписанной окружности равен

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c – стороны треугольника

p – полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a – сторона треугольника

r – радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a – равные стороны равнобедренного треугольника

b – сторона ( основание)

α – угол при основании

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a – равные стороны равнобедренного треугольника

b – сторона ( основание)

h – высота

О – центр вписанной окружности

r – радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

Треугольник
Выпуклый, правильный многоугольник
Квадрат
Равнобедренная трапеция
Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

В любой треугольник может быть вписана окружность, причем только один раз.
Центр вписанной окружности — точка пересечения биссектрис треугольника.
Вписанная окружность касается всех сторон треугольника.
Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Центр окружности вписанной в треугольник равноудален от всех сторон.

Точка касания — это точка, в которой соприкасается
окружность и любая из сторон треугольника.

От центра вписанной окружности можно провести
перпендикуляры к любой точке касания.

Вписанная в треугольник окружность делит стороны
треугольника на 3 пары равных отрезков.

Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.

В четырехугольник

Не во всякий четырехугольник можно вписать окружность.
Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито).
Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
Точка пересечения биссектрис — это центр вписанной окружности.
Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника.
Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c+d)cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Точка касания вписанной окружности, которая лежит на любой из сторон,
равноудалены от этой конца и начала этой стороны, то есть от его вершин.

Примеры вписанной окружности

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
Любой параллелограмм можно вписать в окружность. Неверное утверждение.
В любой четырехугольник можно вписать окружность. Неверное утверждение.
В любой ромб можно вписать окружность. Верное утверждение.
Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение.
Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение.
Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

[spoiler title=”источники:”]

http://www-formula.ru/2011-09-24-00-40-48

http://colibrus.ru/vpisannaya-okruzhnost/

[/spoiler]

Источник

Параллелограммом называют четырёхугольный многоугольник, две соседние стороны которого равны и
параллельны противоположным. Помимо этого, есть ещё несколько важных условий определения фигуры как
параллелограмма:

В месте пересечения диагонали делятся пополам, а точка, в которой пересекаются диагонали,
является одновременно центром этих двух отрезков. При этом она всегда лежит внутри фигуры.
Любая диагональ данного четырёхугольника разделяет его на одинаковые треугольники, так как
проходит из одной вершины к противоположной, то есть по центру четырёхугольника.
Сумма квадратов сторон равна сумме квадратов диагоналей.
Углы фигуры, расположенные друг напротив друга, попарно равны. Это условие вытекает из
утверждения, что параллельные стороны фигуры равны.
Сумма двух односторонних углов равна 180°. Это условие напрямую связано с теоремой о двух
параллельных прямых и секущей. И действительно, если рассматривать две противоположные и третью
между ними стороны параллелограмма как две параллельные прямые и секущую, то можно заметить, что
углы, принадлежащие одной стороне, будут соответствовать односторонним углам, сумма которых,
согласно теореме, равна 180°.

Только при выполнении всех условий четырёхугольный многоугольник будет считаться
параллелограммом.

Длинная сторона параллелограмма через две диагонали и
острый угол между ними
Длинная сторона параллелограмма через две диагонали и тупой
угол между ними
Короткая сторона параллелограмма через две диагонали и
острый угол между ними
Короткая сторона параллелограмма через две диагонали и
тупой угол между ними
Сторона параллелограмма через две диагонали и другую
известную сторону
Сторона параллелограмма через высоту и синус угла
Сторона параллелограмма через площадь и высоту

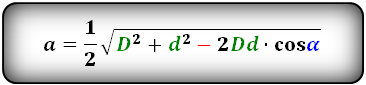
Нахождение длинной стороны через две диагонали и острый угол между ними

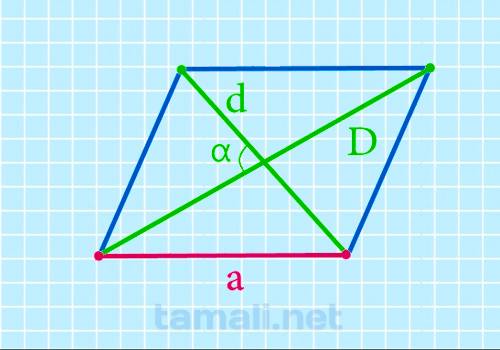
Длинную сторону параллелограмма можно найти, зная обе диагонали и острый угол между ними, по
формуле:

a = (√(D² + d² — 2 (D * d) * cosα)) / 2

где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.

Цифр после
запятой:

Результат в:

Пример. Допустим, дан параллелограмм, у которого диагонали 7 и 4 см, а угол между
ними 68º. Тогда, согласно формуле, сторона будет равна: a = (√(7² + 4² — 2 (7 * 4) * cos68º)) / 2 = 3,317 см. Ответ:
3,317 см.

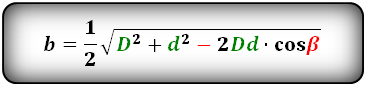
Нахождение короткой стороны через две диагонали и острый угол между ними

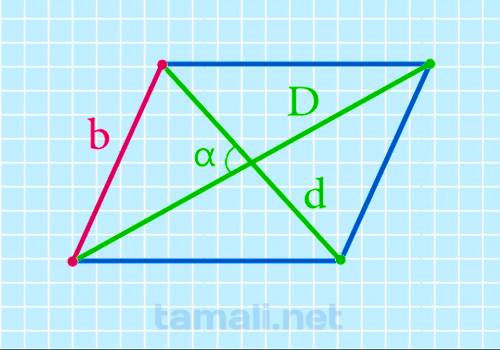
Можно вычислить и короткую сторону по формуле:

b = (√(D² + d² + 2 (D * d) * cosα)) / 2

где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.

Цифр после
запятой:

Результат в:

Пример. Теперь необходимо найти другую сторону параллелограмма. Данные останутся те
же, что и в прошлой задаче, но в уравнении поменяется знак, так как по отношению к углу поменялась
сторона, которую надо найти. Сторона b будет равна: b = (√(7² + 4² + 2 (7 * 4) * cos68º)) / 2 = 4.64.
Ответ: 4,64 см.

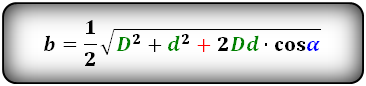
Нахождение длинной стороны через две диагонали и тупой угол между ними

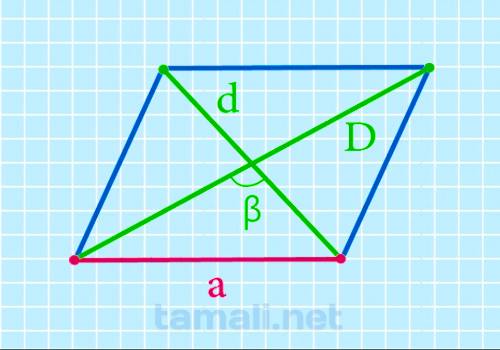
Стороны параллелограмма можно найти, зная диагонали и тупой угол между ними. Для этого нужно
использовать следующую формулу:

a = (√(D² + d² + 2 (D * d) * cosβ)) / 2

где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.

Цифр после
запятой:

Результат в:

Пример. Рассмотрим нахождение сторон всё того же параллелограмма с диагоналями 7 и 4
см. Однако на этот раз возьмём между диагоналями другой угол: β=112º. В таком случае для стороны a
минус меняется на плюс, а сама сторона равна: a = (√(7² + 4² + 2 (7 * 4) * cos112º)) / 2 = 3.914

Нахождение короткой стороны через две диагонали и тупой угол между ними

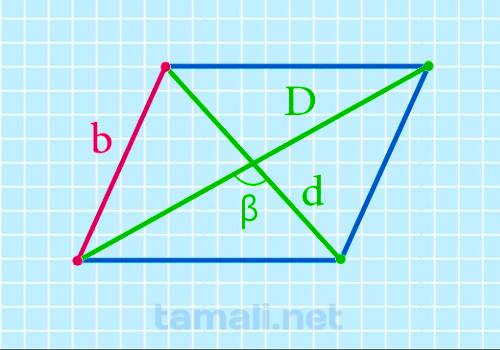
Аналогично можно найти и короткую сторону, зная диагонали и тупой угол между ними:

b = (√(D² + d² — 2 (D * d) * cosβ)) / 2

где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.

Цифр после
запятой:

Результат в:

Пример. Для стороны b так же изменится знак в формуле, но наоборот: плюс на минус. Тогда
получается: b = (√(7² + 4² — 2 (7 * 4) * cos112)) / 2 = 4,64 см. Ответ совпал с ответом второй
задачи, все опять решено верно, а сторона в воображаемом параллелограмме действительно равна 4,64
см.

Нахождение стороны параллелограмма через диагонали и другую сторону

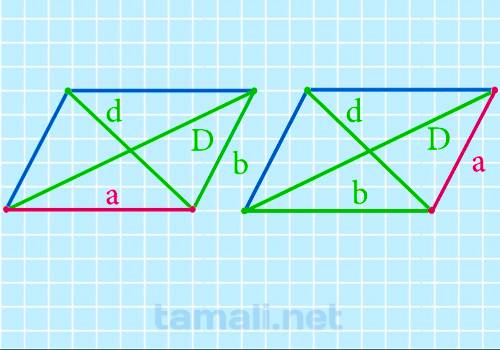
Как и в случае с прошлыми пунктами, существуют формула, которая позволяет найти сторону
параллелограмма с использованием диагоналей и известной стороны. Вот она:

a = √(D² + d² — 2b² / 2)

где D, d — диагонали, b — сторона.

Цифр после
запятой:

Результат в:

Выводится данная формулы из первого следствия теоремы косинусов.

Пример. Используем для следующих задач другой параллелограмм. Эта фигура будет с
диагоналями 9 и 5 см и стороной 6 см. Тогда другая сторона данного параллелограмма равна: a = √(9² + 5² — 2 * 6² / 2) = 4,1 см. Ответ: 4,1 см.

Для проверки ответа можем решить обратную задачу, при которой нам не известна сторона b, но известна
сторона a = 4,1 см. По обратной формуле получается b = √(9² + 5² — 2 * 4,1² / 2) = 6 см. Ответ
совпадает с изначальными данными первой задачи. А значит и этот воображаемый параллелограмм
действительно существует.

Нахождение стороны через синус угла и высоту

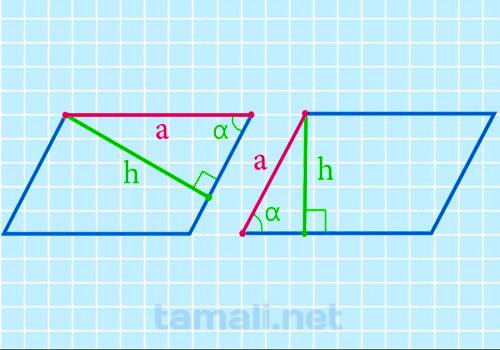
Высота – это отрезок, опущенный перпендикулярно из вершины фигуры на противоположную сторону. Есть
несколько интересных свойств у неё. Например, высоты, проведенные из острых углов, будут всегда
лежать вне фигуры, в то время как высоты из тупых углов всегда лежат внутри. Если из одного угла
опустить две высоты, то между ними образуется угол, равный смежному углу параллелограмма. Равными
будут те высоты, что заключены между параллельными сторонами четырёхугольника. Найти сторону
параллелограмма через эту величину достаточно просто, по формуле:

a = h / sinα

где: h — высота параллелограмма, sin α — угол.

Цифр после
запятой:

Результат в:

Стоит заметить, что высота должна быть опущена не к искомой стороне, а к соседней. При этом для
формулы сойдет синус любого известного угла параллелограмма.

Пример. Найти сторону параллелограмма, если высота, опущенная на соседнюю сторону
равна 10 см, а острый угол — 30º. Решение: a=10 / 0,5 = 20 см

Нахождение стороны через площадь и высоту

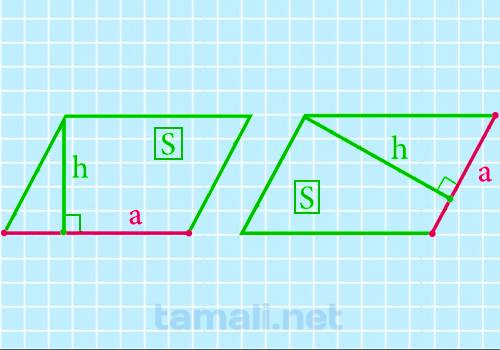
Более подробно о площади и высоте параллелограмма рассказано в пунктах выше. В этом достаточно легко
вывести единственную формулу, по которой можно найти сторону. Если площадь является произведением
стороны на высоту, то сторона будет равна отношению площади к высоте:

a = S / h

где S — площадь параллелограмма, h — высота.

Цифр после
запятой:

Результат в:

Причем не имеет значения, к какой стороне опущена высота: к искомой или соседней.

Пример. Найти сторону параллелограмма, если его площадь равна 20 см, а высота,
опущенная на одну из сторон — 5 см. Решение: a = 20 / 5 = 4 см.

Фигура кажется сложной для восприятия из-за того, что её нельзя постоянно наблюдать где-то в
повседневной жизни. Однако всё становится проще, если вспомнить, что есть более известные широкой
публике частные случаи параллелограмма. Их-то человек обычно наблюдает ежедневно. Это ромб,
прямоугольник и квадрат. Причем последний, хоть и наиболее известен, является и наиболее
интересным.

Ромб считается частным случаем, потому что представляет собой параллелограмм, диагонали которого в
точке пересечения образуют прямой угол. Прямоугольник является частным случаем, потому что это
параллелограмм, у которого все углы прямые. У квадрата же положение ещё интереснее, так как его
можно назвать не только частным случаем параллелограмма, но и прямоугольника, и ромба. Квадрат – это
комбо трёх предыдущих определений. Можно даже сказать, что квадрат одновременно является особенным
случаем и для параллелограмма, и для прямоугольника, и для ромба. Все его стороны равны,
противоположные стороны параллельны. Все углы являются прямыми, даже образующиеся при пересечении
диагоналей, которые к тому же делятся пополам в точке пересечения.

Источник

Радиус вписанной в ромб окружности можно найти по формуле

$[r = frac{S}{p},]$