Как найти сторону правильного четырехугольника зная диагональ

Определение правильного многоугольника

Правильный многоугольник – это выпуклый многоугольник, у которого равны все стороны и углы.

Признаки правильного n-угольника

• a1 = a2 = a3 = … an-1 = an
• α1 = α2 = α3 = … αn-1 = αn

Примечание: n – количество сторон/углов фигуры.

Элементы правильного многоугольника

Для рисунка выше:

• a – сторона/ребро;
• α – угол между смежными сторонами;
• O – центр фигуры/масс (совпадает с центрами описанной и вписанной окружностей);
• β – центральный угол описанной окружности, опирающийся на сторону многоугольника.

Диагонали n — угольника

Фигура	Рисунок	Описание
Диагональ многоугольника		Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали n – угольника, выходящие из одной вершины		Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Все диагонали n – угольника		Число диагоналейn – угольника равно

Диагональ многоугольника

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника

Диагонали n – угольника, выходящие из одной вершины

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника

Все диагонали n – угольника

Число диагоналей n – угольника равно

Внешний угол многоугольника

Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).

Рис.1

Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).

Рис.2

Замечание. Мы рассматриваем только выпуклые многоугольники выпуклые многоугольники .

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению  180°  и количеству сторон без двух.

s = 2d(n — 2),

где  s  — это сумма углов,  2d  — два прямых угла (то есть  2 · 90 = 180°),  а  n  — количество сторон.

Если мы проведём из вершины  A  многоугольника  ABCDEF  все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна  180°  (2d),  то сумма углов всех треугольников будет равна произведению  2d  на их количество:

s = 2d(n — 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна  360°  (или  4d).

s = 4d,

где  s  — это сумма внешних углов,  4d  — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна  180°  (2d),  так как они являются смежными углами. Например,  ∠1  и  ∠2:

Следовательно, если многоугольник имеет  n  сторон (и  n  вершин), то сумма внешних и внутренних углов при всех  n  вершинах будет равна  2dn.  Чтобы из этой суммы  2dn  получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть  2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.

Виды правильных многоугольников

1. Правильный (равносторонний) треугольник
2. Правильный четырехугольник (квадрат)
3. Правильный пяти-, шести-, n-угольник

Основные свойства правильного многоугольника

• Все стороны равны:
  a1 = a2 = a3 = … = an-1 = an2. Все углы равны:
  α1 = α2 = α3 = … = αn-1 = αn3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O4. Сумма всех углов n-угольника равна:

180° · (n — 2)

• Сумма всех внешних углов n-угольника равна 360°:

β1 + β2 + β3 + … + βn-1 + βn = 360°

• Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:

• В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:

• Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O

Свойство 1

Внутренние углы в правильном многоугольнике (α) равны между собой и могут быть рассчитаны по формуле:

где n – число сторон фигуры.

Свойство 2

Сумма всех углов правильного n-угольника равняется: 180° · (n-2).

Свойство 3

Количество диагоналей (Dn) правильного n-угольника зависит от количества его сторон (n) и определяется следующим образом:

Свойство 4

В любой правильный многоугольник можно вписать круг и описать окружность около него, причем их центры будут совпадать, в том числе, с центром самого многоугольника.

В качестве примера на рисунке ниже изображен правильный шестиугольник (гексагон) с центром в точке O.

Площадь (S) образованного окружностями кольца вычисляется через длину стороны (a) фигуры по формуле:

Между радиусами вписанной (r) и описанной (R) окружностей существует зависимость:

Свойство 5

Зная длину стороны (a) правильного многоугольника можно рассчитать следующие, относящиеся к нему величины:

• Площадь (S):

• Периметр (P):
• Радиус описанной окружности (R):

• Радиус вписанной окружности (r):

Свойство 6

Площадь (S) правильного многоугольника можно выразить через радиус описанной/вписанной окружности:

Доказательства свойств углов многоугольника

Теорема 1. В любом треугольнике сумма углов равна 180°.

Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).

Рис.3

Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.

Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).

Рис.4

Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.

Замечание. Теорема 1 является следствием теоремы 2.

Теорема 3. Сумма углов  – угольникаn равна

Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).

Рис.5

Получим n треугольников:

OA1A2,  OA2A3,  …  OAnA1

Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна

что и требовалось доказать.

Теорема 4. Сумма внешних углов  – угольникаn , взятых по одному у каждой вершины, равна 360°.

Доказательство. Рассмотрим рисунок 6.

Рис.6

В соответствии рисунком 6 справедливы равенства

Теорема доказана.

Правильный n-угольник — формулы

Формулы длины стороны правильного n-угольника

• Формула стороны правильного n-угольника через радиус вписанной окружности:

• Формула стороны правильного n-угольника через радиус описанной окружности:

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:

Формулы площади правильного n-угольника

• Формула площади n-угольника через длину стороны:

• Формула площади n-угольника через радиус вписанной окружности:

• Формула площади n-угольника через радиус описанной окружности:

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:

Рис.3

Формулы правильного треугольника:

• Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

• Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

• Формула радиуса вписанной окружности правильного треугольника через длину стороны:

• Формула радиуса описанной окружности правильного треугольника через длину стороны:

• Формула площади правильного треугольника через длину стороны:

• Формула площади правильного треугольника через радиус вписанной окружности:

S = r2 3√3

• Формула площади правильного треугольника через радиус описанной окружности:

• Угол между сторонами правильного треугольника:

α = 60°

Рис.4

Формулы правильного четырехугольника:

• Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

• Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

• Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:

• Формула радиуса описанной окружности правильного четырехугольника через длину стороны:

• Формула площади правильного четырехугольника через длину стороны:

S = a2

• Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r2

• Формула площади правильного четырехугольника через радиус описанной окружности:

S =  2 R2

• Угол между сторонами правильного четырехугольника:

α = 90°

Формулы правильного шестиугольника:

Формула стороны правильного шестиугольника через радиус вписанной окружности:

Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:

Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

Формула площади правильного шестиугольника через длину стороны:

Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r2 2√3

Формула площади правильного шестиугольника через радиус описанной окружности:

8. Угол между сторонами правильного шестиугольника:

α = 120°

Формулы правильного восьмиугольника:

Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 — 1)

Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 — √2

Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:

Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:

Формула площади правильного восьмиугольника через длину стороны:

S = a2 2(√2 + 1)

Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r2 8(√2 — 1)

Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R2 2√2

Угол между сторонами правильного восьмиугольника:

α = 135°

Сторона правильного многоугольника через радиус описанной вокруг него окружности

Сторону правильного многоугольника через радиус описанной вокруг него окружности можно найти по формуле

Где:

a – длина его стороны;

R – радиус описанной окружности;

n – число сторон многоугольника.

Формула стороны правильного многоугольника

Шаг 1

Рассмотрим правильный многоугольник А1А2А3…Аn.

Пусть его сторона будет равна a.

Опишем вокруг этого многоугольника окружность с центром в точке О и радиусом R.

Вывод формулы стороны правильного многоугольника.

Шаг 2

Соединим точку О с его вершинами. А1А2А3…Аn.

Рассмотрим треугольник ОА1А2.

Рассматриваемый треугольник будет равнобедренным, так как его стороны А1О и А2О – радиусы описанной окружности.

Проведем в треугольнике А1ОА2 высоту ОК.

Так как треугольник А1ОА2 равнобедренный, то высота будет медианой:

Вывод формулы стороны правильного многоугольника.

Шаг 3

Рассмотрим треугольник А1КО.

Этот треугольник прямоугольный, так как ОК – высота по построению.

Так как точка О – центр правильного многоугольника, то отрезки АnO являются биссектрисами углов этого многоугольника.

Таким образом, если углы многоугольника обозначим буквой α, то угол ОА1К будет равен:

По свойству углов правильного многоугольника, каждый угол равен:

Тогда угол ОА1К будет равен:

Из определения косинуса угла получим:

Отсюда:

Подставим в формулу значения, полученные выше и на шаге 2:

Умножим обе части уравнения на 2:

Воспользуемся формулами приведения

Так как А1О является радиусом описанной окружности, то сторона правильного многоугольника может быть найдена по формуле:

Вывод формулы стороны правильного многоугольника.

Как найти сторону правильного многоугольника

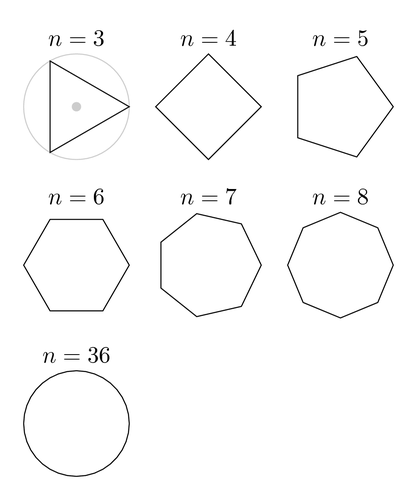
Фигура, образованная более чем из двух линий, замыкающихся между собой, называется многоугольником. Каждый многоугольник имеет вершины и стороны. Любой из них может быть правильным или неправильным.

Инструкция

Правильным многоугольником называется фигура, у которой все стороны равны. Так, например, равносторонний треугольник представляет собой правильный многоугольник, состоящий из трех замкнутых линий. В данном случае, все его углы равны 60 °. Его стороны между собой равны, но не параллельны друг другу. Таким же свойством обладают и другие многоугольники, однако, углы у них имеют другие величины. Единственный из правильных многоугольников, у которого стороны не только равны, но и попарно параллельны – квадрат.Если в задаче дан равносторонний треугольник с площадью S, то его неизвестную сторону можно найти через углы и стороны. Прежде всего, найдите высоту треугольника h, перпендикулярную к его основанию:h=a*sinα=a√3/2, где α=60° – один из углов, прилежащих к основанию треугольника.Руководствуясь этими соображениями, преобразуйте формулу для нахождения площади таким образом, чтобы по ней можно было вычислить длину стороны:S=1/2a*a√3/2=a^2*√3/4Отсюда следует, что сторона a равна:a=2√S/√√3

Сторону правильного четырехугольника найдите, пользуясь несколько иным способом. Если он представляет собой квадрат, в качестве первоначальных данных используйте его площадь или диагональ:S=a^2Следовательно, сторона a равна:a=√SКроме того, если дана диагональ, то сторону можно вычислить и по другой формуле:a=d/√2

В большинстве случаев сторону правильного многоугольника можно определить, зная радиус вписанной в него или описанной вокруг него окружности. Известно, что имеется взаимосвязь между стороной треугольника и радиусом окружности, описанной вокруг этой фигуры:a3=R√3, где R – радиус описанной окружностиЕсли окружность вписана в треугольник, то формула приобретает другой вид:a3=2r√3, где r – радиус вписанной окружностиУ правильного шестиугольника формула для нахождения стороны при известном радиусе описанной (R) или вписанной (r) окружностей выглядит следующим образом:a6=R=2r√3/3Из этих примеров можно сделать вывод, что для всякого произвольного n-угольника формула для нахождения стороны в общем виде выглядит следующим образом:a=2Rsin(α/2)=2rtg(α/2)

Источники:

• сторона правильного многоугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла.
Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой.
Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами,
квадрат — это особенный случай прямоугольника.

Через диагональ и угол между диагональю и стороной

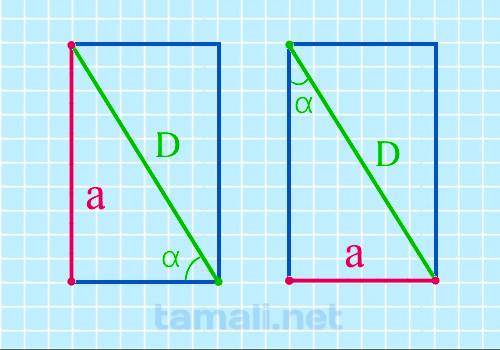
Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол
средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно
воспользоваться следующей формулой:

a = d * sinα

где d — это диагональ, а, b — одна из сторон фигуры.

Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой
стороной — 60º.

Решение.
D = 16, β = 60º, b = ?
b = 16 cos 60º
b = 16 * 0.5 = 8 см.

Через его площадь и известную сторону

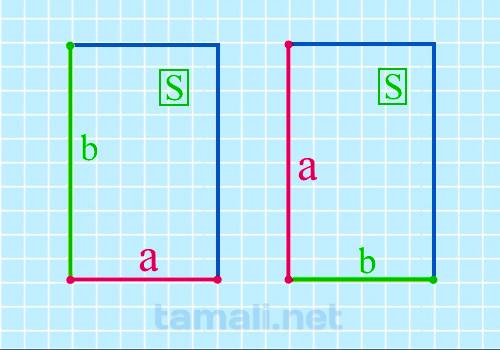
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно

a = S / b

где S — площадь прямоугольника, b — известная сторона.

Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем
известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.

Через диагональ и известную сторону

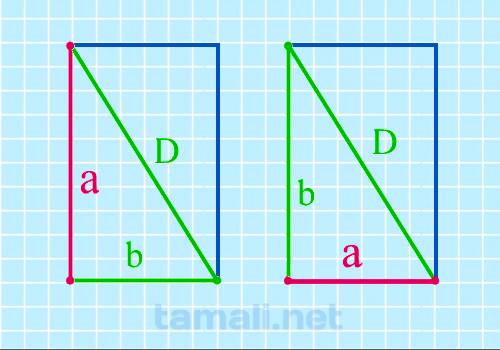
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.
Диагональ
— это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них
разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а
две соседние стороны — остальные стороны треугольника. Отсюда :

a = √(d² — b²)

где d — диагональ, а, b — стороны.

Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.

Решение.
D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см.
​

Через диагональ и угол между диагоналями

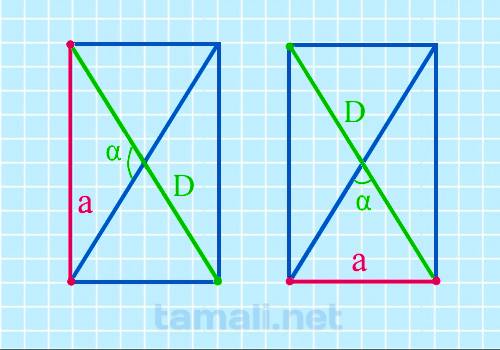
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать
сторону прямоугольника, зная следующую формулу:

a = D • sin(α/2)

где D — диагональ, α — угол между диагоналями.

Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти
сторону.

Решение.
a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.

Через периметр и другую известную сторону

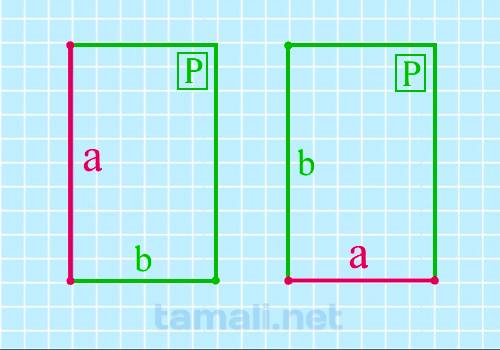
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра
для получения длины. P = 2 (a + b).

a = (P — 2b) / 2

где P — периметр прямоугольника, b — другая известная сторона.

Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4).Вычислив,
получим 12 см.

Другие примеры по решению задач на прямоугольник с использованием длины и ширины

1. Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
   Результат: P
   прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов
2. Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3
   м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы
   преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см.
   Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см².
3. Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти
   периметр прямоугольника. Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17,
   используем теорему Пифагора и составим уравнение: AB² +AD² =BD².
   Получаем: х² +(х+7)² =17² ⇒ х² +х² +14х+49=289; 2х² +14х-240=0; х² +7х-120=0,
   отсюда по теореме Виета х1 =-15; х2 =8.Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника: P = 2∙ (AB+AD); P = 2∙ (8+15); P = 46 см.
   Ответ: 46 см.

Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены
ниже.

• Прямоугольник — это четырехугольник.
• Противоположные стороны прямоугольника являются равными и параллельны друг другу.
• Внутренний угол прямоугольника при каждой вершине равен 90°.
• Сумма внутренних углов равна 360°.
• Диагонали пересекаются друг с другом.
• Длина диагоналей равна.
• Длина диагоналей может быть получена с помощью теоремы Пифагора. Длина диагонали со сторонами a
  и b равна, диагональ = ( a2 + b2).
• Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
• Все прямоугольники являются параллелограммами, но все параллелограммы не являются
  прямоугольниками.