Как найти сторону правильного двенадцатиугольника

Длина стороны правильного многоугольника

Определение длины стороны правильного многоугольника по радиусу вписанной окружности

От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».

Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

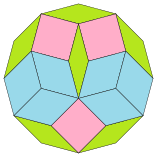
Впишите в окружность правильный двенадцатиугольник

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Площадь правильного двенадцатиугольника ⁠

Какие пра­виль­ные много­уголь­ники, впи­сан­ные в еди­нич­ную окруж­ность, имеют раци­о­наль­ную площадь? Ока­зы­ва­ется, таких всего два — квад­рат и пра­виль­ный две­на­дца­ти­уголь­ник.

Одно из кра­си­вых дока­за­тельств того, что площадь две­на­дца­ти­уголь­ника равна трём квад­ра­там ради­уса опи­сан­ной окруж­но­сти, при­над­лежит венгер­скому матема­тику Йожефу Кюршаку.

Чет­вер­тинка две­на­дца­ти­уголь­ника раз­би­ва­ется на пра­виль­ные тре­уголь­ники и рав­но­бед­рен­ные с углами $15^circ$, $15^circ$ и $150^circ$. После пере­кладки полу­ча­ется фигура, рав­ная трём чет­вер­тям квад­рата со сто­ро­ной, рав­ной диаметру опи­сан­ной около две­на­дца­ти­уголь­ника окруж­но­сти.

Если же известна длина сто­роны две­на­дца­ти­уголь­ника, то вычис­лить его площадь поз­во­ляет раз­би­е­ние на 6 квад­ра­тов, 6 рав­но­сто­рон­них тре­уголь­ни­ков между ними и цен­траль­ный шести­уголь­ник.

Если правильный двенадцатиугольник вписан в окружность радиусом R, то его сторона равна?

Геометрия | 5 — 9 классы

Если правильный двенадцатиугольник вписан в окружность радиусом R, то его сторона равна?

Там вот такая формула : R составляет S = (n / 2) * R ^ 2 * sin(2pi / n).

Просто подставь всё и сделано).

Радиус окружности равен 12 см?

Радиус окружности равен 12 см.

Найдите сторону вписанного в эту окружность правильного 1) шестиугольника 2) двенадцатиугольника.

Докажите, что если хорда перпендикулярна радиусу окружности и делит его пополам, то она равна стороне правильного треуголбника, вписанного в эту окружность?

Докажите, что если хорда перпендикулярна радиусу окружности и делит его пополам, то она равна стороне правильного треуголбника, вписанного в эту окружность.

В окружность вписан правильный треугольник?

В окружность вписан правильный треугольник.

В него вписана окружность, в которую вписан квадрат.

Найдите радиус большей окружности, если сторона квадрата равна 1 см.

В правильный шестиугольник со стороной равной a вписана окружность ?

В правильный шестиугольник со стороной равной a вписана окружность .

Найдите радиус этой окружности.

В правильный треугольник со стороной а вписана окружность, найдите радиус?

В правильный треугольник со стороной а вписана окружность, найдите радиус.

ПОМОГИТЕ ПОЖАЛУЙСТА?

В ОКРУЖНОСТЬ ВПИСАН ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК, СТОРОНА КОТОРОГО РАВНА 5.

НАЙДИТЕ ПЕРИМЕТР И ПЛОЩАДЬ ТРЕУГОЛЬНИКА, РАДИУС ОПИСАННОЙ И РАДИУС ВПИСАННОЙ ОКРУЖНОСТЕЙ.

В окружность вписан правильный шестиугольник?

В окружность вписан правильный шестиугольник.

В него вписана окружность, в которую вписан правильный треугольник.

Найдите радиус большей окружности, если сторона треугольника равна 1 см.

Помогите пожалуйста?

Найдите радиус окружности, вписанной в правильный треугольник со стороной 4 см.

Правильный треугольник со стороной см вписан в окружность?

Правильный треугольник со стороной см вписан в окружность.

Найдите радиус этой окружности.

Найти сходящие из одной вершины диагонали правильного двенадцатиугольника, вписанного в окружность с радиусом 8см?

Найти сходящие из одной вершины диагонали правильного двенадцатиугольника, вписанного в окружность с радиусом 8см.

Вы находитесь на странице вопроса Если правильный двенадцатиугольник вписан в окружность радиусом R, то его сторона равна? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

1)Состав им пропорцию AB / CB = CB / DB→AB / 10 = 10 / 5→AB = 20 АD = AB — DB = 20 — 5 = 15.

Пусть в ΔАВС вписана окружность. Е, К. М — точки касания окружности и сторон треугольника. По свойству отрезков касательных к окружности, проведенных из одной точки : АЕ = АМ = 20см, ВМ = ВК = 14см, тогда СК = СЕ = 30 — 14 = 16см. Значит, стороны..

Справедливо равенство под буквой А. Квадрат стороны в квадрате = сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

1) рк = мк — мр 1см = 10мм, значит мк = 40мм рк = 40 — 25 = 15мм ответ : рк = 15мм 3)кд = ке = 7см де = дк + ке, де = 7 + 7 = 14см значит fe = 2 * 14 = 28см ответ : 28 см.

Ну может бить там не 32 а 36 тогда растаяние будит равно 24 36 : 3 = 12 12 * 2 = 24.

32 — 12 = 20 это 1 часть а потом пишешь типо 20 : 2 10 и пому чаетмя.

Один угол равен Х, второй 2Х и третий Х — 20°. Сумма углов треугольника Х + 2Х + Х — 20° = 180°. 4Х = 200°, Х = 50°. Ответ .

1) N лежит между М и К : MK = MN + NK = 7 + 5 = 12 (см) 2) К лежит между M и N : MK = MN — KN = 7 — 5 = 2 ( см) Ответ : 12см, 2см.

1)угол в = 60 а угол с = 90. Так как он является прямым следовательно вс = 60 + 90 = 150.

АL — биссиктриса , значит делит угол BAC по полам следовательно угол ВАС = ВАL + LAC = 26 + 26 = 52°. Сумма углов треугольника равна 180° следовательно угол ABC = 180 — BAC — CAL = 180 — 52 — 61 = 67° угол АВС = 67°.

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/vpishite-v-okruzhnost-pravilnyy-dvenadtsatiugolnik

[/spoiler]

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 марта 2022 года; проверки требуют 3 правки.

Правильный двенадцатиугольник
Углы	12
Символ Шлефли	{12} t{6}

Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, двенадцатиугольником называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае двенадцатиугольника углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.

Правильный двенадцатиугольник[править | править код]

Площадь правильного двенадцатиугольника со стороной a находится по формуле:

Или, при радиусе описанной окружности R:

Или, при радиусе вписанной окружности r:

Монеты[править | править код]

Схема построения правильного двенадцатиугольника с помощью циркуля и линейки[править | править код]

Правильный двенадцатиугольник, согласно теореме Гаусса — Ванцеля, относится к многоугольникам, которые можно построить с помощью циркуля и линейки.

Разбиение правильного двенадцатиугольника[править | править код]

Гарольдом Коксетером было доказано, что правильный -угольник (в общем случае – -угольный зоногон) можно разбить на ромбов. Для двенадцатиугольника , так что он может быть разбит на 15 ромбов.

Разбиение правильного двенадцатиугольника

См. также[править | править код]

• Последовательность двенадцатиугольника

Ссылки[править | править код]

• Двенадцатиугольник Архивная копия от 28 июля 2011 на Wayback Machine на MathWorld
• Dodecagon (12-gon) Архивная копия от 25 ноября 2010 на Wayback Machine

Как найти сторону правильного многоугольника

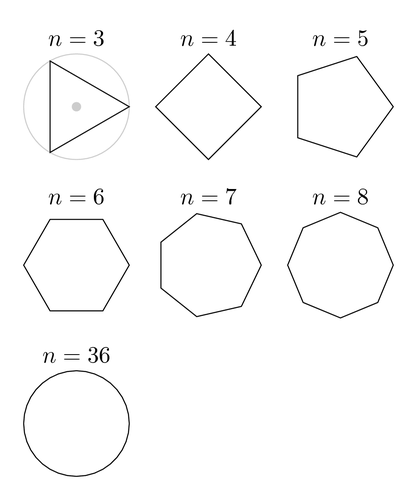
Фигура, образованная более чем из двух линий, замыкающихся между собой, называется многоугольником. Каждый многоугольник имеет вершины и стороны. Любой из них может быть правильным или неправильным.

Инструкция

Правильным многоугольником называется фигура, у которой все стороны равны. Так, например, равносторонний треугольник представляет собой правильный многоугольник, состоящий из трех замкнутых линий. В данном случае, все его углы равны 60 °. Его стороны между собой равны, но не параллельны друг другу. Таким же свойством обладают и другие многоугольники, однако, углы у них имеют другие величины. Единственный из правильных многоугольников, у которого стороны не только равны, но и попарно параллельны – квадрат.Если в задаче дан равносторонний треугольник с площадью S, то его неизвестную сторону можно найти через углы и стороны. Прежде всего, найдите высоту треугольника h, перпендикулярную к его основанию:h=a*sinα=a√3/2, где α=60° – один из углов, прилежащих к основанию треугольника.Руководствуясь этими соображениями, преобразуйте формулу для нахождения площади таким образом, чтобы по ней можно было вычислить длину стороны:S=1/2a*a√3/2=a^2*√3/4Отсюда следует, что сторона a равна:a=2√S/√√3

Сторону правильного четырехугольника найдите, пользуясь несколько иным способом. Если он представляет собой квадрат, в качестве первоначальных данных используйте его площадь или диагональ:S=a^2Следовательно, сторона a равна:a=√SКроме того, если дана диагональ, то сторону можно вычислить и по другой формуле:a=d/√2

В большинстве случаев сторону правильного многоугольника можно определить, зная радиус вписанной в него или описанной вокруг него окружности. Известно, что имеется взаимосвязь между стороной треугольника и радиусом окружности, описанной вокруг этой фигуры:a3=R√3, где R – радиус описанной окружностиЕсли окружность вписана в треугольник, то формула приобретает другой вид:a3=2r√3, где r – радиус вписанной окружностиУ правильного шестиугольника формула для нахождения стороны при известном радиусе описанной (R) или вписанной (r) окружностей выглядит следующим образом:a6=R=2r√3/3Из этих примеров можно сделать вывод, что для всякого произвольного n-угольника формула для нахождения стороны в общем виде выглядит следующим образом:a=2Rsin(α/2)=2rtg(α/2)

Источники:

• сторона правильного многоугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Задания

Версия для печати и копирования в MS Word