Задания
Версия для печати и копирования в MS Word
Тип 1 № 27916
i
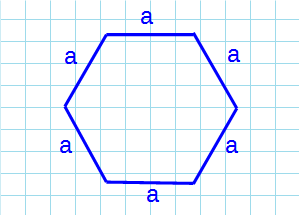
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Спрятать решение
Решение.
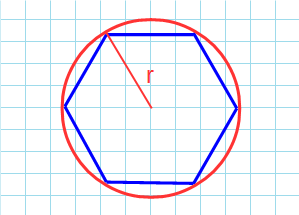
Пусть точка О — центр окружности. Треугольник АОВ является равнобедренным с углом при вершине 60° (см. рис.), поэтому этот треугольник равносторонний. Радиус ОН вписанной в шестиугольник окружности является высотой, биссектрисой и медианой треугольника АОВ, поэтому:
Ответ: 2.
Аналоги к заданию № 27916: 53571 53613 53619 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.7 Вписанная окружность и описанная окружность правильного многоугольника
Спрятать решение
·
Видеокурс
·
Помощь
Шестиугольник описанный около окружности формулы
На чтение 2 мин Просмотров 1.2к. Опубликовано 13.11.2021
Калькулятор для вычисления стороны правильного шестиугольника по известным данным.
При известном радиусе R описанной вокруг правильного шестиугольника окружности сторона a имеет такое же значение как и радиус R описанной вокруг шестиугольника окружности.
При известном радиусе r окружности вписанной в правильный шестиугольник сторона a вычисляется как отношение двух радиусов вписанной в правильный шестиугольник окружности и корня из числа 3.
Формула для вычисления стороны правильного шестиугольника при известном радиусе вписанной в правильный шестиугольник окружности:
r – радиус окружности вписанной в правильный шестиугольник,
a – сторона правильного шестиугольника.
При вводе данных дробную часть от целой, отделяйте точкой, а не запятой.
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник – многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
Формула для нахождения площади правильного шестиугольника через сторону:
Через радиус описанной окружности
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Как найти сторону многоугольника описанного около окружности
Ключевые слова: многоугольник, правильный многоугольник, сторона, угол, вписанная, описанная окружность
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
См. также:
Вписанная окружность, Описанная окружность, Выпуклый четырёхугольник, Произвольный выпуклый многоугольник
Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Правильный многоугольник
Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
a 1 = a 2 = a 3 = … = a n-1 = a n ,
α 1 = α 2 = α 3 = … = α n-1 = α n
где a1 … an — длины сторон правильного многоугольника,
α 1 … α n — внутренние углы между стронами правильного многоугольника.
Основные свойства правильного многоугольника
- Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
- Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
- Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольникаO.
- Сумма всех углов n-угольника равна: 180° · n – 2
- Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n – 3 2
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .
Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a = 2 · r · tg 180° n (через градусы),
a = 2 · r · tg π n (через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a = 2 · R · sin 180° n (через градусы),
a = 2 · R · sin π n (через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r = a : 2 · tg 180° n (через градусы),
r = a : 2 · tg π n (через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R = a : 2 · sin 180° n (через градусы),
R = a : 2 · sin π n (через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
Формула площади n-угольника через радиус вписанной окружности
Формула площади n-угольника через радиус описанной окружности
Формула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
Формула площади правильного треугольника через длину стороны
Формула площади правильного треугольника через радиус вписанной окружности
Формула площади правильного треугольника через радиус описанной окружности
Углы между сторонами правильного треугольника
Правильный четырехугольник
Правильный четырехугольник — это квадрат.
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
Формула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
Углы между сторонами правильного четырехугольника
Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности
Углы между сторонами правильного шестиугольника
Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
[spoiler title=”источники:”]
http://urokmatematiki.ru/reference-information/formuly-po-geometrii/pravilny-mnogougolnik.php
[/spoiler]
Как найти сторону правильного шестиугольника
Шестиугольную – «гексагональную» – форму имеют, например, сечения гаек и карандашей, пчелиных сот и снежинок. Правильные геометрические фигуры такой формы имеют некую особенность, отличающую их от прочих плоских многоугольников. Заключается она в том, что радиус описанной около гексагона окружности равен длине его стороны – во многих случаях это значительно упрощает вычисление параметров многоугольника.

Инструкция
Если в условиях задачи дан радиус (R) описанной около правильного шестиугольника окружности, вычислять ничего не придется – эта величина тождественна длине стороны (t) гексагона: t = R. При известном диметре (D) просто поделите его пополам: t = D/2.
Периметр (Р) правильного шестиугольника позволяет вычислить длину стороны (t) простой операцией деления. В качестве делителя используйте число сторон, т.е. шестерку: t = Р/6.
Радиус (r) вписанной в такой многоугольник окружности связан с длиной его стороны (t) немного более сложным коэффициентом – удвойте радиус, а полученный результат разделите на квадратный корень из тройки: t = 2*r/√3. Эта же формула с использованием диаметра (d) вписанной окружности станет на одно математическое действие короче: t = d/√3. Например, при радиусе в 50 см длина стороны шестиугольника должна быть приблизительно равна 2*50/√3 ≈ 57,735 см.
Известная площадь (S) многоугольника с шестью вершинами тоже позволяет вычислить длину его стороны (t), но численный коэффициент, связывающий их, точно выражается через дробь из трех натуральных чисел. Две трети площади делите на квадратный корень из тройки, а из полученного значения извлекайте квадратный корень: t = √(2*S/(3*√3)). Например, если площадь фигуры составляет 400 см², длина ее стороны должна составлять примерно √(2*400/(3*√3)) ≈ √(800/5,196) ≈ √153,965 ≈ 12,408 см.
Длина окружности (L), описанной около правильного шестиугольника, связана с радиусом, а значит и с длиной стороны (t) через число Пи. Если он дана в условиях задачи, поделите ее величину на два числа Пи: t = L/(2*π). Скажем, если эта величина равна 400 см, длина стороны должна составлять приблизительно 400/(2*3,142) = 400/6,284 ≈ 63,654 см.
Этот же параметр (l) для вписанной окружности позволяет рассчитать длину стороны шестиугольника (t) вычислением соотношения между ней и произведением числа Пи на квадратный корень из тройки: t = l/(π*√3). Например, если длина вписанной окружности составляет 300 см, сторона шестиугольника должна иметь величину, примерно равную 300/(3,142*√3) ≈ 300/(3,142*1,732) ≈ 300/5,442 ≈ 55,127 см.
Видео по теме
Источники:
- сторона шестиугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.