Чему равна и как найти площадь равностороннего треугольника
Равносторонний треугольник — это самый простой правильный многоугольник из возможных. При нахождении его площади возникают частные варианты его расчета. Важно знать и понимать признаки и свойства этого вида фигур, для более легкого вычисления этого параметра. Все методы, представленные ниже, достаточно просты в применении, и не потребуют глубокого осмысления….
Признаки и свойства фигуры
Для того чтобы рассчитать его площадь необходимо понимать свойства и признаки, которыми он обладает. Можно выделить следующие основные признаки этой фигуры:
- Значение величины его углов одинаково во всех случаях и равняется 60 градусам, вне зависимости от размера сторон.
- Биссектриса, высота и медиана выпущенные из одного угла будут совпадать.
- Любая сторона равностороннего треугольника равна двум другим.
- Центр правильного треугольника будет являться центром для вписанной и описанной окружности.
- Является частным случаем равнобедренного треугольника.
Важно! Если хотя бы один из этих признаков соблюдается, значит, треугольник является равносторонним. 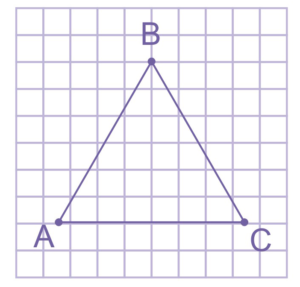
Дополнительно этот частный случай фигуры обладает следующими свойствами:
Расчет через сторону
Существует множество способов расчета площади этой фигуры. Все они имеют свои преимущества и недостатки. Применяются в зависимости от условий, представленных задаче. Самая популярный способ найти искомое значение для равностороннего треугольника вычисляется через произведение половины сторон и синуса угла между ними, выглядит это следующим образом: 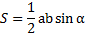
В случае с равносторонним, этот способ упрощается в значительной степени. Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все углы этой фигуры равны, и равняются 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется 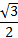
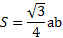
Учитывая то, что все стороны этой фигуры равны, то преобразованное выражение даст такой результат: 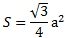
Данная формула отлично подойдет в случае, если известна величина стороны этой фигуры. В таком виде вычислять данный показатель гораздо легче и быстрее.
Те, кто помнит формула Герона, знают, как найти площадь этой фигуры. В процессе преобразования выражение изменится в представленное выше. Площадь этой фигуры по Герону рассчитывается так: 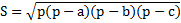
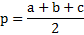
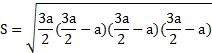
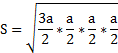
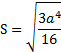
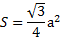
Полученная формула площади и представленные ниже функции могут быть использованы только, в случае, если фигура является правильной, в ином случае не будет давать правильный ответ.
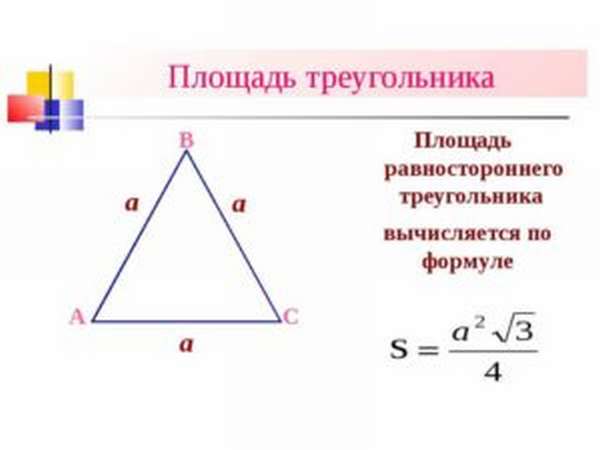
Расчет по высоте
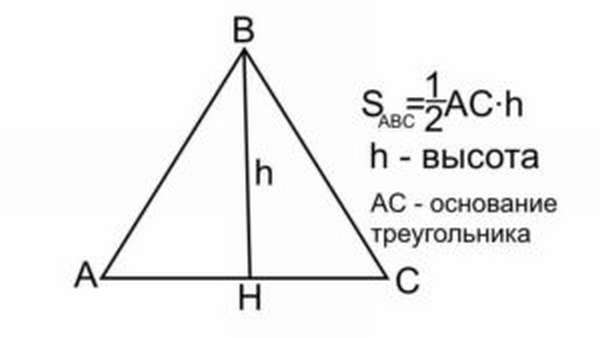
Найти площадь равностороннего треугольника можно также, если известна его высота и сторона. Половина длины высоты умножается на сторону, выбрана может быть любая высота и сторона, ведь согласно свойствам, они все одинаковые: 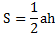
Если в задаче указана информация о том, что треугольник является равносторонним и известна величина высоты. А чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее рассчитать. Найти сторону можно разделив двойную величину высоты на корень квадратный из трех, математически выглядит следующим образом: 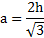
Для того чтобы не делать лишних расчетов можно вывести формулу этого показателя сразу же через высоту. Квадрат высоты делится на корень квадратный из трех. Она будет выглядеть так: 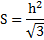
Расчет через окружности
В математике популярен также прием расчета, рассматриваемого в статье, значения через помещение фигуры в окружность или наоборот. Такая окружность называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.
Описанная окружность обязательно должна проходить через все вершины, вписанная должна проходить через стороны только в одной точке по касательной.
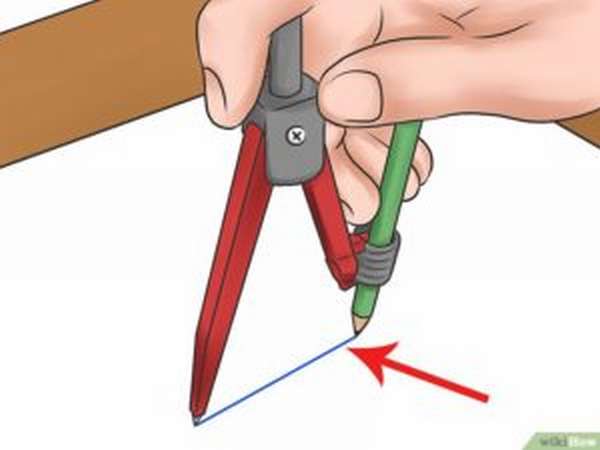
Если в условии задачи дан радиус вписанной и описанной окружности, то из них также можно составить выражение, так как вместе они дадут суммарную длину высоты. Как рассчитывается площадь при ее помощи, показано выше: h = R + r .
Преобразовав формулу 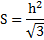
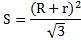
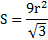
Если же будет дан размер радиуса описанной окружности, то выражение будет выглядеть следующим образом: 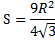
Использование этих свойств пригодится для расчета стороны фигуры. Для того чтобы ее найти можно воспользоваться выражением 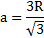
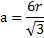
Учитывая радиус описанной окружности можно найти искомое значение при помощи возведения стороны в куб, после чего результат делится на радиус, увеличенный в 4 раза. Математически его можно записать следующим образом: 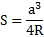
Процесс расчета, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.
Внимание! Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть.
Площадь равностороннего треугольника
Площадь равностороннего треугольника, вписанного в окружность
Применив логическое мышление, расчеты с легкостью преобразовываются в частные случаи, коих гораздо больше. Нецелесообразно забивать голову большим количеством нерелевантной информации, лучше развивать причинно-следственную связь для преобразования выражений.
Правильный треугольник. Площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/pravilnyj-treugolnik-i-ego-ploshhad/
http://colibrus.ru/treugolnik-vpisannyy-v-okruzhnost/
[/spoiler]
Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.
- Сторона треугольника равностороннего через радиус описанной
окружности - Сторона треугольника равностороннего через радиус вписанной
окружности - Сторона треугольника равностороннего через высоту
- Сторона треугольника равностороннего через площадь
треугольника - Основание равнобедренного треугольника через боковые
стороны и угол между ними - Основание равнобедренного треугольника через боковые
стороны и угол при основании - Боковая сторона равнобедренного треугольника через
основание и угол между боковыми сторонами - Боковая сторона равнобедренного треугольника через
основание и угол при основании - Катет прямоугольного треугольника через гипотенузу и острый
угол - Катет прямоугольного треугольника через гипотенузу и другой
известный катет - Гипотенуза прямоугольного треугольника через катет и острый
угол - Гипотенуза прямоугольного треугольника через катеты
- Сторона треугольника через две известные стороны и угол
между ними - Сторона треугольника через известную сторону и два угла
Сторона равностороннего треугольника через радиус описанной окружности
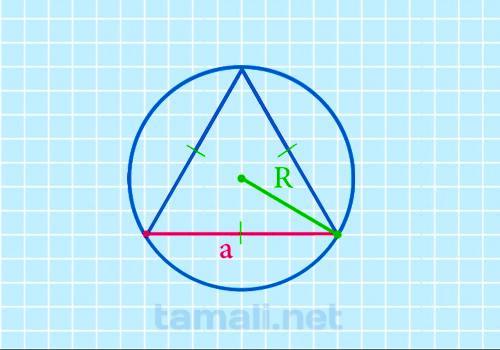
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:
a = R * √3
где а — сторона треугольника, R — радиус описанной окружности.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.
Сторона равностороннего треугольника через радиус вписанной окружности
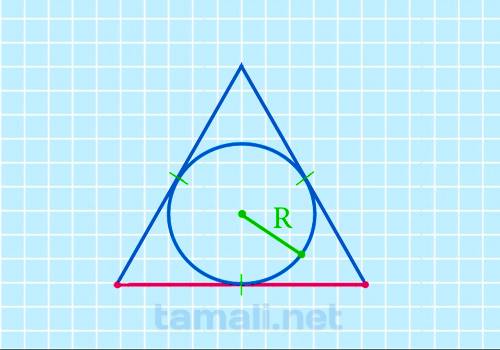
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):
a = 2r * √3
где а — сторона треугольника, R — радиус вписанной окружности.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.
Сторона равностороннего треугольника через высоту
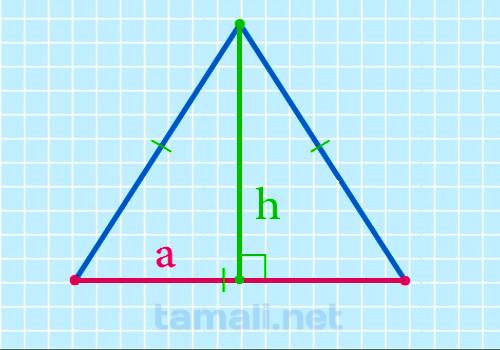
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:
a = 2h / √3
где а — сторона, h — высота равностороннего треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.
Сторона равностороннего треугольника через площадь
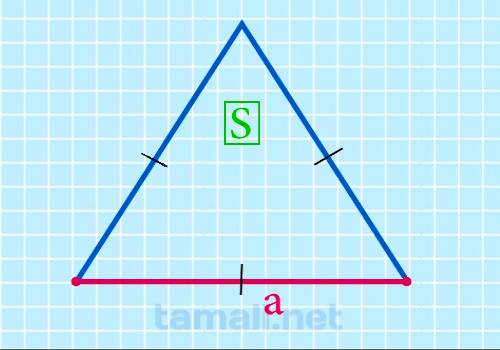
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу
a = √(4S / √3)
где а — сторона, S — площадь равностороннего треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.
Основание равнобедренного треугольника через боковые стороны и угол между ними
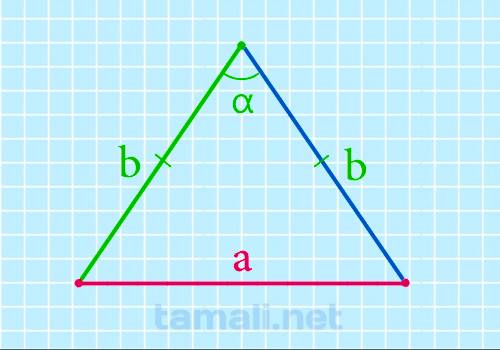
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:
a = 2b * sin (α/2)
где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.
Основание равнобедренного треугольника через боковые стороны и угол при основании
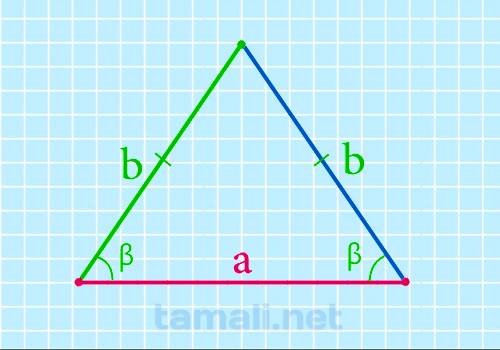
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:
a = 2b + cos β
где b — боковая сторона, β — угол при основании.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.
Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами
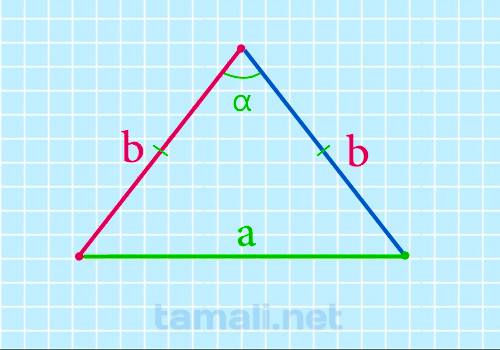
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным. Это значит, что α = β.
Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:
b = a / (2 * sin(α/2))
где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.
Боковая сторона равнобедренного треугольника через основание и угол при основании
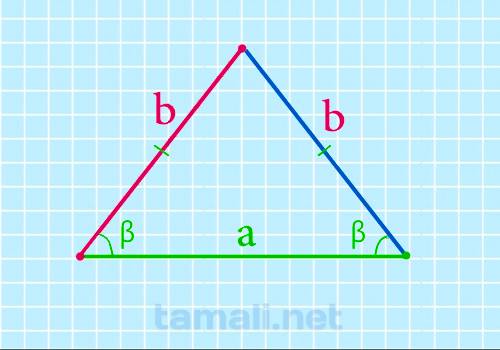
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:
b = a / 2 * cos β
где a — это основание, β — угол при основании равнобедренного треугольника.
Цифр после
запятой:
Результат в:
Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.
Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.
Катет прямоугольного треугольника через гипотенузу и острый угол
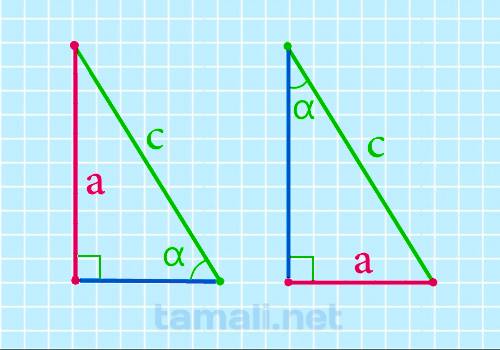
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:
a = c * sin α
где c — гипотенуза, α — острый угол прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее: a = 77 * 0,98 = 75,8см.
Катет прямоугольного треугольника через гипотенузу и другой известный катет
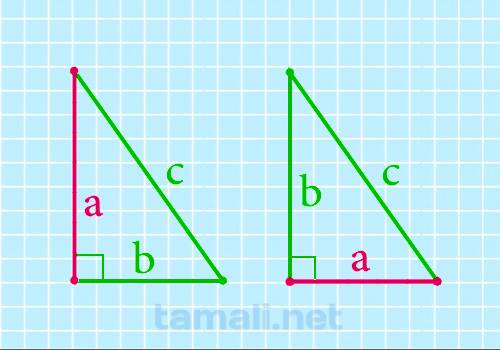
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:
a = √(c² — b²)
где c — гипотенуза, b — катет который известен прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см
Гипотенуза прямоугольного треугольника через катет и острый угол
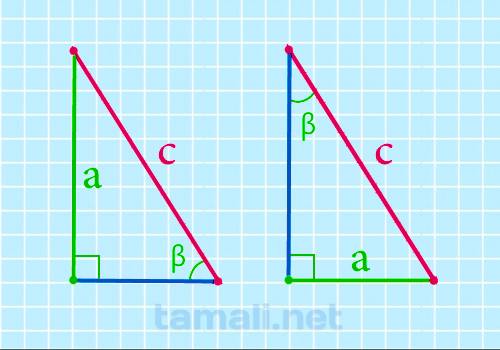
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:
c = a / sin(β)
где a — катет, β — острый угол прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.
Гипотенуза прямоугольного треугольника через катеты
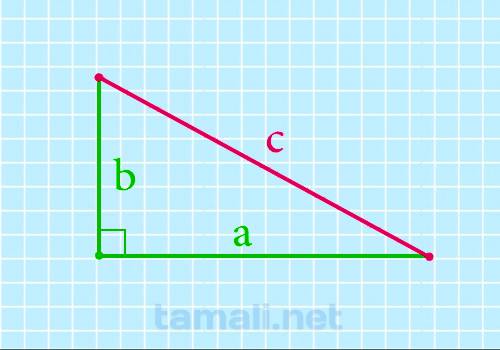
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:
c = √(a² + b²)
где c — гипотенуза, a и b — катеты.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см
Сторона треугольника через две известные стороны и угол между ними
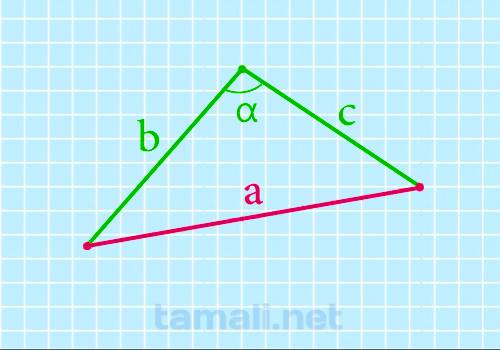
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:
a = b² + c² — 2bc * cos α
где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.
Цифр после
запятой:
Результат в:
Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.
Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.
Сторона треугольника через известную сторону и два угла
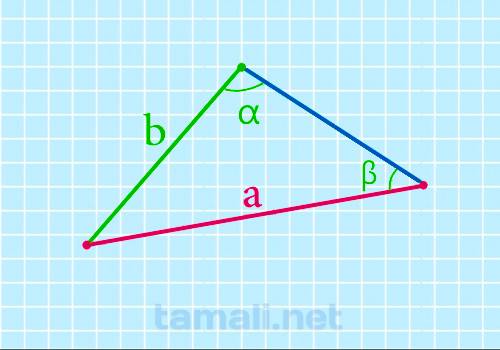
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:
a = (b * sin α) / sin β
где b — сторона треугольника; β, α — углы треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть сторона треугольника b равна 10, угол β = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30 = 8.71723 мм.
Как найти сторону правильного треугольника
«Правильным» называют треугольник, все стороны которого равны между собой, равно как и углы в его вершинах. В евклидовой геометрии углы в вершинах такого треугольника не нуждаются в вычислениях – они всегда равны 60°, а длину сторон можно вычислить по относительно несложным формулам.
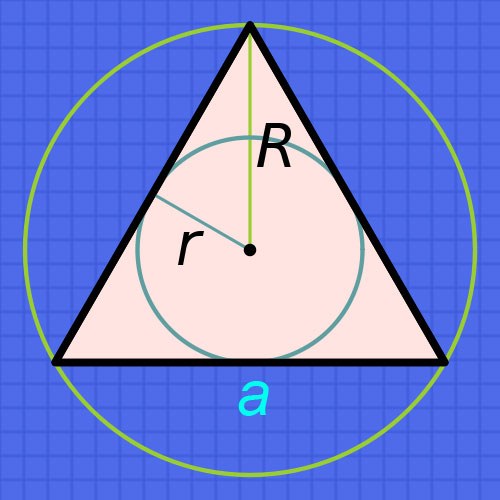
Инструкция
Если известен радиус окружности (r), вписанной в правильный треугольник, то для нахождения длин его сторон (a), увеличьте радиус в шесть раз и разделите результат на квадратный корень из тройки: a=r•6/√3. Например, если этот радиус равен 15 сантиметрам, то длина каждой стороны приблизительно будет равна 15•6/√3≈90/1,73≈52,02 сантиметрам.
Если известен радиус не вписанной, а описанной возле такого треугольника окружности (R), то исходите из того, что радиус описанной окружности всегда вдвое больше радиуса вписанной. Из этого вытекает, что формула расчета длины стороны (a) будет почти совпадать с описанной на предыдущем шаге – увеличьте известный радиус только в три раза, а результат разделите на квадратный корень из тройки: a=R•3/√3. Например, если радиус такой окружности равен 15 сантиметрам, то длина каждой стороны приблизительно будет равна 15•3/√3≈45/1,73≈26,01 сантиметрам.
Если известна высота (h), проведенная из любой вершины правильного треугольника, то для нахождения длины каждой его стороны (a) находите частное от деления удвоенной высоты на квадратный корень из тройки: a=h•2/√3. Например, если высота составляет 15 сантиметров, то длины сторон будут равны 15•2/√3≈60/1,73≈34,68 сантиметра.
Если известна длина периметра правильного треугольника (P), то для нахождения длин сторон (a) этой геометрической фигуры просто уменьшите его втрое: a=P/3. Например, если периметр составляет 150 сантиметров, то длина каждой из сторон будет равна 150/3=50 сантиметрам.
Если известна только площадь такого треугольника (S), то для нахождения длины каждой его стороны (a) посчитайте квадратный корень из частного от деления учетверенной площади на квадратный корень из тройки: a=√(4•S/√3). Например, если площадь равна 150 квадратным сантиметрам, то длина каждой стороны приблизительно будет равна √(4•150/√3)≈√(600/1,73)≈18,62 сантиметрам.
Источники:
- сторона правильного треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Содержание
- 1 Свойства
- 2 Правильный сферический треугольник
- 3 Теоремы о равностороннем треугольнике или содержащие его
- 4 См. также
- 5 Примечания
Свойства[править | править код]
Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
- Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- Периметр правильного треугольника:
- Высоты, медианы и биссектрисы правильного треугольника:
- Площадь правильного треугольника рассчитывается по формулам:
- Радиус описанной окружности равен двойному радиусу вписанной окружности:
- Правильными треугольниками можно замостить плоскость.
- В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
Правильный сферический треугольник[править | править код]
Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.
Теоремы о равностороннем треугольнике или содержащие его[править | править код]
- Задача Наполеона
- Прямая Симсона одно из свойств
- Теорема Вивиани
- Теорема Морли
- Теорема Наполеона
- Теорема Помпею
- Теоремы Тебо 2 и 3
- Точки Аполлония
- Точки Торричелли
См. также[править | править код]
- Замечательные прямые треугольника
- Замечательные точки треугольника
- Равнобедренный треугольник
- Теорема Чевы
- Треугольник
- Треугольник Рёло
Примечания[править | править код]
Символ Шлефли |
|
|---|---|
| Многоугольники |
|
| Звёздчатые многоугольники |
|
| Паркеты на плоскости |
|
| Правильные многогранники и сферические паркеты |
|
| Многогранники Кеплера — Пуансо |
|
| Соты |
{4,3,4} |
| Четырёхмерные многогранники |
|
Содержание
- Определение правильного многоугольника
- Элементы правильного многоугольника
- Диагонали n — угольника
- Внешний угол многоугольника
- Сумма внутренних углов
- Сумма внешних углов
- Виды правильных многоугольников
- Основные свойства правильного многоугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Доказательства свойств углов многоугольника
- Правильный n-угольник — формулы
- Формулы длины стороны правильного n-угольника
- Формула радиуса вписанной окружности правильного n-угольника
- Формула радиуса описанной окружности правильного n-угольника
- Формулы площади правильного n-угольника
- Формула периметра правильного многоугольника:
- Формула определения угла между сторонами правильного многоугольника:
- Формулы правильного треугольника:
- Формулы правильного четырехугольника:
- Формулы правильного шестиугольника:
- Формулы правильного восьмиугольника:
- Сторона правильного многоугольника через радиус описанной вокруг него окружности
- Шаг 1
- Шаг 2
- Шаг 3
Определение правильного многоугольника
Правильный многоугольник – это выпуклый многоугольник, у которого равны все стороны и углы.
Признаки правильного n-угольника
- a1 = a2 = a3 = … an-1 = an
- α1 = α2 = α3 = … αn-1 = αn
Примечание: n – количество сторон/углов фигуры.
Элементы правильного многоугольника
Для рисунка выше:
- a – сторона/ребро;
- α – угол между смежными сторонами;
- O – центр фигуры/масс (совпадает с центрами описанной и вписанной окружностей);
- β – центральный угол описанной окружности, опирающийся на сторону многоугольника.
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника |
 |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
 |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
 |
Число диагоналейn – угольника равно |
| Диагональ многоугольника |

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |

Число диагоналей n – угольника равно |
Внешний угол многоугольника
Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Рис.2
Замечание. Мы рассматриваем только выпуклые многоугольники выпуклые многоугольники .
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
s = 2d(n — 2),
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
s = 2d(n — 2) = 180 · 4 = 720°.
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
s = 4d,
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.
Виды правильных многоугольников
- Правильный (равносторонний) треугольник
- Правильный четырехугольник (квадрат)
- Правильный пяти-, шести-, n-угольник
Основные свойства правильного многоугольника
- Все стороны равны:
a1 = a2 = a3 = … = an-1 = an2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O4. Сумма всех углов n-угольника равна:
180° · (n — 2)
- Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
- В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Свойство 1
Внутренние углы в правильном многоугольнике (α) равны между собой и могут быть рассчитаны по формуле:
где n – число сторон фигуры.
Свойство 2
Сумма всех углов правильного n-угольника равняется: 180° · (n-2).
Свойство 3
Количество диагоналей (Dn) правильного n-угольника зависит от количества его сторон (n) и определяется следующим образом:
Свойство 4
В любой правильный многоугольник можно вписать круг и описать окружность около него, причем их центры будут совпадать, в том числе, с центром самого многоугольника.
В качестве примера на рисунке ниже изображен правильный шестиугольник (гексагон) с центром в точке O.
Площадь (S) образованного окружностями кольца вычисляется через длину стороны (a) фигуры по формуле:
Между радиусами вписанной (r) и описанной (R) окружностей существует зависимость:
Свойство 5
Зная длину стороны (a) правильного многоугольника можно рассчитать следующие, относящиеся к нему величины:
- Площадь (S):
- Периметр (P):
- Радиус описанной окружности (R):
- Радиус вписанной окружности (r):
Свойство 6
Площадь (S) правильного многоугольника можно выразить через радиус описанной/вписанной окружности:
Доказательства свойств углов многоугольника
Теорема 1. В любом треугольнике сумма углов равна 180°.
Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Рис.3
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Замечание. Теорема 1 является следствием теоремы 2.
Теорема 3. Сумма углов – угольникаn равна
Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Рис.5
Получим n треугольников:
OA1A2, OA2A3, … OAnA1
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4. Сумма внешних углов – угольникаn , взятых по одному у каждой вершины, равна 360°.
Доказательство. Рассмотрим рисунок 6.
Рис.6
В соответствии рисунком 6 справедливы равенства
Теорема доказана.
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
- Формула стороны правильного n-угольника через радиус вписанной окружности:
- Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
- Формула площади n-угольника через длину стороны:
- Формула площади n-угольника через радиус вписанной окружности:
- Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
 |
| Рис.3 |
Формулы правильного треугольника:
- Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
- Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
- Формула радиуса вписанной окружности правильного треугольника через длину стороны:
- Формула радиуса описанной окружности правильного треугольника через длину стороны:
- Формула площади правильного треугольника через длину стороны:
- Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
- Формула площади правильного треугольника через радиус описанной окружности:
- Угол между сторонами правильного треугольника:
α = 60°
 |
| Рис.4 |
Формулы правильного четырехугольника:
- Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
- Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
- Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
- Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
- Формула площади правильного четырехугольника через длину стороны:
S = a2
- Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
- Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
- Угол между сторонами правильного четырехугольника:
α = 90°
Формулы правильного шестиугольника:
Формула стороны правильного шестиугольника через радиус вписанной окружности:
Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
Формула площади правильного шестиугольника через длину стороны:
Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Формулы правильного восьмиугольника:
Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
Угол между сторонами правильного восьмиугольника:
α = 135°
Сторона правильного многоугольника через радиус описанной вокруг него окружности
Сторону правильного многоугольника через радиус описанной вокруг него окружности можно найти по формуле
Где:
a – длина его стороны;
R – радиус описанной окружности;
n – число сторон многоугольника.
Формула стороны правильного многоугольника
Шаг 1
Рассмотрим правильный многоугольник А1А2А3…Аn.
Пусть его сторона будет равна a.
Опишем вокруг этого многоугольника окружность с центром в точке О и радиусом R.
Вывод формулы стороны правильного многоугольника.
Шаг 2
Соединим точку О с его вершинами. А1А2А3…Аn.
Рассмотрим треугольник ОА1А2.
Рассматриваемый треугольник будет равнобедренным, так как его стороны А1О и А2О – радиусы описанной окружности.
Проведем в треугольнике А1ОА2 высоту ОК.
Так как треугольник А1ОА2 равнобедренный, то высота будет медианой:
Вывод формулы стороны правильного многоугольника.
Шаг 3
Рассмотрим треугольник А1КО.
Этот треугольник прямоугольный, так как ОК – высота по построению.
Так как точка О – центр правильного многоугольника, то отрезки АnO являются биссектрисами углов этого многоугольника.
Таким образом, если углы многоугольника обозначим буквой α, то угол ОА1К будет равен:
По свойству углов правильного многоугольника, каждый угол равен:
Тогда угол ОА1К будет равен:
Из определения косинуса угла получим:
Отсюда:
Подставим в формулу значения, полученные выше и на шаге 2:
Умножим обе части уравнения на 2:
Воспользуемся формулами приведения
Так как А1О является радиусом описанной окружности, то сторона правильного многоугольника может быть найдена по формуле:
Вывод формулы стороны правильного многоугольника.



























