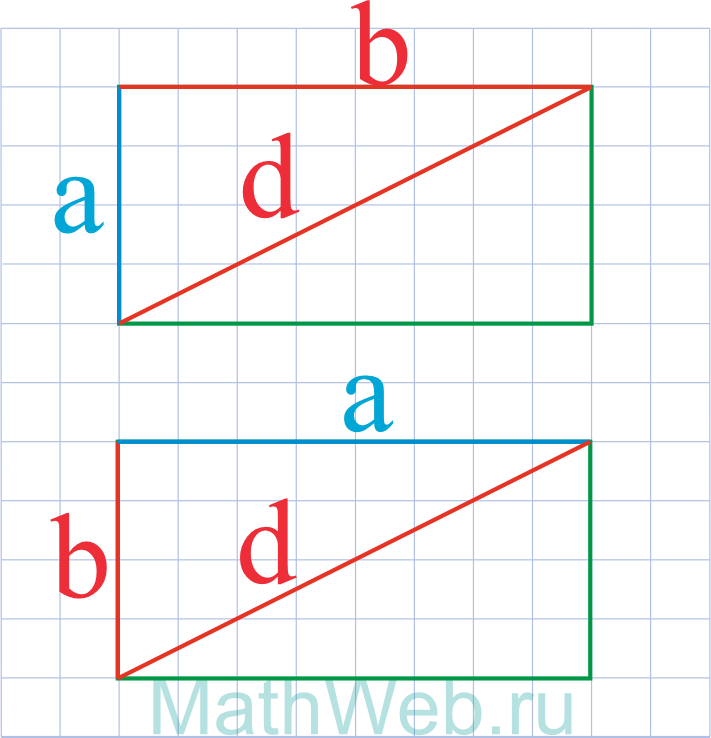
Где d – диагональ,b – сторона.
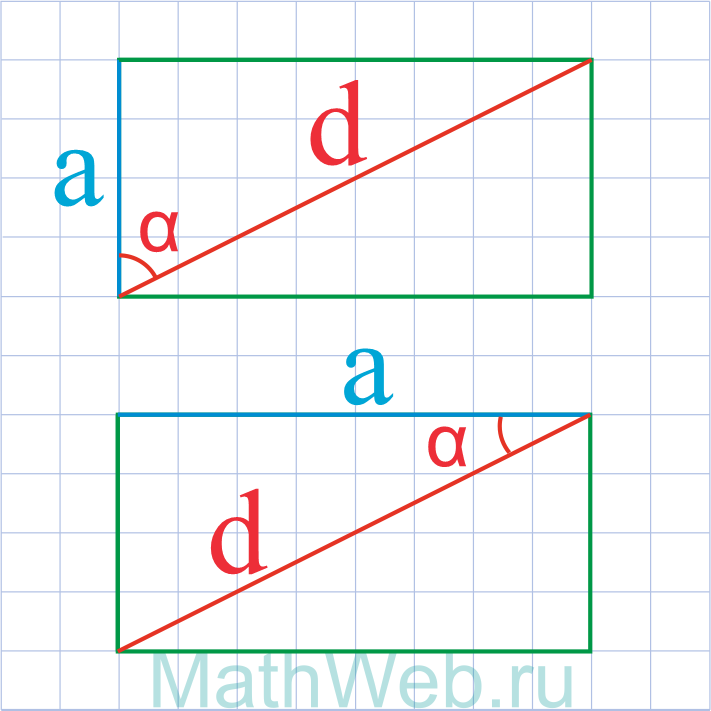
Где d – диагональ,α – угол между диагональю и искомой стороной.
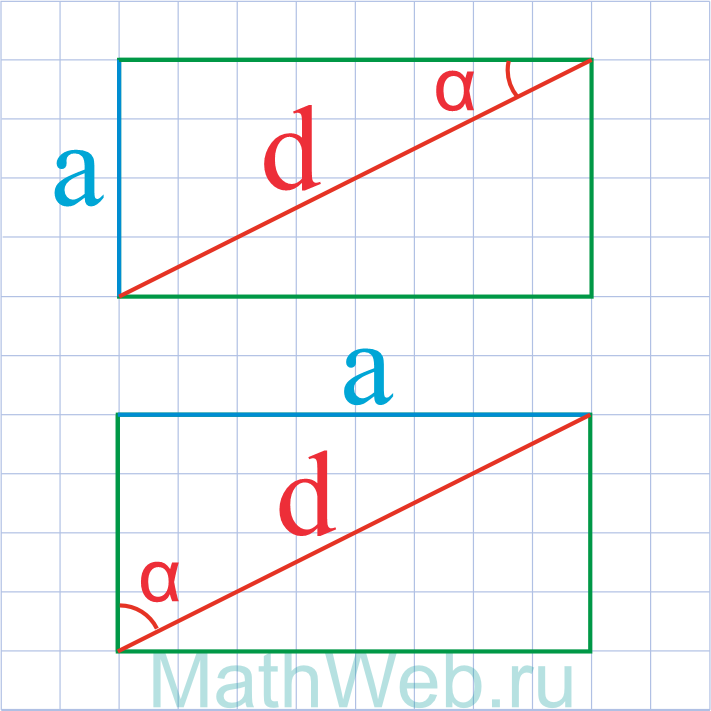
Где d – диагональ,α – угол между диагональю и другой стороной.
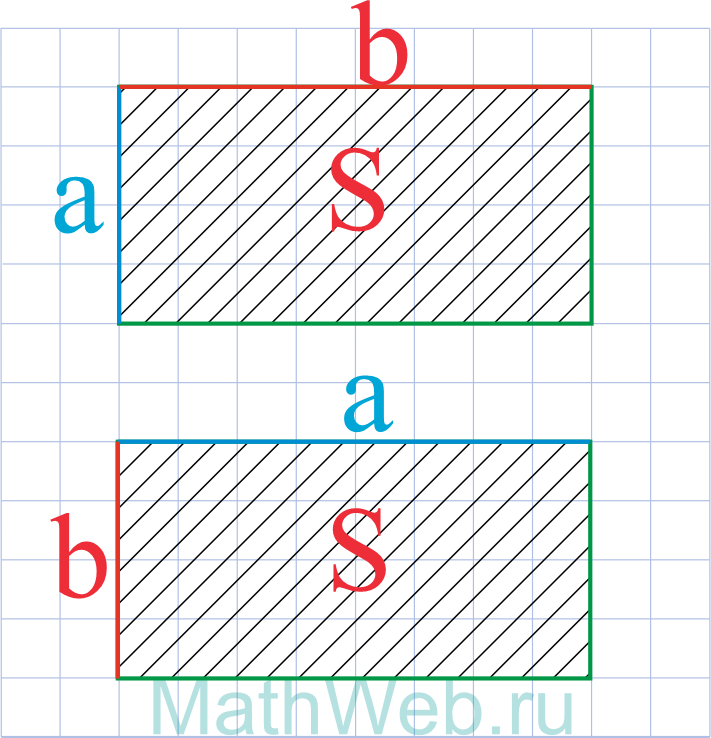
Где S – площадь, b– известная сторона.
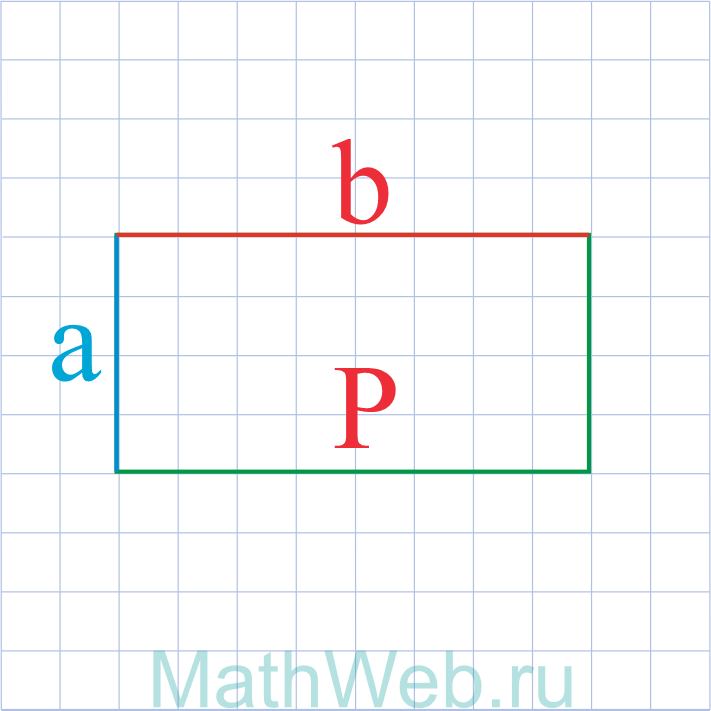
Где P – периметр, b – известная сторона.
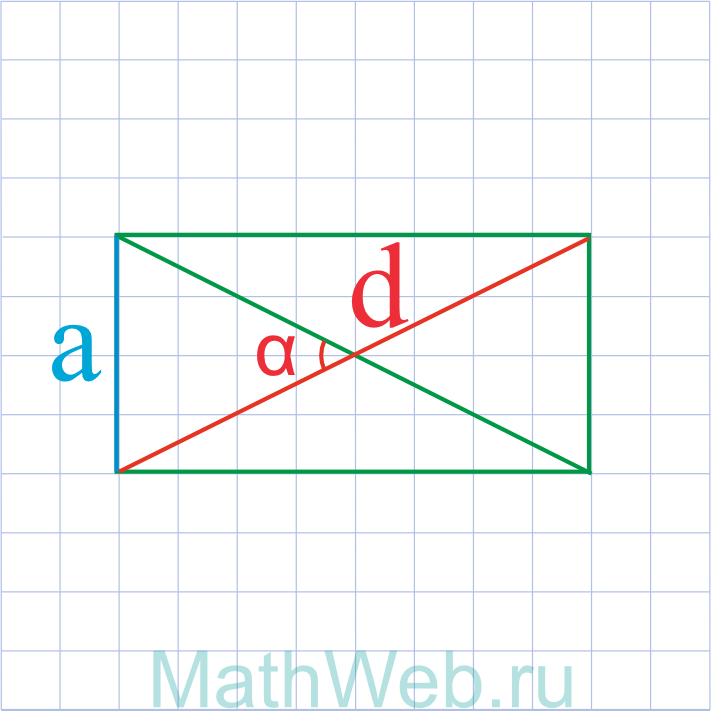
Где d – диагональ, α – угол между диагоналями.
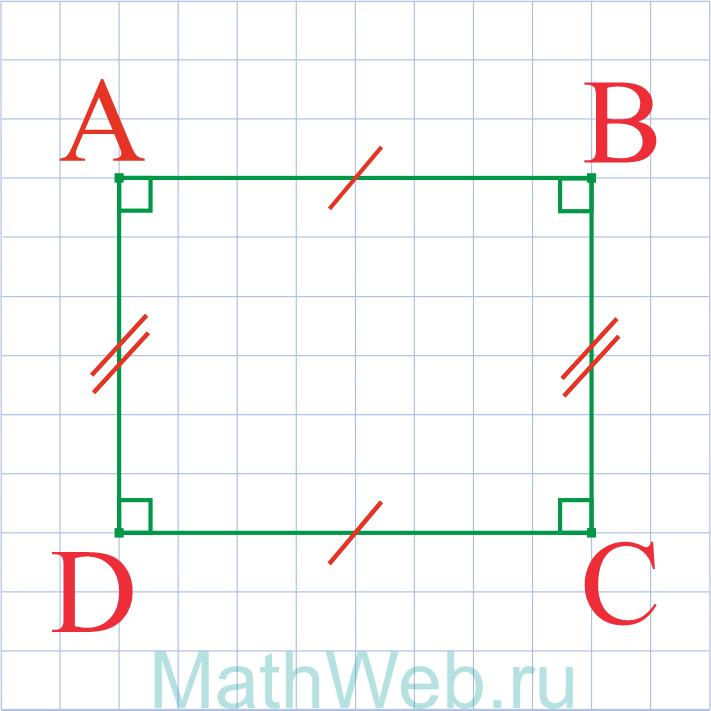
- Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = √d2 ― b2 |
 |
a = d·cos(α) |
 |
a = d·sin(α) |
 |
a = S b |
 |
a = P – 2b 2 |
 |
a = d·sin(0.5·α) |
Содержание:
Теорема синусов, теорема косинусов:
Теорема синусов
Вы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть 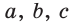
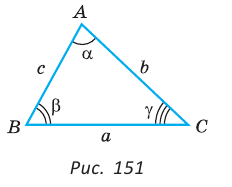
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
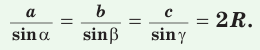
Доказательство:
Пусть дан треугольник АВС, ВС = 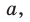
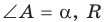 — радиус его описанной окружности. Угол а может быть острым, тупым или прямым. Рассмотрим эти случаи отдельно.
— радиус его описанной окружности. Угол а может быть острым, тупым или прямым. Рассмотрим эти случаи отдельно.
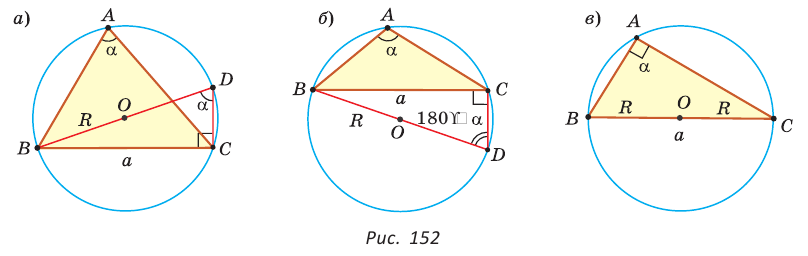
1) Угол 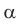 острый (рис. 152, а). Проведя диаметр BD и отрезок DC, получим прямоугольный треугольник BCD, в котором
острый (рис. 152, а). Проведя диаметр BD и отрезок DC, получим прямоугольный треугольник BCD, в котором 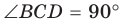 как вписанный угол, опирающийся на диаметр. Заметим, что
как вписанный угол, опирающийся на диаметр. Заметим, что 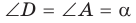 как вписанные углы, опирающиеся на одну и ту же дугу ВС. Из прямоугольного треугольника BCD находим
как вписанные углы, опирающиеся на одну и ту же дугу ВС. Из прямоугольного треугольника BCD находим 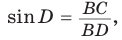 т. е.
т. е. 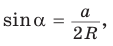 откуда
откуда 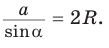
2) Угол 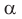 тупой (рис. 152, б). Проведем диаметр BD и отрезок DC. В четырехугольнике ABDC по свойству вписанного четырехугольника
тупой (рис. 152, б). Проведем диаметр BD и отрезок DC. В четырехугольнике ABDC по свойству вписанного четырехугольника 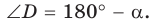 Из прямоугольного треугольника
Из прямоугольного треугольника 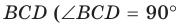 как вписанный угол, опирающийся на диаметр)
как вписанный угол, опирающийся на диаметр) 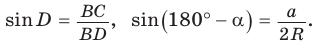 Поскольку
Поскольку 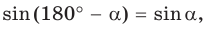 то
то 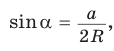 откуда
откуда 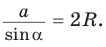
3) Для 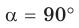 справедливость равенства
справедливость равенства 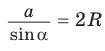 докажите самостоятельно, В силу доказанного
докажите самостоятельно, В силу доказанного 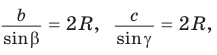 откуда
откуда 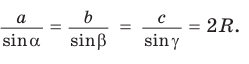
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция 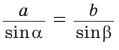 позволяет решить две следующие задачи:
позволяет решить две следующие задачи:
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы 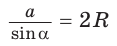 можно решить еще три задачи (рис. 153):
можно решить еще три задачи (рис. 153):
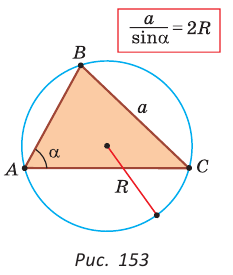
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
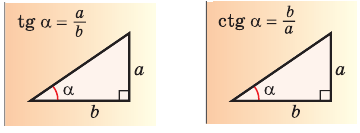
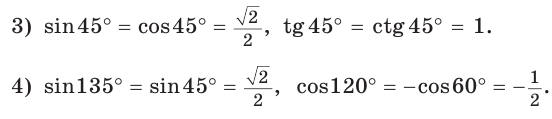
Пример:
В остроугольном треугольнике известны стороны 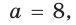
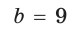 и угол
и угол 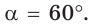 Найти два других угла
Найти два других угла 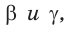 округлив их значения до 1°, и третью сторону треугольника, округлив ее длину до 0,1.
округлив их значения до 1°, и третью сторону треугольника, округлив ее длину до 0,1.
Решение:
По теореме синусов 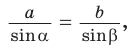 откуда
откуда 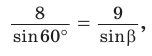
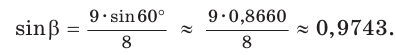 При помощи калькулятора (таблиц). находим
При помощи калькулятора (таблиц). находим 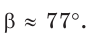 Тогда
Тогда 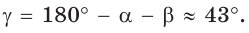 По теореме синусов
По теореме синусов 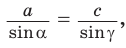 откуда
откуда 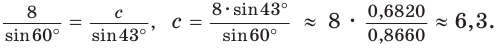
Ответ: 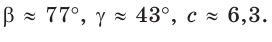
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом 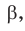 то, зная
то, зная 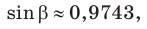 вначале мы нашли бы острый угол
вначале мы нашли бы острый угол 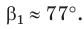 А затем, используя формулу
А затем, используя формулу 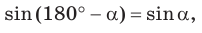 получили бы, что
получили бы, что 

Пример:
Доказать справедливость формулы площади треугольника 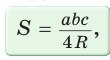 где
где 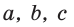 — его стороны, R — радиус описанной окружности.
— его стороны, R — радиус описанной окружности.
Доказательство:
Воспользуемся известной формулой площади треугольника: 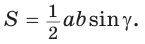 По теореме синусов
По теореме синусов 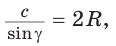 откуда
откуда 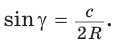 Тогда
Тогда 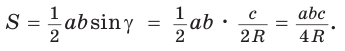 Что и требовалось доказать.
Что и требовалось доказать.
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника 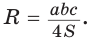
Пример:
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
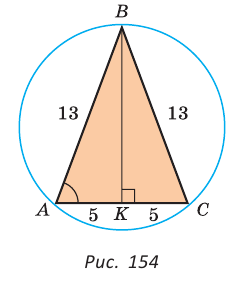
Решение:
Способ 1. Из формулы 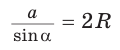 следует, что
следует, что 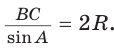 Найдем
Найдем 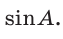 . Для этого в треугольнике АВС проведем высоту ВК, которая будет и медианой, откуда
. Для этого в треугольнике АВС проведем высоту ВК, которая будет и медианой, откуда 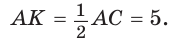 Из
Из 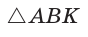 по теореме Пифагора
по теореме Пифагора 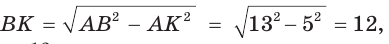 откуда
откуда 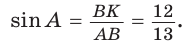
Тогда 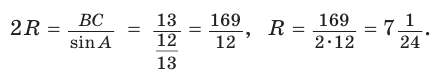
Способ 2. Используем формулу 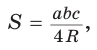 из которой
из которой 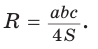 Так как
Так как 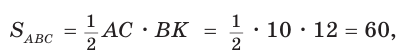 то
то 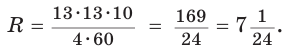
Ответ: 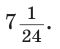
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу 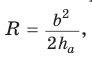 где
где 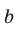 — боковая сторона,
— боковая сторона, 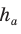 — высота, проведенная к основанию
— высота, проведенная к основанию 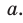
Заменив 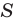 в формуле
в формуле 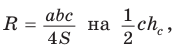 получим
получим 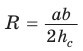 — формулу радиуса описанной окружности для произвольного треугольника. Итак, мы имеем четыре формулы для нахождения радиуса R описанной окружности треугольника:
— формулу радиуса описанной окружности для произвольного треугольника. Итак, мы имеем четыре формулы для нахождения радиуса R описанной окружности треугольника:

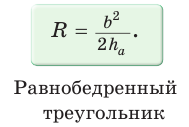
Теорема косинусов
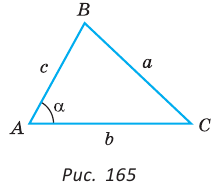
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 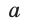 треугольника АВС (рис. 165) через длины сторон
треугольника АВС (рис. 165) через длины сторон 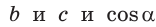 ). Теорему косинусов можно назвать самой «работающей» в геометрии. Она имеет многочисленные следствия, которые часто используются при решении задач.
). Теорему косинусов можно назвать самой «работающей» в геометрии. Она имеет многочисленные следствия, которые часто используются при решении задач.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
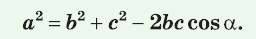
Доказательство:
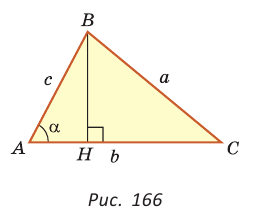
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из 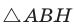 находим
находим 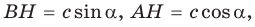 откуда
откуда 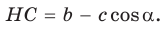
Из 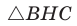 по теореме Пифагора
по теореме Пифагора 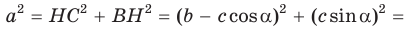
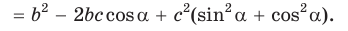
По основному тригонометрическому тождеству 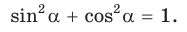
Тогда 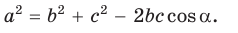
Справедливость теоремы для случаев, когда 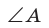 или
или 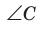 тупой или прямой, докажите самостоятельно. Теорема доказана.
тупой или прямой, докажите самостоятельно. Теорема доказана.
Для сторон 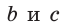 теорема косинусов запишется так:
теорема косинусов запишется так:
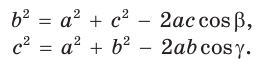
Замечание. Если 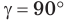 , то по теореме Пифагора
, то по теореме Пифагора 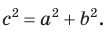 Так как
Так как 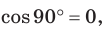 то
то 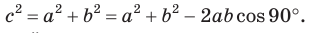 Таким образом, теорема Пифагора — частный случай теоремы косинусов.
Таким образом, теорема Пифагора — частный случай теоремы косинусов.
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
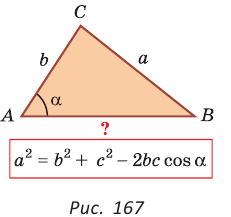
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 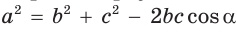 следует формула
следует формула
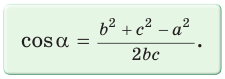
Для углов 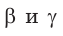 получим:
получим:
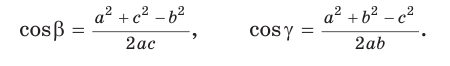
Пример:
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
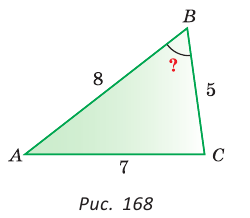
По теореме косинусов

Используя записанную выше формулу, можно сразу получить:
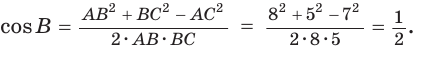
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 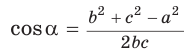 с учетом того, что
с учетом того, что 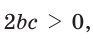 следует:
следует:
- если
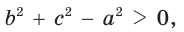 то
то 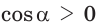 и угол
и угол 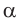 острый;
острый; - если
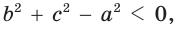 то
то 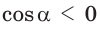 и угол
и угол 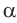 тупой;
тупой; - если
 то
то 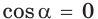 и угол
и угол 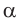 прямой.
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 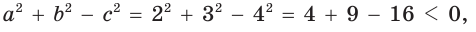 то
то 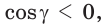 угол
угол 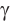 тупой и данный треугольник тупоугольный.
тупой и данный треугольник тупоугольный.
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
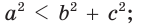
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
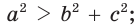
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
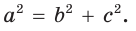
Следствие:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: 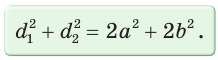
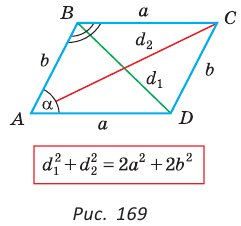
Доказательство:
Пусть в параллелограмме ABCD 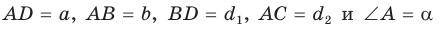 — острый, откуда
— острый, откуда 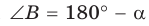 — тупой (рис. 169). По теореме косинусов из
— тупой (рис. 169). По теореме косинусов из 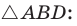
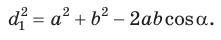 (1)
(1)
Из 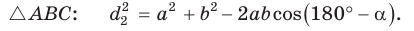 Поскольку cos
Поскольку cos 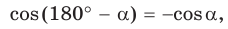 то
то
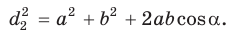 (2)
(2)
Сложив почленно равенство (1) и равенство (2), получим 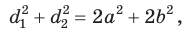 что и требовалось доказать.
что и требовалось доказать.
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
Медиану 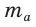 треугольника со сторонами а, b и с можно найти по формуле
треугольника со сторонами а, b и с можно найти по формуле 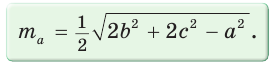
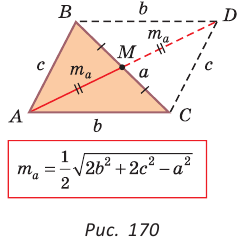
Доказательство:
Рассмотрим 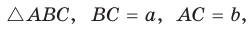
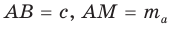 — медиана треугольника (рис. 170). Продлим медиану AM за точку М на ее длину:
— медиана треугольника (рис. 170). Продлим медиану AM за точку М на ее длину: 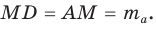
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 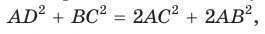
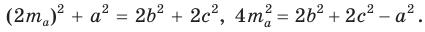 Отсюда следует, что
Отсюда следует, что 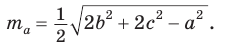
Утверждение доказано.
Аналогично: 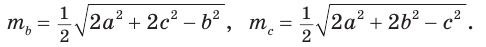
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 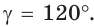 Найти сторону с. б) Дан треугольник АВС, а = 7, с = 8, а = 60°. Найти сторону Ь.
Найти сторону с. б) Дан треугольник АВС, а = 7, с = 8, а = 60°. Найти сторону Ь.
Решение:
а) По теореме косинусов 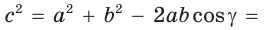
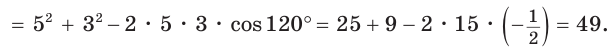 Отсюда
Отсюда 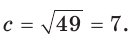 б) Пусть
б) Пусть 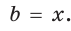 По теореме косинусов
По теореме косинусов 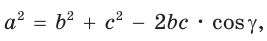 то есть
то есть 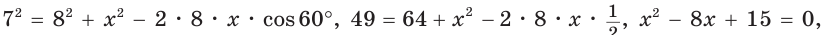
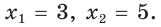 Отсюда
Отсюда 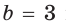 или
или 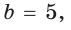 так как для наборов длин отрезков 7, 3, 8 и 7, 5, 8 выполняется неравенство треугольника.
так как для наборов длин отрезков 7, 3, 8 и 7, 5, 8 выполняется неравенство треугольника.
Ответ: а) 7; б) 3 или 5.
Пример:
Две стороны треугольника равны 6 и 10, его площадь — 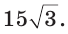
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в 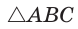 стороны АВ = 6, ВС = 10 и
стороны АВ = 6, ВС = 10 и 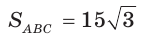 (рис. 171).
(рис. 171).
Поскольку 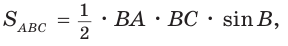 то
то 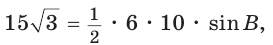 откуда
откуда 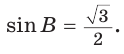
Так как 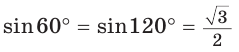 и по условию
и по условию 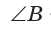 — тупой, то
— тупой, то  . Для нахождения стороны АС применим теорему косинусов:
. Для нахождения стороны АС применим теорему косинусов: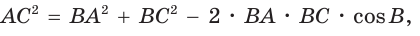
Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 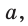
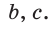 Пусть
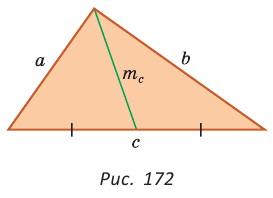
Пусть 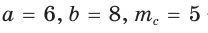 — медиана (рис. 172).
— медиана (рис. 172).
По формуле медианы 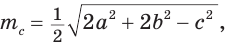 откуда
откуда 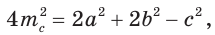
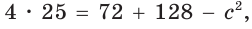
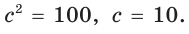 По обратной теореме Пифагора данный треугольник со сторонами 6, 8 и 10 — прямоугольный, его площадь равна половине произведения катетов:
По обратной теореме Пифагора данный треугольник со сторонами 6, 8 и 10 — прямоугольный, его площадь равна половине произведения катетов: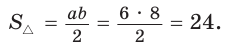
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 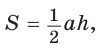 а также по двум сторонам и углу между ними:
а также по двум сторонам и углу между ними: 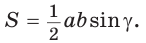 Теперь мы выведем формулу нахождения площади треугольника по трем сторонам.
Теперь мы выведем формулу нахождения площади треугольника по трем сторонам.
Теорема (формула Герона).
Площадь треугольника со сторонами 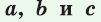 можно найти по формуле
можно найти по формуле 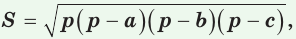 где
где 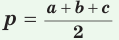 — полупериметр треугольника.
— полупериметр треугольника.
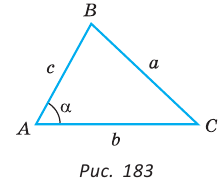
Доказательство:
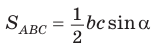 (рис. 183). Из основного тригонометрического тождества
(рис. 183). Из основного тригонометрического тождества 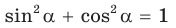 следует, что
следует, что 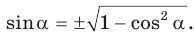 Для
Для 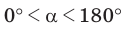 синус положительный. Поэтому
синус положительный. Поэтому 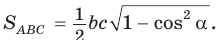 Из теоремы косинусов
Из теоремы косинусов 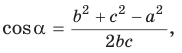 откуда
откуда 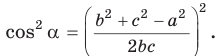
Тогда 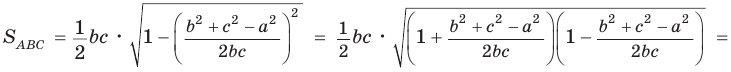
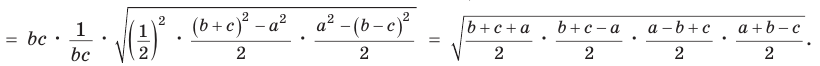
Так как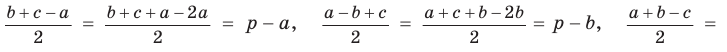
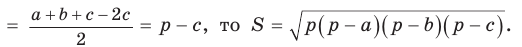 Теорема доказана.
Теорема доказана.
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
Пример №1 (решение треугольника по двум сторонам и углу между ними).
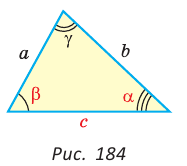
Дано: 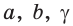 (рис. 184).
(рис. 184).
Найти : 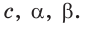
Решение:
Рис. 184
1) По теореме косинусов 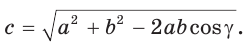
2) По следствию из теоремы косинусов 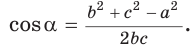
3) Угол 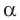 находим при помощи калькулятора или таблиц.
находим при помощи калькулятора или таблиц.
4) Угол 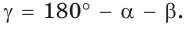
Замечание. Нахождение угла 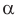 по теореме синусов
по теореме синусов 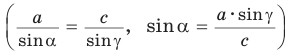 требует выяснения того, острый или тупой угол
требует выяснения того, острый или тупой угол 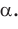
Пример №2 (решение треугольника по стороне и двум прилежащим к ней углам).
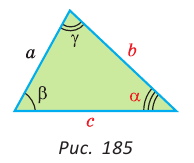
Дано: 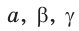 (рис. 185).
(рис. 185).
Найти: 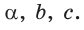
Решение:
1) Угол 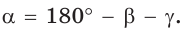
2) По теореме синусов 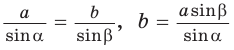 (sin
(sin 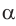 и sin
и sin 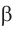 находим при помощи калькулятора или таблиц).
находим при помощи калькулятора или таблиц).
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 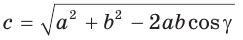 или
или 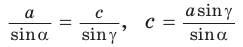 (cos
(cos 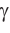 и sin
и sin 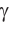 находим при помощи калькулятора или таблиц).
находим при помощи калькулятора или таблиц).
Пример №3 (решение треугольника по трем сторонам).
Дано: 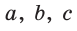 (рис. 186).
(рис. 186).
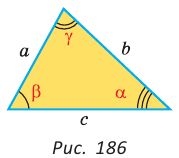
Найти: 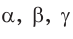 и радиус R описанной окружности.
и радиус R описанной окружности.
Решение:
1) По следствию из теоремы косинусов
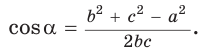
2) Зная  угол
угол 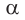 находим при помощи калькулятора или таблиц.
находим при помощи калькулятора или таблиц.
3) Аналогично находим угол 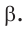
4) Угол 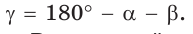
5) Радиус R описанной окружности треугольника можно найти по формуле 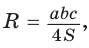 где
где 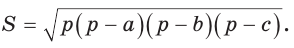
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 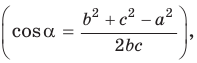 затем нахождение по косинусу угла его синуса
затем нахождение по косинусу угла его синуса 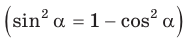 и, наконец, использование теоремы синусов
и, наконец, использование теоремы синусов 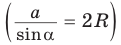 для нахождения R.
для нахождения R.
Пример №4
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим: 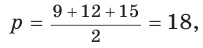
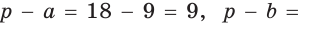
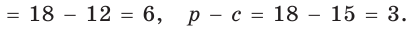 Тогда
Тогда 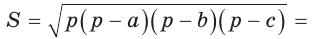
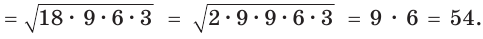 Радиус R описанной окружности найдем из формулы
Радиус R описанной окружности найдем из формулы 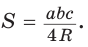 Имеем:
Имеем: 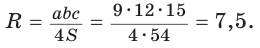
Ответ: 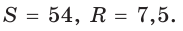
Способ 2. Так как 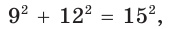 поскольку
поскольку 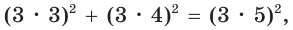 то треугольник — прямоугольный по обратной теореме Пифагора. Его площадь равна половине произведения катетов:
то треугольник — прямоугольный по обратной теореме Пифагора. Его площадь равна половине произведения катетов: 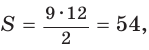 а радиус описанной окружности равен половине гипотенузы:
а радиус описанной окружности равен половине гипотенузы: 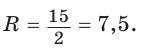
Пример №5
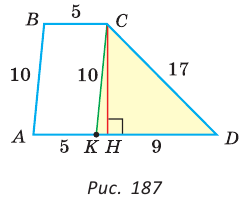
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 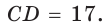 Проведем
Проведем 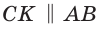 (рис. 187). Так как АВСК — параллелограмм, то СК = АВ = 10, АК = ВС = 5, откуда KD = AD – АК = 9. Найдем высоту СН треугольника KCD, которая равна высоте трапеции. Площадь треугольника KCD найдем по формуле Герона, обозначив его стороны а = 10, b = 17, с = 9. Получим:
(рис. 187). Так как АВСК — параллелограмм, то СК = АВ = 10, АК = ВС = 5, откуда KD = AD – АК = 9. Найдем высоту СН треугольника KCD, которая равна высоте трапеции. Площадь треугольника KCD найдем по формуле Герона, обозначив его стороны а = 10, b = 17, с = 9. Получим:
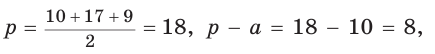
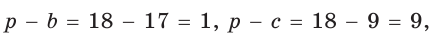
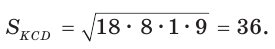 Так как
Так как 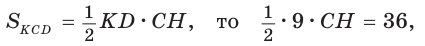 СН = 8. Площадь трапеции
СН = 8. Площадь трапеции 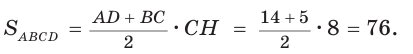
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
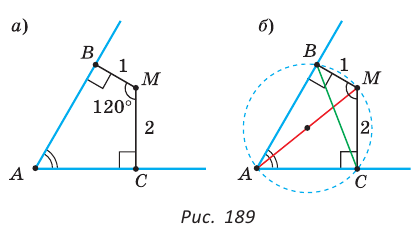
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 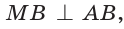
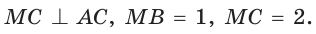 Найдем
Найдем
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому 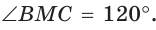
Так как в четырехугольнике АВМС 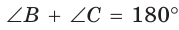 , то около него можно описать окружность по признаку вписанного четырехугольника (рис. 189, б). Поскольку прямой вписанный угол опирается на диаметр, то отрезок AM — диаметр этой окружности, т. е.
, то около него можно описать окружность по признаку вписанного четырехугольника (рис. 189, б). Поскольку прямой вписанный угол опирается на диаметр, то отрезок AM — диаметр этой окружности, т. е. 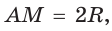 где R — радиус. Из
где R — радиус. Из 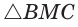 по теореме косинусов
по теореме косинусов 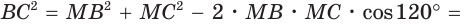
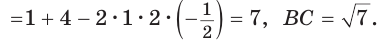 Из
Из 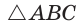 по теореме синусов
по теореме синусов 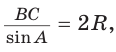 откуда
откуда 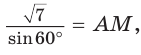
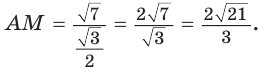
Ответ: 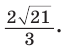
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Пример №6
В прямоугольном треугольнике АВС известно: 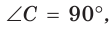
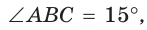 высота СН = 2 (рис. 190). Найти гипотенузу АВ.
высота СН = 2 (рис. 190). Найти гипотенузу АВ.
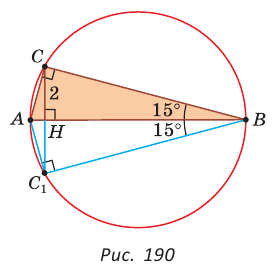
Решение:
Построим 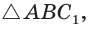 симметричный
симметричный 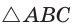 относительно прямой АВ (см. рис. 190).
относительно прямой АВ (см. рис. 190).
Поскольку 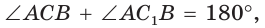 то вокруг четырехугольника
то вокруг четырехугольника 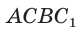 можно описать окружность, где АВ — диаметр этой окружности (прямой вписанный угол опирается на диаметр). Треугольник
можно описать окружность, где АВ — диаметр этой окружности (прямой вписанный угол опирается на диаметр). Треугольник 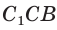 вписан в эту окружность,
вписан в эту окружность, 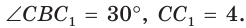 По теореме синусов
По теореме синусов 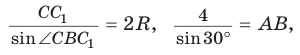 откуда
откуда 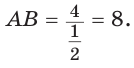
Ответ: 8.
Пример №7
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 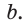 На гипотенузе АВ как на стороне построен квадрат ADFB (рис. 191). Найти расстояние от центра О этого квадрата до вершины С прямого угла, т. е. отрезок СО.
На гипотенузе АВ как на стороне построен квадрат ADFB (рис. 191). Найти расстояние от центра О этого квадрата до вершины С прямого угла, т. е. отрезок СО.
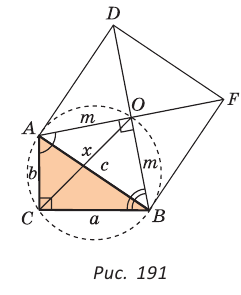
Решение:
Способ 1. Так как 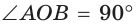 (диагонали квадрата ADFB взаимно перпендикулярны), то
(диагонали квадрата ADFB взаимно перпендикулярны), то 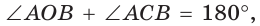 поэтому четырехугольник АОВС является вписанным в окружность, ее диаметр
поэтому четырехугольник АОВС является вписанным в окружность, ее диаметр 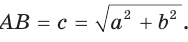 Тогда
Тогда 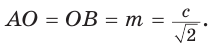
Пусть СО = х. По теореме косинусов из 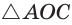 находим
находим 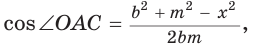
из 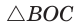 находим
находим 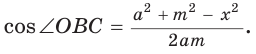
По свойству вписанного четырехугольника 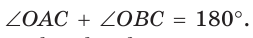 Поскольку
Поскольку 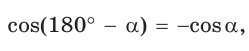 то
то 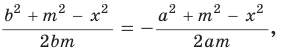 откуда находим
откуда находим 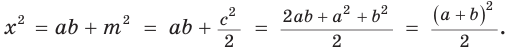 Тогда
Тогда 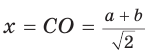 .
.
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
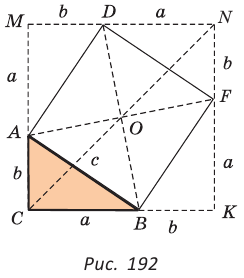
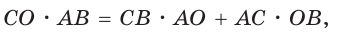
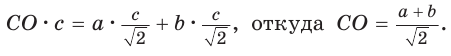
Способ 3. Достроим 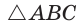 до квадрата CMNK, как показано на рисунке 192. Можно показать, что центр квадрата CMNK совпадет с центром квадрата ADFB, т. е. с точкой О (точки В и D симметричны относительно центров обоих квадратов). Тогда
до квадрата CMNK, как показано на рисунке 192. Можно показать, что центр квадрата CMNK совпадет с центром квадрата ADFB, т. е. с точкой О (точки В и D симметричны относительно центров обоих квадратов). Тогда 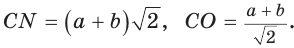
Ответ: 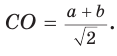
Пример №8
Точка О — центр окружности, вписанной в треугольник АВС, 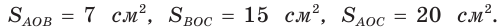 Найти стороны треугольника (см. задачу 232*).
Найти стороны треугольника (см. задачу 232*).
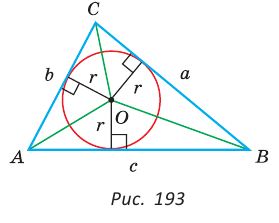
Решение:
Пусть 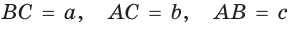 и
и
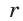 — радиус вписанной окружности (рис. 193).
— радиус вписанной окружности (рис. 193).
Тогда 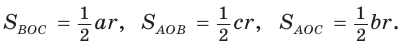
Отсюда 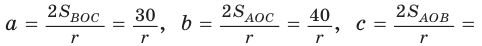
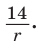 Применим формулу Герона:
Применим формулу Герона:
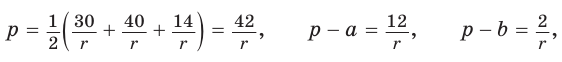
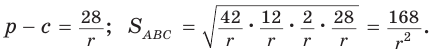
С другой стороны, 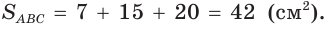 Из уравнения
Из уравнения 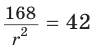 находим
находим 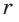 = 2. Откуда
= 2. Откуда 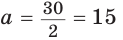 (см),
(см), 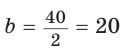 (см),
(см), 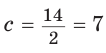 (см).
(см).
Ответ: 15 см; 20 см; 7 см.
Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
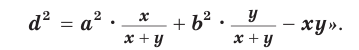
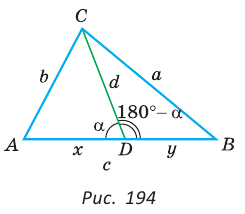
Доказательство:
По теореме косинусов из 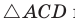 и
и 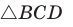 (см. рис. 194) следует:
(см. рис. 194) следует:
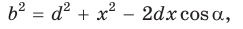 (1)
(1)
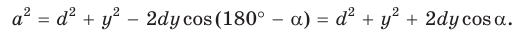 (2)
(2)
Умножим обе части равенства (1) на у, равенства (2) — на 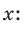
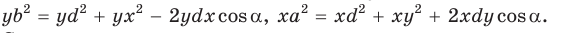
Сложим почленно полученные равенства:
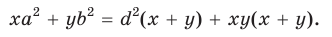
Из последнего равенства выразим 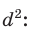
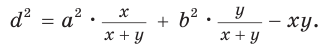 Теорема доказана.
Теорема доказана.
Следствие:
Биссектрису треугольника можно найти по формуле (рис. 195)
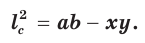
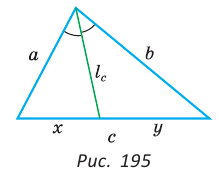
Доказательство:
По свойству биссектрисы треугольника 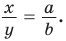 Разделив сторону
Разделив сторону 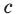 с в отношении
с в отношении 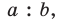 получим:
получим:
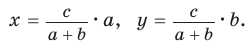 По теореме Стюарта
По теореме Стюарта 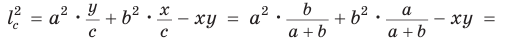
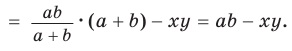
Пример №9
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
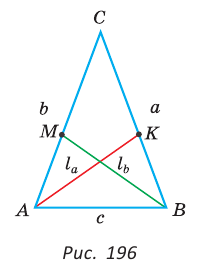
Пусть дан треугольник АВС, 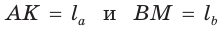 — биссектрисы, проведенные к сторонам ВС = а и АС = b соответственно, и
— биссектрисы, проведенные к сторонам ВС = а и АС = b соответственно, и 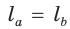 (рис. 196). Нужно доказать, что
(рис. 196). Нужно доказать, что 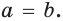 Выразим
Выразим 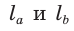 и через
и через 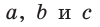 и приравняем полученные выражения. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому
и приравняем полученные выражения. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому 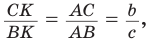 откуда
откуда 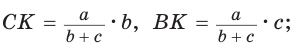
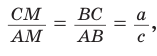 откуда
откуда 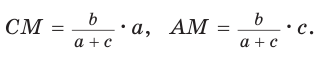
По формуле биссектрисы треугольника 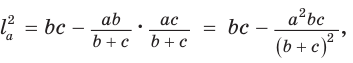
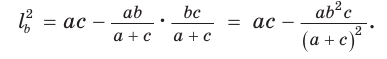
Из условия 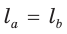 следует:
следует: 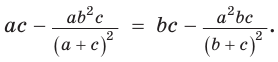 Перенеся слагаемые в одну сторону равенства и разложив на множители (проделайте это самостоятельно), получим:
Перенеся слагаемые в одну сторону равенства и разложив на множители (проделайте это самостоятельно), получим: 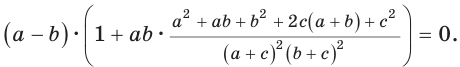 Отсюда
Отсюда 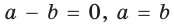 (второй множитель при положительных
(второй множитель при положительных 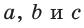 больше нуля). Утверждение доказано.
больше нуля). Утверждение доказано.
Теорема Птолемея о вписанном четырехугольнике
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е.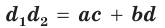 (рис. 197).
(рис. 197).
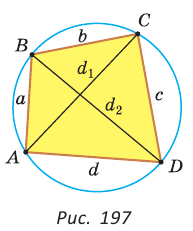
Доказательство:
Из 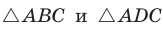 по теореме косинусов
по теореме косинусов 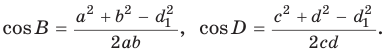
Так как 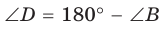 (по свойству вписанного четырехугольника) и
(по свойству вписанного четырехугольника) и 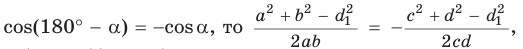 откуда
откуда 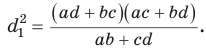
Аналогично из 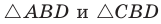 получим
получим 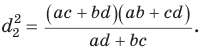 Тогда
Тогда 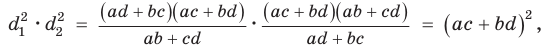
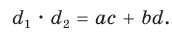 Теорема доказана.
Теорема доказана.
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
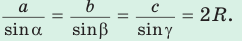
- Радиус описанной окружности треугольника можно найти, используя формулы:
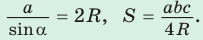
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
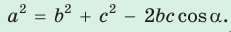
- Пусть
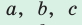 — стороны треугольника и с — большая сторона. Если
— стороны треугольника и с — большая сторона. Если 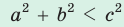 , то треугольник тупоугольный, если
, то треугольник тупоугольный, если 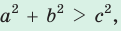 то треугольник остроугольный, если
то треугольник остроугольный, если 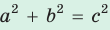 , то треугольник прямоугольный.
, то треугольник прямоугольный. - Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
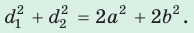
- Формула Герона:
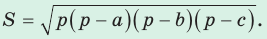
- Формула медианы:
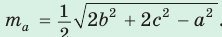
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Как найти стороны прямоугольника, если известна диагональ
Прямоугольник – плоская фигура, у которой стороны попарно равны и параллельны. Диагонали прямоугольника тоже одинаковые. Одна диагональ делит исходную фигуру на два прямоугольных треугольника с острыми углами по сорок пять градусов. Исходя из этих данных можно легко найти стороны прямоугольника, зная только численное значение диагонали.

Инструкция
Для нахождения сторон прямоугольника нужно рассмотреть один из тех самых прямоугольных треугольников. В нем гипотенуза является диагональю прямоугольника, а катеты – его сторонами. Перед непосредственным вычислением с числовыми значениями нужно найти уравнения в общем виде. Для каждой стороны будет свое уравнение. Итак, для получения формул, в прямоугольном треугольнике обозначьте катеты латинскими буквами а и b, а гипотенузу – с.
Решение задачи заключается в определении синуса и теоремы Пифагора. Выберите любой из острых углов в треугольнике (они равны), с которым будете работать. Определите прилежащий к нему катет и, противолежащий от него, другой катет. Например, пусть, прилежащим к углу, будет катет b, а находящимся напротив – катет а.
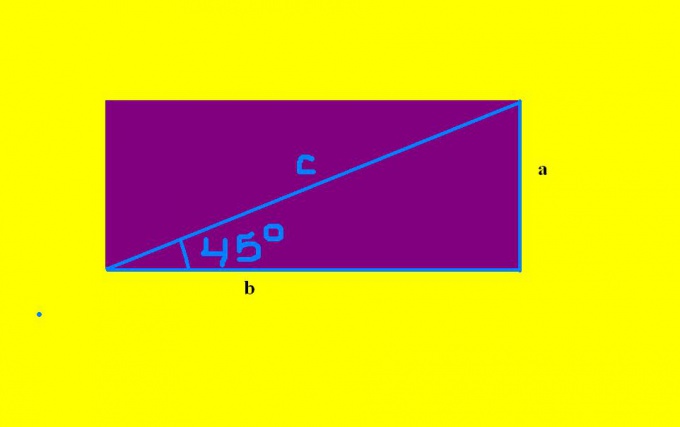
Далее, исходя из определения синуса, которое гласит, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, составьте уравнение: sin 45 = а/с. В данном примере, по условию, известны: синус угла (sin 45 ~0,7) и гипотенуза с. Отсюда, получается уравнение 0,7=а/с, из которого а=0,7с. Осталось подставить численное значение с. Найденная сторона а будет равна параллельной стороне в прямоугольнике. Таким образом, известны две стороны фигуры.
Источники:
- Геометрия 7-9 классы. Погорелов. Просвещение 2010 год.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Параллелограммом называют четырёхугольный многоугольник, две соседние стороны которого равны и
параллельны противоположным. Помимо этого, есть ещё несколько важных условий определения фигуры как
параллелограмма:
- В месте пересечения диагонали делятся пополам, а точка, в которой пересекаются диагонали,
является одновременно центром этих двух отрезков. При этом она всегда лежит внутри фигуры. - Любая диагональ данного четырёхугольника разделяет его на одинаковые треугольники, так как
проходит из одной вершины к противоположной, то есть по центру четырёхугольника. - Сумма квадратов сторон равна сумме квадратов диагоналей.
- Углы фигуры, расположенные друг напротив друга, попарно равны. Это условие вытекает из
утверждения, что параллельные стороны фигуры равны. - Сумма двух односторонних углов равна 180°. Это условие напрямую связано с теоремой о двух
параллельных прямых и секущей. И действительно, если рассматривать две противоположные и третью
между ними стороны параллелограмма как две параллельные прямые и секущую, то можно заметить, что
углы, принадлежащие одной стороне, будут соответствовать односторонним углам, сумма которых,
согласно теореме, равна 180°.
Только при выполнении всех условий четырёхугольный многоугольник будет считаться
параллелограммом.
- Длинная сторона параллелограмма через две диагонали и
острый угол между ними - Длинная сторона параллелограмма через две диагонали и тупой
угол между ними - Короткая сторона параллелограмма через две диагонали и
острый угол между ними - Короткая сторона параллелограмма через две диагонали и
тупой угол между ними - Сторона параллелограмма через две диагонали и другую
известную сторону - Сторона параллелограмма через высоту и синус угла
- Сторона параллелограмма через площадь и высоту
Нахождение длинной стороны через две диагонали и острый угол между ними
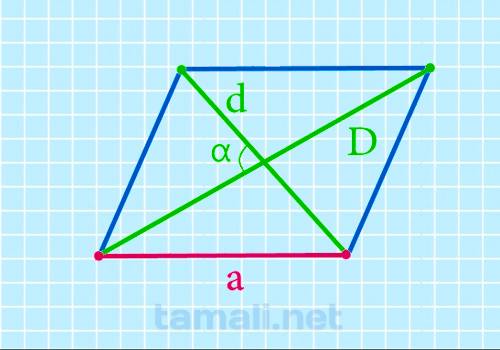
Длинную сторону параллелограмма можно найти, зная обе диагонали и острый угол между ними, по
формуле:
a = (√(D² + d² — 2 (D * d) * cosα)) / 2
где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Допустим, дан параллелограмм, у которого диагонали 7 и 4 см, а угол между
ними 68º. Тогда, согласно формуле, сторона будет равна: a = (√(7² + 4² — 2 (7 * 4) * cos68º)) / 2 = 3,317 см. Ответ:
3,317 см.
Нахождение короткой стороны через две диагонали и острый угол между ними
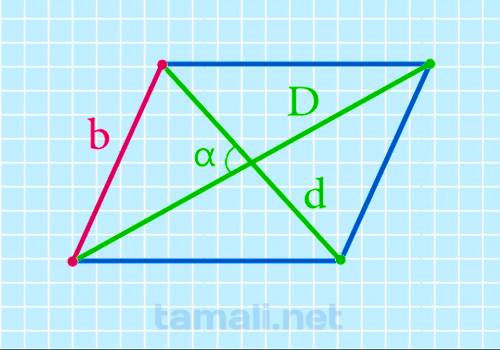
Можно вычислить и короткую сторону по формуле:
b = (√(D² + d² + 2 (D * d) * cosα)) / 2
где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Теперь необходимо найти другую сторону параллелограмма. Данные останутся те
же, что и в прошлой задаче, но в уравнении поменяется знак, так как по отношению к углу поменялась
сторона, которую надо найти. Сторона b будет равна: b = (√(7² + 4² + 2 (7 * 4) * cos68º)) / 2 = 4.64.
Ответ: 4,64 см.
Нахождение длинной стороны через две диагонали и тупой угол между ними
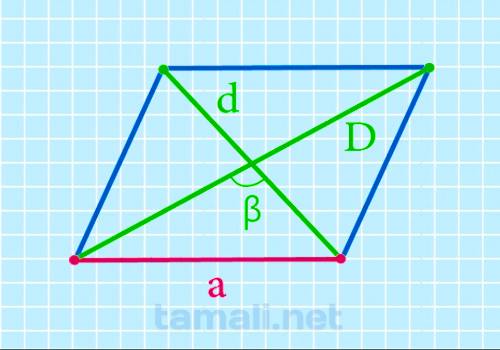
Стороны параллелограмма можно найти, зная диагонали и тупой угол между ними. Для этого нужно
использовать следующую формулу:
a = (√(D² + d² + 2 (D * d) * cosβ)) / 2
где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим нахождение сторон всё того же параллелограмма с диагоналями 7 и 4
см. Однако на этот раз возьмём между диагоналями другой угол: β=112º. В таком случае для стороны a
минус меняется на плюс, а сама сторона равна: a = (√(7² + 4² + 2 (7 * 4) * cos112º)) / 2 = 3.914
Нахождение короткой стороны через две диагонали и тупой угол между ними
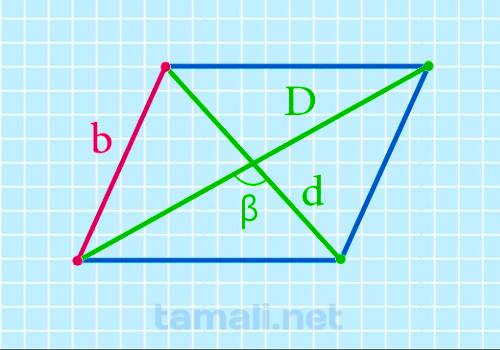
Аналогично можно найти и короткую сторону, зная диагонали и тупой угол между ними:
b = (√(D² + d² — 2 (D * d) * cosβ)) / 2
где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Для стороны b так же изменится знак в формуле, но наоборот: плюс на минус. Тогда
получается: b = (√(7² + 4² — 2 (7 * 4) * cos112)) / 2 = 4,64 см. Ответ совпал с ответом второй
задачи, все опять решено верно, а сторона в воображаемом параллелограмме действительно равна 4,64
см.
Нахождение стороны параллелограмма через диагонали и другую сторону
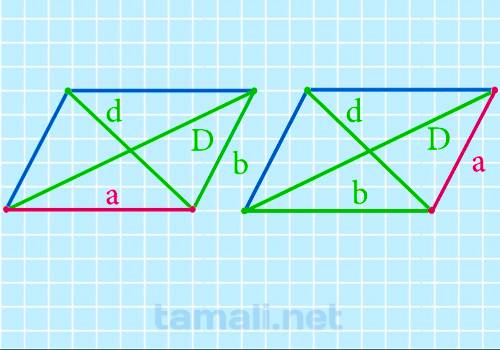
Как и в случае с прошлыми пунктами, существуют формула, которая позволяет найти сторону
параллелограмма с использованием диагоналей и известной стороны. Вот она:
a = √(D² + d² — 2b² / 2)
где D, d — диагонали, b — сторона.
Цифр после
запятой:
Результат в:
Выводится данная формулы из первого следствия теоремы косинусов.
Пример. Используем для следующих задач другой параллелограмм. Эта фигура будет с
диагоналями 9 и 5 см и стороной 6 см. Тогда другая сторона данного параллелограмма равна: a = √(9² + 5² — 2 * 6² / 2) = 4,1 см. Ответ: 4,1 см.
Для проверки ответа можем решить обратную задачу, при которой нам не известна сторона b, но известна
сторона a = 4,1 см. По обратной формуле получается b = √(9² + 5² — 2 * 4,1² / 2) = 6 см. Ответ
совпадает с изначальными данными первой задачи. А значит и этот воображаемый параллелограмм
действительно существует.
Нахождение стороны через синус угла и высоту
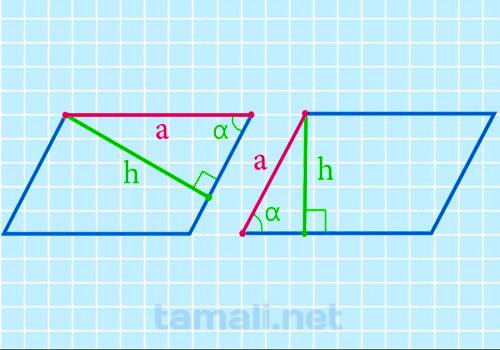
Высота – это отрезок, опущенный перпендикулярно из вершины фигуры на противоположную сторону. Есть
несколько интересных свойств у неё. Например, высоты, проведенные из острых углов, будут всегда
лежать вне фигуры, в то время как высоты из тупых углов всегда лежат внутри. Если из одного угла
опустить две высоты, то между ними образуется угол, равный смежному углу параллелограмма. Равными
будут те высоты, что заключены между параллельными сторонами четырёхугольника. Найти сторону
параллелограмма через эту величину достаточно просто, по формуле:
a = h / sinα
где: h — высота параллелограмма, sin α — угол.
Цифр после
запятой:
Результат в:
Стоит заметить, что высота должна быть опущена не к искомой стороне, а к соседней. При этом для
формулы сойдет синус любого известного угла параллелограмма.
Пример. Найти сторону параллелограмма, если высота, опущенная на соседнюю сторону
равна 10 см, а острый угол — 30º. Решение: a=10 / 0,5 = 20 см
Нахождение стороны через площадь и высоту
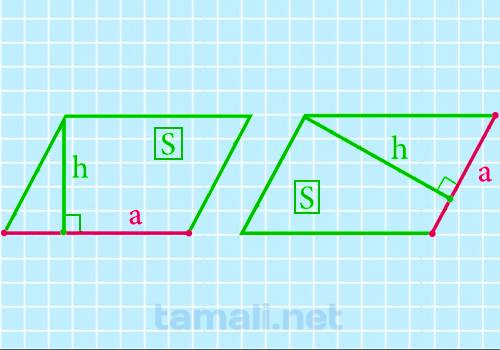
Более подробно о площади и высоте параллелограмма рассказано в пунктах выше. В этом достаточно легко
вывести единственную формулу, по которой можно найти сторону. Если площадь является произведением
стороны на высоту, то сторона будет равна отношению площади к высоте:
a = S / h
где S — площадь параллелограмма, h — высота.
Цифр после
запятой:
Результат в:
Причем не имеет значения, к какой стороне опущена высота: к искомой или соседней.
Пример. Найти сторону параллелограмма, если его площадь равна 20 см, а высота,
опущенная на одну из сторон — 5 см. Решение: a = 20 / 5 = 4 см.
Фигура кажется сложной для восприятия из-за того, что её нельзя постоянно наблюдать где-то в
повседневной жизни. Однако всё становится проще, если вспомнить, что есть более известные широкой
публике частные случаи параллелограмма. Их-то человек обычно наблюдает ежедневно. Это ромб,
прямоугольник и квадрат. Причем последний, хоть и наиболее известен, является и наиболее
интересным.
Ромб считается частным случаем, потому что представляет собой параллелограмм, диагонали которого в
точке пересечения образуют прямой угол. Прямоугольник является частным случаем, потому что это
параллелограмм, у которого все углы прямые. У квадрата же положение ещё интереснее, так как его
можно назвать не только частным случаем параллелограмма, но и прямоугольника, и ромба. Квадрат – это
комбо трёх предыдущих определений. Можно даже сказать, что квадрат одновременно является особенным
случаем и для параллелограмма, и для прямоугольника, и для ромба. Все его стороны равны,
противоположные стороны параллельны. Все углы являются прямыми, даже образующиеся при пересечении
диагоналей, которые к тому же делятся пополам в точке пересечения.
