|
Площадь – 56 квадратных см. Периметр – 30 см.
Сторона А=7, сторона В=8 S=AxB P=2A+2B S=56 P=30 автор вопроса выбрал этот ответ лучшим Можно попробовать решить данную задачу, составив систему уравнений. Периметр прямоугольника равен: p=2a+2b; Площадь прямоугольника равна: s=a*b; Так как мы знаем периметр и площадь, то сразу подставляем числа: 30=2a+2b; 56=a*b; Выражаем b через a во втором уравнении: b=56/a; И подставляем 56/a вместо b в первое уравнение: 30=2a+2(56/a); 15=a+56/a; Домножаем обе части на a: 15a=a²+56; Получаем квадратное уравнение: a²-15a+56=0; Находим корни этого квадратного уравнения: (15±√(15²-4*1*56))/2*1 = (15±√(225-224))/2 = (15±√1)/2 = (15±1)/2 Получилось, что корни этого уравнения: a1=(15+1)/2=16/2=8; a2=(15-1)/2=14/2=7; Получается, что у нас 2 возможных варианта прямоугольников. Вспомним, что мы выразили: b=56/a; Отсюда находим возможные b: b1=56/a1=56/8=7; b2=56/a2=56/7=8; Как оказалось эти два разных прямоугольника – это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно: Если a=7 и b=8. Либо наоборот: a=8 и b=7. То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот – горизонтальная больше вертикальной. Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.
Oleg74 9 лет назад Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны : а – одна сторона, в – другая сторона прямоугольника. S = а * в P = 2а + 2в Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см. а = 7 см в = 8 см. Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее S = а*b P = 2(а+b) получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади
Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот. Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник; если дискриминант равен нолю – тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5); если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 – решения нет)
Galina7v7 7 лет назад Дано: S = 56 смР = 30 смСтороны=?Решение:Пусть стороны прямоугольника a и b. Тогда: площадь S = a * b , периметр Р=2*(a + b), Получим систему уравнений: {a*b=56 ? {ab=56 {2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение: b=15-a, a^2 -15a +56 =0 ,решая которое ,получим : a1=7, a2=8, b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7.
Zolotynka 7 лет назад Нашла еще такое решение, Известно, что периметр прямоугольника 30 а площадь 56, далее: периметр = 2*(длина + ширина) или 2L + 2W площадь= длина * ширина или L * W 2L + 2W = 30 (делим обе части на 2) L + W = 15 L * W = 56 L * (15 – L) = 56 Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется.
Azamatik 7 лет назад Вспоминаем школьную геометрию: Периметр прямоугольника – это будет сумма длин всех сторон, а площадь прямоугольника – это уже произведение двух смежных его сторон (длину на ширину). В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно. Итак, решение: S – площадь = а x b; 56 = a x b; Р – периметр = а + b + a + b = 2a + 2b; 30 = 2 (а + b); 15 = a + b; a = 15 – b; Делаем подставление: 56 = (15 – b) x b; 56 = 15 b – b^2; b^2 – 15b + 56 = 0. Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7. Находим и другую сторону прямоугольника: a1 = 15 – 8 = 7; a2 = 15 – 7 = 8. Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см.
Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь.Это выглядит так А=S/В=56/В Затем подставляем это выражение вместо буквы А в уравнении для периметра: Р=2(56/В + В)=30 Получаем что 56/В+В=15 В этом уравнении даже решать его не надо – любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника.
Хеленочка 8 лет назад Обозначим одну сторону буквой Х, другую – буквой Y. Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение: Х*Y=56 Периметр – это сумма длин сторон, следовательно, второе уравнение такое: 2Х+2Y=30 Получаем систему двух уравнений. По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение: 2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8. Lilechka 9 лет назад Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения: (а+c)х2=30 ахс=56 Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см.
moreljuba 7 лет назад Итак, для начала рассмотрим формулы для нахождения площади и периметра: 1) S = a * b = 56 см2; 2) Р = 2а + 2b = 30 см. Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны. Таким образом нам требуется решить систему из двух уравнений: a * b = 56 2а + 2b = 30 Отсюда получаем, что одна сторона равна 7, а другая 8. Знаете ответ? |
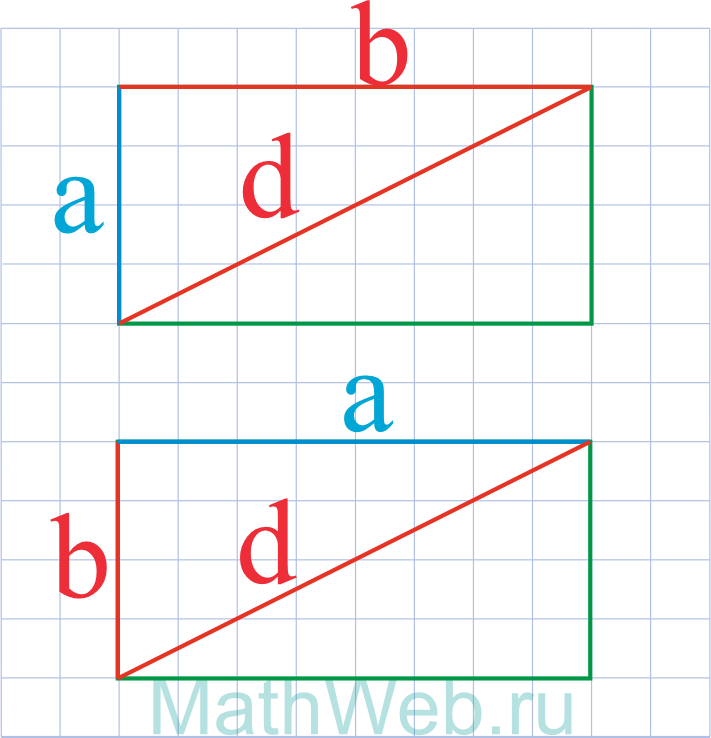
Где d – диагональ,b – сторона.
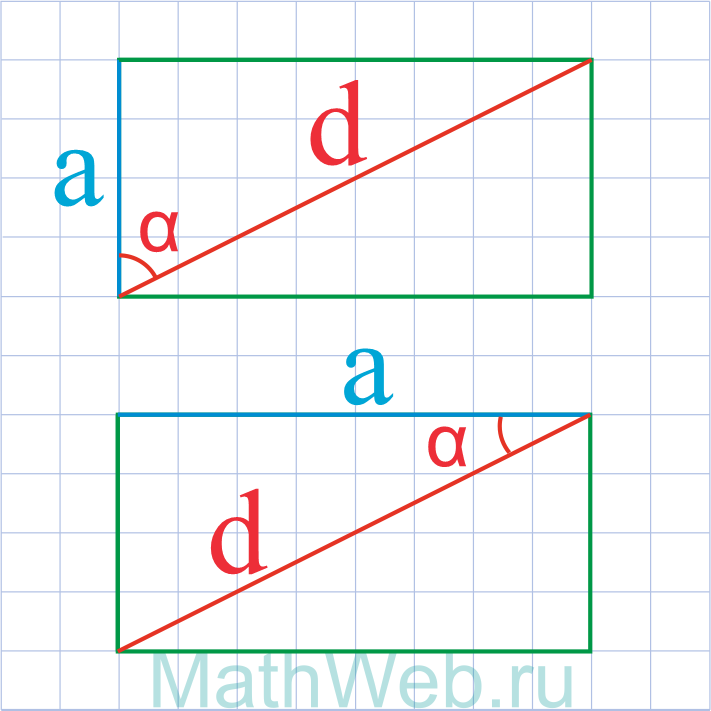
Где d – диагональ,α – угол между диагональю и искомой стороной.
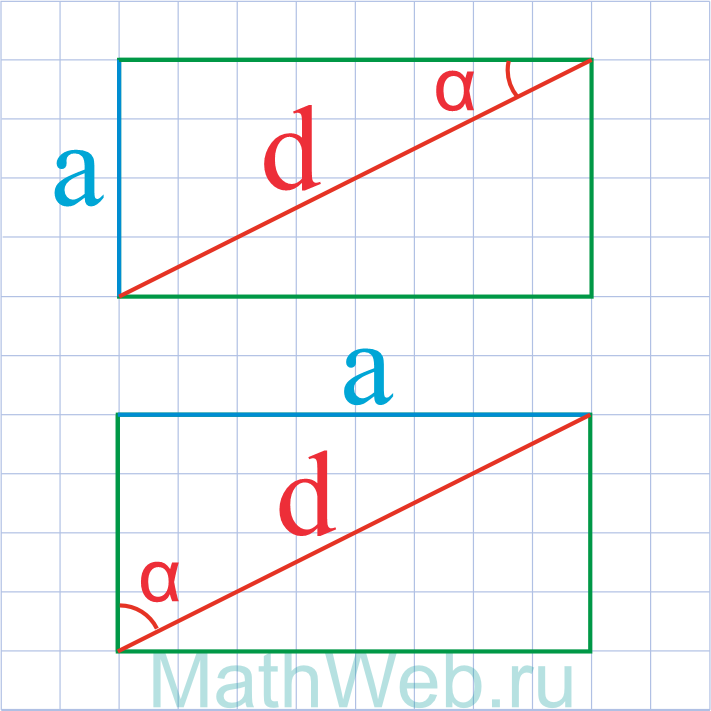
Где d – диагональ,α – угол между диагональю и другой стороной.
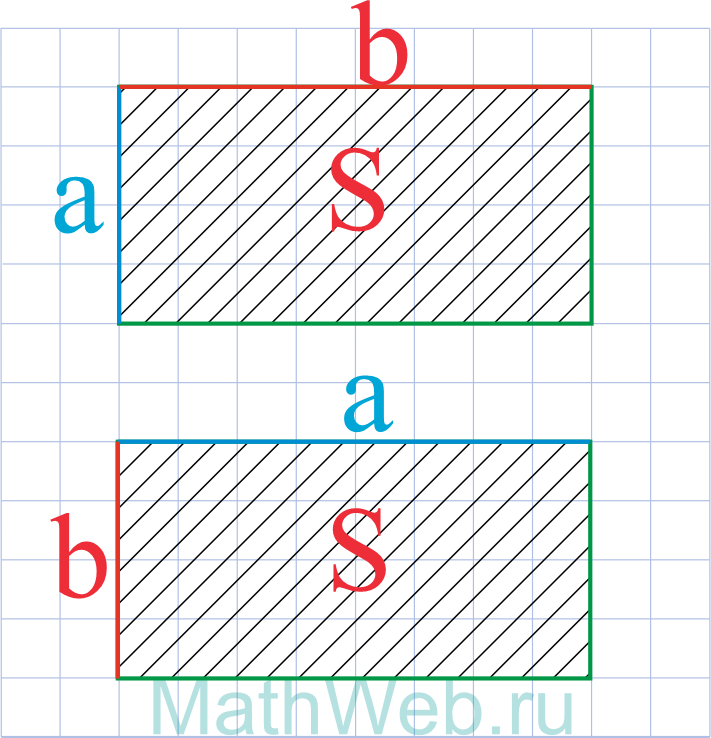
Где S – площадь, b– известная сторона.
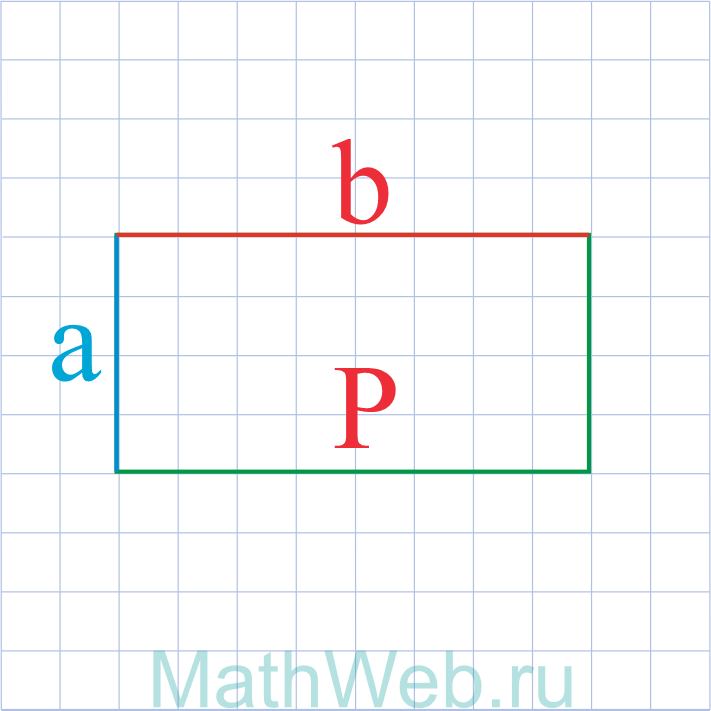
Где P – периметр, b – известная сторона.
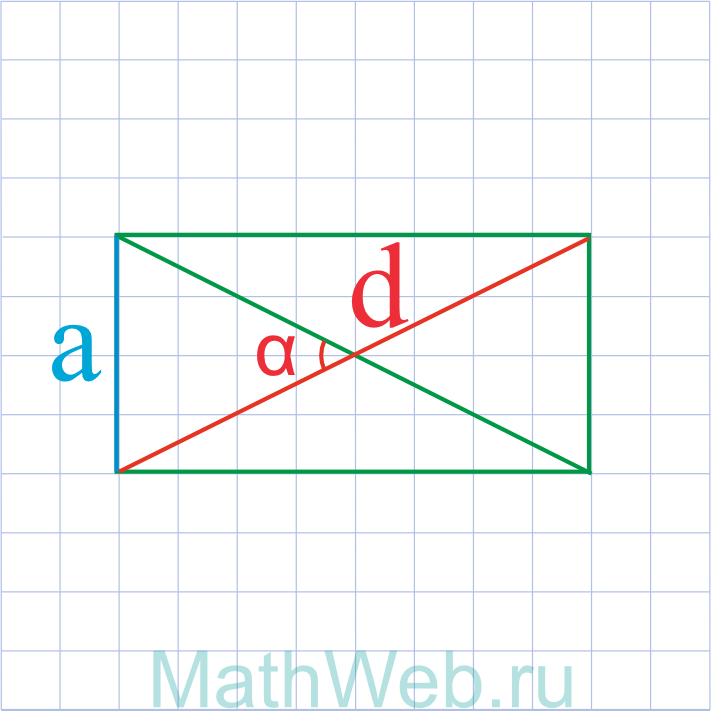
Где d – диагональ, α – угол между диагоналями.
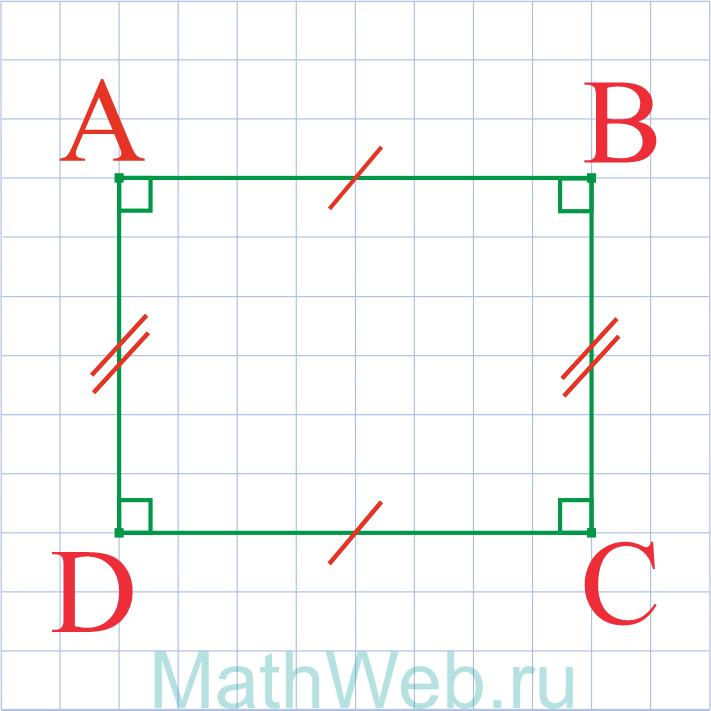
- Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = √d2 ― b2 |
 |
a = d·cos(α) |
 |
a = d·sin(α) |
 |
a = S b |
 |
a = P – 2b 2 |
 |
a = d·sin(0.5·α) |
Зная в прямоугольнике площадь и сторону можно найти вторую сторону, и затем все остальные параметры по порядку. Вторая сторона прямоугольника будет равна отношению площади к известной стороне.
b=S/a
Для того чтобы найти периметр прямоугольника через площадь и сторону, необходимо подставить в формулу вместо второй стороны полученное отношение
P=2(a+b)=2(a+S/a)
Диагональ прямоугольника можно найти через теорему Пифагора в прямоугольном треугольнике, который она образует. Обе диагонали прямоугольника принимают одно и то же значение. Выразив b через площадь и известную сторону, получим следующее выражение. (рис. 56.1)
d_1=d_2=√(a^2+b^2 )=√(a^2+(S/a)^2 )=√(a^2+S^2/a^2 )
Используя тригонометрические отношения в полученном треугольнике можно найти углы при пересечении диагоналей со сторонами. Для этого проще всего будет использовать тангенс, как отношение катетов друг к другу. Точно также, как и в предыдущих формулах, заменяем неизвестную сторону на равное ей выражение.
α=arc tan〖b/a〗=arc tan〖S/a^2 〗
β=arc tan〖a/b=arc tan〖a^2/S〗 〗
Угол, образованный при пересечении диагоналей, и дополнительный ему до 180° зависят только от углов при диагонали и стороне, и равны удвоенному их значению. (рис. 56.2)
γ=2α
δ=2β
Радиус описанной вокруг прямоугольника окружности равен половине диагонали, так как лежит на ней и исходит из точки пересечения диагоналей. (рис. 56.3)
R=d/2=√(a^2+S^2/a^2 )/2
Сторона прямоугольника по площади и другой стороне в м

Введите длину стороны a в м:
0.00м
S = a • b ⇒ b = S : a
S — площадь прямоугольника в м2 (квадратных метрах);
a — известная длина одной из сторон прямоугольника в м (метрах).
b — неизвестная длина другой стороны прямоугольника в м (метрах)
Например:
Площадь прямоугольника равна 192 м2, одна сторона равна 8 м. Найдите длину другой стороны прямоугольника.
Краткое решение: b = S : a = 192 : 8 = 24 м.
Площадь прямоугольника равна 144 м2, длина прямоугольника равна 18 м. Найдите его ширину.
Краткое решение: ширина прямоугольника b = S : a = 144 : 18 = 8 м.
Как найти стороны прямоугольника, если знаем общую длину и площадь?
Анонимный вопрос
11 февраля 2020 · 15,1 K
Площадь прямоугольник это:
S=a*b (произведение его сторон).
Общая длина, как я понял, это его периметр, который равен:
P=2(a+b). Из них составляем систему уравнений
S=ab;
P=2(a+b). Выражаем одну из сторон из какого-либо уравнения, поставляем её в оставшееся уравнение, из которого находим вторую сторону и уже зная её находим первую сторону. Например можно сделать так… Из первого уравнения выражаем сторону a, получим:
a=S/b. Подставляем её во второе уравнение получим:
P=2((S/b)+b) <=> (выражаем b) 2(S+b²)/b = P <=> b = (P+√[P²-16S])/4. Тогда сторона a будет ровна:
a=4S/(P+√[P²-16S]), а тогда сторону b можно натйи из той же системы: подставим выраженную сторону a, к примеру, в выражение площади, тогда выражение для стороны b примет вид
b = (P+√[P²-16S])/4.
10,1 K
Комментировать ответ…Комментировать…


