|
Площадь – 56 квадратных см. Периметр – 30 см. Сторона А=7, сторона В=8 S=AxB P=2A+2B S=56 P=30 автор вопроса выбрал этот ответ лучшим Можно попробовать решить данную задачу, составив систему уравнений. Периметр прямоугольника равен: p=2a+2b; Площадь прямоугольника равна: s=a*b; Так как мы знаем периметр и площадь, то сразу подставляем числа: 30=2a+2b; 56=a*b; Выражаем b через a во втором уравнении: b=56/a; И подставляем 56/a вместо b в первое уравнение: 30=2a+2(56/a); 15=a+56/a; Домножаем обе части на a: 15a=a²+56; Получаем квадратное уравнение: a²-15a+56=0; Находим корни этого квадратного уравнения: (15±√(15²-4*1*56))/2*1 = (15±√(225-224))/2 = (15±√1)/2 = (15±1)/2 Получилось, что корни этого уравнения: a1=(15+1)/2=16/2=8; a2=(15-1)/2=14/2=7; Получается, что у нас 2 возможных варианта прямоугольников. Вспомним, что мы выразили: b=56/a; Отсюда находим возможные b: b1=56/a1=56/8=7; b2=56/a2=56/7=8; Как оказалось эти два разных прямоугольника – это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно: Если a=7 и b=8. Либо наоборот: a=8 и b=7. То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот – горизонтальная больше вертикальной. Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.Oleg74 9 лет назад Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны : а – одна сторона, в – другая сторона прямоугольника. S = а * в P = 2а + 2в Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см. а = 7 см в = 8 см. Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее S = а*b P = 2(а+b) получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот. Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник; если дискриминант равен нолю – тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5); если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 – решения нет) Galina7v7 7 лет назад Дано: S = 56 смР = 30 смСтороны=?Решение:Пусть стороны прямоугольника a и b. Тогда: площадь S = a * b , периметр Р=2*(a + b), Получим систему уравнений: {a*b=56 ? {ab=56 {2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение: b=15-a, a^2 -15a +56 =0 ,решая которое ,получим : a1=7, a2=8, b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7. Zolotynka 7 лет назад Нашла еще такое решение, Известно, что периметр прямоугольника 30 а площадь 56, далее: периметр = 2*(длина + ширина) или 2L + 2W площадь= длина * ширина или L * W 2L + 2W = 30 (делим обе части на 2) L + W = 15 L * W = 56 L * (15 – L) = 56 Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется. Azamatik 7 лет назад Вспоминаем школьную геометрию: Периметр прямоугольника – это будет сумма длин всех сторон, а площадь прямоугольника – это уже произведение двух смежных его сторон (длину на ширину). В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно. Итак, решение: S – площадь = а x b; 56 = a x b; Р – периметр = а + b + a + b = 2a + 2b; 30 = 2 (а + b); 15 = a + b; a = 15 – b; Делаем подставление: 56 = (15 – b) x b; 56 = 15 b – b^2; b^2 – 15b + 56 = 0. Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7. Находим и другую сторону прямоугольника: a1 = 15 – 8 = 7; a2 = 15 – 7 = 8. Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см. Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь.Это выглядит так А=S/В=56/В Затем подставляем это выражение вместо буквы А в уравнении для периметра: Р=2(56/В + В)=30 Получаем что 56/В+В=15 В этом уравнении даже решать его не надо – любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника. Хеленочка 8 лет назад Обозначим одну сторону буквой Х, другую – буквой Y. Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение: Х*Y=56 Периметр – это сумма длин сторон, следовательно, второе уравнение такое: 2Х+2Y=30 Получаем систему двух уравнений. По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение: 2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8. Lilechka 9 лет назад Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения: (а+c)х2=30 ахс=56 Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см. moreljuba 7 лет назад Итак, для начала рассмотрим формулы для нахождения площади и периметра: 1) S = a * b = 56 см2; 2) Р = 2а + 2b = 30 см. Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны. Таким образом нам требуется решить систему из двух уравнений: a * b = 56 2а + 2b = 30 Отсюда получаем, что одна сторона равна 7, а другая 8. Знаете ответ? |
Расчет площади геометрических фигур — это базовый навык, необходимый в математике, инженерии, архитектуре и других науках. Однако, на практике возникает необходимость не только вычислять площадь фигуры, но и находить зависимости, например, между площадью и другими характеристиками фигуры. В этой статье мы поможем вам разобраться в том, как с помощью известной площади определить стороны простых фигур, таких как треугольник, прямоугольник и круг.
Определение сторон фигуры по площади может оказаться сложным для новичков. Если вы сталкивались с трудностями в подобных расчетах, то наш гайд будет очень полезен для вас. В этой статье мы рассмотрим несколько методов расчета, которые помогут вам быстро и точно найти значения сторон фигуры по известной площади.
Мы рекомендуем обратить внимание на примеры расчета, чтобы лучше понять, как выполнить расчет сторон фигуры по известной площади. Подобные расчеты важны не только в учебных целях, но и на практике – при проектировании домов, дизайне интерьера, разработке игр и многих других областях.
Расчет сторон по площади фигур
К слову, найти стороны по площади фигуры не такая уж и сложная задача! Сегодняшний гайд поможет вам быстро и правильно определить неизвестные стороны треугольника, квадрата, прямоугольника и круга.
Расчет сторон треугольника по заданной площади
Если известна площадь треугольника и одна из сторон, то оставшиеся стороны можно определить по формуле:
сторона_1 = 2 * площадь / сторона_2
сторона_3 = sqrt(сторона_2^2 — (4 * площадь^2) / сторона_2^2)
Расчет сторон квадрата и прямоугольника по заданной площади
Если известна площадь квадрата или прямоугольника, то стороны можно найти по следующим формулам:
- сторона_квадрата = sqrt(площадь)
- сторона_прямоугольника_1 = площадь / сторона_прямоугольника_2
- сторона_прямоугольника_2 = площадь / сторона_прямоугольника_1
Расчет радиуса круга по заданной площади
Если известна площадь круга, то радиус можно найти по формуле:
радиус = sqrt(площадь / pi)
Теперь вы знаете, как найти стороны по площади фигур различных форм и размеров. Так что не бойтесь экспериментировать и считать, ведь математика — это прекрасно!
Примеры простых фигур и способы их расчета
Квадрат
Квадрат — это фигура с четырьмя равными сторонами, значит, для расчета площади нужно умножить сторону на саму себя.
Формула: S=а²
Прямоугольник
Прямоугольник имеет две пары равных сторон, поэтому для расчета его площади нужно умножить длину на ширину.
Формула: S=а*b
Треугольник
Площадь треугольника можно расcчитать по формуле Герона или через высоту, проведенную к одной из сторон.
- Формула Герона: S=√(p*(p-a)*(p-b)*(p-c)), где p — полупериметр a, b, c — стороны
- Формула через высоту: S=0.5*a*h, где a — основание, h — высота, проведенная к этому основанию
Круг
Для расчета площади круга нужно умножить квадрат радиуса на число π
Формула: S=πr²
Трапеция
Площадь трапеции вычисляется по формуле, использующей среднюю линию и высоту.
Формула: S=0.5*(a+b)*h, где a и b — основания, h — высота
Как использовать формулы для расчета сложных фигур
Для расчета площади сложных фигур, необходимо использовать соответствующие формулы. Например, для расчета площади круга, используется формула S=πr², где S – площадь, π – число Пи, r – радиус круга. Для расчета площади треугольника, используется формула S=½ah, где a – длина основания, h – высота треугольника.
Если нужно посчитать площадь нестандартной фигуры, можно разбить ее на более простые части и посчитать их площадь отдельно. Например, для расчета площади трапеции, можно разбить ее на два треугольника и прямоугольник, а затем применить соответствующие формулы.
Помимо формул для расчета площади, существуют также формулы для расчета периметра и диаметра фигур. Знание данных формул поможет не только посчитать площадь, но и оценить длину границ фигуры и ее диаметр.
Важно помнить, что точность расчетов зависит от точности измерений сторон и углов фигуры. При неправильном измерении может получиться неверный результат при расчете площади.
- Пример
- Для расчета площади круга с радиусом 5 см, используем формулу S=πr². Решаем:
- π=3,14
- r=5
- S=3,14*5²=78,5 см²
Инструменты для быстрого и точного расчета площади
Для того чтобы быстро и точно рассчитать площадь фигуры, существует несколько инструментов:
- Калькулятор — позволяет быстро производить расчеты, сокращая время на примитивные операции.
- Геометрические фигуры — знание формул площади и периметра геометрических фигур позволяет быстро и точно расчитать площадь.
- Графический редактор — позволяет измерять площадь на изображении фигуры, возможность выделения определенных участков и расчета площади.
- Приборы точного замера расстояний — лазерный дальномер и металлический линейка позволяют с точностью до миллиметра провести замеры и рассчитать площадь.
Выбирайте инструмент, который подходит конкретно вам, учитывая характеристики фигуры и задачу, которую необходимо решить.
| Инструмент | Преимущества | Недостатки |
|---|---|---|
| Калькулятор | Быстрота расчетов | Не подходит для всех форм фигур |
| Геометрические фигуры | Высокая точность | Необходимо знание формул |
| Графический редактор | Возможность измерения на изображении | Требуется определенная программная поддержка |
| Приборы точного замера расстояний | Максимальная точность | Могут быть не удобны в использовании |
Учет нестандартных форм и неровностей в расчетах
При расчете площади фигур, основанных на нестандартных формах и неровностях, важно обратить внимание на каждый отдельный элемент. Например, при расчете площади комнаты с выступающей нишей необходимо учесть площадь и форму ниши и вычесть ее из общей площади.
О принципах расчета таких фигур нужно думать заранее, чтобы не допустить ошибок в расчетах и не потратить потом дополнительное время на их исправление.
Важно также обратить внимание на использование правильной единицы измерения. Например, при расчете площади комнаты, в которой высота потолков отличается в разных частях, необходимо использовать формулу площади треугольника, умноженную на высоту. В этом случае важно провести все расчеты в одинаковых единицах измерения.
- Для точности расчетов также необходимо учитывать неровности поверхности, на которой проводятся измерения. Например, в комнатах с неровными стенами или кривыми углами, нужно внести соответствующие корректировки в формулу расчета площади.
- Также можно использовать метод аппроксимации для определения площади нестандартных фигур. Данный метод позволяет приблизительно определить площадь, проводя замеры в нескольких ключевых точках фигуры и на основании полученных данных рассчитывать площадь.
Советы по сохранению точности в расчетах и избежанию ошибок
Используйте единицы измерения
Перед началом расчетов убедитесь, что вы используете правильные единицы измерения для каждого параметра. Например, если вы хотите вычислить площадь прямоугольника, то ширина и высота должны быть измерены в одной и той же единице, например, в сантиметрах.
Проверяйте формулы
Перед тем, как начать расчеты, проверьте формулы. Возможно, вы уже знакомы с формулой для расчета площади круга, но неверно взяли значение радиуса. Внимательно проверьте каждый параметр и каждую формулу, чтобы избежать ошибок в расчетах.
Проверяйте свои вычисления
После того, как вы закончили все расчеты, проверьте свои вычисления, чтобы убедиться в их точности. Можете использовать калькулятор или другие инструменты, чтобы перепроверить свои результаты.
Если возникли сомнения, перепроверьте
Если вы не уверены в своих вычислениях, не стесняйтесь их перепроверить. Лучше потратить немного больше времени на тщательные расчеты, чем допустить ошибку, которая может привести к неправильным результатам. Если вы не можете понять, почему ваш результат неправильный, обратитесь за помощью к другим людям или используйте специальные программы для расчетов.
Не округляйте результаты до последней цифры
Всегда оставляйте некоторую запасную цифру, чтобы избежать закономерных ошибок округления. Например, если ваш результат 5,54567, то лучше округлить до двух знаков после запятой до 5,55, а не до 5,54. Это может избежать дополнительных ошибок в будущем.
Применение расчетов площади фигур в повседневной жизни
Расчет площади различных фигур может пригодиться в повседневной жизни. Например, при выборе покрытия для пола или стен необходимо рассчитать площадь помещения и приобрести нужное количество материала.
Также расчеты площади могут пригодиться при планировании мебели в комнате. Необходимо знать площадь комнаты, чтобы определить, сколько мебели будет в ней умещаться.
Расчеты площади фигур могут также пригодиться при проектировании сада или зеленых насаждений. Необходимо знать площадь участка, чтобы определить, сколько растений, травы и деревьев необходимо приобрести.
В области строительства расчеты площади могут пригодиться при проектировании зданий, дорог и мостов. Используя информацию о площади, можно рассчитать необходимое количество строительных материалов.
Расчитывать площади фигур можно с помощью математических формул или с использованием онлайн-калькуляторов.
Где d – диагональ,b – сторона.
Где d – диагональ,α – угол между диагональю и искомой стороной.
Где d – диагональ,α – угол между диагональю и другой стороной.
Где S – площадь, b– известная сторона.
Где P – периметр, b – известная сторона.
Где d – диагональ, α – угол между диагоналями.
- Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
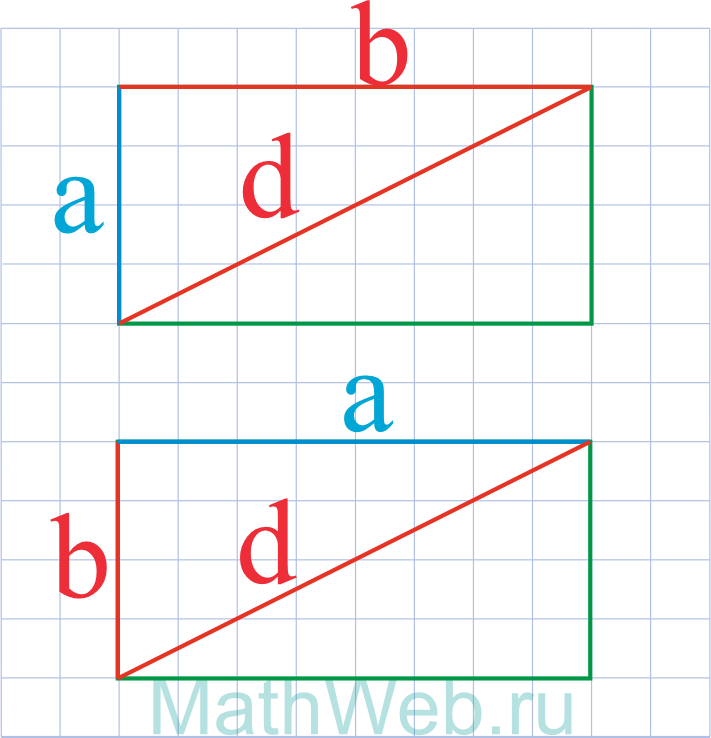 |
a = √d2 ― b2 |
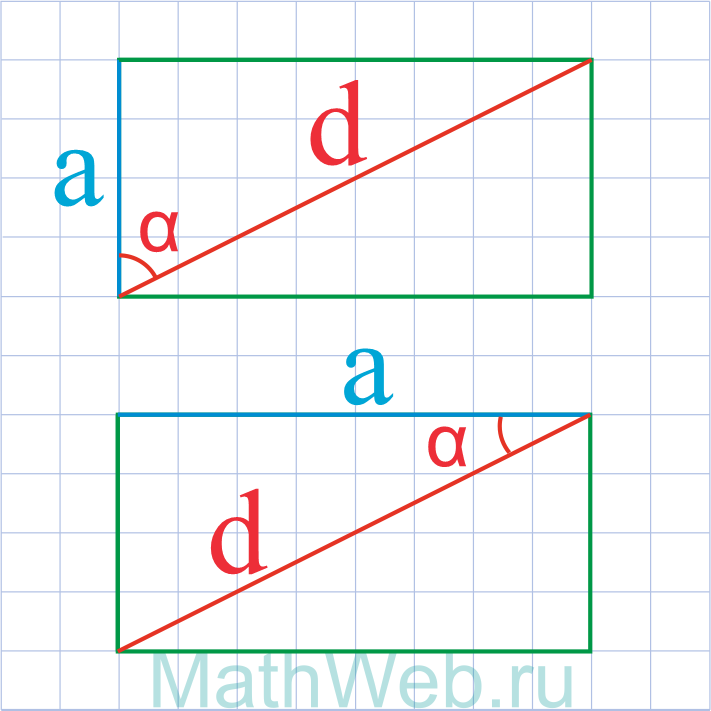 |
a = d·cos(α) |
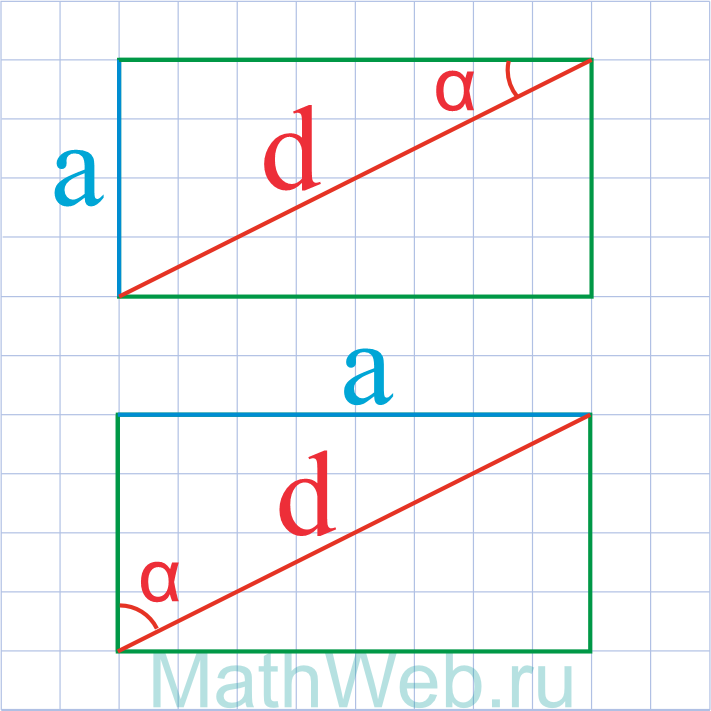 |
a = d·sin(α) |
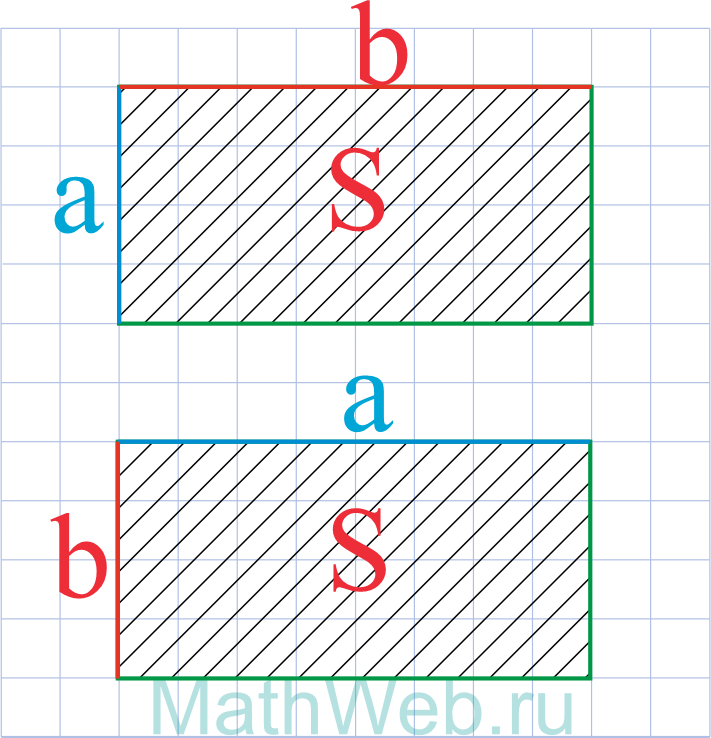 |
a = S b |
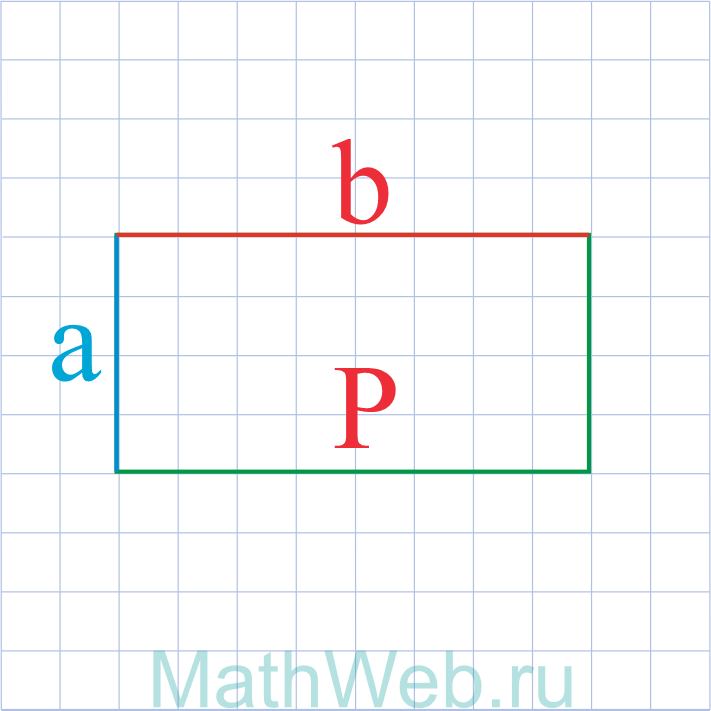 |
a = P – 2b 2 |
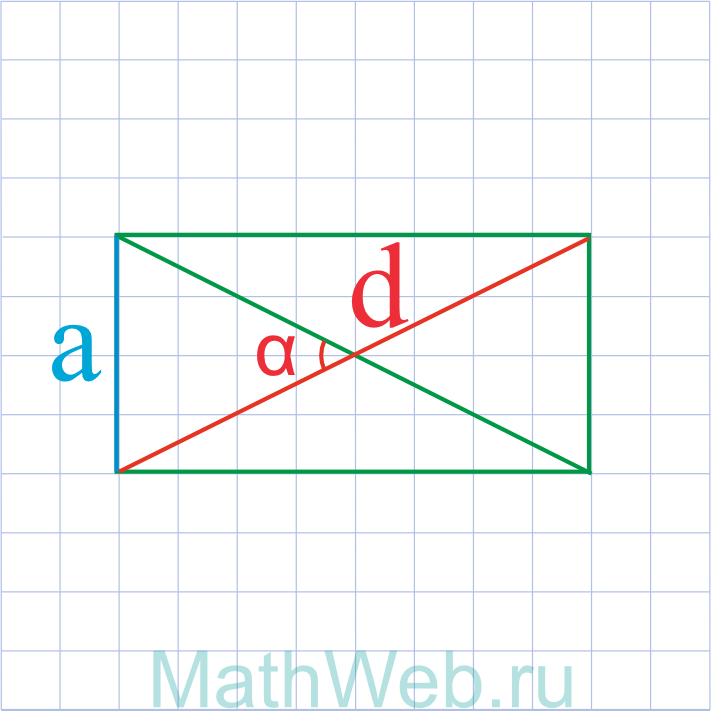 |
a = d·sin(0.5·α) |
Сторона прямоугольника по площади и другой стороне в м
Введите длину стороны a в м:
0.00м
S = a • b ⇒ b = S : a
S — площадь прямоугольника в м2 (квадратных метрах);
a — известная длина одной из сторон прямоугольника в м (метрах).
b — неизвестная длина другой стороны прямоугольника в м (метрах)
Например:
Площадь прямоугольника равна 192 м2, одна сторона равна 8 м. Найдите длину другой стороны прямоугольника.
Краткое решение: b = S : a = 192 : 8 = 24 м.
Площадь прямоугольника равна 144 м2, длина прямоугольника равна 18 м. Найдите его ширину.
Краткое решение: ширина прямоугольника b = S : a = 144 : 18 = 8 м.
Зная в прямоугольнике площадь и сторону можно найти вторую сторону, и затем все остальные параметры по порядку. Вторая сторона прямоугольника будет равна отношению площади к известной стороне.
b=S/a
Для того чтобы найти периметр прямоугольника через площадь и сторону, необходимо подставить в формулу вместо второй стороны полученное отношение
P=2(a+b)=2(a+S/a)
Диагональ прямоугольника можно найти через теорему Пифагора в прямоугольном треугольнике, который она образует. Обе диагонали прямоугольника принимают одно и то же значение. Выразив b через площадь и известную сторону, получим следующее выражение. (рис. 56.1)
d_1=d_2=√(a^2+b^2 )=√(a^2+(S/a)^2 )=√(a^2+S^2/a^2 )
Используя тригонометрические отношения в полученном треугольнике можно найти углы при пересечении диагоналей со сторонами. Для этого проще всего будет использовать тангенс, как отношение катетов друг к другу. Точно также, как и в предыдущих формулах, заменяем неизвестную сторону на равное ей выражение.
α=arc tan〖b/a〗=arc tan〖S/a^2 〗
β=arc tan〖a/b=arc tan〖a^2/S〗 〗
Угол, образованный при пересечении диагоналей, и дополнительный ему до 180° зависят только от углов при диагонали и стороне, и равны удвоенному их значению. (рис. 56.2)
γ=2α
δ=2β
Радиус описанной вокруг прямоугольника окружности равен половине диагонали, так как лежит на ней и исходит из точки пересечения диагоналей. (рис. 56.3)
R=d/2=√(a^2+S^2/a^2 )/2