как найти сторону прямоугольника, если известен периметр и другая сторона?
Профи
(698),
закрыт
13 лет назад
maxim wolf
Новичок
(0)
13 лет назад
вычитаешь из периметра удвоенное произведение известной стороны а затем получившийся результат делишь пополам…. вот и сторона прямоугольника
Екатерина ***
Знаток
(277)
13 лет назад
периметр прямоугольника равен 2(A+B)=>
допустим одна сторона будет 10, периметр будет 40 (так нагляднее объяснить) , а другую сторону мы обозначим за х, тогда
2(х+5)=40
2х+10=40
2х=30
х=15
ффффф ффффффф
Ученик
(102)
2 года назад
9000000000000000000000000000000000000000000000000000000000000000000+1111111111111111111111111111111111111111111111111111111111=112345678963214879076+1212313123123-124135236135326345321-123141123421/4444444444444444444444444444444444444444444444+9999999999999999999999999999999999999999999999999999999999999999999999999999=
сколько будет ???
Школьная математика » Блог » Как найти стороны прямоугольника при известных периметре и площади
В этой статье я хочу рассмотреть две математические задачи повышенной сложности для 4 класса.
Видеоурок по теме этой статьи можно посмотреть по ссылке.
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
С этими задачами, я уверен, без труда справится более старший школьник, знакомый с решением системы уравнений и квадратных уравнений. Кстати, подобная задача есть в учебнике по геометрии Атанасяна, глава VI № 454 пункт б за 8 класс.
Но почему же эти задачи указаны в математических сборниках как задачи для 4 класса, в котором еще не изучают алгебраические понятия и методы решения? Нет ли здесь ошибки?
Нет, никакой ошибки здесь нет. Эти, и аналогичные им задачи можно решить и без использования алгебраических знаний.
Первое, что приходит на ум – это по значению периметра прямоугольника (а периметр – это удвоенная сумма двух его сторон) найти сумму двух сторон, а после простым подбором определить два числа, произведение которых равно данной по условию площади прямоугольника, а сумма – половине периметра.
Я хочу показать вам математически точное решение, которое безо всяких подборов приводит к правильному результату.
Нахождение сторон прямоугольника при известных периметре и площади
Рассмотрим первую задачу:
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Как известно, периметр прямоугольника находится по формуле ({color{red} P=2cdot (a+b)}) , площадь – по формуле ({color{red} S=acdot b}) .
Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:
({color{red} a + b = 24 : 2 = 12}) см.
А дальше мы рассуждаем так.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной ({color{red} 12 : 2 = 6}) см.
Тогда площадь этого квадрата равна
({color{red}S_{k}=6cdot 6=36}) см2.
По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.
({color{red} S–S _{k}=36-32=4}) см2.
Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.
Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.
Но на какое?
Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.
Тогда, ширина искомого прямоугольника будет равна:
({color{red} a=6-2=4}) см
а длина:
({color{red} b=6+2=8}) см.
Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:
({color{red} P=2cdot (4+8)=2cdot 12=24}) см
({color{red} S=4cdot 8=32}) см2.
Задача решена верно.
Теперь рассмотрим вторую задачу.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
Находим полупериметр, то есть, сумму двух сторон прямоугольника.
({color{red} a+b=46:2=23}) см.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. ({color{red} 23=11+12}).
Площадь такого прямоугольника равна:
({color{red}S_{2}=11cdot 12=132}) см2.
Разница между полученной площадью и заданной по условию задачи составляет:
({color{red}S_{2}-S=132-126=6}) см2.
6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.
Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.
Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).
Находим ширину искомого прямоугольника:
({color{red} a=11-2=9}) см.
Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:
({color{red} b=12+2=14}) см.
Проведем проверку:
({color{red} P=2cdot (9+14)=2cdot 23=46}) см.
({color{red}S=9cdot 14=126}) см2.
И эта задача решена тоже верно.
На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.
Вам также пригодится:
Периметр любого прямоугольника составляет 2а+2с. То есть сумме удвоенных произведений противоположных сторон. Кроме того, по свойствам прямоугольника известно, что у него противоположные стороны попарно равны. То есть а=а, с=с. Отсюда имеем: 2а, 2с.
По условию задачи, 2а=1/5*400. то есть 2а=80.
Подставляем 2а в формулу периметра прямоугольника: 2а+2с. Получаем 80+2с=200. Отсюда находим с: с=(200-80):2. с=60. Вот мы нашли одну сторону прямоугольника (с).
Теперь находим сторону а. При этом снова используем формулу периметра прямоугольника, подставив туда найденное значение с. Получаем:
2а+2с=200
2а+120=200
2а=200-120
2а=80
а=40
Вот мы нашли вторую сторону (а).
Итак, стороны прямоугольника равны: а=40, с=60.
Проверка:
Находим периметр, имея заданные стороны (а и с)
Р=2а+2с. Подставляем известные нам а и с. Получаем:
Р=2*40+2*60
Р=80+120
Р=200
Итак, у нас периметр получился равным 200 см., что соответсвует условиям задачи. Значит, найденные значения а и с у нас правильные. а=40, с=60
Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла.
Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой.
Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами,
квадрат — это особенный случай прямоугольника.
- Сторона прямоугольника через диагональ и угол между
диагональю и стороной - Сторона прямоугольника через диагональ и известную
сторону - Сторона прямоугольника через площадь и другую известную
сторону - Сторона прямоугольника через периметр и другую известную
сторону - Сторона прямоугольника через диагональ и угол между
диагоналями
Через диагональ и угол между диагональю и стороной
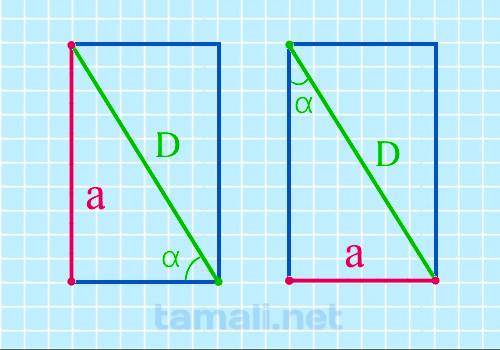
Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол
средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно
воспользоваться следующей формулой:
a = d * sinα
где d — это диагональ, а, b — одна из сторон фигуры.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой
стороной — 60º.
Решение.
D = 16, β = 60º, b = ?
b = 16 cos 60º
b = 16 * 0.5 = 8 см.
Через его площадь и известную сторону
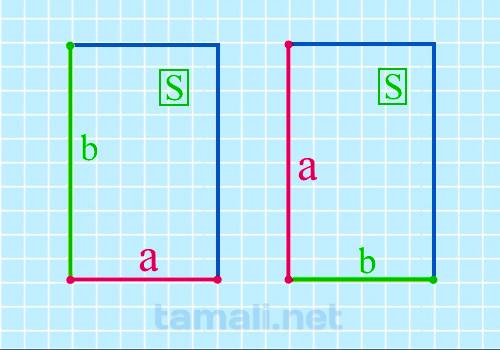
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно
a = S / b
где S — площадь прямоугольника, b — известная сторона.
Цифр после
запятой:
Результат в:
Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем
известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.
Через диагональ и известную сторону
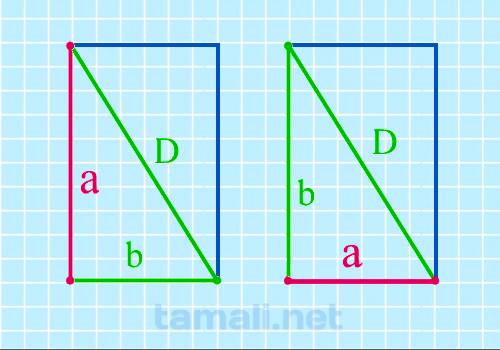
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.
Диагональ
— это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них
разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а
две соседние стороны — остальные стороны треугольника. Отсюда :
a = √(d² — b²)
где d — диагональ, а, b — стороны.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.
Решение.
D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см.
Через диагональ и угол между диагоналями
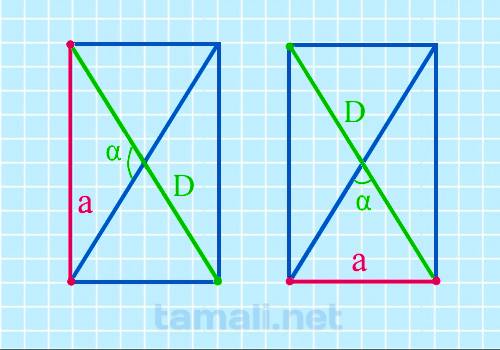
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать
сторону прямоугольника, зная следующую формулу:
a = D • sin(α/2)
где D — диагональ, α — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти
сторону.
Решение.
a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.
Через периметр и другую известную сторону
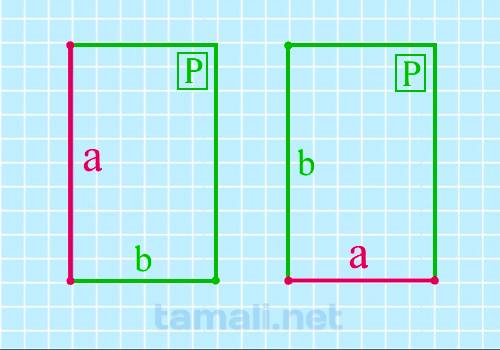
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра
для получения длины. P = 2 (a + b).
a = (P — 2b) / 2
где P — периметр прямоугольника, b — другая известная сторона.
Цифр после
запятой:
Результат в:
Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4).Вычислив,
получим 12 см.
Другие примеры по решению задач на прямоугольник с использованием длины и ширины
- Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
Результат: P
прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов - Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3
м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы
преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см.
Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см². - Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти
периметр прямоугольника. Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17,
используем теорему Пифагора и составим уравнение: AB² +AD² =BD².
Получаем: х² +(х+7)² =17² ⇒ х² +х² +14х+49=289; 2х² +14х-240=0; х² +7х-120=0,
отсюда по теореме Виета х1 =-15; х2 =8.Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника: P = 2∙ (AB+AD); P = 2∙ (8+15); P = 46 см.
Ответ: 46 см.
Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены
ниже.
- Прямоугольник — это четырехугольник.
- Противоположные стороны прямоугольника являются равными и параллельны друг другу.
- Внутренний угол прямоугольника при каждой вершине равен 90°.
- Сумма внутренних углов равна 360°.
- Диагонали пересекаются друг с другом.
- Длина диагоналей равна.
- Длина диагоналей может быть получена с помощью теоремы Пифагора. Длина диагонали со сторонами a
и b равна, диагональ = ( a2 + b2). - Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
- Все прямоугольники являются параллелограммами, но все параллелограммы не являются
прямоугольниками.
Математика
Компоненты арифметических действий и их взаимосвязь.
- Компоненты при сложении:
1слагаемое, 2слагаемое, сумма.
- Компоненты при вычитании:
уменьшаемое, вычитаемое, разность.
- Компоненты при умножении:
1 множитель, 2множитель, произведение.
- Компоненты при делении:
делимое, делитель ,частное.
- Назвать результаты всех действий:
при сложении – сумма
при вычитании – разность
при умножении – произведение
при делении – частное
- Как найти неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Х+4=12 или 4+х=12
Х=12-4 х=12-4
Х=8 х=8
8+4=12 4+8=12
12=12 12=12
- Как найти неизвестное уменьшаемое?
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Х-7=3
Х=3+7
Х=10
10-7=3
3=3
- Как найти неизвестное вычитаемое?
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
8-х =5
х=8-5
х=3
8-3=5
5=5
9 Как найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х·3=6 4·х=8
х=6:3 х=8:4
х=2 х=2
2·3=6 4·2=8
6=6 8=8
10 Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
х:5=3
х=3·5
х=15
15:5=3
3=3
- Как найти неизвестный делитель?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
6:х=2
х =6:2
х=3
6:3=2
2=2
Геометрический материал.
- Что такое квадрат?
Квадрат – это прямоугольник, у которого все стороны равны.
- Что такое прямоугольник?
Прямоугольник – это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника равны.
- Что такое треугольник?
Треугольник – многоугольник, у которого три угла и три стороны.
15 Что такое четырёхугольник?
Четырёхугольник – геометрическая фигура, у которой четыре угла и четыре стороны.
- Что такое периметр?
Периметр( Ρ) – это сумма длин сторон какой-нибудь геометрической фигуры.
- Что такое площадь?
Площадь(S) – это внутренняя часть какой-нибудь геометрической фигуры
(прямоугольника, квадрата и т.д)
- Как найти периметр квадрата?
У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ□ разделить на 4.
a□ = Ρ□ : 4
- Как найти периметр прямоугольника?
Чтобы найти периметр прямоугольника, нужно сложить все 4 стороны прямоугольника
Или
сложить длину и ширину прямоугольника и умножить на 2.
Ρ▬=a+b+a+b
или
Ρ▬=(a+b)·2
- Как найти периметр треугольника?
Чтобы найти периметр треугольника, нужно сложить все 3 стороны.
- Как найти сторону квадрата, если известен периметр?
У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.
a=Ρ:4
- Как найти сторону прямоугольника, если известен периметр и другая сторона?
Чтобы найти сторону прямоугольника, нужно Ρ▬разделить на 2 и вычесть другую сторону.
a▬=Ρ▬:2 – b
b▬=Ρ▬:2 – a
22 В каких единицах измеряется периметр?
Периметр измеряется в мм, см, дм, метрах.
23 Как найти площадь квадрата?
Площадь квадрата равна произведению двух его сторон.
S□ = a · a
24 Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, надо длину прямоугольника умножить на его ширину.
S█ = a · b
25 Как найти сторону прямоугольника, если известна площадь и другая его сторона?
Чтобы найти одну из сторон прямоугольника, нужно площадь прямоугольника разделить на известную сторону.
a▬=S▬ : b
b▬= S ▬ : a
26 В каких единицах измеряется площадь?
Площадь измеряется в квадратных единицах: мм², см², дм², м².
27 Назвать единицы длины.
Единицы длины – мм, см, дм, м, км.
28 Рассказать таблицу мер длины.
1см = 10мм
1дм = 10см
1дм = 100мм
1м = 10 дм
1м = 100 см
1км = 1000м
29 Сколько квадратных сантиметров
в 1квадратном метре?
1м² = 10 000см²
30 Сколько квадратных дециметров
в 1 квадратном метре?
1м² = 100дм²
31 Рассказать таблицу мер площади.
1м² = 100дм² = 10 000см²
1дм² = 100см² = 10 000мм²
1см² = 100мм²
Масса.
32 Назвать единицы массы.
Масса измеряется в граммах, килограммах, центнерах, тоннах.
33 Рассказать таблицу мер массы.
1кг = 1000г
1ц = 100кг
1т = 10ц
1т = 1000кг
Время.
34 Назвать единицы измерения времени.
Время измеряется секундами, минутами, часами, сутками, неделями, месяцами, годами, веками.
35 Рассказать таблицу мер времени.
1мин = 60сек.
1час = 60мин
1час = 3600сек.
1сут. = 24часа
1год = 12мес. = 365сут. или 366сут.
1век = 100лет
Взаимосвязь скорости, времени и расстояния.
36 Как найти скорость?
Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.
v = S : t
37 Как найти время?
Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость ( v ).
t = S : v
38 Как найти расстояние?
Чтобы найти расстояние ( S ), нужно скорость ( v ) умножить на время ( t ).
S = v · t
Взаимосвязь цены, количества, стоимости.
39 Что такое цена?
Цена – стоимость одного предмета, единицы товара.
40 Как найти стоимость?
Чтобы найти стоимость, нужно цену умножить на количество.
Ст = Ц · К
41 Как найти цену?
Чтобы найти цену, нужно стоимость разделить на количество.
Ц = Ст : К
42 Как найти количество?
Чтобы найти количество, нужно стоимость разделить на цену.
К = Ст : Ц
Задачи на дроби.
43
Дробь – ⅔
2 – числитель
3 – знаменатель
44 Как найти дробь числа?
Чтобы найти дробь числа, нужно число разделить на знаменатель, а потом умножить на числитель.
45 Как найти число по дроби?
Чтобы найти число по дроби, нужно число разделить на числитель и умножить на знаменатель.
Взаимосвязь работы, времени и производительности.
46 Что такое производительность?
Как найти производительность?
Производительностью ( v ) называют работу, выполненную за единицу времени.
Чтобы найти производительность ( v ), надо всю выполненную работу разделить на время.
v = A : t
47 Как найти выполненную работу?
Выполненная работа равна производительности, умноженной на время работы.
A = v · t
48 Как найти время работы?
Чтобы узнать время работы, надо работу разделить на производительность.
t = A : v
49 Как найти среднее арифметическое?
Чтобы найти среднее арифметическое надо сумму разделить на число слагаемых.
