Общая характеристика
В мире имеется множество предметов с формой параллелепипеда. Люди обычно не задумываются об этом, но архитектура и различные массивные строения состоят из нескольких граней. Выглядеть параллелепипед может по-разному в зависимости от типа.
Основные понятия и классификация
Определение параллелепипеда, пирамиды, куба и других многогранников было известно с древнейших времен. Основными характеристиками являются простота и значимость.
Выведенные формулы V и S значимы для решения различных задач с практическим содержанием и доказательства теорем (по чертежам). Виды параллелепипеда:
- Прямой. Четыре боковые грани имеют углы по 90 градусов.
- Прямоугольный. Каждая сторона фигуры является прямоугольной.
- Наклонный.
- Двугранный, трехгранный. Состоит из нескольких граней под углом 90 градусов.
- Наклонный, диагональный. Боковые грани не перпендикулярны основаниям.
- Ромбоэдр. Стороны являются одинаковыми ромбами.
- Куб. Параллелепипед с равными (квадратными) сторонами.
В 6 классе на уроке геометрии изучают планиметрию (плоские фигуры). Здесь представлена развертка плоскостей.
Две стороны параллелепипеда, не имеющие общего ребра, называются противоположными, а содержащие единую линию — смежными. С точки зрения плоскостей, расположенных параллельно, внутри пересекаются три их пары. Эти вершины соединяет отрезок — диагональ. Длина трех ребер правильного многогранника называется измерением. Главным условием является общая вершина.
При решении задач важно понятие высоты — перпендикуляра, опущенного из любой вершины на обратную сторону. Грань, на которую опускается высота, считается основанием. Свойства параллелепипеда:
- любые стороны являются параллелограммами (с симметрией);
- стороны, расположенные друг против друга, будут параллельными и равными.
Кирпич — отличный пример прямоугольного параллелепипеда (ПП). Также его форму имеют девятиэтажные панельные дома, шифоньеры, шкафы-купе, контейнеры для хранения продуктов и прочие предметы быта.
Диагонали поверхности пересекаются и этой центральной точкой делятся на несколько частей. Они равны d2=a2+b2+c2
Грани параллелепипеда спереди и сзади равнозначны, также как верхняя и нижняя стороны, но не равны, поскольку не противоположные, а смежные.
Формулы и анализ
Для ПП верно мнение, что его объем равен величине тройного произведения векторов трех сторон, исходящих из единой вершины. Формулы для ПП:
- V=a*b*c.
- S б =2*c*(a+b).
- S п =2*(a*b+b*c+a*c).
Расшифровка обозначений: V — объем фигуры, S — площадь поверхности, a — длина, b — ширина, c — высота.
Особым случаем параллелепипеда, в котором все стороны квадраты, является куб. Если любую из сторон обозначить буквой a, то для поверхности и объема используются формулы: S=6*a*2, V=3*а. В них V — объем фигуры, a — длина грани.
Последняя разновидность параллелепипеда — прямой тип. Его основанием будет параллелограмм, а основанием ПП — прямоугольник. Формулы, используемые в математике и геометрии: Sб=Ро*h, Sп=Sб+2Sо, V=Sо*h.
Для нахождения ответов недостаточно знать только свойства геометрической фигуры. Могут пригодиться формулы для вычисления S и V.
Диагональ ПП равна сложению квадратов его измерений: d2 = a2 + b2 + c2. Эта формула получается из теоремы Пифагора.
∆BAD — прямоугольный, поэтому BD2 = AB2 + AD2 = b2 + c2.
∆BDD1 является прямоугольным, значит, BD12 = BD2 + DD12. Нужно подставить значение: d2 = a2 + b2 + c2.
Стандартная формула: V= Sосн*h. Расшифровка обозначений: V — объем параллелепипеда, Sосн — площадь основания, h — высота.
S находится так же, как показатель параллелограмма или прямоугольника. При решении тестов и экзаменационных задач легче вычислять показатели призмы, в основе которой находится прямой угол. Также может пригодиться формула расчета стороны параллелепипеда Sбок = P*h, где:
- Sбок — площадь параллелепипеда;
- Р — периметр;
- h — высота, перпендикулярная основанию.
Объем фигуры равен величине смешанного произведения нескольких векторов, выпущенных из единой точки.
Практическое применение
Для вычисления объема, высоты и прочих характеристик фигуры нужно знать теоретические основы и формулы. Решение задач входит в программу сдачи ЕГЭ и билеты при поступлении в вуз.
Доказательство теорем
Теоретически S боковой поверхности ПП равна S б. п. = 2 (a+b)c. S полной поверхности равна Sполн. поверхности ПП=2 (ab+ac+bc).
Объем ПП равен произведению трех его боковых частей, выходящих из единой вершины (три измерения ПП): abc.
Доказательство: так как у ПП боковые ребра перпендикулярны основанию, то они являются и его высотами — h=AA1=c. Если в основании лежит прямоугольник, то Sосн=AB ⋅ AD=ab. Диагональ d ПП можно найти по формуле d2=a2+b2+c2, где a, b, c — измерения ПП.
Если в основании расположен прямоугольник, то △ ABD прямоугольный, значит, по теореме Пифагора BD2=AB2+AD2=a2+b2. Если все боковые грани перпендикулярны основной линии, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD.
Когда △ BB1D прямоугольный, то по теореме Пифагора B1D=BB12+BD2.
Решение задач
Задача 1: известны ПП: 3, 4, 12 см, необходимо найти длину главной диагонали фигуры.
Поиск ответа на вопрос начинается с выстраивания схематического изображения, на котором означаются величины. Используется формула B1D2 = AB2 + AD2 + AA12. После вычислений получается выражение b2=169, b=13.
Задача 2: ребра ПП, выходящие из общей точки, равны 3 и 4, общая S — 94. Нужно найти третье ребро, выходящее из той же вершины.
Ребра обозначаются а1 и а2, а неизвестное — а3. Площадь поверхности выражается S = 2 (a1a2 + a1a3 + a2a3).
Далее получаем a3 (a1 + a2) = S/2 — a1a2. Неизвестное ребро: a3 = S/2 — a1a2/a1 + a2 = 47−12/7 = 5.
Задача 3: два ребра прямоугольного параллелепипеда, выходящие из общей точки, составляют 72 и 18, диагональ равна 78. Нужно определить объем фигуры.
Для решения требуется найти диагональ по формуле вычисления квадратного корня из суммы (a2 + b2 + c2), где a, b, c — ребра фигуры. 78 — корень из суммы 722 + 182 + c2. Решение:
- 78 = корень из суммы 5508+с2
- 782 = 5508 + с2
- с2 = 6084 — 5508.
- С2 = 576.
Ответ: объем составляет 576.
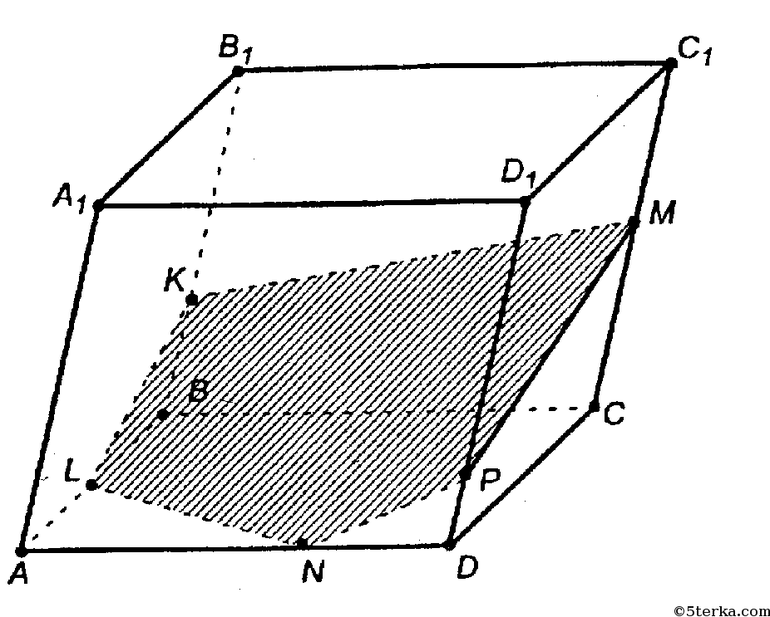
Задача 4: ребро наклонного параллелепипеда составляет 10 см, прямоугольник KLNM с измерениями 5 и 7 см является сечением фигуры, параллельным ребру. Нужно определить площадь боковой поверхности призмы.
KL и AD не являются равными, как пара ML и DC. Боковая S фигуры эквивалентна S сечения, умноженной на AA1, так как ребро перпендикулярно сечению. Ответ: 240 см².
Задача 5: ABCDA1B1C1D1 = 3, 4 см, боковое ребро — 12 см. Нужно определить диагональ ПП.
В основании лежит прямоугольник со сторонами АВ 3 см и AD 4 см. Боковое ребро составляет 3 см. BB1 является высотой ПП и равняется 12 см. Диагональ B1D2 = AB2 + BB1 2 += 9+16+144 = 169. B1D= 13 см.
Задача 6: основанием ПП служит квадрат, одна из вершин его верхнего основания одинаково удалена от всех вершин нижней части. Нужно найти высоту фигуры, если диагональ основания равна 8 см, а боковое ребро — 5 см.
Одна из вершин основания (F) равнозначно удалена от всех вершин нижнего основания параллелепипеда. Вместе с диагональю нижней части (AC) она образует равнобедренный ∆AFC. AF = AC по условию. AF является ребром фигуры.
В равнобедренном ∆AFC стороны одинаковы: AF=FC=5 см, AC=8 см. Высота ∆AFC будет являться высотой параллелепипеда.
Высота треугольника делит его основание пополам. По теореме Пифагора она равна:
- FK2 + (AC/2)2 = FC2;
- FK2 + 16 = 25;
- FK2 =25−16 = 9;
- FK = 3 см.
Высота фигуры составляет 3 см.
Установленные теоремы, доказательства, а также выведенные формулы помогают вычислить различные значения для фигуры.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 мая 2022 года; проверки требуют 4 правки.
Параллелепи́пед (др.-греч. παραλληλ-επίπεδον[1] от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — четырёхугольная призма, все грани которой являются параллелограммами.
Типы параллелепипеда[править | править код]
Прямоугольный параллелепипед
Различается несколько типов параллелепипедов:
- Наклонный — боковые грани не перпендикулярны основанию.
- Прямой — боковые грани перпендикулярны основанию.
- Прямоугольный — все грани являются прямоугольниками.
- Ромбоэдр — все грани являются равными ромбами.
- Куб — все грани являются квадратами.
Основные элементы[править | править код]
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
Свойства[править | править код]
- Параллелепипед симметричен относительно середины его диагонали.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Противолежащие грани параллелепипеда параллельны и равны.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Основные формулы[править | править код]
Прямой параллелепипед[править | править код]
Площадь боковой поверхности
Sб=Ро*h, где Ро — периметр основания, h — высота
Площадь полной поверхности
Sп=Sб+2Sо, где Sо — площадь основания
Объём
V=Sо*h
Прямоугольный параллелепипед[править | править код]
Площадь боковой поверхности
Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
Площадь полной поверхности
Sп=2(ab+bc+ac)
Объём
V=abc, где a, b, c — измерения прямоугольного параллелепипеда.
Куб[править | править код]
Площадь поверхности:
Объём: 

Произвольный параллелепипед[править | править код]
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения[2]:215.
В математическом анализе[править | править код]
В математическом анализе под n-мерным прямоугольным параллелепипедом 


Сечение параллелепипеда плоскостью[править | править код]
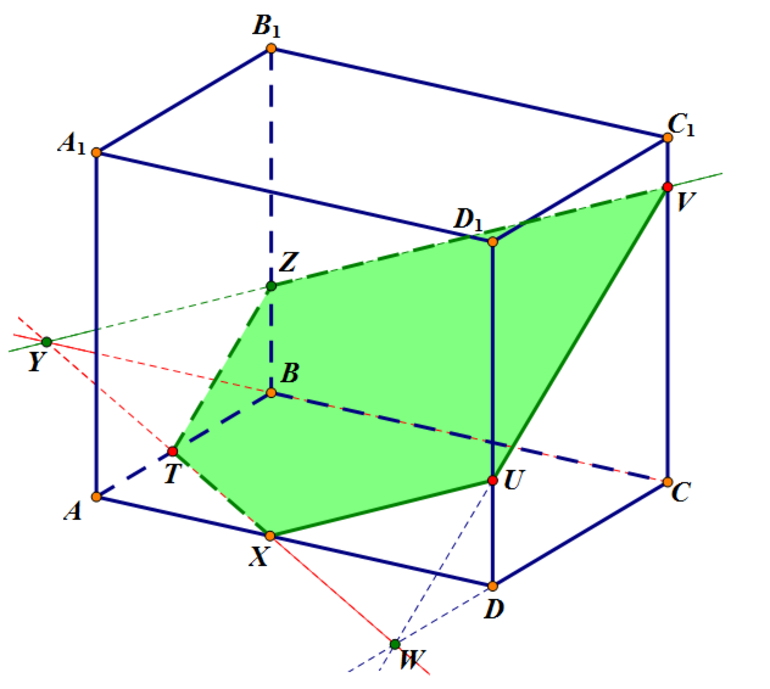
В зависимости от расположения секущей плоскости и параллелепипеда сечение параллелепипеда может быть треугольником, четырехугольником, пятиугольником и шестиугольником.
Примечания[править | править код]
- ↑ Древнегреческо-русский словарь Дворецкого «παραλληλεπίπεδον»
- ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
Ссылки[править | править код]
- Прямоугольный параллелепипед Архивная копия от 21 февраля 2020 на Wayback Machine
Математика
Тема 4: Площади и объемы
Урок 2: Прямоугольный параллелепипед
- Видео
- Тренажер
- Теория
Заметили ошибку?
Прямоугольный параллелепипед
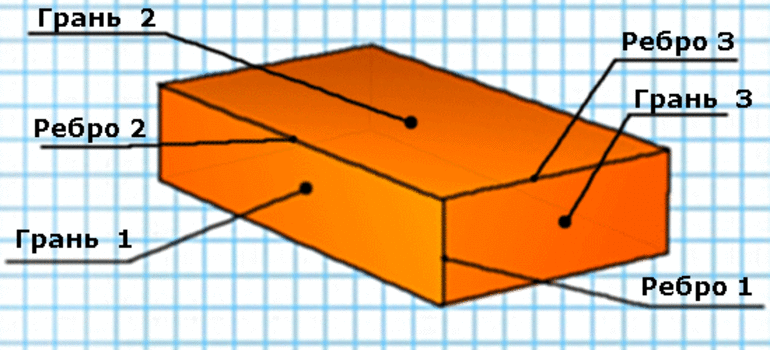
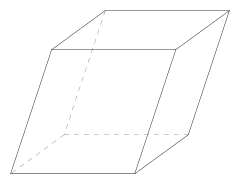
Мы часто встречаем предметы, имеющие похожую форму. Они могут быть сделаны из разного материала и окрашены в разные цвета. Например, коробок, шкаф, колонки, кирпич – похожи, но отличаются мелкими деталями: у колонок есть кнопки, у шкафа – двери. Все они напоминают по форме изображенный на рисунке предмет, не имеющий никаких второстепенных деталей. Это тело называется прямоугольный параллелепипед.
Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников, каждый из которых называют гранью прямоугольного параллелепипеда. Противоположные грани прямоугольного параллелепипеда равны.
Стороны прямоугольников, которые являются гранями прямоугольного параллелепипеда, называются ребрами этого прямоугольного параллелепипеда, а вершины граней – вершины параллелепипеда.
У прямоугольного параллелепипеда 6 граней, 12 ребер и 8 вершин. Прямоугольный параллелепипед имеет три измерения – длину, ширину и высоту.
Куб – это прямоугольный параллелепипед, у которого все измерения одинаковы. Поэтому поверхность куба состоит из 6 равных квадратов.
Названия всех ребер параллелепипеда: АВ, ВС, CD, DA, А1В1, В1С1, C1D1, D1A1, АА1, DD1, СС1, ВВ1.
Вершины параллелепипеда: А, В, С, D, А1, В1, С1, D1.
У параллелепипеда 6 граней, каждая грань повторяется 2 раза. Тогда можно записать формулу для площади поверхности прямоугольного параллелепипеда:
где a, b, c – длина, ширина и высота.
У прямоугольного параллелепипеда 12 ребер, причём длина a=DA=BC= D1A1= В1С1, ширина b=AB=CD=А1В1=C1D1, высота c=АА1=DD1=СС1=ВВ1. Тогда периметр (сумма всех сторон) прямоугольного параллелепипеда будет равен:
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.
Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).
Рисунок 1
Определение
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.
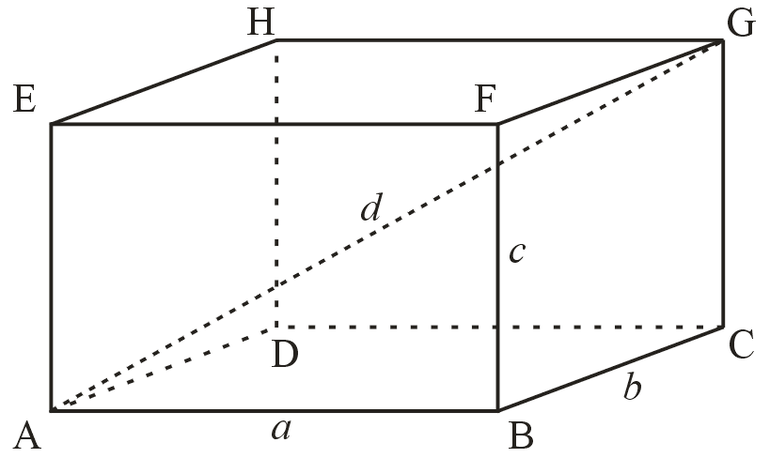
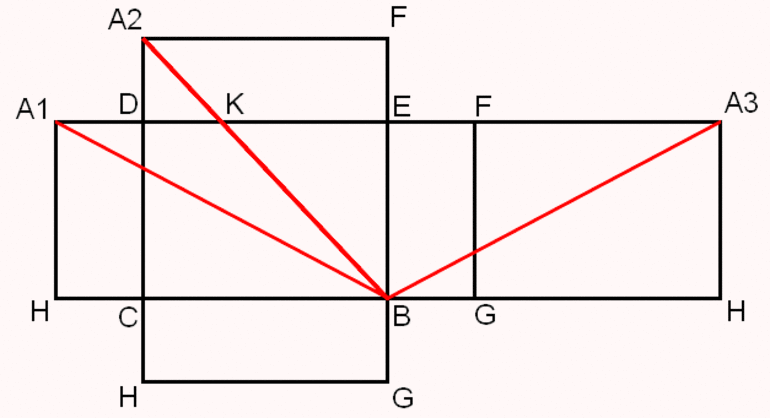
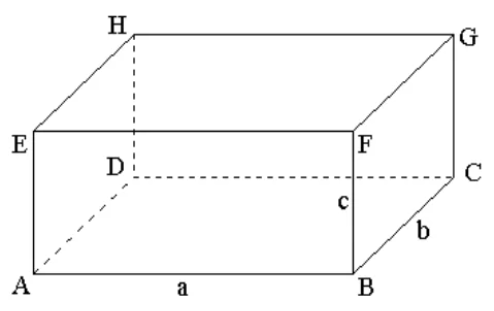
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.
У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
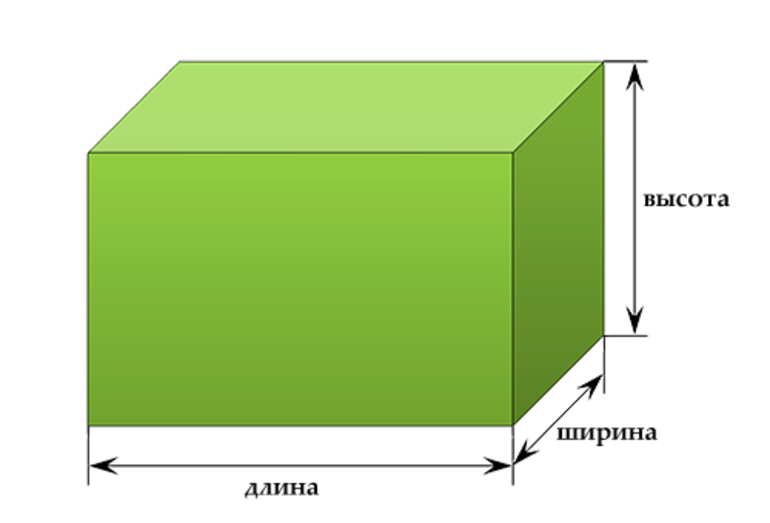
Длина, ширина, высота
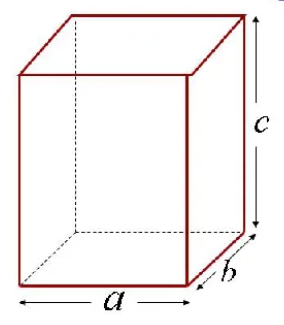
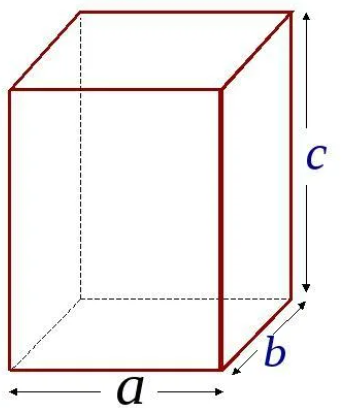
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.
Рисунок 3
Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.
Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.
Куб
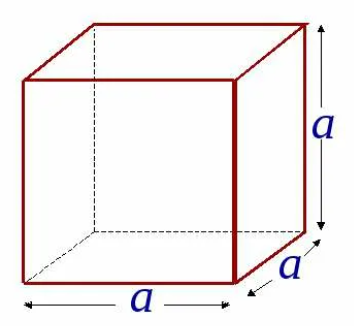
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).
Рисунок 4
Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2
Объем прямоугольного параллелепипеда
Рисунок 5
С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.
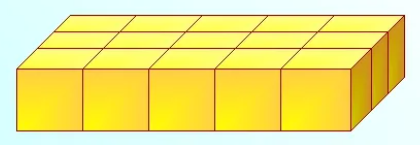
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.
Рисунок 6
За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.
Формула объема прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.
Рисунок 7
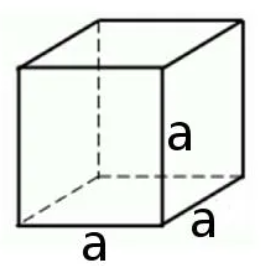
Объем куба
Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:
V=a3
Рисунок 8
Пирамида
Рисунок 9
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).
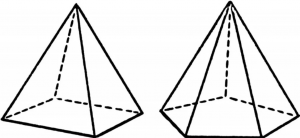
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).
Рисунок 10
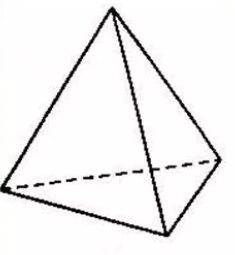
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.
Рисунок 11
Даниил Романович | Просмотров: 997
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
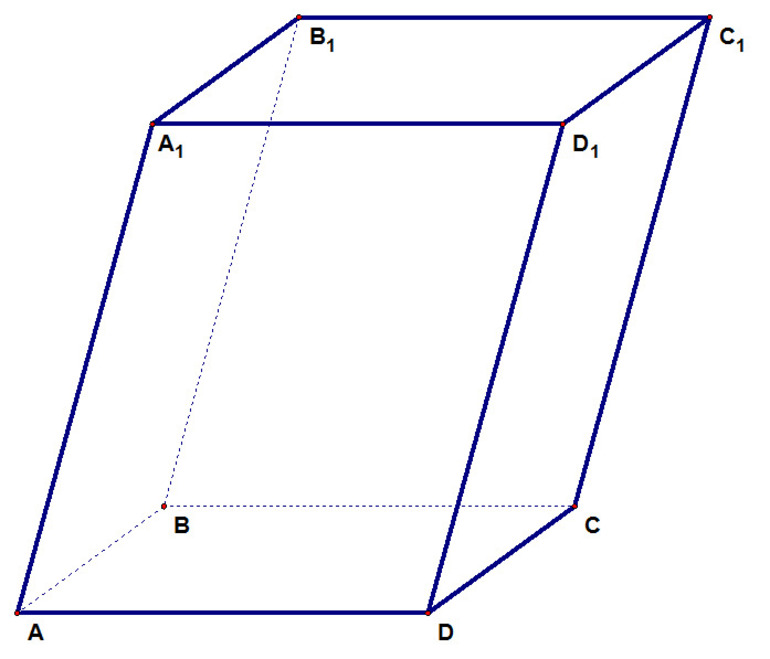
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ – длина;
$b$ – ширина;
$с$ – высота(она же боковое ребро);
$P_{осн}$ – периметр основания;
$S_{осн}$ – площадь основания;
$S_{бок}$ – площадь боковой поверхности;
$S_{п.п}$ – площадь полной поверхности;
$V$ – объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ – длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ – высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ – это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ – радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ – радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ – катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ – длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции. - Квадрат.
$S=a^2$, где $а$ – сторона квадрата.
Пример:
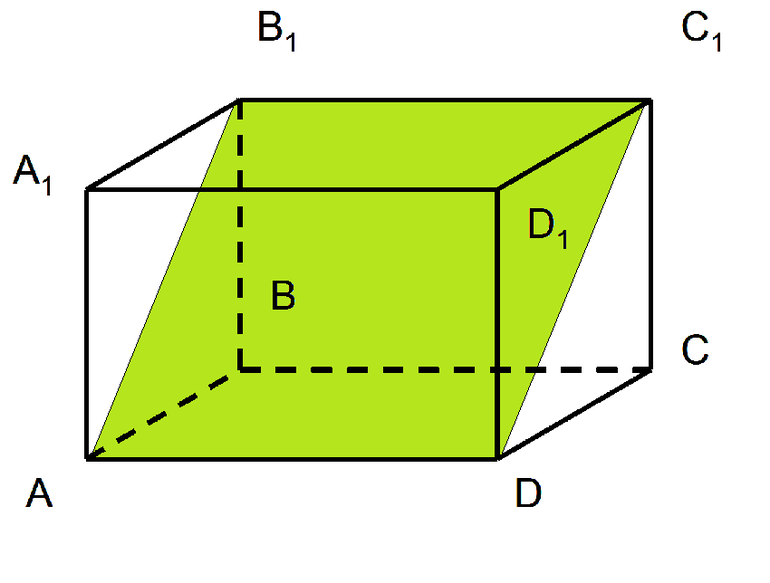
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ – стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$