Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.
Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.
Задача
Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.
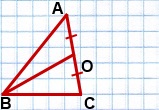
Дано: ∆ ABC,
AB=8 см,
BC=6 см,
BO — медиана, BO=√46 см.
Найти: AC.
Решение:
1) На луче BO отложим отрезок OD,
OD=BO.
2) Соединим точку D с точками A и C.
3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).
Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).
4) По свойству диагоналей параллелограмма,
![[A{C^2} + B{D^2} = 2(A{B^2} + B{C^2})]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-8d4dc767c7d582d5ef6c1e2a39ab93ac_l3.png "Rendered by QuickLaTeX.com")
![[BD = 2BO = 2sqrt {46} cm]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-91b14afa88efc1d2e42da6019fb027dd_l3.png "Rendered by QuickLaTeX.com")
![[A{C^2} + {(2sqrt {46} )^2} = 2({8^2} + {6^2})]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-f62db6abfe80052d5867b1d4ac685fe4_l3.png "Rendered by QuickLaTeX.com")
![[A{C^2} + 184 = 200]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-24e532a14688ec0def9f14048a2279da_l3.png "Rendered by QuickLaTeX.com")
![[A{C^2} = 16]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-0189c4b9dedf1683579c02084a47f825_l3.png "Rendered by QuickLaTeX.com")
![[AC = 4cm]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-70070a2f4a6932f84f60ee93fca8cfb0_l3.png "Rendered by QuickLaTeX.com")
Ответ: 4 см.
Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:
![[{(2{m_b})^2} + {b^2} = 2({a^2} + {c^2})]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-4f3dfc49d4721b00eac99f6f0dd8dcaf_l3.png "Rendered by QuickLaTeX.com")
![[4m_b^2 = 2({a^2} + {c^2}) - {b^2}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-8e7c95bee2d95072a992584f9251dff4_l3.png "Rendered by QuickLaTeX.com")
![[m_b^2 = frac{{2{a^2} + 2{c^2} - {b^2}}}{4}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-a155880dd53cce964c7927c397bf4e89_l3.png "Rendered by QuickLaTeX.com")
![[{{m_b} = frac{{sqrt {2{a^2} + 2{c^2} - {b^2}} }}{2}}]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-47ac765d8a41269f1ffd2cb165a7c1fc_l3.png "Rendered by QuickLaTeX.com")
Узнать ещё
Знание — сила. Познавательная информация
По сторонам и медиане найти сторону треугольника
Чтобы по сторонам и медиане найти сторону треугольника, достаточно знать ход решения задачи. Учить дополнительную формулу не обязательно.
По двум сторонам и медиане найти третью сторону треугольника — задача, обратная нахождению медианы треугольника по трем его сторонам .
Сначала рассмотрим, как по сторонам и медиане найти сторону треугольника, в общем виде.
Пусть в треугольнике ABC известны стороны AB=c, AC=b и медиана BF=m.
На луче BF отложим отрезок FD, FD=BF и соединим точку D с точками A и C.
Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD — параллелограмм (по признаку). А значит, мы можем применить свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Имеем: AC²+BD²=2(AB²+BC²). Отсюда b²+(2m)²=2(c²+BC²), b²+4m²=2c²+2BC², BC²=(b²+4m²-2c²)/2.
Переходим к решению конкретной задачи.
По двум сторонам 6 см и 8 см и медиане,проведенной к третьей стороне, найти неизвестную сторону треугольника. Длина медианы равна √46 см.
Пусть AB=6 см, BC=8 см, BF=√46 см. Рассуждая аналогично, получаем: AC²+BD²=2(AB²+BC²), AC²+(2√46)²=2(6²+8²), AC²+4∙46=200, AC²=200-184=16, AC=4 см.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Найти сторону треугольника через медиану и стороны
Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.
Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.
Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.
BO — медиана, BO=√46 см.
1) На луче BO отложим отрезок OD,
2) Соединим точку D с точками A и C.
3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).
Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).
Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:
[spoiler title=”источники:”]
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
Отличный повод вывести полезную (но очень редко) формулу и может даже две.
Речь пойдет опять о метрическом соотношении сторон в треугольнике (9-й класс), а именно связь между сторонами и медианами и в качестве бонуса выведем формулу нахождения стороны по двум другим и медиане, а ещё — формулу нахождения медианы по трём сторонам.
Условие
В треугольнике две стороны равны 11 и 23, а медиана, проведенная к третьей, равна 10. Найдите третью сторону.
Подсказка
Как и в последних нескольких задачах, подсказка будет — теорема косинусов. А именно — уравнение или даже система уравнений на теореме косинусов. Нужно только заметить смежные углы, косинусы которых – противоположны.
Формула №1
Нахождение стороны по двум известным и медиане
Выведется самостоятельно, если до самого конца использовать буквенные обозначения сторон и медианы.
Формула №2
Нахождение медианы по трём сторонам
Выводится из предыдущей формулы небольшими преобразованиями.
#школьное образование #школьная программа #образование
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c – стороны произвольного треугольника
α, β, γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.
H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b – катеты прямоугольного треугольника
с – гипотенуза
α – угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L – биссектриса, отрезок ME , исходящий из острого угла
a, b – катеты прямоугольного треугольника
с – гипотенуза
α, β – углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L – высота = биссектриса = медиана
a – одинаковые стороны треугольника
b – основание
α – равные углы при основании
β – угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L – высота=биссектриса=медиана
a – сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M – медиана
R – радиус описанной окружности
O – центр описанной окружности
с – гипотенуза
a, b – катеты
α – острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Как найти сторону треугольника, если известна его медиана и сторона
Информации о медиане и одной из сторон треугольника достаточно для нахождения его другой стороны, если он равносторонний или равнобедренный. В остальных случаях для этого необходимо знать угол между медианой и высотой.
Инструкция
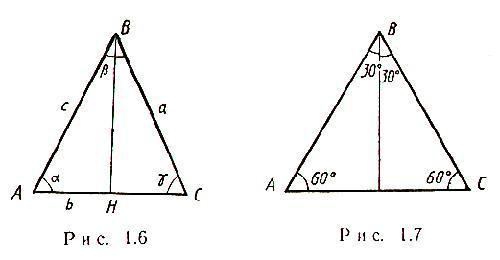
Наиболее простой случай возникает, когда в условии задачи дан равнобедренный треугольник с некоторой стороной a. Две боковые стороны такого треугольника равны, а все медианы пересекаются в одной точке. Кроме того, медиана в равнобедренном треугольнике, проведенная к основанию, является и высотой, и биссектрисой. Соответственно, в треугольнике ABC возникнет треугольник BHC, и по теореме Пифагора можно будет вычислить HC – половину стороны AC:HC=√[(CB)^2-(BH)^2]Следовательно, AC=2√[(CB)^2-(BH)^2]В равнобедренном треугольнике угол α=γ, как это показано на рисунке.
Если в условии задачи приведено значение длины медианы равнобедренного треугольника, проведенной к его боковой стороне, решайте задачу несколько иным способом. Во-первых, медиана не перпендикулярна к боковой стороне фигуры, а во-вторых, формула зависимости между медианой и тремя сторонами выглядит следующим образом:ma=√2(c^2+b^2)-a^2По этой формуле найдите ту сторону, которую медиана делит пополам.
Если треугольник является неправильным, то информации о медиане и стороне недостаточно. Необходимо знать также угол между медианой и стороной. Чтобы решить задачу, вначале найдите по теореме косинусов половину стороны треугольника:c^2=a^2+b^2-2ab*cosγ, где c – сторона, которую нужно найти.Если получается так, что используя теорему косинусов, можно найти лишь только половину стороны, то тогда вычисляемое значение умножается на два. Например, дана медиана и прилежащая к ней сторона, между которыми находится угол. Противоположная углу сторона делится медианой пополам. Вычислив половину стороны по теореме косинусов, получим:BC = 2c, где c – 1/2 стороны BC
Решение прямоугольных треугольников является таким же, как и у любого неправильного треугольника, если нам не известны его углы, а дан лишь только угол между медианой и стороной. Узнав вторую сторону, уже можно найти и третью по теореме Пифагора. Такие задачи помогают искать помимо сторон и другие параметры треугольников. К ним относятся, например, площадь и периметр, которые вычисляются по заданным сторонам и углам.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
