Прямоугольный треугольник. Вычисление сторон и углов. Задание В7 (2015
Для решения задач на нахождение сторон и углов прямоугольного треугольника нужно вспомнить определения синуса, косинуса и тангенса.
Рассмотрим прямоугольный треугольник:
 Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Противолежащий катет – это тот катет, который лежит напротив угла, синус которого мы рассматриваем.
Например, для треугольника, который изображен на рисунке,  ,
, 
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Прилежащий катет – это тот катет, который является одной из сторон угла, косинус которого мы рассматриваем.
Например, для треугольника, который изображен на рисунке,  ,
, 
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Например, для треугольника, который изображен на рисунке,  ,
, 
Задачи на нахождение сторон и углов прямоугольного треугольника решаются по такому алгоритму:
1. Выделяем треугольник, в который входит сторона или угол, который нам нужно найти.
2. Смотрим, какие элементы треугольника нам известны, и с помощью какой тригонометрической функции они между собой связаны.
3. Записываем соотношение, которое связывает между собой эти элементы,
Рассмотрим примеры решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике:
1. Задание В7 (№ 27217) В треугольнике  угол
угол 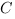 равен
равен 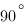 ,
,  . Найдите
. Найдите 

рис.1
Решим эту задачу двумя способами.
а. Так как требуется найти косинус угла, синус которого известен, мы можем воспользоваться основным тригонометрическим тождеством.


б. 
Введем единичный отрезок  , тогда
, тогда  ,
, 
По теореме Пифагора  .
.
Тогда 
Ответ: 
2. Задание В7 (№27220)
В треугольнике ABC угол C равен 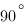 ,
,  . Найдите
. Найдите 
Смотрим на рис.1:

Значит, 
Ответ: 
3. Задание В7 (№27221)
В треугольнике ABC угол C равен 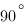 ,
,  . Найдите
. Найдите 

Введем единичный отрезок  , тогда
, тогда  ,
, 
По теореме Пифагора 




Ответ: 
4. Задание В7 (№27221)
В треугольнике ABC угол C равен 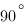 ,
,  ,
,  . Найдите AC.
. Найдите AC.


Введем единичный отрезок  , тогда
, тогда  ,
, 
По теореме Пифагора 
Найдем  :
:  – по условию.
– по условию.
Значит,  . Отсюда
. Отсюда 
Ответ: 
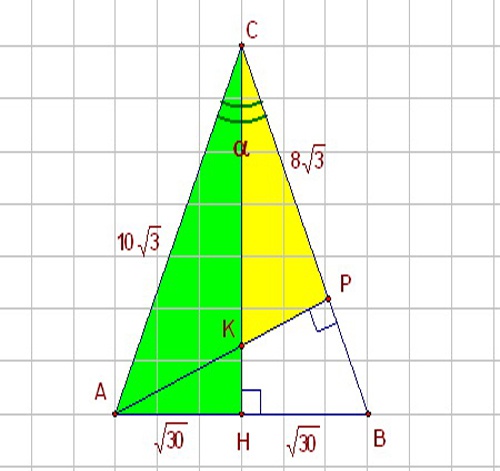
5. Задание В7 (№27259)
В треугольнике ABC угол C равен 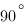 ,
,  ,
,  . Найдите AH.
. Найдите AH.

Найдем  из треугольника
из треугольника 
 – прилежвщий к углу
– прилежвщий к углу  катет, поэтому он связан с
катет, поэтому он связан с  через
через 
Найдем  с помощью основного тригонометрического тождества:
с помощью основного тригонометрического тождества:

 , отсюда
, отсюда 
Теперь рассмотрим треугольник  , в котором
, в котором  – гипотенуза, а
– гипотенуза, а  – катет, связанные между собой через
– катет, связанные между собой через  :
:
 , отсюда
, отсюда 
Ответ: AH=15.
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр “Час ЕГЭ”, попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.
Купить видеокурс “ВСЯ ГЕОМЕТРИЯ. Часть В”
Найти сторону треугольника через синус
Неверно введено число.
Неверно задан треугольник.
Стороны треугольника: теорема синусов
Введите стороны треугольника :
| a | = | |
| β | = | – в градусах |
| γ | = | – в градусах |
Количество знаков после разделителя дроби в числах:
Теория
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Если известны одна сторона и два прилежащих угла, то с помощью теоремы синусов можно вычислить остальные две стороны треугольника. Например пусть известны сторона a и углы γ и β. С учетом того, что сумма всех углов треугольника равна 180 градусов, угол α будет равен:
Тогда остальные стороны вычисляются по следующим формулам:
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Теорема синусов

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° – α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° – α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° – α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° – 60°) = sin60° = 3/√2;
- sin150° = sin(180° – 30°) = sin30° = 1/2;
- sin135° = sin(180° – 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° – α)
Так как sin(180° – α) = sinα, то sinγ = sin(180° – α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° – 45° – 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
[spoiler title=”источники:”]
http://www-formula.ru/2011-10-09-11-08-41
http://skysmart.ru/articles/mathematic/teorema-sinusov
[/spoiler]
Как найти сторону через синус
Сторону треугольника можно найти не только по периметру и площади, но и по заданной стороне и углам. Для этого используются тригонометрические функции – синус и косинус. Задачи с их использованием встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.
Инструкция
Если известна одна из сторон треугольника и угол между ней и другой его стороной, воспользуйтесь тригонометрическими функциями – синусом и косинусом. Представьте себе прямоугольный треугольник НBC , у которого угол α равен 60 градусам. Треугольник НBC показан на рисунке. Поскольку синус, как известно, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь следующим соотношением между этими параметрами:sin α=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу следующим образом:НB=BC*sin α
Если в условии задачи, наоборот, дан катет треугольника, найдите его гипотенузу, руководствуясь следующим соотношением между заданными величинами:BC=НB/sin αПо аналогии найдите стороны треугольника и с использованием косинуса, изменив предыдущее выражение следующим образом:cos α=НC/BC
В элементарной математике существует понятие теоремы синусов. Руководствуясь фактами, которые описывает данная теорема, также можно найти стороны треугольника. Помимо этого, она позволяет найти стороны треугольника, вписанного в окружность, если известен известен радиус последней. Для этого воспользуйтесь соотношением, указанным ниже:a/sin α=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда известны две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.
Помимо теоремы синусов, существует и аналогичная ей по сути теорема косинусов, которая, как и предыдущая, также применима к треугольникам всех трех разновидностей: прямоугольному, остроугольному и тупоугольному. Руководствуясь фактами, которые доказывают эта теорема, можно находить неизвестные величины, используя следующие соотношения между ними:c^2=a^2+b^2-2ab*cos α
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a, b, c – стороны произвольного треугольника
α, β, γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):

Есть следующие формулы для определения катета или гипотенузы

a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):


Формулы сторон по теореме Пифагора, (a,b):



Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b):


Формулы длины равных сторон , (a):


Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
 H – высота треугольника
H – высота треугольника
a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через стороны и радиус, (H):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):


L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):


Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b – катеты прямоугольного треугольника
с – гипотенуза
α – угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L – биссектриса, отрезок ME , исходящий из острого угла
a, b – катеты прямоугольного треугольника
с – гипотенуза
α, β – углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):


Формула длины биссектрисы через катет и гипотенузу, (L):


L – высота = биссектриса = медиана
a – одинаковые стороны треугольника
b – основание
α – равные углы при основании
β – угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):



Формула высоты, биссектрисы и медианы, через стороны, (L):

Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L – высота=биссектриса=медиана
a – сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана
R – радиус описанной окружности
O – центр описанной окружности
с – гипотенуза
a, b – катеты
α – острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет


где a и b – катеты, с – гипотенуза.
2) Найти гипотенузу по двум катетам


где a и b – катеты, с – гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу


где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол


где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними


где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании


где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.
3) Найти боковые стороны по углу между ними


где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании


где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь


где a – искомая сторона, S – площадь треугольника.
2) Найти сторону через высоту


где a – искомая сторона,h – высота треугольника.
3) Найти сторону через радиус вписанной окружности


где a – искомая сторона,r – радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности


где a – искомая сторона,R – радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)


где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)


где a – искомая сторона, b – известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word

