В выпуклом пятиугольнике две стороны равны, третья сторона на 3 см больше, а четвертая в 2 раза больше первой стороны, пятая – на 4 см меньше четвертой. Найдите стороны пятиугольника, если известно, что его периметр равен 34 см.
Светило науки – 826 ответов – 14867 раз оказано помощи
Решай уравнением.
По х см – длина 1 и 2 сторон, (х+3) см – длина 3 стороны, 2х см – длина 4 стороны, (2х-4) см – длина 5 стороны.
Уравнение х+х+(х+3) + 2х + (2х-4) = 34
7х-1=34, х=5 см
Ответ 5 см, 5 см, 8 см, 10 см, 6 см.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,651 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,893 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Найдите длину стороны пятиугольника, если известно, что все его стороны конгруэнтны, а периметр равен 1, 8 дм.
Перед вами страница с вопросом Найдите длину стороны пятиугольника, если известно, что все его стороны конгруэнтны, а периметр равен 1, 8 дм?, который относится к
категории Математика. Уровень сложности соответствует учебной программе для
учащихся 5 – 9 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.
Как определить длину сторон правильного пятиугольника, вписанного в окружность?
дима пикалов
Ученик
(201),
на голосовании
10 лет назад
Дан пятиугольник, вписанный в окружность. Известно, что R данной окружности равен 2. Как узнать длину стороны пятиугольника?
Голосование за лучший ответ
А.К. (лично)
Искусственный Интеллект
(247050)
10 лет назад
5 сторон, значит 360 / 5 = 72 градуса
каждый треугольник равнобедренный с катетами 2 и 2
считай по теореме косинусов 1 грань пятиугольника = корень (2*2 +2*2 – 2*2*2*cos 72)
и умножай ее на 5, коли 5 сторон
———————————————————————
вот как я тебе в свои 51 год решил….
Знай ка
Мудрец
(11288)
10 лет назад
Это потому, что нас при “плохой” Советской Власти учили хорошо и бесплатно. Государству нужны были Специалисты.. .
Дима Пикалов! А кто же поможет потом, когда наше поколение уйдёт?
Длина стороны правильного многоугольника
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Длина стороны пятиугольника вписанного в окружность
Правильный пятиугольник: необходимый минимум информации
Толковый словарь Ожегова гласит, что пятиугольник представляет собой геометрическую фигуру, ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).
Чем интересен правильный пятиугольник?
Основные свойства и формулы
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.
- Центральный угол α = 360 / n = 360/5 =72°.
- Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
- Отношение диагонали к боковой стороне равно (1+√5) /2, то есть «золотому сечению» (примерно 1,618).
- Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:
- если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
- в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
- бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.
- Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
- если имеется вписанная или описанная окружность, то используется одна из двух формул:
S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;
- площадь можно также определить, зная лишь длину боковой стороны а:
S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .
Правильный пятиугольник: построение
1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.
2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.
3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.
4. На середине расстояния между точками О и В постройте точку С.
5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.
6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.
7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить точкой G.
8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.
9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!
Длина стороны правильного многоугольника
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
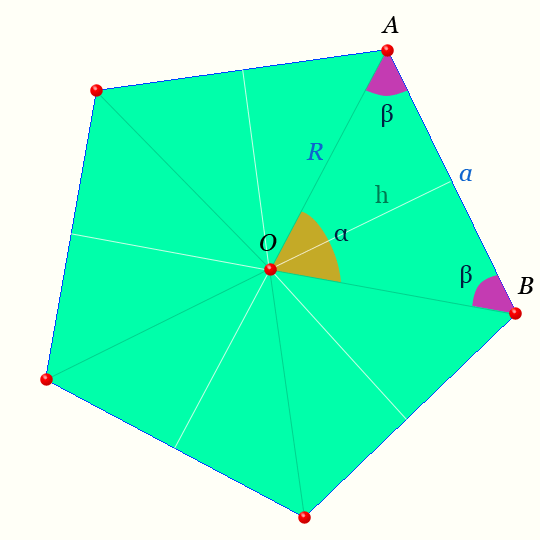
Правильный пятиугольник
Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.
Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного пятиугольника.
Обозначения на рисунке для правильного пятиугольника
| n=5 | число сторон и вершин правильного пятиугольника, | шт |
|---|---|---|
| α | центральный угол правильного пятиугольника, | радианы, ° |
| β | половина внутреннего угла правильного пятиугольника, | радианы, ° |
| γ | внутренний угол правильного пятиугольника, | радианы, ° |
| a | сторона правильного пятиугольника, | м |
| R | радиусы правильного пятиугольника, | м |
| p | полупериметр правильного пятиугольника, | м |
| L | периметр правильного пятиугольника, | м |
| h | апофемы правильного пятиугольника, | м |
Основные формулы для правильного пятиугольника
Периметр правильного пятиугольника
Полупериметр правильного пятиугольника
Центральный угол правильного пятиугольника в радианах
Центральный угол правильного пятиугольника в градусах
Половина внутреннего угла правильного пятиугольника в радианах
Половина внутреннего угла правильного пятиугольника в градусах
Внутренний угол правильного пятиугольника в радианах
Внутренний угол правильного пятиугольника в градусах
Площадь правильного пятиугольника
Отсюда получим апофему правильного пятиугольника
Правильный пятиугольник: необходимый минимум информации
Толковый словарь Ожегова гласит, что пятиугольник представляет собой геометрическую фигуру, ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).
Чем интересен правильный пятиугольник?
Основные свойства и формулы
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.
- Центральный угол α = 360 / n = 360/5 =72°.
- Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
- Отношение диагонали к боковой стороне равно (1+√5) /2, то есть “золотому сечению” (примерно 1,618).
- Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:
- если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
- в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
- бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.
- Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
- если имеется вписанная или описанная окружность, то используется одна из двух формул:
S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;
- площадь можно также определить, зная лишь длину боковой стороны а:
S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .
Правильный пятиугольник: построение
1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.
2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.
3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.
4. На середине расстояния между точками О и В постройте точку С.
5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.
6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.
7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить точкой G.
8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.
9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/dlina-storony-pyatiugolnika-vpisannogo-v-okruzhnost
http://fb.ru/article/58818/pravilnyiy-pyatiugolnik-neobhodimyiy-minimum-informatsii
[/spoiler]