Как найти сторону пятиугольника формула

Длина стороны правильного многоугольника

Определение длины стороны правильного многоугольника по радиусу вписанной окружности

От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».

Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.

Правильный пятиугольник – построение, свойства и формулы

Точное построение фигуры

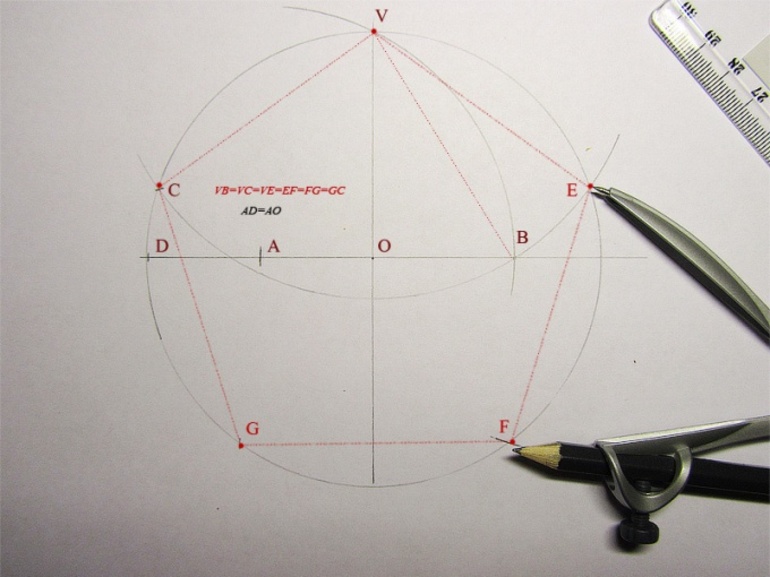
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

1. Построить окружность с центром в некоторой точке О.
2. Провести два диаметра. Они должны пересекаться под прямым углом.
3. Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.
4. По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.
5. Отметить на отрезке OD точку А, которая делит его пополам.
6. Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.
7. Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.
8. Нарисовать окружность с радиусом, равным CV, из точки V.
9. Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).
10. Поставить иглу циркуля в точку F и провести окружность через Е.
11. Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.
12. Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).
13. Соединить пять точек (СVEFG) между собой с помощью линейки.

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Алгоритм Биона

Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

1. Начертить окружность с центром в точке О и радиусом R.
2. Провести в ней диаметр АD.
3. Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.
4. Поделить диаметр на несколько равных частей (АС = СE = ED), количество которых вычисляется по формуле: (n – 2). Переменная “n” эквивалентна количеству граней правильного многоугольника, то есть n = 3. Соотношение можно записать следующей зависимостью: АС = [1 / (n – 2)] * AD = AD / 3.
5. Провести из точек С и Е прямые, перпендикулярные диаметру.
6. Точки пересечения прямых с окружностью обозначить F и G.
7. Если соединить точки, то получится пентагон ABDFG.

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.

Приближенные методы

Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).

Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

1. Начертить произвольную окружность с центром в точке О.
2. Не вынимая иглу циркуля из точки О, выполнить построение другой окружности. Ее радиус нужно уменьшить таким образом, чтобы общий радиус R был равен стороне пятиугольника.
3. Отметить на окружности с большим радиусом две произвольные точки. При этом следует руководствоваться правилом: прямая, проходящая через них, должна касаться малой окружности в одной точке (касательная).
4. Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.
5. Аналогично проделать операции с другими сторонами пентагона.

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.

Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

1. Стороны равны между собой.
2. Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

1. Равенство сторон.
2. Углы равны по 108 градусов.
3. Центры вписанной и описанной окружностей совпадают.
4. Сумма внутренних углов равна 180 * (5 – 2) = 540 (градусов), а внешних – 360.
5. Количество диагоналей соответствует 5.
6. Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.
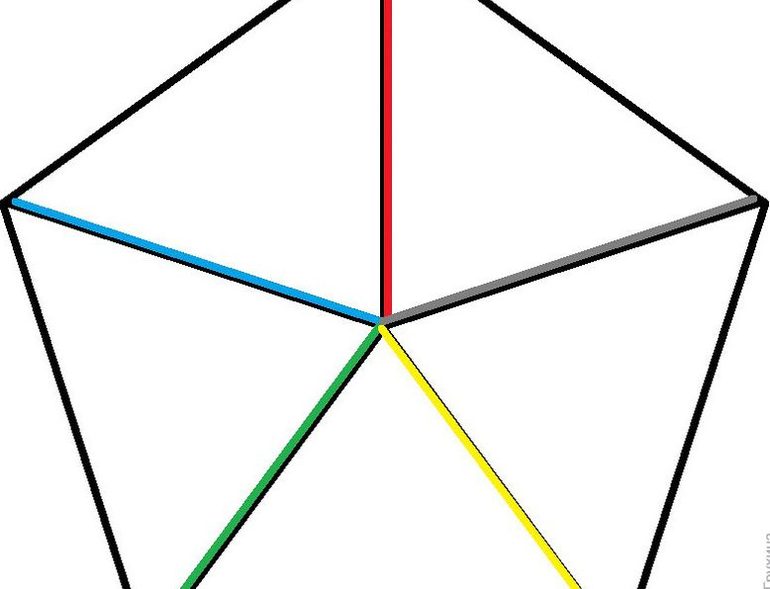
7. Биссектрисы, проведенные через центр, равны.
8. Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.
9. Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.

Расчет параметров

С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.

Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.

Условные обозначения

Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:

1. Сторона: a.
2. Радиус вписанной и описанной окружностей: r и R соответственно.
3. Площадь: S.
4. Периметр и полупериметр: P и p соответственно.
5. Диагональ: d.
6. Отношение золотого сечения: Ф.

Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).

Соотношения и формулы

После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:

Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:

Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:

Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:

1. S = (5a^2 / 4) * ctg(36).
2. S = 5r^2 * tg(36).
3. S = 2,5 * R^2 * sin(72).
4. S = (5/12) * R * d.

Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.

Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).

Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.

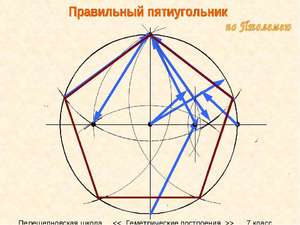
Как построить и нарисовать правильный пятиугольник по окружности

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

• сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
• внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

• если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
• Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
• При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

• с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
• описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
• в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

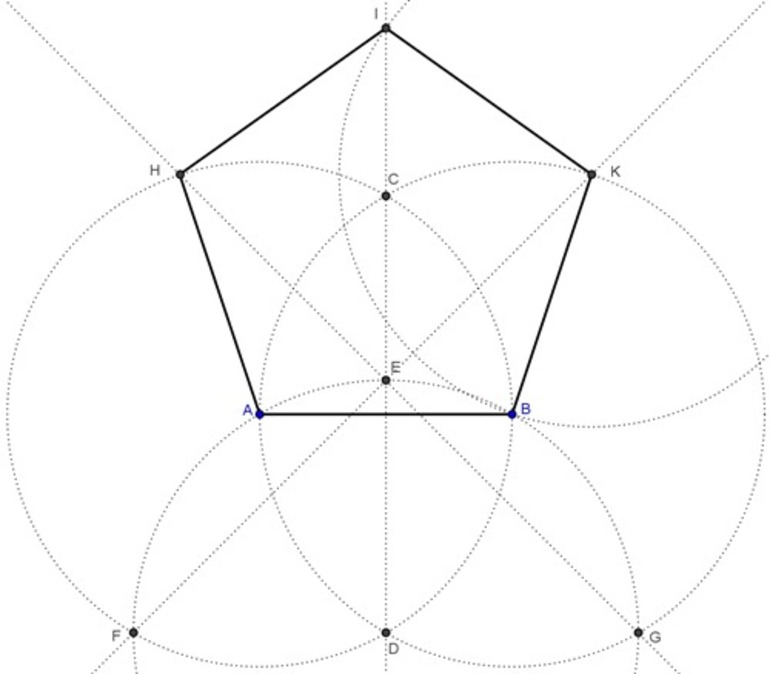
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

[spoiler title=”источники:”]

http://nauka.club/matematika/geometriya/pravilnyy-pyatiugolnik.html

http://liveposts.ru/articles/education-articles/matematika/kak-postroit-i-narisovat-pravilnyj-pyatiugolnik-po-okruzhnosti

[/spoiler]

Где найти формулы для правильного пятиугольника?

Последнее редактирование ответа: 20.10.2011

• 
  Оставить отзыв

  Оставить отзыв

  Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!

  Если Вы хотите получить уведомление об
  исправлении ответа укажите свой e-mail:

  Неправильный формат адреса электронной почты

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 ноября 2020 года; проверки требуют 22 правки.

Иное название этого понятия — «Пентагон»; см. также другие значения.

Пятиугольник
Правильный пятиугольник
Тип	Правильный многоугольник
Рёбра	5
Символ Шлефли	{5}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D5)
Площадь
Внутренний угол	108°
Свойства
выпуклый, вписанный, Равносторонний, равноугольный[en], изотоксальный
Медиафайлы на Викискладе

Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства[править | править код]

• У правильного пятиугольника угол равен

• Площадь правильного пятиугольника рассчитывается по любой из формул:

,

где  — радиус описанной окружности,  — радиус вписанной окружности,  — диагональ,  — сторона.

• Высота правильного пятиугольника:

• Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу .

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

• Сторона:

• Радиус вписанной окружности:

• Радиус описанной окружности:

• Диагональ:

• Площадь:

• Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
• Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)

где  — отношение золотого сечения.

Построение[править | править код]

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.

• Построение правильного пятиугольника

• 

  Построение правильного пятиугольника

• 

  Построение правильного пятиугольника

• 

  Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги[править | править код]

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе[править | править код]

В природе не существует кристаллов с гранями в форме правильного пятиугольника, но исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K
показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.^[1]
Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.

• 

  Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская

Интересные факты[править | править код]

Этот раздел представляет собой неупорядоченный список разнообразных фактов о предмете статьи. Пожалуйста, приведите информацию в энциклопедический вид и разнесите по соответствующим разделам статьи. Списки предпочтительно основывать на вторичных обобщающих авторитетных источниках, содержащих критерий включения элементов в список. (24 июля 2020)

• Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
• Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
• Правильный пятиугольник со всеми его диагоналями является проекцией правильного пятиячейника (4-симплекса).
• Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.

См. также[править | править код]

• Золотое сечение
• Пятиугольник
• Пентаэдр
• Пентаграмма
• Государственный знак качества СССР

Примечания[править | править код]

Пятиугольник, виды, свойства и формулы.

Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.

Пятиугольник, выпуклый и невыпуклый пятиугольник

Правильный многоугольник

Свойства правильного пятиугольника

Построение правильного пятиугольника

Формулы правильного пятиугольника

Правильный пятиугольник в природе, технике и культуре

Пятиугольник, шестиугольник, семиугольник, восьмиугольник

Пятиугольник, выпуклый и невыпуклый пятиугольник:

Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.

Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).

Пятиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый пятиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 540°.

Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.

Рис. 2. Невыпуклый пятиугольник

Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.

Правильный многоугольник:

Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.

Рис. 3. Правильный пятиугольник

Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.

Углы правильного семиугольника образуют семь равнобедренных треугольников.

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.

Свойства правильного пятиугольника:

1. Все стороны правильного пятиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅.

2. Все углы равны между собой и каждый угол равен 108°.

α₁ = α₂ = α₃ = α₄ = α₅ = 108°.

Рис. 4. Правильный пятиугольник

3. Сумма внутренних углов правильного пятиугольника равна 540°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.

Рис. 5. Правильный пятиугольник

5. Количество диагоналей правильного пятиугольника равно 5.

Рис. 6. Правильный пятиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр пятиугольника O.

Рис. 7. Правильный пятиугольник

7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.

Рис. 8. Правильный пятиугольник

8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.

a / c ≈ 5 / 8 ≈ 0,618.

Рис. 9. Правильный пятиугольник

Построение правильного пятиугольника:

Метод построения правильного пятиугольника вписыванием его в заданную окружность:

1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.

2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.

3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.

4. Постройте точку C посередине между O и B.

5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.

6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.

7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.

8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.

9. Постройте правильный пятиугольник AEGHF.

Формулы правильного пятиугольника:

Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.

Формулы площади правильного пятиугольника:

Формулы высоты правильного пятиугольника:

Формулы стороны правильного пятиугольника:

Формулы диагонали правильного пятиугольника:

Формулы радиуса окружности, вписанной в правильный пятиугольник:

Формулы радиуса окружности, описанной вокруг правильного пятиугольника:

Правильный пятиугольник в природе, технике и культуре:

Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.

Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.

Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.

Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.

Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Пятиугольник

Шестиугольник

Семиугольник

Восьмиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
9 622

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

• Расчет длины стороны
  • Через радиус вписанной окружности

  • Через радиус описанной окружности

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Через радиус вписанной окружности

Формула расчета

Через радиус описанной окружности

Формула расчета