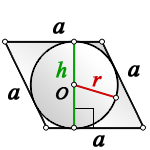
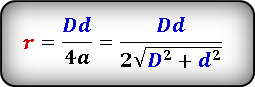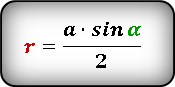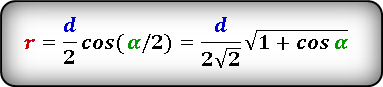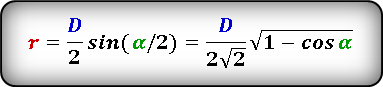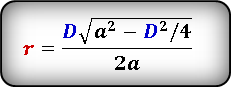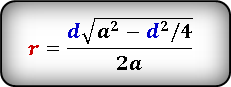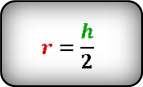В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.
-
Формулы вычисления радиуса вписанной в ромб окружности
- Через диагонали и сторону
- Через диагонали
-
Через сторону и угол
- Через высоту
- Примеры задач
Формулы вычисления радиуса вписанной в ромб окружности
Через диагонали и сторону
Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.
- d1 и d2 – диагонали ромба;
- a – сторона ромба.
Через диагонали
Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:
Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):
Через сторону и угол
Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.
Через высоту
Радиус вписанного в ромб круга равняется половине его высоты.
- h (или GF) – высота ромба;
- h = 2r.
Примеры задач
Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.
Решение
Применим соответствующую формулу, подставив в нее известные значения:
Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.
Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:
Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a – сторона ромба
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
Сторона ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
1. Сторона ромба через высоту и площадь
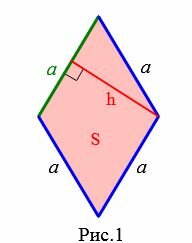
Пусть известны площадь и высота ромба (Рис.1).
Покажем, что сторона ромба через высоту и площадь вычисляется формулой
| (small a=frac<large S><large h>.) | (1) |
Формула площади ромба через сторону и высоту имеет следующий вид:
Откуда легко вывести формулу (1).
2. Сторона ромба через высоту и угол
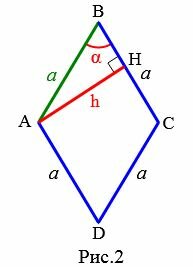
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
Для прямоугольного треугольника AHB применим теорему синусов:
(small frac<large a><large sin 90°>=frac<large h><large sin alpha>.)
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| (small a=frac<large h><large sin alpha>.) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Сторона ромба через диагонали
Выведем формулу вычисления сторон ромба через диагонали.
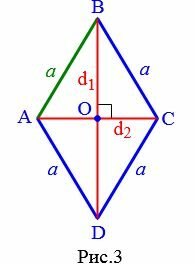
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
Применим к прямоугольному треугольнику AOB теорему Пифагора:
(small a^2= left( frac<large d_1> <large 2>right)^2+left( frac<large d_2> <large 2>right)^2.)
| (small a= frac<sqrt<large d_1^2+d_2^2>> <large 2>) | (3) |
4. Сторона ромба через угол и противолежащую диагональ
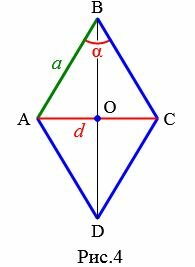
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
| (small a=frac<large d><large 2 cdot sin frac< alpha>< 2>>.) | (4) |
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
| (small sin frac< alpha>< 2>=sqrt<frac<large 1-cos alpha><large 2 >>.) | (5) |
Подставляя (5) в (4), получим:
(small a=frac<large d><large 2 cdot sqrt<frac<large 1-cos alpha><large 2 >>>.)
| (small a=large frac< d>< sqrt< 2-2 cdot cos alpha>>.) | (6) |
5. Сторона ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
| (small frac<large OB > <large a>=cos angle ABO.) | (7) |
Учитывая, что ( small BO=frac<large d><large 2>) и ( small angle ABO=frac<large alpha><large 2>), формулу (13) можно записать так:
(small frac< large frac<large d > <large 2>><large a>= cos frac<large alpha> <large 2>.)
| (small a=frac<large d><large 2 cdot cos large frac< alpha>< 2>>.) | (8) |
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
| (small cos frac< alpha>< 2>=sqrt<frac<large 1+cos alpha><large 2 >>.) | (9) |
Подставляя (9) в (8), получим:
(small a=frac<large d><large 2 cdot sqrt<frac<large 1+cos alpha><large 2 >>>.)
| (small a=large frac< d>< sqrt< 2+2 cdot cos alpha>>.) | (10) |
6. Сторона ромба через площадь и радиус вписанной в ромб окружности
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
| (small S= 2 cdot a cdot r.) | (11) |
Из формулы (11) получим:
| ( small a=frac<large S> <large 2 cdot r>) | (12) |
7. Сторона ромба через площадь и угол
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
| (small S= a^2 cdot sin alpha.) | (13) |
Из формулы (13) найдем a:
| ( small a=frac<large S> <large sin alpha>) | (14) |
Получили формулу сторон ромба через площадь и угол.
Ромб. Формулы, признаки и свойства ромба
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 – 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 – 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://matworld.ru/geometry/storona-romba.php
http://ru.onlinemschool.com/math/formula/rhombus/
[/spoiler]
Окружность, вписанная в ромб
Ромб — это параллелограмм с четырьмя равными сторонами.
Квадрат — частный случай ромба; это ромб, все углы которого прямые.
Вписанная в ромб окружность — это окружность, которая лежит внутри ромба и касается всех его сторон.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Окружность можно вписать в многоугольник, у которого равны суммы противолежащих сторон. Ромб соответствует этому условию, поэтому в ромб можно вписать окружность.
Свойства ромба и вписанной окружности
- в любой ромб можно вписать окружность;
- точка пересечения диагоналей ромба является центром окружности, вписанной в ромб.
Как найти радиус, основные способы
Радиус вписанной окружности, если известны диагонали и сторона
Радиус r вписанной в ромб окружности равен произведению его диагоналей, деленному на периметр или на сторону, умноженную на 4.
Формула 1
(r=frac{d_1d_2}Р=frac{d_1d_2}{4a})
где r — радиус вписанной окружности,
d1 и d2 — диагонали ромба,
a — сторона ромба,
Р — периметр ромба.
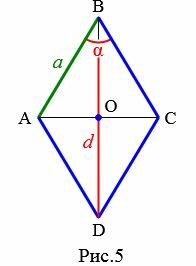
У изображенного ромба АВСD сторона равна а. Большая диагональ BD равна (d_1), меньшая диагональ АС равна (d_2). Радиус вписанной окружности:
(r=frac{d_1d_2}{4a}=frac{BDcdot AC}{4cdot АВ}).
Если известны только диагонали ромба
Формула 2
(r=frac{d_1d_2}{2sqrt{left(d_1right)^2+left(d_2right)^2}})
где r — радиус вписанной окружности,
d1 и d2 — диагонали ромба.
Эту формулу можно получить из предыдущей.
Диагонали ромба пересекаются под прямым углом, делятся точкой пересечения пополам, и разбивают ромб на четыре прямоугольных треугольника.
Рассмотрим один из таких треугольников — ΔАВО. Сторона ромба АВ является гипотенузой ΔАВО.
Если известны диагонали ромба BD, равная (d_1) и АС, равная (d_2), то катеты ВО и АО ΔАВО будут равны (frac{d_1}2) и (frac{d_2}2) соответственно.
Выразим гипотенузу АВ треугольника АВО через его катеты ВО и АО.
Согласно теореме Пифагора (АВ=sqrt{ВО^2+АО^2}=sqrt{left(frac{d_1}2right)^2+left(frac{d_2}2right)^2}).
Подставив в формулу (r=frac{d_1d_2}p=frac{d_1d_2}{4a}) значение (а=sqrt{left(frac{d_1}2right)^2+left(frac{d_2}2right)^2}) и упростив выражение,
получаем (r=frac{d_1d_2}{2sqrt{left(d_1right)^2+left(d_2right)^2}}).
Если известны сторона и угол
Радиус окружности, вписанной в ромб, равен половине произведения его стороны и синуса любого внутреннего угла ромба.
Формула 3
(r=frac{acdotsinalpha}2=frac{acdotsinbeta}2)
где r — радиус вписанной окружности,
α и β — внутренние углы ромба,
a — сторона ромба.
Если известна высота ромба
Радиус вписанной в ромб окружности равен половине его высоты.
Формула 4
(r=frac h2)
где r — радиус вписанной окружности,
h — высота ромба.
Из этой формулы следует, что высота ромба равна диаметру вписанной в него окружности.
Если известны площадь ромба и его сторона
Формула 5
(r=frac S{2a}=frac Sр)
где r — радиус вписанной окружности,
S — площадь ромба,
a — сторона ромба,
р — полупериметр ромба.
Вычисление радиуса через отрезки m и n
Вписанная окружность касается стороны ромба. Точка касания делит сторону ромба на два отрезка. Пусть это будут отрезки m и n.
Диагонали ромба взаимно перпендикулярны, ΔАОD — прямоугольный. Высота ΔАОD к стороне АD равна радиусу вписанной в ромб АВСD окружности.
По свойству высоты прямоугольного треугольника, проведенной к гипотенузе, (ОК=sqrt{АКcdot КD}).
Следовательно, радиус вписанной в ромб окружности равен среднему пропорциональному между отрезками, на которые делит сторону ромба точка касания.
Формула 6
(r=sqrt{mcdot n})
где r — радиус вписанной окружности,
m и n — отрезки, на которые делит сторону ромба точка касания.
Задачи с решениями
Задача 1
Дано: ромб с диагоналями 6 см и 8 см.
Найти: радиус вписанной в ромб окружности.
Решение: так как известны диагонали ромба,
применим формулу (r=frac{d_1d_2}{2sqrt{left(d_1right)^2+left(d_2right)^2}}).
(r=frac{6cdot8}{2sqrt{6^2+8^2}}=2,4 (см).)
Ответ: радиус вписанной в ромб окружности равен 2,4 см.
Задача 2
Дано: ромб, сторона которого равна 16 см, а острый угол ромба — 30°.
Найти: радиус вписанной в ромб окружности.
Решение: применим формулу (r=frac{acdotsinalpha}2.)
(r=frac{16cdot0,5}2=frac82=4 (см).)
Ответ: радиус вписанной в ромб окружности равен 4 см.
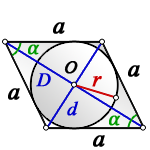
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a – сторона ромба
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
- Подробности
-
Опубликовано: 10 сентября 2011
-
Обновлено: 13 августа 2021
Ромб — это параллелограмм, в котором все стороны являются взаимно одинаковыми. Соответственно, ромб
включает в себя абсолютно все свойствами параллелограмма и является его частным случаем. Также ещё
существуют такие важные факты о ромбе, как например, то что в каждый отдельно взятый ромб можно
включить окружность. Необходимо запомнить, что центр окружности, которая уже включена и находится в
ромбе является точкой, в которой пересекаются абсолютно все существующие диагонали рассматриваемой
фигуры. В то же время, место в котором пересекаются все существующие диагонали является центром
симметрии данного ромба.
- Сторона ромба через площадь ромба и высоту
- Сторона ромба через площадь и синус угла
- Сторона ромба через площадь и радиус вписанной
окружности - Сторона ромба через диагонали
- Сторона ромба через длинную диагональ и острый угол
- Сторона ромба через короткую диагональ и тупой угол
- Сторона ромба через периметр
Через площадь и высоту
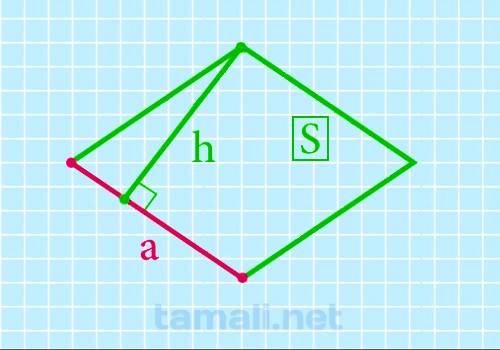
Для того чтобы найти сторону ромба через площадь и высоту, необходимо воспользоваться следующей
формулой:
A = S /h
где S — площадь ромба, h — высота исследуемого ромба.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если площадь равна 30 см, а высота, опущенная на эту сторону — 3 см.
Решение. a=S/ha=30/3=10 см.
Сторона ромба через периметр
Для того чтобы найти одну из сторон ромба через периметр, нужно воспользоваться следующей
формулой:
a = P / 4
где P — периметр ромба.
Цифр после
запятой:
Результат в:
Пример. Периметр ромба равен 28 см. Найти сторону ромба.
Решение. а = 28 / 4 = 7 см.
Через площадь и синус угла
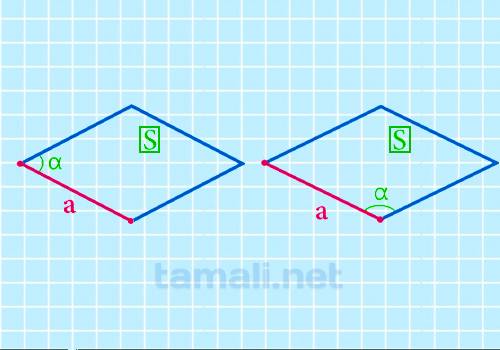
Для нахождения стороны ромба через площадь и синус угла необходимо использовать формулу,
представленную ниже:
a = √S / √sinɑ
где S — площадь ромба, a — сторона ромба, ɑ — острый угол ромба.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если площадь равна 18 см, а острый угол — 30º.
Решение. a = √S/√sinɑ = a² =18/0.5=36 см a= 6 см.
Через площадь и радиус вписанной окружности
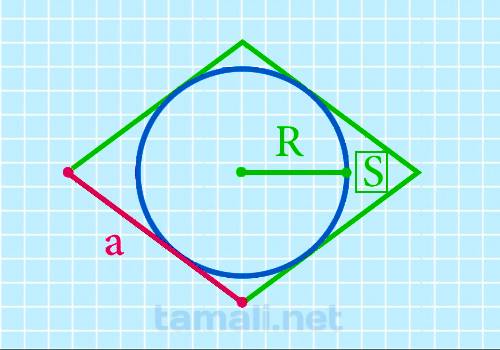
Для того чтобы рассчитать стороны ромба через площадь и радиус вписанной окружности, нужно
воспользоваться следующей формулой:
a = S/2r
где a — сторона ромба, S — площадь, r – радиус.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если радиус вписанной окружности равен 2 см, а площадь — 12 см. a = 12/2*2=3 см.
Через длинную диагональ и острый угол
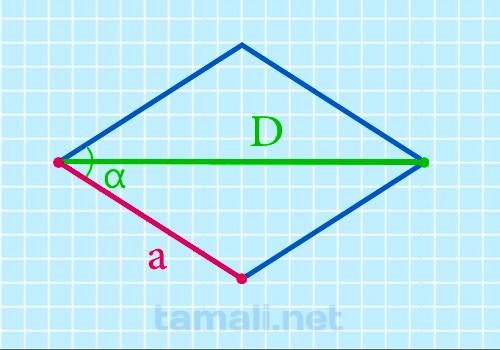
Чтобы найти сторону ромба через длинную диагональ и острый угол следует воспользоваться данной
формулой:
a = D / 2 + 2*cosɑ
где D — длинная диагональ, ɑ — острый угол ромба.
Цифр после
запятой:
Результат в:
Пример. Длинная диагональ ромба равна 12 см, а острый угол — 60º. Найти сторону ромба.
Решение. A= 12/2 + 2*1/2=6+1= 7 см.
Через короткую диагональ и тупой угол
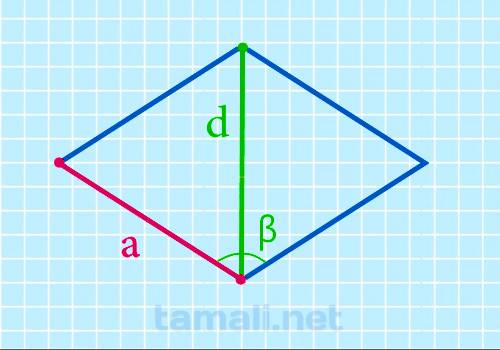
Для того чтобы найти сторону ромба необходимо воспользоваться следующей формулой:
a = d/2 – 2cosβ
где d — короткая диагональ, β — тупой угол ромба.
Цифр после
запятой:
Результат в:
Пример. Тупой угол ромба равен 120º, а короткая диагональ — 6 см. Найти сторону ромба.
Решение: a = 6 / 2 – 2 * (-0.5) = 3 + 1 = 4 см.
Сторона ромба через диагонали
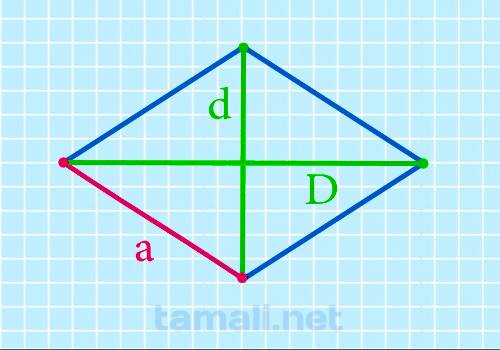
Для нахождения стороны ромба через диагонали необходимо произвести следующие расчёты:
a = D² + d²/2
где a — сторона ромба, которую необходимо найти, D — наибольшая из диагоналей, d – наименьшая
диагональ ромба.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если диагонали равны 24 см и 10 см.
Решение. АС² + ВD² = 2(АВ² + ВС²), 100 + 576 = 4 · АВ²; АВ²= 169; АВ = 13 см. АВ = ВС = СD = АD = 13 см.
Примеры
Пример 1. Длины двух диагоналей d1 и d2 ромба равны 5 и 10 единицам соответственно.
Найдите площадь ромба.
Решение: d1 = 5 единиц и d2 = 10 единиц. Площадь = (d1 × d2) / 2 = (5 ×
10) / 2 квадратных единиц = 25 квадратных единиц.
Пример 2: Длины двух диагоналей d1 и d2 ромба равны 14 и 17 единицам соответственно.
Найдите площадь ромба.
Решение: d1 = 14 единиц и d2 = 17 единиц. Площадь = (d1 × d2) / 2 = (14
× 17) / 2 квадратных единиц = 70 квадратных единиц.
Пример 3: Длины двух диагоналей d1 и d2 ромба равны 3 единицам и 6 единицам
соответственно. Найдите площадь ромба.
Решение: d1 = 3 единицы и d2 = 6 единиц. Площадь = (d1 ×
d2) / 2 = (3 × 6) / 2 квадратных единиц = 9 квадратных единиц.
Стоит подчеркнуть свойство о том, что диагонали в рассматриваемой фигуре будут характеризоваться как
биссектрисы углов ромба, а также, то, что все существующие диагонали представляются
перпендикулярными. Соответственно, все перечисленные определения ромба доказывают, что он имеет
абсолютно все свойства параллелограмма.
Для того чтобы понять природу ромба необходимо также рассмотреть параллелограмм, его определение и
свойства. Параллелограмм представляет из себя четырёхугольник, в котором все стороны, лежащие
напротив друг друга, являются параллельными Ромб — частный случай параллелограмма.
Как и у любой фигуры, у ромба есть различные свойства, которые определяют, что он собой представляет.
К таким свойствам относятся:
- Четыре прямые стороны равной длины (AB = CD = DA = BC)
- Диагонали пересекают друг друга под углом 90°, или можно также сказать, что каждая из двух
диагоналей ромба является перпендикулярной биссектрисой другой (диагонали DB и CA пересекают
друг друга под углом 90°) - Противоположные углы равны, а противоположные стороны параллельны CD || AB и BC || AD; ∠A = ∠C и
∠D = ∠B - Смежные углы в сумме составляют 180° (∠A + ∠B = 180°; ∠B + ∠C = 180°; ∠C + ∠D = 180°; ∠A + ∠D =
180°) - Четыре вершины.
- Две линии симметрии.
- Четыре внутренних угла — два острых и два тупых.
- Две пары параллельных прямых.