Как найти сторону равностороннего треугольника зная основание

Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.

Сторона равностороннего треугольника через радиус описанной окружности

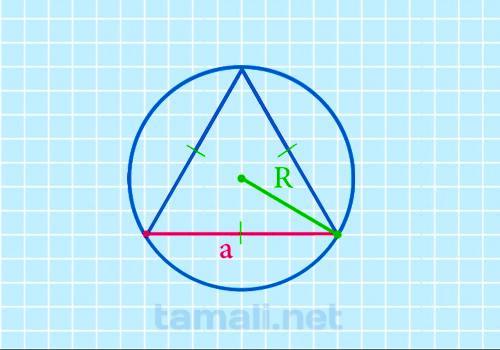
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:

a = R * √3

где а — сторона треугольника, R — радиус описанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.

Сторона равностороннего треугольника через радиус вписанной окружности

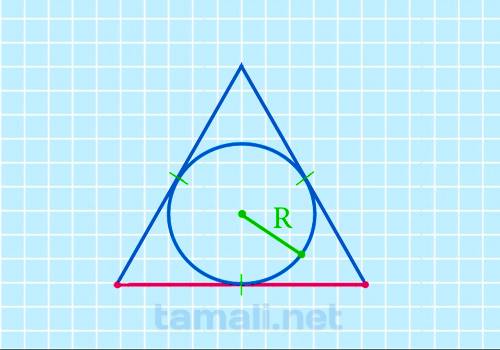
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):

a = 2r * √3

где а — сторона треугольника, R — радиус вписанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.

Сторона равностороннего треугольника через высоту

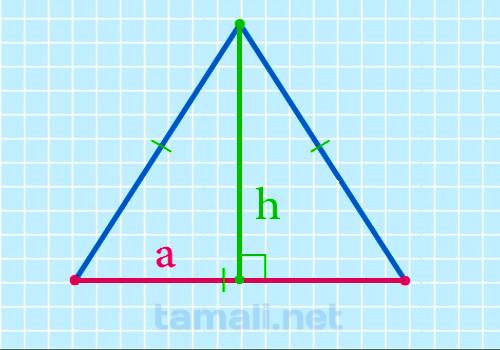
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:

a = 2h / √3

где а — сторона, h —  высота равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.

Сторона равностороннего треугольника через площадь

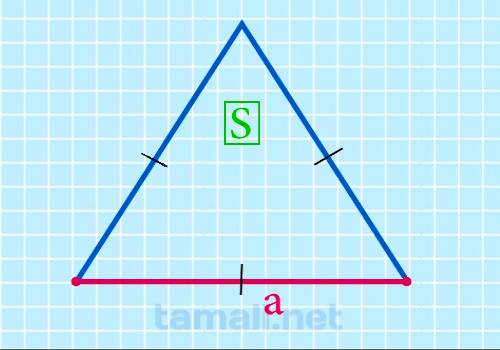
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу

a = √(4S / √3)

где а — сторона, S —  площадь равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.

Основание равнобедренного треугольника через боковые стороны и угол между ними

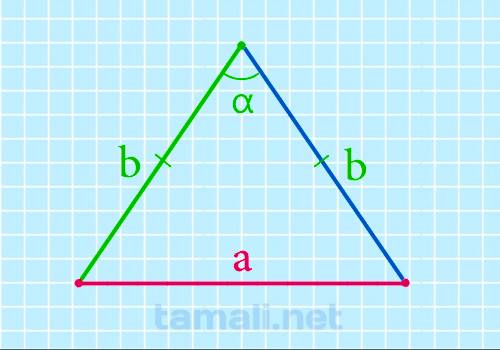
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:

a = 2b * sin (α/2)

где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.

Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.

Основание равнобедренного треугольника через боковые стороны и угол при основании

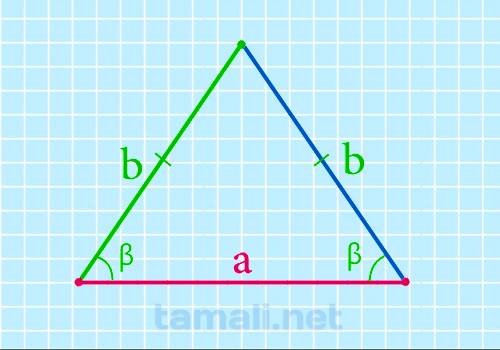
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:

a = 2b + cos β

где b — боковая сторона, β — угол при основании.

Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.

Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами

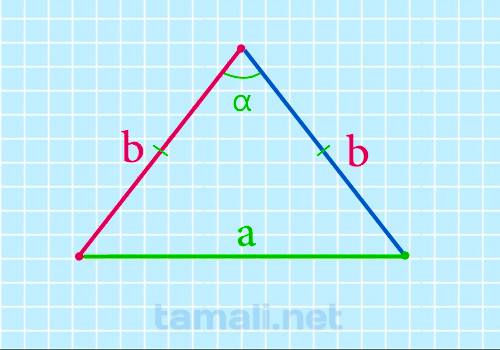
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным.  Это значит, что α = β.

Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:

b = a / (2 * sin(α/2))

где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.

Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.

Боковая сторона равнобедренного треугольника через основание и угол при основании

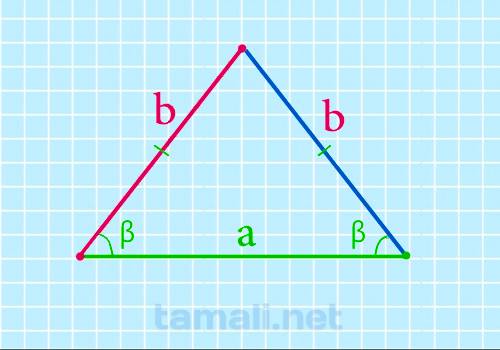
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:

b = a / 2 * cos β

где a — это основание, β — угол при основании равнобедренного треугольника.

Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.

Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.

Катет прямоугольного треугольника через гипотенузу и острый угол

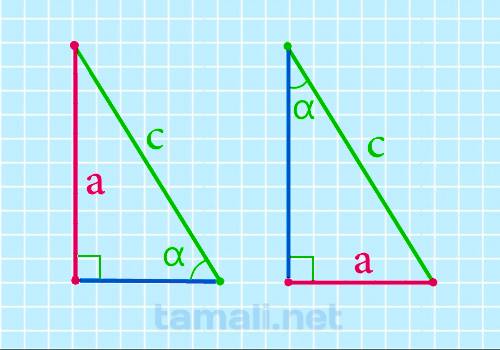
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:

a = c * sin α

где c — гипотенуза, α — острый угол прямоугольного треугольника.

Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее:  a = 77 * 0,98 = 75,8см.

Катет прямоугольного треугольника через гипотенузу и другой известный катет

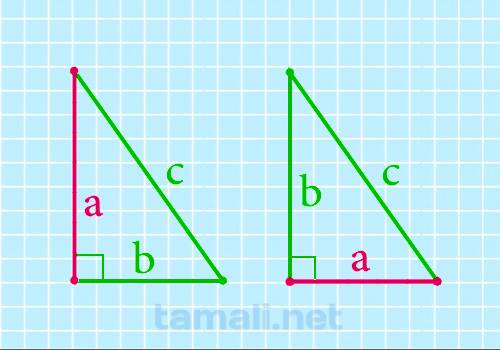
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:

a = √(c² — b²)

где c — гипотенуза, b — катет который известен прямоугольного треугольника.

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см

Гипотенуза прямоугольного треугольника через катет и острый угол

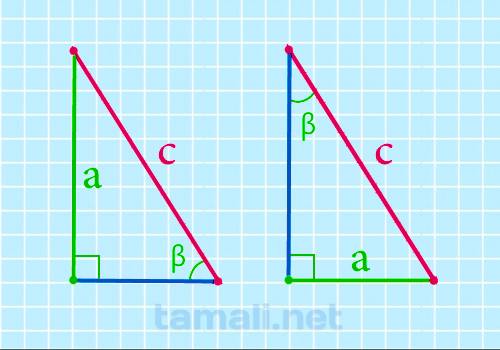
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:

c = a / sin(β)

где a — катет, β — острый угол прямоугольного треугольника.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.

Гипотенуза прямоугольного треугольника через катеты

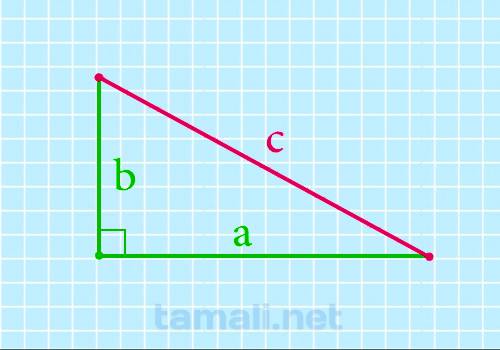
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:

c = √(a² + b²)

где c — гипотенуза, a и b — катеты.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см

Сторона треугольника через две известные стороны и угол между ними

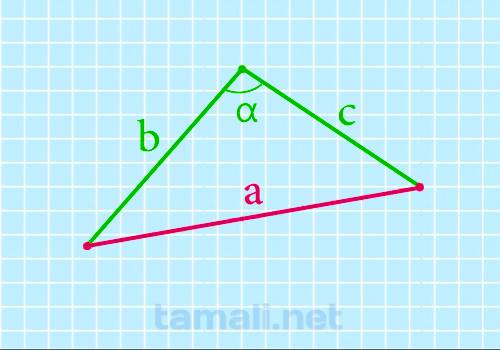
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:

a = b² + c² — 2bc * cos α

где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.

Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.

Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.

Сторона треугольника через известную сторону и два угла

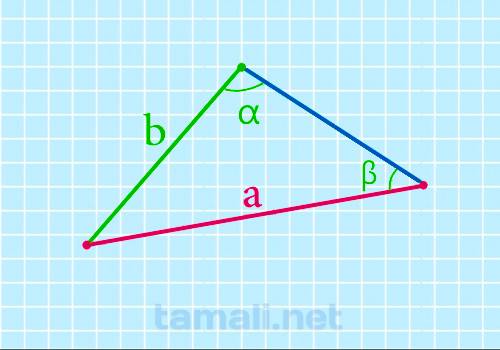
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:

a = (b * sin α) / sin β

где b — сторона треугольника; β, α — углы треугольника.

Пример. Пусть сторона треугольника b равна 10, угол β  = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30   = 8.71723 мм.

Равносторонний треугольник – первый из ряда правильных многоугольников, отличается от остальных треугольников тем, что у него все углы и стороны равны, как видно из названия. Здесь, как и в равнобедренном треугольнике, можно найти сторону, зная высоту, из теоремы Пифагора в получившихся прямоугольных треугольниках. Сторона равностороннего треугольника a в квадрате, как гипотенуза, будет равна сумме квадратов высоты и половины основания, которое также является стороной a:

Стороны равностороннего треугольника

Треугольник, у которого все три стороны равны, называется равносторонним. Периметр такого треугольника равен стороне (а) умноженной на 3 (количество сторон): : P = 3a.
Кроме сторон, у такого треугольника одинаковы и все углы, по 60 градусов каждый, т.к. сумма всех углов треугольника равна 180 градусам. Перпендикуляр, опущенный из вершины треугольника на его противоположную сторону, является его высотой. Она делит треугольник на 2 одинаковых прямоугольных треугольника, у которых гипотенузой будет сторона равностороннего треугольника (а), одним из катетов — высота (h), а другим катетом — половина его основания или (а/2), т.к в треугольнике все стороны равны.
По теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы (в нашем случае она является и стороной равностороннего треугольника) равен сумме квадрата высоты h и квадрата половины основания (половины стороны а):

a 2 = h 2 + a 2 /2 2 ,

где а — сторона, h — высота равностороннего треугольника.
После проведенных преобразований, выводим формулу для расчета стороны равностороннего треугольника по его высоте:

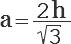
Т.е. сторона равностороннего треугольника (а) равна удвоенной высоте (2h) на корень квадратный из трех.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

[spoiler title=”источники:”]

http://www-formula.ru/2011-10-09-11-08-41

[/spoiler]