Как найти сторону ромба через диагонали формула

Как найти сторону ромба через диагонали формула

Укажите размеры:

Результат:

Решение:

Скопировать

Ссылка на страницу с результатом:

# Теория

Ромб – это параллелограмм у которой все стороны равны, а углы непрямые.

Диагональ ромба – это прямой отрезок соединяющий вершины противоположных углов ромба.

Свойства ромба:

  • Все стороны ромба равны;
  • Диагонали ромба пересикаются под прямым углом;
  • Диагонали ромба в точке пересечения делятся пополам;
  • Сумма углов, прилежащих к одной стороне ромба, равна 180°;
  • Противоположные углы ромба равны.

Как найти сторону ромба через диагонали

D
d
a
a
a
a

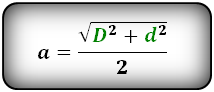
a = dfrac{ sqrt{D^2 + d^2} }{2}

  • a – сторона ромба
  • D – большая диагональ ромба
  • d – меньшая диагональ ромба

Похожие калькуляторы:

Войдите чтобы писать комментарии

Источник

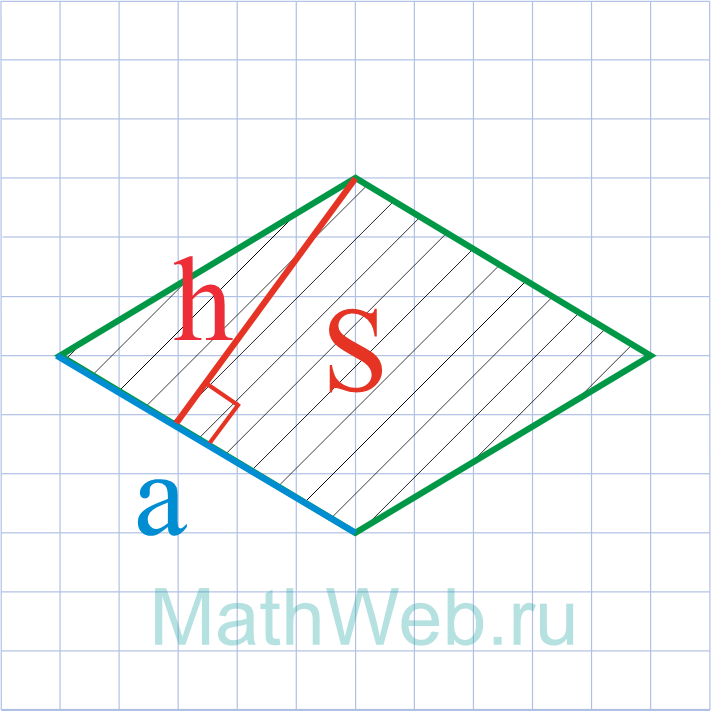
Сторона ромба через площадь ромба и высоту.

Где S – площадь ромба,h – его высота.

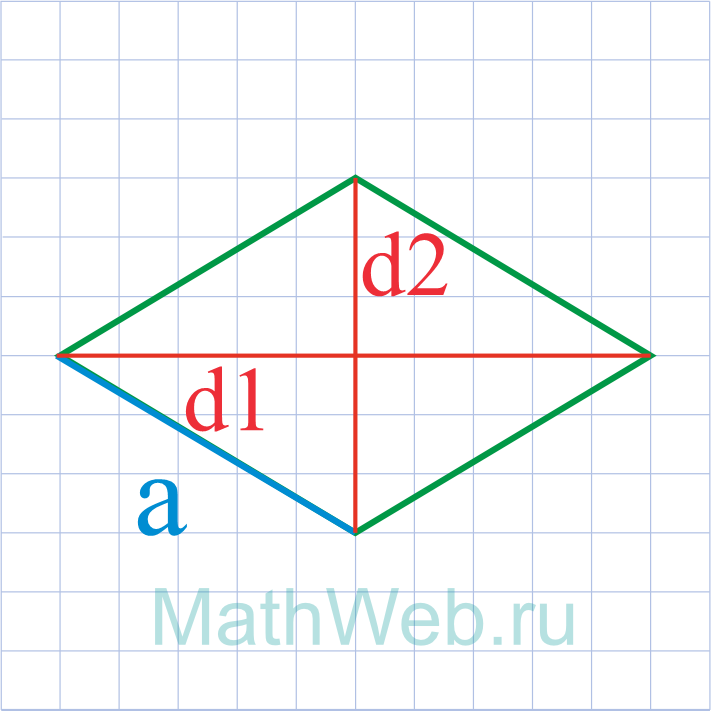
Сторона ромба через диагонали.

Где d1 – большая диагональ,d2 – меньшая диагональ.

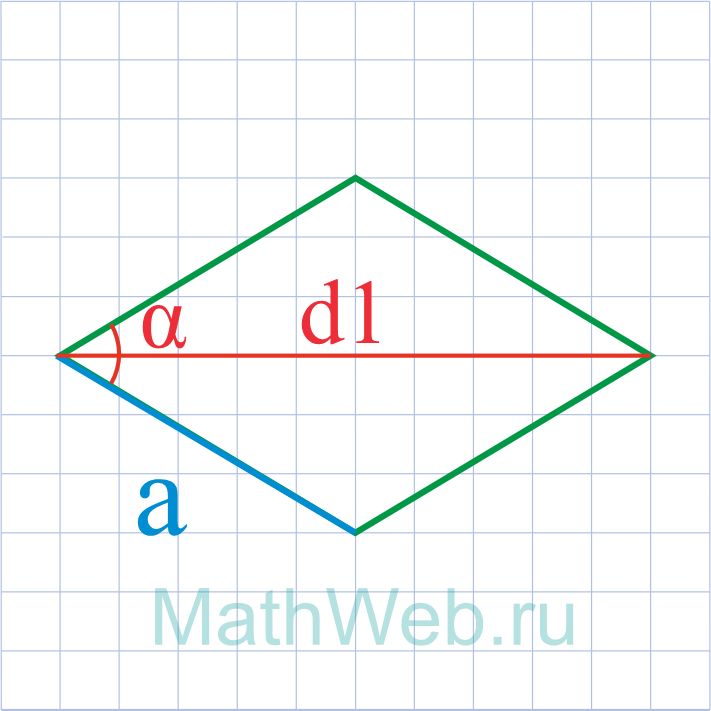
Сторона ромба через длинную диагональ и острый угол.

Где d1 – большая диагональ,α – острый угол.

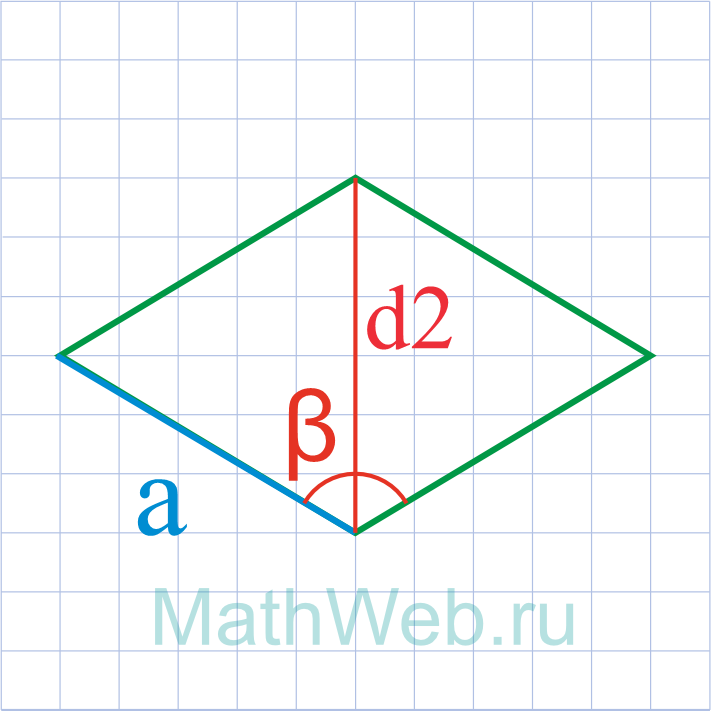
Сторона ромба через короткую диагональ и тупой угол.

Где d2 – меньшая диагональ,β – тупой угол.

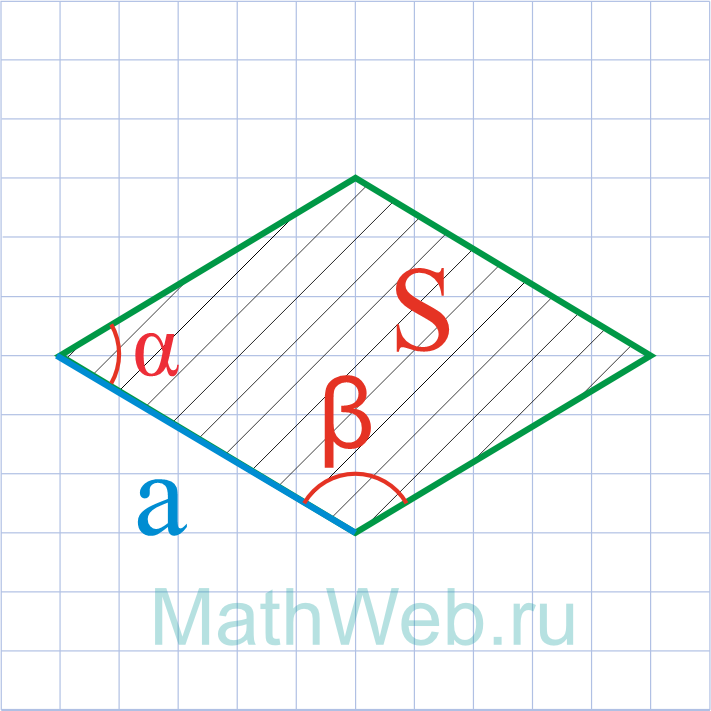
Сторона ромба через площадь и синус угла.

Где S – площадь ромба, α°,β° – его углы.

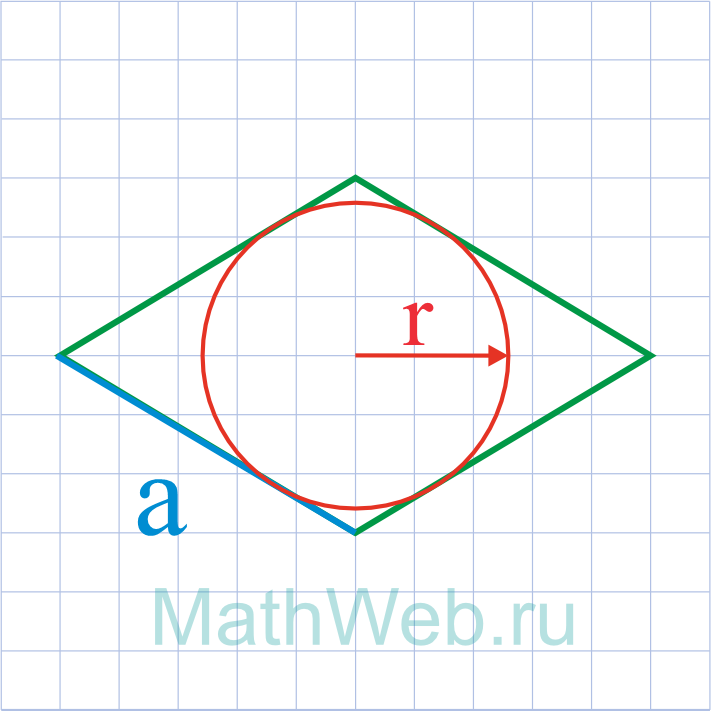
Сторона ромба через площадь и радиус вписанной окружности.

Где S – площадь ромба,r – радиус вписанной окружности.

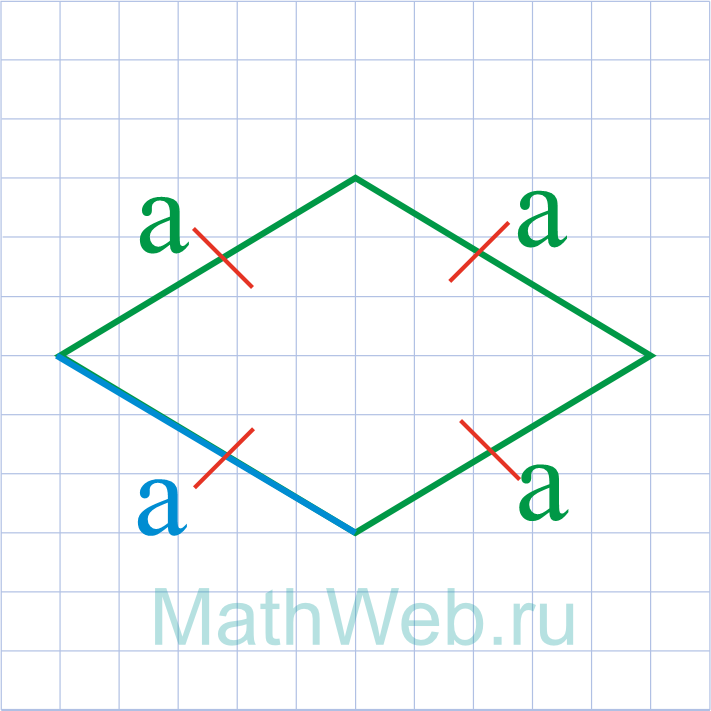
Сторона ромба через периметр.

Где P – периметр ромба.

Ромб

  • Ромб  – это параллелограмм у которого все стороны равны. 
  • Противоположные стороны ромба параллельны.
  • Все ромбы различаются между собой только размером стороны и углов.

Как найти длину стороны ромба?

Сторона ромба может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.

Сторона ромба через площадь ромба и высоту.

a =

S

h
Сторона ромба через диагонали.

a =

√d12 ― d22

2
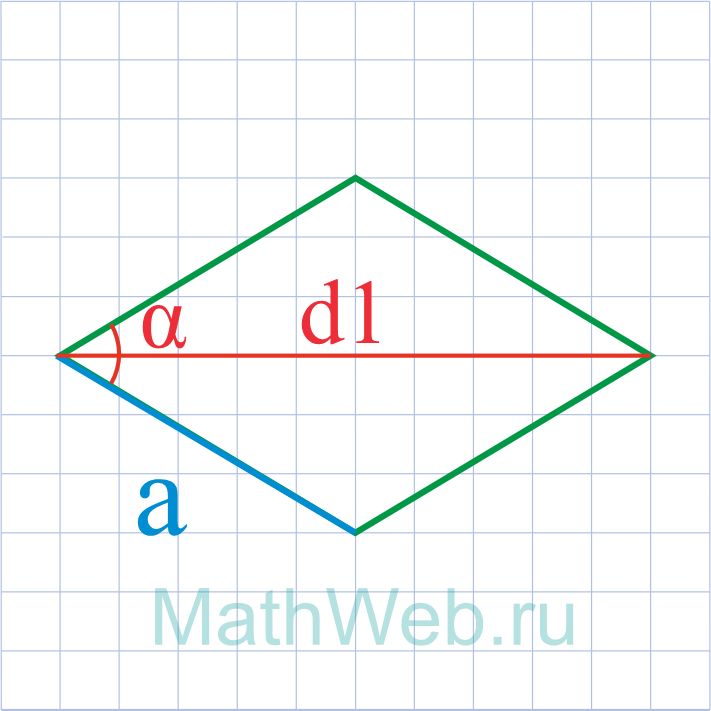Сторона ромба через длинную диагональ и острый угол.

a =

d1

√2 + 2·cos(α°)
Сторона ромба через короткую диагональ и тупой угол.

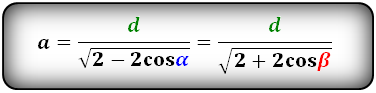
a =

d2

√2 – 2·cos(β°)
Сторона ромба через площадь и синус угла.

a =

√S

√sin(α°)

=

√S

√sin(β°)
Сторона ромба через площадь и радиус вписанной окружности.

a =

S

2r
Сторона ромба через периметр.

a =

P

4
Источник

Свойства ромба:

1. Ромб – частный случай параллелограмма

2. Противоположные стороны – параллельны

3. Все четыре стороны – равны

4. Диагонали пересекаются под прямым углом (90°)

5. Диагонали являются биссектрисами

сторона ромба

a – сторона ромба

D – большая диагональ

d – меньшая диагональ

α – острый угол

β – тупой угол

Формула стороны через диагонали, ( a ):

Формула стороны ромба

Формулы стороны через диагональ и угол, ( a ):

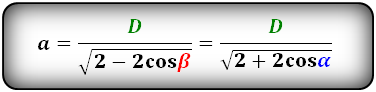
Формула стороны ромба

Формула стороны ромба

Формулы стороны через диагональ и половинный угол, ( a ):

Формула стороны ромба

Формула стороны ромба

Формулы стороны через диагонали и угол, ( a ):

Формула стороны ромба

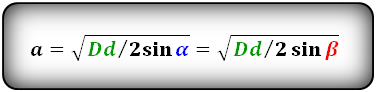
Формулы стороны через площадь ромба ( S ) и угол, ( a ):

Формула стороны ромба

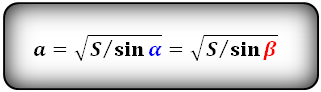
Формулы стороны через периметр ромба ( P ) и угол, ( a ):

Формула стороны ромба

Формулы площади ромба

Формула периметра ромба

Все формулы по геометрии

Подробности

Опубликовано: 27 ноября 2011

Обновлено: 13 августа 2021

Источник

Ромб – это параллелограмм с равными сторонами, поэтому вычислив любую его сторону, мы знаем все остальные. Диагонали ромба взаимно перпендикулярны, и образуют во внутреннем пространстве фигуры прямоугольные треугольники одинаковые по величине. Сторона ромба является гипотенузой в таком треугольнике, а половины диагоналей – катетами. Используя теорему Пифагора, подставим необходимые величины и найдем сторону ромба через диагонали:




Источник

Как найти сторону ромба по его диагоналям? Это можно сделать разными способами.

Kak nayti storonu romba po diagonalyam

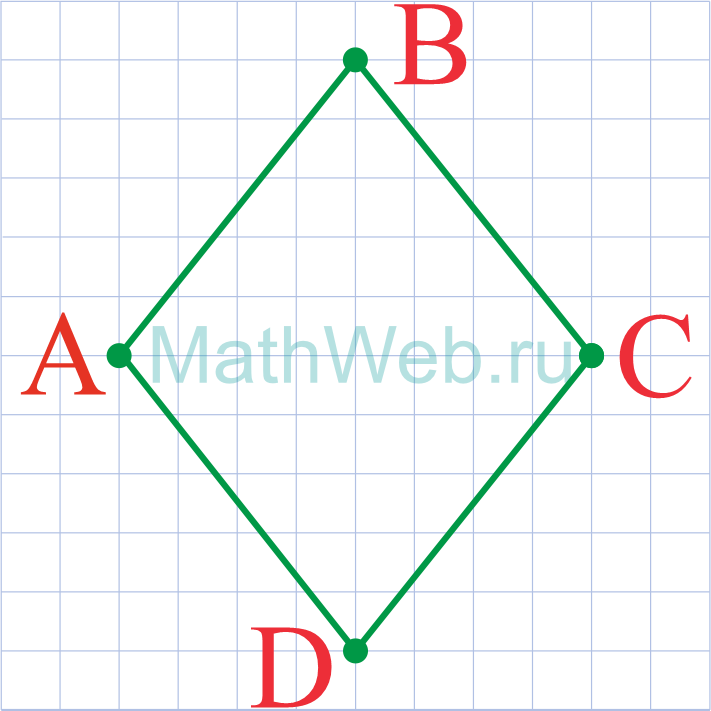
Дано:

ABCD — ромб,

    [AC = {d_1},]

    [BD = {d_2}.]

Найти:

AB.

Решение:

I способ

По свойствам ромба, его диагонали пересекаются под прямым углом и в точке пересечения делятся пополам.

storona romba po diagonalyam

Поэтому треугольник AOB — прямоугольный,

    [AO = frac{1}{2}AC = frac{1}{2}{d_1};]

    [BO = frac{1}{2}BD = frac{1}{2}{d_2}.]

По теореме Пифагора,

    [A{B^2} = A{O^2} + B{O^2}]

    [A{B^2} = {(frac{1}{2}{d_1})^2} + {(frac{1}{2}{d_2})^2}]

    [A{B^2} = frac{1}{4}(d_1^2 + d_2^2)]

    [underline {AB = frac{1}{2}sqrt {d_1^2 + d_2^2} } ]

Таким образом, сторона ромба равна половине квадратного корня из суммы квадратов его диагоналей:

    [underline {a = frac{1}{2}sqrt {d_1^2 + d_2^2} } ]

II способ.

Сумма квадратов диагоналей ромба равна сумме квадратов его сторон. Так как все стороны ромба равны, то

    [4A{B^2} = A{C^2} + B{D^2}]

    [A{B^2} = frac{1}{4}(A{C^2} + B{D^2})]

    [A{B^2} = frac{1}{4}(d_1^2 + d_2^2)]

    [underline {AB = frac{1}{2}sqrt {d_1^2 + d_2^2} } ]

Источник

Добавить комментарий