Так как в ромбе все четыре стороны равны, совсем несложно найти одну из них, если известен его периметр – просто делим на четыре.

И опять несложно определить одну из сторон, если известны площадь ромба и его высота:
нужно площадь разделить на высоту

Немножко сложнее, если известны диагонали – здесь без теоремы Пифагора и извлечением из под корня не обойтись:
сторона ромба равна половине корня квадратного от суммы квадратов диагоналей

Примечание:
на рисунке d1=D и d2=d
Также есть много других формул (более сложных), где сторону ромба можно найти через площадь и угол, через диагональ и угол и другие
Свойства ромба:
1. Ромб – частный случай параллелограмма
2. Противоположные стороны – параллельны
3. Все четыре стороны – равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формула стороны через диагонали, ( a ):
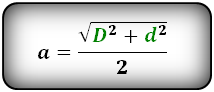
Формулы стороны через диагональ и угол, ( a ):
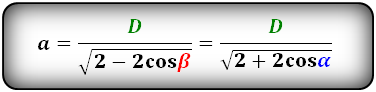
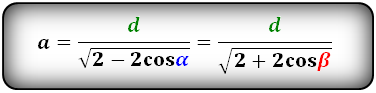
Формулы стороны через диагональ и половинный угол, ( a ):


Формулы стороны через диагонали и угол, ( a ):
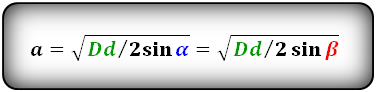
Формулы стороны через площадь ромба ( S ) и угол, ( a ):
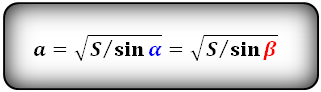
Формулы стороны через периметр ромба ( P ) и угол, ( a ):

Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 27 ноября 2011
-
Обновлено: 13 августа 2021
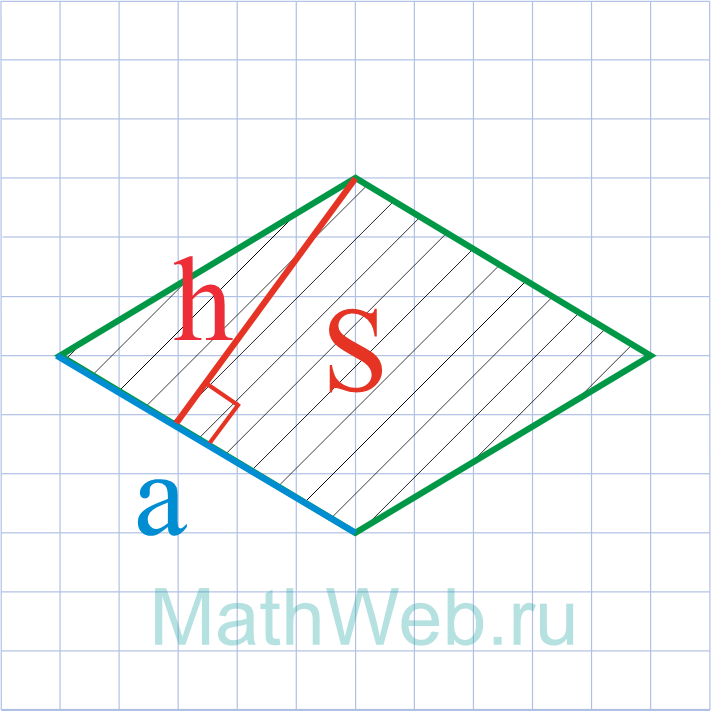
Где S – площадь ромба,h – его высота.
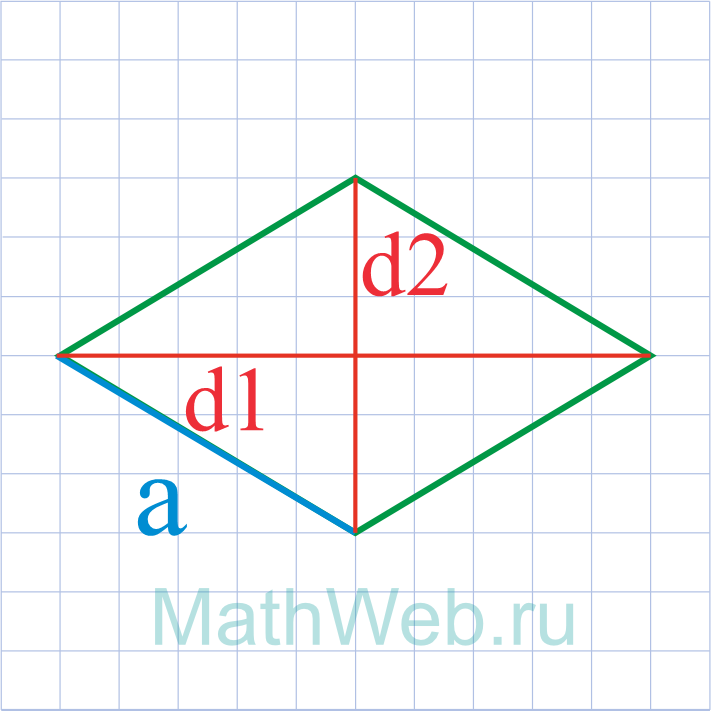
Где d1 – большая диагональ,d2 – меньшая диагональ.
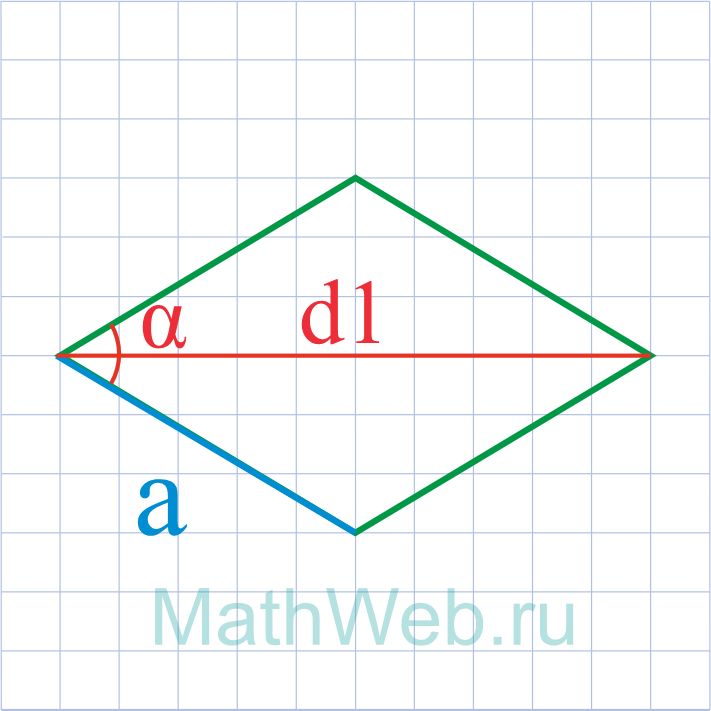
Где d1 – большая диагональ,α – острый угол.
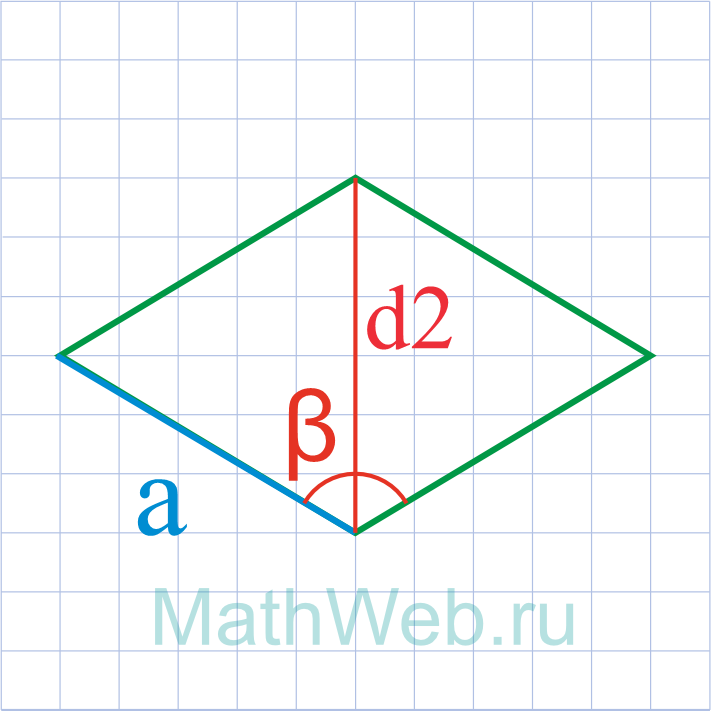
Где d2 – меньшая диагональ,β – тупой угол.
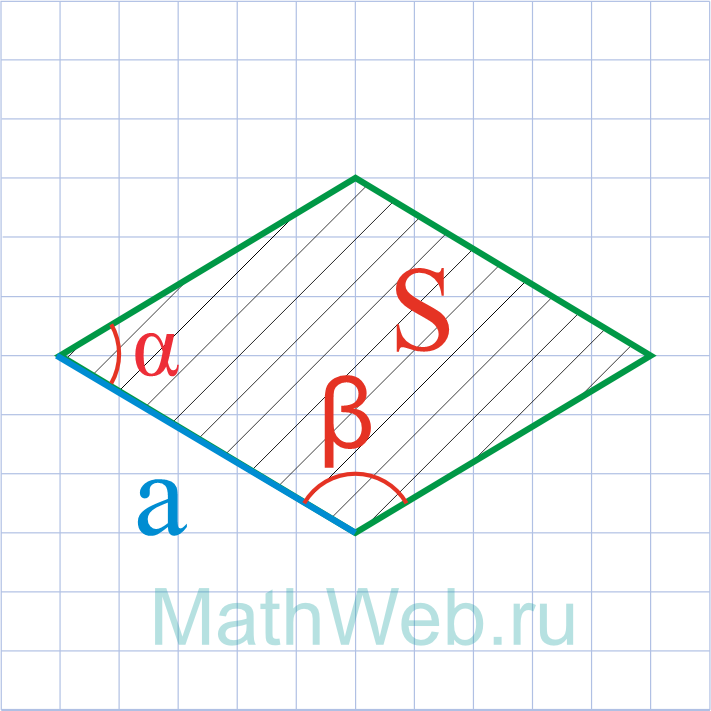
Где S – площадь ромба, α°,β° – его углы.
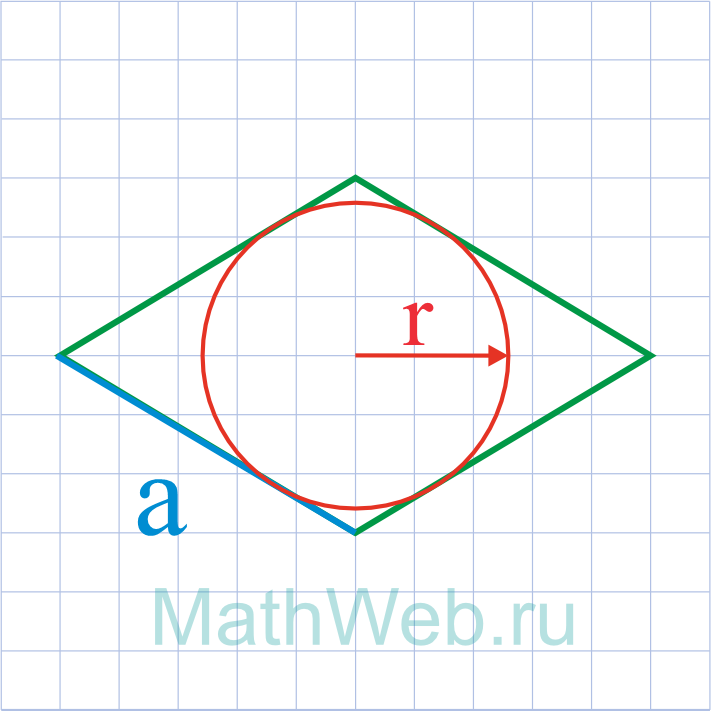
Где S – площадь ромба,r – радиус вписанной окружности.
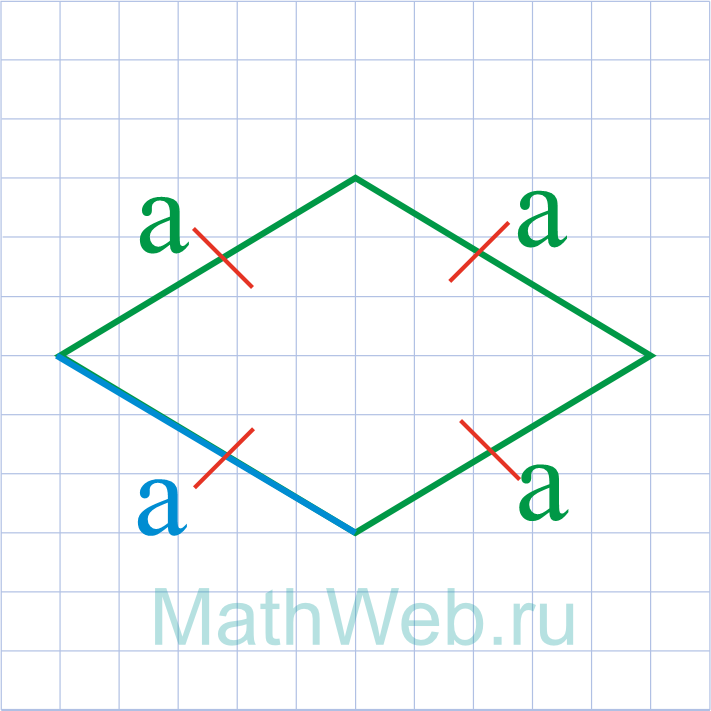
Где P – периметр ромба.
- Ромб – это параллелограмм у которого все стороны равны.
- Противоположные стороны ромба параллельны.
- Все ромбы различаются между собой только размером стороны и углов.
Как найти длину стороны ромба?
Сторона ромба может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = S h |
 |
a = √d12 ― d22 2 |
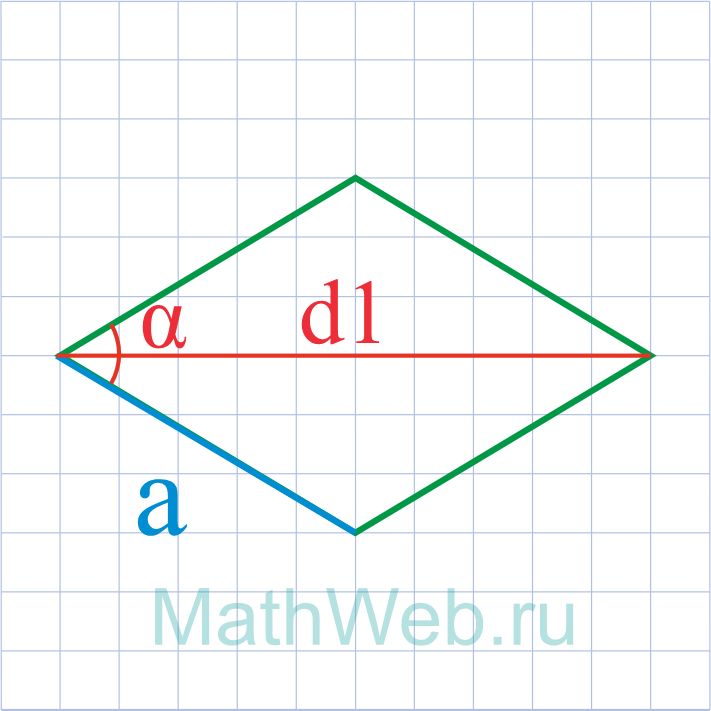 |
a = d1 √2 + 2·cos(α°) |
 |
a = d2 √2 – 2·cos(β°) |
 |
a = √S √sin(α°) = √S √sin(β°) |
 |
a = S 2r |
 |
a = P 4 |
Сторона ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Содержание
- Сторона ромба через высоту и площадь
- Сторона ромба через высоту и угол
- Сторона ромба через диагонали
- Сторона ромба через угол и противолежащую диагональ
- Сторона ромба через угол и диагональ из данного угла
- Сторона ромба через площадь и радиус вписанной в ромб окружности
- Сторона ромба через площадь и угол
1. Сторона ромба через высоту и площадь
Пусть известны площадь и высота ромба (Рис.1).
Покажем, что сторона ромба через высоту и площадь вычисляется формулой
Формула площади ромба через сторону и высоту имеет следующий вид:
Откуда легко вывести формулу (1).
2. Сторона ромба через высоту и угол
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
Для прямоугольного треугольника AHB применим теорему синусов:
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Сторона ромба через диагонали
Выведем формулу вычисления сторон ромба через диагонали.
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
Применим к прямоугольному треугольнику AOB теорему Пифагора:
Откуда:
4. Сторона ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
Подставляя (5) в (4), получим:
или
5. Сторона ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
Учитывая, что ( small BO=frac{large d}{large 2}) и ( small angle ABO=frac{large alpha}{large 2}), формулу (13) можно записать так:
или
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
Подставляя (9) в (8), получим:
или
6. Сторона ромба через площадь и радиус вписанной в ромб окружности
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
Из формулы (11) получим:
7. Сторона ромба через площадь и угол
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
Из формулы (13) найдем a:
Получили формулу сторон ромба через площадь и угол.
Ромб – это параллелограмм с равными сторонами, поэтому вычислив любую его сторону, мы знаем все остальные. Диагонали ромба взаимно перпендикулярны, и образуют во внутреннем пространстве фигуры прямоугольные треугольники одинаковые по величине. Сторона ромба является гипотенузой в таком треугольнике, а половины диагоналей – катетами. Используя теорему Пифагора, подставим необходимые величины и найдем сторону ромба через диагонали:




