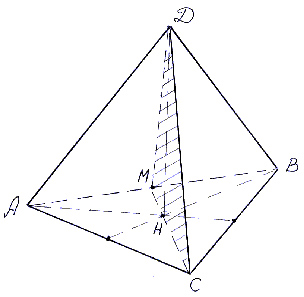
Как найти сечение параллелепипеда
Сечения геометрических фигур имеют различные формы. У параллелепипеда сечение всегда представляет собой прямоугольник или квадрат. Оно имеет ряд параметров, которые могут быть найдены аналитическим способом.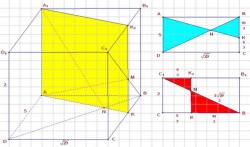
Через параллелепипед можно провести четыре сечения, которые представляют собой квадраты или прямоугольники. Всего он имеет два диагональных и два поперечных сечения. Как правило, они имеют разные размеры. Исключением является куб, у которого они одинаковы.
Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов – обычный и прямоугольный. У обычного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники или квадраты. Из этого следует,что куб – это частный случай прямоугольного параллелепипеда.
У любого сечения параллелепипеда есть определенные характеристики. Основными из них являются площадь, периметр, длины диагоналей. Если из условия задачи известны стороны сечения или какие-либо иные его параметры, этого достаточно, чтобы найти его периметр или площадь. По сторонам определяются также диагонали сечений. Первый из этих параметров – площадь диагонального сечения.
Для того чтобы найти площадь диагонального сечения, нужно знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ найдите по теореме Пифагора:
d=√a^2+b^2.
Найдя диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:
S=d*h.
Периметр диагонального сечения тоже можно вычислять по двум величинам – диагонали основания и высоте параллелепипеда. В этом случае вначале найдите две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а затем сложите с удвоенным значением высоты.
Если провести плоскость, параллельную ребрам параллелепипеда, можно получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения найдите следующим образом:
S=a*h.
Периметр этого сечения найдите аналогичным образом по следующей формуле:
p=2*(a+h).
Последний случай возникает, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:
S=a*b – площадь сечения;
p=2*(a+b).
Представь, что тебе в распоряжение дали накачанного мужика с бензопилой, 👷🏻♂️которой умеет ей владеть, и параллелепипеды из дерева, которые этот мужик может одним движением распилить, но мужик сильно ленивый, поэтому делает распил реально одним движением по плоскости. Так и получаются сечения прямоугольного параллелепипеда.
🔸 Вообще сечения параллелепипеда могут быть абсолютно любыми фигурами от треугольника до шестиугольника. Если отпилить уголок параллелепипеда по краю, на месте распила останется треугольник, а если выбрать самый сложный путь между дальними углами, то половинки останутся шестиугольниками. Но для ЕГЭ нам интереснее и полезнее всего будут четырехугольники в сечении.
💁🏻♂️ Самая простая идея распила — ровно пополам, тогда на отпиленной части у нас останется точно такой же прямоугольник, который был и слева и справа, Это самое приятное сечение называется параллельным граням параллелепипеда и равно той самой грани, которой оно параллельно, ну и противоположной ей тоже соответственно. Заметим приятную особенность такого сечения — оно симметрично относительно центра, если пилим строго пополам.
👇🏻 Если чуть заморочимся и будем пилить по диагонали параллелепипеда, но так, чтобы сечение было строго перпендикулярно основанию, то получим на оставшихся частях диагональное сечение. Это прямоугольник, у которого одна сторона равна боковой стороне параллелепипеда, а вторая сторона равна диагонали основания. Оба этих сечения встречаются в ЕГЭ чаще всего, поэтому знакомься и дружи с ними.
И будь аккуратнее с бензопилами! 💕

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Содержание
- Способы построения сечения параллелепипеда
- Методы построения сечений многогранников
- СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
- (система уроков и факультативных занятий по теме “Построение сечений многогранников”)
- Способы построения сечения параллелепипеда
- Способы построения сечения параллелепипеда
Способы построения сечения параллелепипеда
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Примеры построения сечений:
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA1D1D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.

Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.

Соединим точки K и M, лежащие в одной плоскости AA1B1B.

Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;

пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;

Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

MKNTPL — искомое сечение.
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.
 .
.
Соединим точки M и L, лежащие в плоскости AA1D1D.
 .
.
Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.
 .
.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
 .
.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
 .
.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
 .
.
Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).
 .
.
Соединим точки P и L ( они лежат в одной плоскости).
 .
.
Источник
Методы построения сечений многогранников
Разделы: Математика
Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.
Данный материал характеризуется следующим особенностями:
- Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
- В задачах используются в основном простейшие многогранники.
- Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.
Чтобы решить задачу построения сечения многогранника ученик должен знать:
- что значит построить сечение многогранника плоскостью;
- как могут располагаться относительно друг друга многогранник и плоскость;
- как задается плоскость;
- когда задача на построение сечения многогранника плоскостью считается решенной.
Поскольку плоскость определяется:
- тремя точками;
- прямой и точкой;
- двумя параллельными прямыми;
- двумя пересекающимися прямыми,
построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.
Существует три основных метода построения сечений многогранников:
- Метод следов.
- Метод вспомогательных сечений.
- Комбинированный метод.
Первые два метода являются разновидностями Аксиоматического метода построения сечений.
Можно также выделить следующие методы построения сечений многогранников:
- построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
- построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
- построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
- построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
- построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.
В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:
- Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
- Погорелова А.В. (Геометрия, 7-11);
- Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
- Смирновой И.М. (Геометрия, 10-11);
- Шарыгина И.Ф. (Геометрия, 10-11).
Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.
В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).
В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.
Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.
Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:
- Определение сечения многогранников.
- Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
- Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
- Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
(система уроков и факультативных занятий по теме “Построение сечений многогранников”)
Тема урока: “Построение сечений многогранников”.
Цель урока: ознакомление с методами построений сечений многогранников.
Источник
Способы построения сечения параллелепипеда
Задача №1: Построить сечение ( PQR ) параллелепипеда. Все точки лежат на ребрах двух смежных граней.

1) Так как точки P и Q лежат в плоскости грани A ‘ B ‘ BA , соединим эти точки. Прямая PQ пересекает ребра BA и BB’ в точках F и G соответственно ;
2) Так как точки Q и R лежат в плоскости грани A ‘ B ‘ C ‘ D ‘, соединим эти точки;
3) Так как точки G и R лежат в плоскости грани BCC ‘ B ‘, соединим эти точки. Прямая GR пересекает ребра CC ‘ и BC в точках H и M соответственно;
4) Так как точки F и M лежат в плоскости грани ABCD , соединим эти точки. Прямая FM пересекает ребра AD и DC в точках N и K соответственно;
Соединим последовательно точки P, Q, R, H, K, N. Получим искомое сечение PQRHKN.


Задача №2 : Построить сечение параллелепипеда ( MLK ). Точки K и L лежат на ребрах нижнего основания AB и CB соответственно, а точка М принадлежит боковому ребру DD’ .

1) Так как точки K и L лежат в плоскости грани A ‘ B ‘ C ‘ D ‘, соединим эти точки. Прямая KL пересекает ребра DC и AD в точках X1 и X2;
2) Так как точки M и X1 лежат в плоскости грани CDD ‘ C ‘, соединим эти точки. Прямая MX1 пересекает ребро CC’ в точке Y;
3) Так как точки M и X2 лежат в плоскости грани ADD ‘ A ‘, соединим эти точки. Прямая MX2 пересекает ребро AA’ в точке P;
4) Соединим последовательно точки L, Y, M, P, K. Получим искомое сечение LYMPK.
Источник
Способы построения сечения параллелепипеда

Строим сечение параллелепипеда по трем точкам (М, Р и N), лежащим на трех соседних ребрах.
Построение:
1. Отрезок MN. Так как М и Р лежат на нижней грани
2. Отрезок NР. Так как Р и N лежат на боковой грани
3. Отрезок MР. Так как эти точки тоже лежат в одной плоскости
4. Δ MNР – искомое сечение

Строим сечение параллелепипеда по трем точкам (М, Р и N), лежащим на трех параллельных ребрах.
Построение:
1. Отрезок MN
2. Отрезок NР
3. РQ II MN
4. PQ ∩ DD1 = Q
5. MQ II NP
6. MNРQ – искомое сечение

Строим сечение параллелепипеда по трем точкам (М, Р и N), не лежащим на трех параллельных ребрах
Построение:
1. Отрезок MN
2. Отрезок NР
3. РQ II MN
4. PQ ∩ А1В1 = Q
5. Отрезок MQ
6. MNРQ – искомое сечение
Перейдем к построению более сложных сечений

Строим сечение параллелепипеда по трем точкам (М, Р и N), не лежащим на трех параллельных ребрах. Пользуемся методом следов.
Построение:
1. Отрезок MN
2. Прямая NР
3. NP ∩ CD = K
4. MK ∩ AB = S
5. MS ∩ AD = L
6. PN ∩ DD1 = E
7. Прямая LE
8. LE ∩ AA1 = R
9. LE ∩ A1D1 = Q
10. MNРQRS – искомое сечение
2. Построение сечений в тетраэдре
2.1. Построение сечения в тетраэдре по трем точкам (М, Р и N)

Построение:
1. Отрезок NР
2. Отрезок MР
3. Отрезок MN
4. Δ MNР – искомое сечение
2.2. Построение по трем точкам (М, Р и N)

Построение:
1. Отрезок MN
2. Отрезок NР
3. Отрезок MР
4. Δ MNР – искомое сечение
2.3. Построение по трем точкам (М, Р и N)

Построение:
1. Отрезок NР
2. Прямая MN
3. MN ∩ АВ = К
4. Прямая КP
5. КР ∩ АС = Q
6. Отрезок MQ
7. MNРQ – искомое сечение
2.4. Построение по трем точкам (М, Р и N)
Источник
Параллелепипед. Построение сечений параллелепипеда
План урока
- Параллелепипед;
- Построение сечений параллелепипеда.
Цели урока
- Знать, что такое параллелепипед и как называются его элементы;
- Знать, что понимают под сечением параллелепипеда;
- Уметь строить сечения параллелепипеда.
Разминка
- Что такое параллелограмм?
- Какие плоскости называются параллельными?
- Что такое тетраэдр?
- Какие геометрические фигуры могут являться сечением тетраэдра?
Параллелепипед
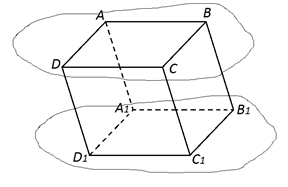
Рис. 1
Пусть два равных параллелограмма ABCDи A1B1C1D1 лежат в параллельных плоскостях и расположены так, что отрезки AA1, BB1, CC1, DD1 параллельны (рис. 1.).
Как известно, если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны (свойство параллельных плоскостей). Отсюда следует, что параллельными будут следующие пары отрезков: AB и A1B1, CD и C1D1, BC и B1C1, AD и A1D1.
Тогда каждый из четырёхугольников ABB1A1, BCC1B1, CDD1C1, DAA1D1 имеет попарно параллельные противоположные стороны, т.е. является параллелограммом. Пространственная фигура, составленная из параллелограммов ABCD, A1B1C1D1, ABB1A1, BCC1B1, CDC1D1, DAA1D1 называется параллелепипедом и обозначается ABCDA1B1C1D1.
Параллелепипед, как и тетраэдр, является разновидностью многогранников, которым будет посвящена одна из глав курса стереометрии.
Параллелепипед
– поверхность, составленная из шести параллелограммов.
Параллелограммы, из которых составлен параллелепипед, называются
гранями
параллелепипеда.
Параллелепипед, у которого все грани – прямоугольники, называется
прямоугольным параллелепипедом
.
Стороны этих параллелограммов называются рёбрами параллелепипеда.
Вершины этих параллелограммов называются вершинами параллелепипеда.
Две вершины параллелепипеда, не лежащие в одной грани, называются противоположными.
Отрезок, соединяющий противоположные вершины параллелепипеда, называется диагональю.
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер – противоположными.
На рисунке 1 противоположными являются грани ABCD и A1B1C1D1, AA1D1D и BB1C1C, ABB1A1 и DCC1D1. В параллелепипеде ABCDA1B1C1D1 можно провести диагонали AC1, A1C, DB1, D1B.
Две какие-нибудь противоположные грани параллелепипеда можно рассматривать как основания. Тогда все другие грани называют боковыми.
Рёбра параллелепипеда, не принадлежащие основанию, также называют боковыми.
Сформулируем и докажем два свойства параллелепипеда.
Свойство 1
Противоположные грани параллелепипеда параллельны и равны.
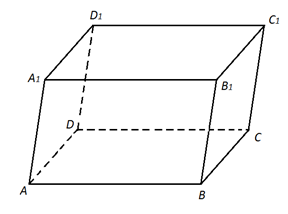
Рис. 2.
Две грани параллелепипеда называются
параллельными
, если их плоскости параллельны.
Докажем параллельность и равенство граней ABB1A1 и DCC1D1 параллелепипеда ABCDA1B1C1D1 (рис. 2).
Из определения параллелепипеда следует, что все его грани – параллелограммы. Из того, что ABCD и ADD1A1 – параллелограммы, следует, что AB∥DC и AA1∥DD1. Таким образом, две пересекающиеся прямые (AB и AA1) одной грани соответственно параллельны двум прямым (CD и DD1) другой грани. Следовательно, по признаку параллельности плоскостей, грани ABB1A1 и DCC1D1 параллельны.
Стороны углов A1AB и D1DC сонаправлены, а значит эти углы равны.
Так как противоположные стороны параллелограмма равны, то AB=DC, AA1=DD1.
Итак, две смежные стороны и угол между ними параллелограмма ABB1A1 соответственно равны двум смежным сторонам и углу между ними параллелограмма DCC1D1. Значит, эти параллелограммы равны.
Свойство 2
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
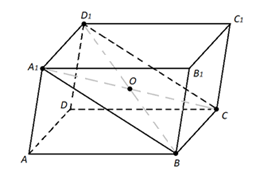
Рис. 3
Рассмотрим четырёхугольник A1D1CB (рис. 3). Диагонали этого четырёхугольника (A1C и D1B) являются диагоналями параллелепипеда ABCDA1B1C1D1 (рис. 3).
A1D1∥BC и A1D1=BC, значит A1D1CB – параллелограмм. Из свойств параллелограмма следует, что диагонали пересекаются в некоторой точке O и в этой точке делятся пополам.
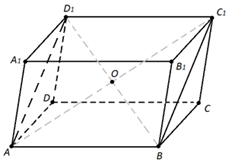
Рис. 4
Рассмотрим теперь четырёхугольник AD1C1B (рис. 4). Он также является параллелограммом (доказывается аналогично). Значит его диагонали AC1 и D1B пересекаются и точкой пересечения делятся пополам. При этом серединой диагонали D1B является точка O. Значит и серединой диагонали AC1 является точка O.

Рис. 5
В четырёхугольнике A1B1CD аналогично доказывается, что и диагональ DB1 проходит через точку O и делится в ней пополам (рис. 5).
Таким образом, все четыре диагонали параллелепипеда пересекаются в одной точке и делятся в этой точке пополам.
Упражнение 1
Изобразите параллелепипед MNKLM1N1K1L1. Запишите:
а) рёбра параллелепипеда;
б) грани параллелепипеда;
в) диагонали параллелепипеда;
г) пары противоположных граней.
Построение сечений параллелепипеда
Дадим определения, аналогичные тем, что рассматривались при изучении тетраэдра и его сечений.
Секущая плоскость параллелепипеда
– это плоскость, по обе стороны от которой имеются точки данного параллелепипеда.
Секущая плоскость параллелепипеда пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки представляет собой сечение параллелепипеда.
Сечение параллелепипеда
– многоугольник, образованный пересечением плоскости с данным параллелепипедом.
Параллелепипед имеет шесть граней, значит сечение параллелепипеда не может иметь более шести сторон. Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.
Рассмотрим примеры построения различных сечений параллелепипеда.
Пример 1
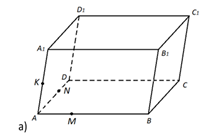
Рис. 6.
На рёбрах AB, AD, AA1 параллелепипеда ABCDA1B1C1D1 отмечены точки M, N и K так, как показано на рисунке 6. Построить сечение параллелепипеда плоскостью MNK.
Решение
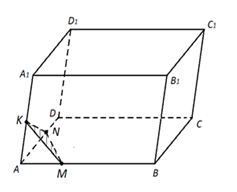
Рис. 7.
На рисунке 6 изображён исходный параллелепипед и точки M, N и K. Плоскость MNK пересекает грани параллелепипеда по отрезкам MN, NK и MK. В совокупности они представляет собой треугольник MNK, который и является сечением данного параллелепипеда (рис. 7).
Пример 2
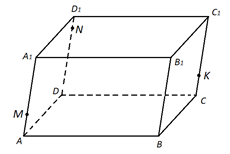
Рис. 8.
На рёбрах AA1, DD1, CC1 параллелепипеда ABCDA1B1C1D1 отмечены точки M, N и K так, как показано на рисунке 8. Построить сечение параллелепипеда плоскостью MNK.
Решение
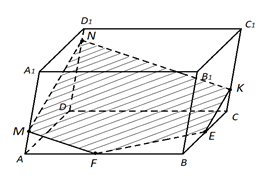
Рис. 9.
Проведём сначала отрезки MN и NK.
Проведём через точку M прямую, параллельную NK и отметим точку пересечения этой прямой с ребром AB. Обозначим эту точку буквой F.
Через точку K проведём прямую параллельную MN и отметим точку пересечения этой прямой с ребром BC. Обозначим эту точку буквой E. Проведём отрезок EF. Многоугольник MNKEF – искомое сечение.
Пример 3
На рёбрах AA1, A1D1, D1C1 параллелепипеда ABCDA1B1C1D1 отмечены точки M, N и K так как показано на рисунке 10а. Построить сечение параллелепипеда плоскостью MNK.
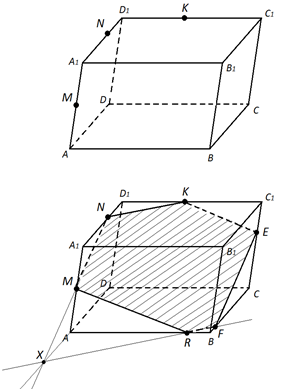
Рис. 10 (а, б).
Построим отрезки MNи NK (рис. 10б).
Далее проведём прямые MN и DA.
Отметим точку пересечения этих прямых и обозначим её буквой X.
Через точку X проведём прямую, параллельную NK.
Отметим точки пересечения этой прямой с рёбрами AB и BC.
Обозначим их соответственно R и F.
Через точку F проведём прямую, параллельную MN.
Отметим точку пересечения этой прямой с ребром CC1.
Обозначим эту точку буквой E.
Многоугольник MNKEFR – искомое сечение.
Упражнение 2
1. Может ли сечением параллелепипеда быть:
а) четырёхугольник;
б) пятиугольник;
в) шестиугольник;
г) семиугольник.
2. Дан параллелепипед ABCDA1B1C1D1. Сумма всех его рёбер равна 120 см. Найдите каждое ребро параллелепипеда, если
ABBC=45, BCBB1=56.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью ABC1.
4. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку M грани AA1B1B. Постройте сечение параллелепипеда плоскостью, проходящей через точку M параллельно плоскости ABCD.
Контрольные вопросы
1. Какая геометрическая фигура называется параллелепипедом?
2. Что представляет собой сечение параллелепипеда?
3. Какие геометрические фигуры могут являться сечением параллелепипеда?
Ответы
Упражнение 2
- а) да; б) да; в) да; г) нет.
- 8 см, 10 см, 12 см.
- рис. 11.
- рис. 12.
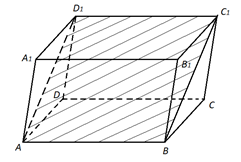
Рис. 11.
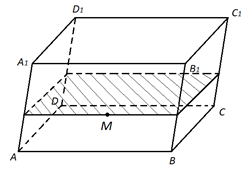
Рис. 12.
Метод сечений многогранников в стереометрии
используется в задачах на построение. В его
основе лежит умение строить сечение
многогранника и определять вид сечения.
Данный материал характеризуется следующим
особенностями:
- Метод сечений применяется только для
многогранников, так как различные сложные
(наклонные) виды сечений тел вращения не входят в
программу средней школы. - В задачах используются в основном простейшие
многогранники. - Задачи представлены в основном без числовых
данных, чтобы создать возможность их
многовариантного использования.
Чтобы решить задачу построения сечения
многогранника ученик должен знать:
- что значит построить сечение многогранника
плоскостью; - как могут располагаться относительно друг
друга многогранник и плоскость; - как задается плоскость;
- когда задача на построение сечения
многогранника плоскостью считается решенной.
Поскольку плоскость определяется:
- тремя точками;
- прямой и точкой;
- двумя параллельными прямыми;
- двумя пересекающимися прямыми,
построение плоскости сечения проходит в
зависимости от задания этой плоскости. Поэтому
все способы построения сечений многогранников
можно разделить на методы.
Существует три основных метода построения
сечений многогранников:
- Метод следов.
- Метод вспомогательных сечений.
- Комбинированный метод.
Первые два метода являются разновидностями Аксиоматического
метода построения сечений.
Можно также выделить следующие методы
построения сечений многогранников:
- построение сечения многогранника плоскостью,
проходящей через заданную точку параллельно
заданной плоскости; - построение сечения, проходящего через заданную
прямую параллельно другой заданной прямой; - построение сечения, проходящего через заданную
точку параллельно двум заданным скрещивающимся
прямым; - построение сечения многогранника плоскостью,
проходящей через заданную прямую
перпендикулярно заданной плоскости; - построение сечения многогранника плоскостью,
проходящей через заданную точку перпендикулярно
заданной прямой.
В федеральный перечень учебников по геометрии
для 10-11 класов входят учебники авторов:
- Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др
(Геометрия, 10-11); - Погорелова А.В. (Геометрия, 7-11);
- Александрова А.Д., Вернера А.Л., Рыжик В.И.
(Геометрия, 10-11); - Смирновой И.М. (Геометрия, 10-11);
- Шарыгина И.Ф. (Геометрия, 10-11).
Рассмотрим подробнее учебники Л.С, Атанасяна и
Погорелова А.В.
В учебнике Л.С. Атанасяна на тему “Построение
сечений многогранников” выделено два часа. В 10
классе в теме “Параллельность прямых и
плоскостей” после изучения тетраэдра и
параллелепипеда отводится один час на изложение
параграфа “Задачи на построение сечений”.
Рассматриваются сечения тетраэдра и
параллелепипеда. И тема “Параллельность прямых
и плоскостей” завершается решением задач на
одном или двух часах (всего задач на построение
сечений в учебнике восемь).
В учебнике Погорелова А.В. на построение
сечений отводится около трех часов в главе
“Многогранники”: один – на изучение темы
“Изображение призмы и построение ее сечений”,
второй – на изучение темы “Построение пирамиды
и ее плоских сечений” и третий – на решение
задач. В списке задач, приведенных после темы,
задач на сечение насчитывается всего около
десяти.
Мы предлагаем систему уроков по теме
“Построение сечений многогранников” для
учебника Погорелова А.В.
Материал предлагается расположить в той
последовательности, в какой он может применяться
для обучения учащихся. Из изложения темы
“Многогранники” предлагается исключить
следующие параграфы: “Построение сечений
призмы” и “Построение сечений пирамиды” с тем,
чтобы систематизировать данный материал в конце
этой темы “Многогранники”. Классифицировать
его по тематике задач с примерным соблюдением
принципа “от простого к сложному” можно весьма
условно следующим образом:
- Определение сечения многогранников.
- Построение сечений призмы, параллелепипеда,
пирамиды методом следов. (Как правило в школьном
курсе стереометрии используются задачи на
построение сечений многогранников, решаемые
основными методами. Остальные методы, в связи с
их более высоким уровнем сложности, учитель
может оставить для рассмотрения на
факультативных занятиях или на самостоятельное
изучение. В задачах на построение основными
методами требуется построить плоскость сечения,
проходящую через три точки). - Нахождение площади сечений в многогранниках
(без использования теоремы о площади
ортогональной проекции многоугольника). - Нахождение площади сечений в многогранниках (с
применением теоремы о площади ортогональной
проекции многоугольника).
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА
ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ
ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.(система уроков и факультативных
занятий по теме “Построение сечений
многогранников”)
УРОК 1.
Тема урока: “Построение сечений
многогранников”.
Цель урока: ознакомление с методами
построений сечений многогранников.
Этапы урока:
- Актуализация опорных знаний.
- Постановка задачи.
- Изучение нового материала:
А) Определение сечения.
Б) Методы построений сечений:
а) метод следов;
б) метод вспомогательных сечений;
в) комбинированный метод.
- Закрепление материала.
Примеры построений сечений методом следов.
- Подведение итогов урока.
Тест.
Ход урока.
- Актуализация опорных знаний.
- Постановка задачи.
- Изучение нового материала.
Вспомним:
– пересечение прямой с плоскостью;
– пересечение плоскостей;
– свойства параллельных плоскостей.
Вопросы к классу:
– Что значит построить сечение многогранника
плоскостью?
– Как могут располагаться относительно друг
друга многогранник и плоскость?
– Как задается плоскость?
– Когда задача на построение сечения
многогранника плоскостью считается решенной?
А) Итак, задача состоит в построении
пересечения двух фигур: многогранника и
плоскости ( рис.1). Это могут быть: пустая фигура
(а), точка (б), отрезок (в), многоугольник (г). Если
пересечение многогранника и плоскости есть
многоугольник, то этот многоугольник называется сечением
многогранника плоскостью.
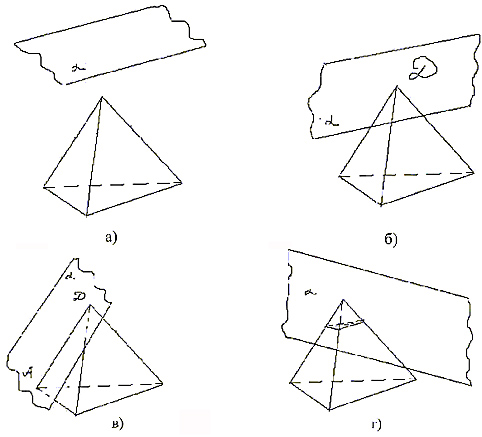
Рис. 1
Будем рассматривать только случай, когда
плоскость пересекает многогранник по его
внутренности. При этом пересечением данной
плоскости с каждой гранью многогранника будет
некоторый отрезок. Таким образом, задача
считается решенной, если найдены все отрезки, по
которым плоскость пересекает грани
многогранника.
Исследуйте сечения куба (рис.2) и ответьте на
следующие вопросы:
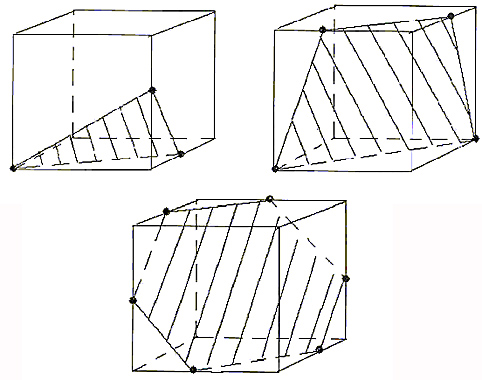
Рис. 2
– какие многоугольники получаются в сечении
куба плоскостью? (Важно число сторон
многоугольника);
[ Предполагаемые ответы: треугольник,
четырехугольник, пятиугольник, шестиугольник.]
– может ли в сечении куба плоскостью получиться
семиугольник? А восьмиугольник и т.д.? Почему?
Давайте рассмотрим призму и ее возможные
сечения плоскостью ( на модели). Какие
многоугольники получаются?
Какой можно сделать вывод? Чему равно
наибольшее число сторон многоугольника,
полученного сечением многогранника с
плоскостью?
[ Наибольшее число сторон многоугольника,
полученного в сечении многогранника плоскостью,
равно числу граней многогранника.]
Б) а) Метод следов заключается в построении
следов секущей плоскости на плоскость каждой
грани многогранника. Построение сечения
многогранника методом следов обычно начинают с
построения так называемого основного следа
секущей плоскости, т.е. следа секущей плоскости
на плоскости основания многогранника.
б) Метод вспомогательных сечений
построения сечений многогранников является в
достаточной мере универсальным. В тех случаях,
когда нужный след (или следы) секущей плоскости
оказывается за пределами чертежа, этот метод
имеет даже определенные преимущества. Вместе с
тем следует иметь ввиду, что построения,
выполняемые при использовании этого метода,
зачастую получаются “скученными”. Тем не менее
в некоторых случаях метод вспомогательных
сечений оказывается наиболее рациональным.
Метод следов и метод вспомогательных сечений
являются разновидностями аксиоматического
метода построения сечений многогранников
плоскостью.
в) Суть комбинированного метода построения
сечений многогранников состоит в применении
теорем о параллельности прямых и плоскостей в
пространстве в сочетании с аксиоматическим
методом.
А теперь на примере решения задач рассмотрим метод
следов.
4. Закрепление материала.
Задача 1.
Построить сечение призмы ABCDA1B1C1D1
плоскостью, проходящей через точки P, Q, R (точки
указаны на чертеже (рис.3)).
Решение.
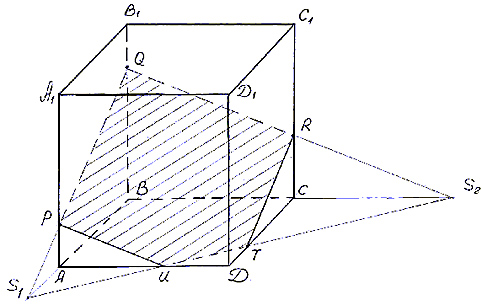
Рис. 3
- Построим след секущей плоскости на плоскость
нижнего основания призмы. Рассмотрим грань АА1В1В.
В этой грани лежат точки сечения P и Q. Проведем
прямую PQ. - Продолжим прямую PQ, которая принадлежит
сечению, до пересечения с прямой АВ. Получим
точку S1, принадлежащую следу. - Аналогично получаем точку S2 пересечением
прямых QR и BC. - Прямая S1S2 – след секущей плоскости
на плоскость нижнего основания призмы. - Прямая S1S2 пересекает сторону AD в
точке U, сторону CD в точке Т. Соединим точки P и U,
так как они лежат в одной плоскости грани АА1D1D.
Аналогично получаем TU и RT. - PQRTU – искомое сечение.
Задача 2.
Построить сечение параллелепипеда ABCDA1B1C1D1
плоскостью, проходящей через точки M, N, P (точки
указаны на чертеже (рис.4)).
Решение.
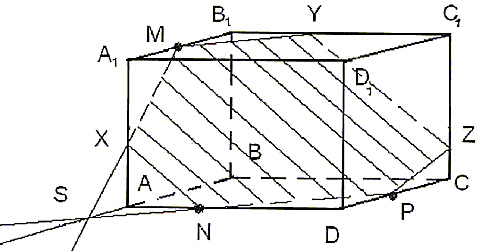
Рис. 4
- Точки N и P лежат в плоскости сечения и в
плоскости нижнего основания параллелепипеда.
Построим прямую, проодящую через эти точки. Эта
прямая является следом секущей плоскости на
плоскость основания параллелепипеда. - Продолжим прямую, на которой лежит сторона AB
параллелепипеда. Прямые AB и NP пересекутся в
некоторой точке S. Эта точка принадлежит
плоскости сечения. - Так как точка M также принадлежит плоскости
сечения и пересекает прямую АА1 в некоторой
точке Х. - Точки X и N лежат в одной плоскости грани АА1D1D,
соединим их и получим прямую XN. - Так как плоскости граней параллелепипеда
параллельны, то через точку M можно провести
прямую в грани A1B1C1D1,
параллельную прямой NP. Эта прямая пересечет
сторону В1С1 в точке Y. - Аналогично проводим прямую YZ, параллельно
прямой XN. Соединяем Z с P и получаем искомое
сечение – MYZPNX.
Задача 3 ( для самостоятельного
решения).
Построить сечение тетраэдра DACB плоскостью,
проходящей через точки M, N, P (точки указаны на
чертеже (рис.5)).
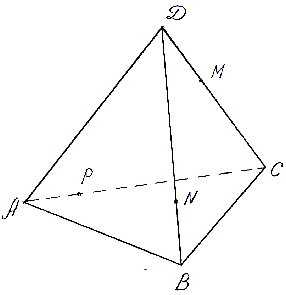
Рис. 5
5. Подведение итогов урока.
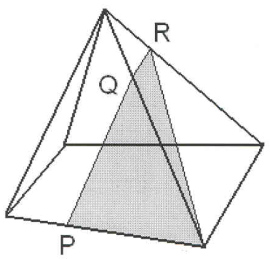
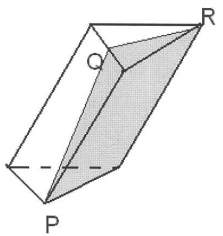
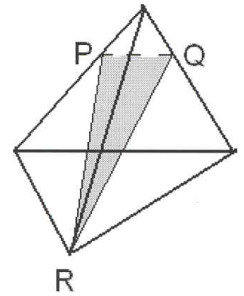
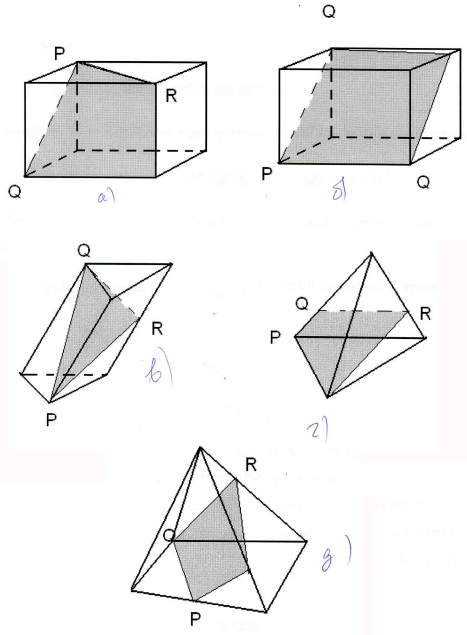
Ответьте на вопрос: являются ли закрашенные
фигуры сечениями изображенных многогранников
плоскостью PQR? И выполните правильное построение
(рис. 6).
Вариант 1.
а)
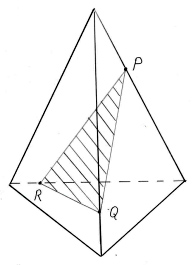
б)
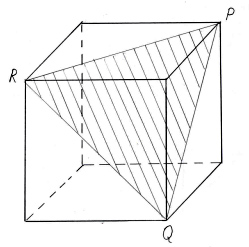
в)
г)
д)
Вариант 2.
УРОК 2.
Тема урока: НАХОЖДЕНИЕ ПЛОЩАДИ СЕЧЕНИЯ.
Цель урока: познакомить со способами
нахождения площади сечения многогранника.
Этапы урока:
- Актуализация опорных знаний.
- Решение задач на нахождение площади сечения:
Вспомнить теорему о площади ортогональной
проекции многоугольника.
– без использования теоремы о площади
ортогональной проекции многоугольника;
– с использованием теоремы о площади
ортогональной проекции многоугольника.
3. Подведение итогов урока.
Ход урока.
- Актуализация опорных знаний.
- Решение задач.
Вспомним теорему о площади ортогональной
проекции многоугольника: площадь
ортогональной проекции многоугольника на
плоскость равна произведению его площади на
косинус угла между плоскостью многоугольника и
плоскостью проекции.
Задача 1.
ABCD – правильная треугольная пирамида со
стороной основания AB равной а и высотой DH
равной h. Постройте сечение пирамиды
плоскостью, проходящей через точки D, C и М, где М –
середина стороны АВ, и найдите его площадь (рис.7).
Решение.
Сечением пирамиды является треугольник MCD.
Найдем его площадь.
- Так как основание пирамиды – равносторонний
треугольник и точка М – середина стороны, то СМ
является высотой и тогда, СМ =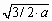 .
. - Площадь треугольника можно найти:
S = 1/2 · DH · CM = 1/2 ·
=
Рис.7
Задача 2.
Найти площадь сечения куба ABCDA1B1C1D1
с ребром а плоскостью, проходящей через
вершину D и точки Е и F на ребрах А1D1 и C1D1
соответственно, если A1E = k · D1E и C1F
= k · D1F.
Решение.
Построение сечения:
- Поскольку точки Е и F принадлежат плоскости
сечения и плоскости грани A1B1C1D1,
а две плоскости пересекаются по прямой, то прямая
EF будет являться следом секущей плоскости на
плоскость грани A1B1C1D1
(рис.8). - Аналогично получаются прямые ED и FD.
- EDF – искомое сечение.
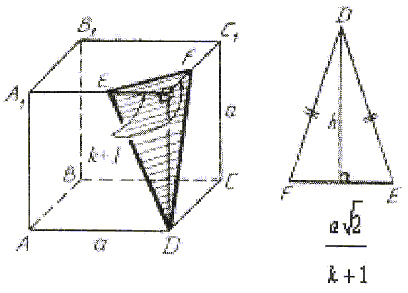
Рис.8.

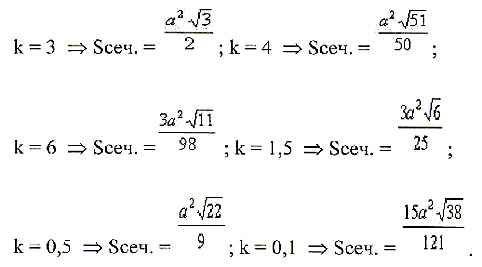
Задача 3 (для самостоятельного решения).
Построить сечение куба ABCDA1B1C1D1
со стороной а плоскостью, проходящей через
точки B, M и N, где Ь – середина ребра АА1, а N –
середина ребра СС1.
Решение.
Сечение строим методом следов.
Площадь сечения находим с помощью теоремы о
площади ортогональной проекции многоугольника.
Ответ: S = 1/2 · a2![]() .
.