Как найти сторону сечения пирамиды

Как найти сторону основания пирамиды

Задачи на вычисление стороны основания пирамиды составляют в задачнике по геометрии довольно большой раздел. Очень многое зависит от того, какая гемоетрическая фигура лежит в основании, а также от того, что дано в условиях задачи.

Вам понадобится

• – чертежные принадлежности;
• – тетрадь в клетку;
• – теорема синусов;
• – теорема Пифагора;
• – калькулятор.

Инструкция

В школьном курсе геометрии рассматриваются главным образом пирамиды, в основании которых лежит правильный многоугольник, то есть такой, у которого все стороны равны. Проекция вершины пирамиды совпадает с центром ее основания. Начертите пирамиду, в основании которой лежит равносторонний треугольник. В условиях могут быть даны:
– длина бокового ребра пирамиды и угол его с ребром между боковой гранью и основанием;
– длина бокового ребра и высота боковой грани;
– длина бокового ребра и высота пирамиды.

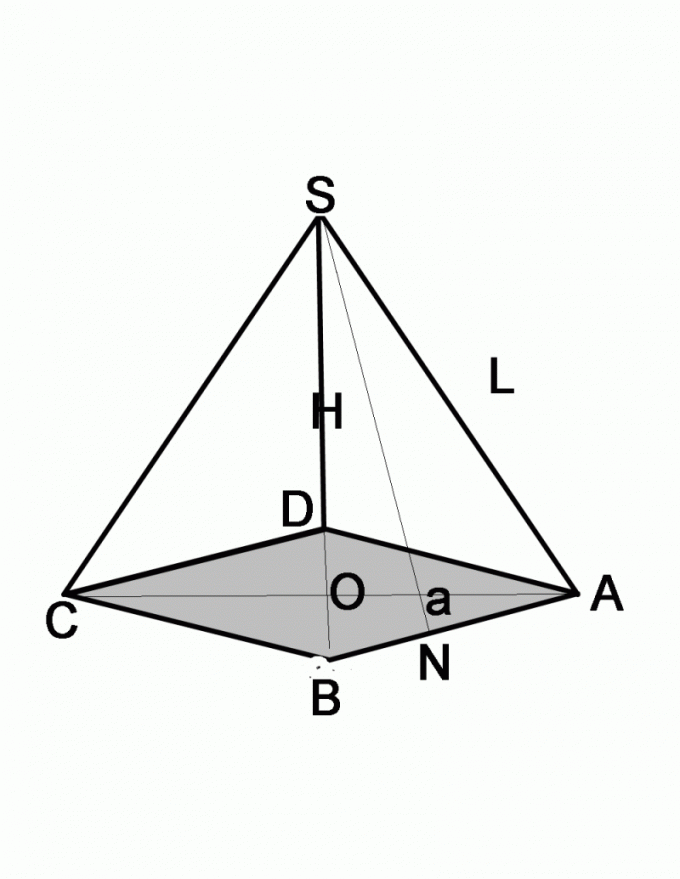
Если известны боковое ребро и угол, задача решается несколько иначе. Вспомните, что собой представляет каждая боковая грань пирамиды, в основании которой лежит равносторонний многоугольник. Это равнобедренный треугольник. Проведите его высоту, которая одновременно является биссектрисой и медианой. То есть половина стороны основания a/2=L*cosA, где а – сторона основания пирамиды, L – длина ребра. Чтобы найти размер стороны основания, достаточно полученный результат умножить на 2.

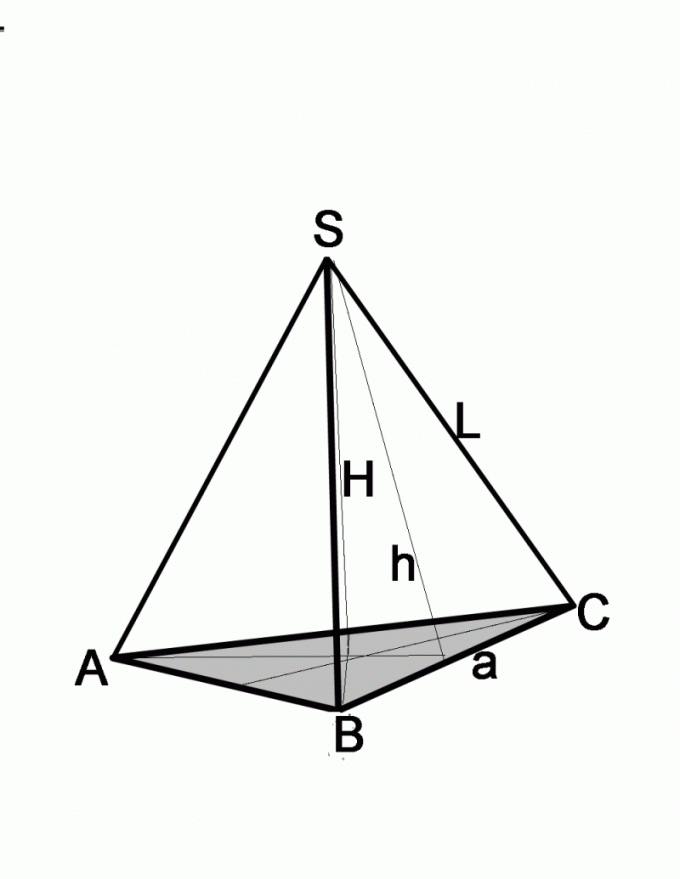
Если в задаче даны высота боковой грани и длина ребра, найдите сторону основания по теореме Пифагора. Боковая грань в данном случае будет гипотенузой, известная высота –з одним из катетов. Чтобы найти длину второго катета, нужно из квадрата гипотенузы вычесть квадрат второго катета, то есть (a/2)2=L2-h2, где а – сторона основания, L – длина боковой грани, h – высота боковой грани.

В этом случае нужно выполнить дополнительное построение, чтобы можно было оперировать тригонометрическими функциями. Вам даны боковое ребро L и высота пирамиды H, которая соединяет вершину пирамиды с центром основания. Из точки пересечения высоты с плоскостью основания проведите отрезок, соединив эту точку с одним из углов основания. У вас получился прямоугольный треугольник, гипотенузой которого является боковое ребро, одним из катетов – высота пирамиды. По этим данным легко найти второй катет треугольника, для этого достаточно из квадрата бокового ребра L вычесть квадрат высоты H. Дальнейшие действия зависят от того, какая именно фигура лежит в основании.

Вспомните свойства равностороннего треугольника. У него высоты одновременно являются биссектрисами и медианами. В точке пересечения они делятся пополам. То есть получается, что вы нашли половину высоты основания. Для удобства вычислений проведите все три высоты. Вы увидите, что отрезок, квадрат длины которого вы уже нашли, является гипотенузой прямоугольного треугольника. Извлеките квадратный корень. Вам известен и острый угол – 30°, так что найти половину стороны основания не составит особого труда, применив теорему косинусов.

Для пирамиды, в основании которой лежит правильный четырехугольник, алгоритм будет тем же самым. Если вы вычтите из квадрата бокового ребра квадрат высоты пирамиды, получите возведенную в квадрат половину диагонали основания. Извлеките корень, найдите размер диагонали, которая одновременно является гипотенузой равнобедренного прямоугольного треугольника. Размер любого из катетов найдите по теореме Пифагора, синусов или косинусов.

Высота и сторона основания правильной пирамиды

Свойства

Зная сторону основания правильной пирамиды, то есть пирамиды, в основании которой лежит правильный многоугольник, можно найти периметр основания, его площадь, радиус окружностей, которые можно вписать или описать около него, а также угол между сторонами многоугольника.

Периметр правильного многоугольника равен произведению длины его стороны на их удвоенное количество, а площадь представляет собой отношение количества сторон, умноженного на квадрат длины одной стороны, к четырем тангенсам 180 градусов, деленных на количество сторон. P=n(a+b) S=(na^2)/(4 tan⁡〖(180°)/n〗 )

Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1) r=a/(2 tan⁡〖(180°)/n〗 )

Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла.(рис.34.2) R=a/(2 sin⁡〖(180°)/n〗 )

Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3) γ=180°(n-2)/n

Параметры самой пирамиды, как объемного тела, такие как боковое ребро и апофема пирамиды вычисляются через теорему Пифагора в прямоугольном треугольнике с высотой во внутреннем пространстве пирамиды. Вторым катетом прямоугольного треугольника с апофемой является радиус вписанной окружности, а катетом треугольника с боковым ребром – радиус описанной окружности основания. (рис.34.4,34.5) l=√(h^2+r^2 )=√(h^2+(a/(2 tan⁡〖(180°)/n〗 ))^2 ) b=√(h^2+R^2 )=√(h^2+(a/(2 sin⁡〖(180°)/n〗 ))^2 )

Угол между апофемой и основанием рассчитывается как отношение синуса – высоты к радиусу вписанной окружности, а угол между боковым ребром и основанием аналогично – высоты к радиусу описанной окружности, из тех же прямоугольных треугольников. sin⁡α=h/r=(2h tan⁡〖(180°)/n〗)/a sin⁡β=h/R=(2h sin⁡〖(180°)/n〗)/a

Зная апофему и сторону основания пирамиды, можно найти площадь боковой поверхности, а затем площадь полной поверхности пирамиды. S_(б.п.)=lan/2 S_(п.п.)=an(l/2+a/(4 tan⁡〖(180°)/n〗 ))

Объем пирамиды равен трети произведения площади основания на высоту, таким образом, зная высоту и сторону основания пирамиды, вычислить ее объем можно, подставив соответствующее выражение вместо площади основания. V=1/3 S_(осн.) h=(na^2 h)/(12 tan⁡〖(180°)/n〗 )

В любую правильную пирамиду (в основании которой лежит правильный многоугольник) можно вписать сферу, а также описать сферу около нее. Радиусы вписанной и описанной сфер зависят не только от высоты и стороны основания, но и от объема пирамиды, площади полной поверхности и бокового ребра пирамиды, поэтому для их вычисления необходимо произвести алгебраические преобразования формул. (рис.34.6,34.7) r_1=3V/S_(п.п.) =ah/(tan⁡〖(180°)/n〗 (2l+a/tan⁡〖(180°)/n〗 ) ) R_1=b^2/2h=(h^2+(a/(2 sin⁡〖(180°)/n〗 ))^2)/2h

Источник

Что такое пирамида: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение пирамиды

Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.

Примечание: пирамида – это частный случай конуса.

Элементы пирамиды

Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.

Примечание: свойства пирамиды представлены в отдельной публикации.

Виды сечения пирамиды

1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):

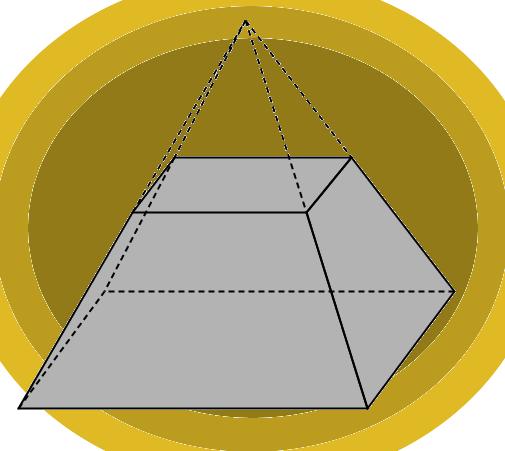
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.

Примечание: Существуют и другие виды сечения, но они не так распространены.

Источник

Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида

Геометрические представления о фигуре

Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.

Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.

Правильная пирамида

Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.

Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.

Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.

Сторона основания, высота, боковое ребро и апотема

Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.

Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.

Для высоты h получаем выражение:

Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.

Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:

Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.

Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.

Объем фигуры

Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:

Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:

Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:

То есть он определяется длиной стороны a однозначно.

Площадь поверхности

Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.

Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:

Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.

Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:

Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.

Полная площадь поверхности фигуры равна:

S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a

Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:

Свойства правильной усеченной пирамиды треугольной

Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.

В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.

Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.

Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:

S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)

Объем фигуры рассчитывается следующим образом:

V = √3/12*h*(a12 + a22 + a1*a2)

Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.

Источник

Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида

Что такое пирамида в общем случае?

В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Правильная четырехугольная пирамида

Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Площадь и объем фигуры

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

Свойства правильной усеченной четырехугольной пирамиды

Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Источник

Пирамида

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Виды пирамид

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Источник

Пошаговое построение сечения четырехугольной пирамиды

Сегодня научимся строить сечения четырехугольной правильной пирамиды. Использовать для построения будем метод следов. Пользоваться этим методом  неудобно и даже иногда невозможно, когда сечение имеет малый наклон или не имеет наклона к плоскости основания. Если такой случай вам попадется, лучше использовать метод внутреннего проецирования.

Задача 1.

Построить сечение четырехугольной правильной пирамиды  плоскостью, проходящей через точки  .

Шаг 1. Через точки и , принадлежащие плоскости грани , проведем прямую . Определим точку плоскости основания пирамиды, которая бы принадлежала и секущей плоскости. Для этого проведем продолжение ребра и найдем точку его пересечения с прямой – точка .

Шаг 2. Аналогично найдем вторую точку секущей плоскости в плоскости основания: проводим  прямую , находим ее пересечение с продолжением ребра – точка .

Шаг 3. Через две точки можно провести прямую, и, так как точки и принадлежат и секущей плоскости, и плоскости основания, то и прямая, проведенная через них, будет принадлежать обеим плоскостям. А раз эта прямая лежит в плоскости основания, то определим точки пересечения этой прямой с другими прямыми плоскости основания, например, с продолжением ребра – точка , и продолжением ребра – точка . Значит, точки   и – тоже точки плоскости сечения, а за счет того, что прямая лежит в плоскости грани , точка также принадлежит плоскости этой грани. Аналогично, так как прямая принадлежит плоскости грани , то и точка – точка этой же плоскости. Теперь можно соединить точки и – как точки одной плоскости, и соединить точки и .

Шаг 4. Пересечение прямых и даст нам последнюю точку искомого сечения – точку .

Проводим отрезки , , завершая построение:

Окончательный вид сечения:

Задача 2.

Построить сечение четырехугольной правильной пирамиды  плоскостью, проходящей через точки  .

Шаг 1. Проводим прямую , она принадлежит грани , так как точки и принадлежат ей.

Шаг 2. Прямая пересечет прямую , и точка их пересечения   благодаря принадлежности прямой будет лежать в  плоскости основания.

Шаг 3. Точки и принадлежат плоскости основания, проведем через них прямую ,  найдем точку пересечения этой прямой ребра – точку . Продлим прямую до пересечения с прямой , получим точку . Точка принадлежит плоскости , тк как этой плоскости принадлежит прямая .

Шаг 4. Соединим точки и . Найдем место пересечения данной прямой ребра – точку .

Шаг 5. Соединяем полученные точки отрезками.

Окончательный вид с другого ракурса:

Задача 3.

Построить сечение четырехугольной правильной пирамиды  плоскостью, проходящей через точки  .

Шаг 1. Соединим и , как точки одной плоскости.

Шаг 2. Прямая принадлежит плоскости грани , следовательно, пересечет прямую этой же грани . Найдем точку их пересечения , продлив ребро  .

Шаг 3.  Точки и – “одного поля ягоды” – обе принадлежат плоскости грани . Поэтому соединим их, отметив точку пересечения с ребром – .

Шаг 4. Точки и принадлежат плоскости основания, соединяем их.  Прямая лежит в плоскости основания и пересечет прямую  в точке .

Шаг 5. Точки и соединяем, так как обе они принадлежат плоскости , и получаем последнюю точку сечения – на ребре .

Шаг 6. Соединяем точки отрезками.

Окончательный вид сечения:

Задача 4.

Построить сечение четырехугольной правильной пирамиды  плоскостью, проходящей через точки  .

Шаг 1-2. Точки и принадлежат грани , соединим их отрезком (прямой). Точки и принадлежат грани основания, также соединим их.

Шаг 3. Прямая пересечет продолжение ребра в точке . Точка , таким образом, принадлежит плоскости грани .

Шаг 4.  Соединяем точки и , проводя прямую . Она пересечет ребро в точке .

Шаг 5. Соединяем полученные точки на ребрах отрезками:

Окончательный вид с удобного ракурса:

4 комментария

На этой странице вы узнаете

• Как дракон с помощью сечений разрушал город?
• Чем вода похожа на сечение?
• Что общего у следа на снегу и следа в сечении?

Заглянем в кинотеатр имени Математики. Какой фильм сейчас будут показывать? Располагайтесь поудобнее, приятного просмотра… 

Сечения

Как дракон с помощью сечений разрушал город?

…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм. 

Но внезапно с другой, темной стороны планеты, появился дракон, коренной обитатель планеты. Ему не понравилось вторжение людей, и решил он стереть в пыль все строения. 

Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии. 

Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость. 

Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника. 

Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры. 

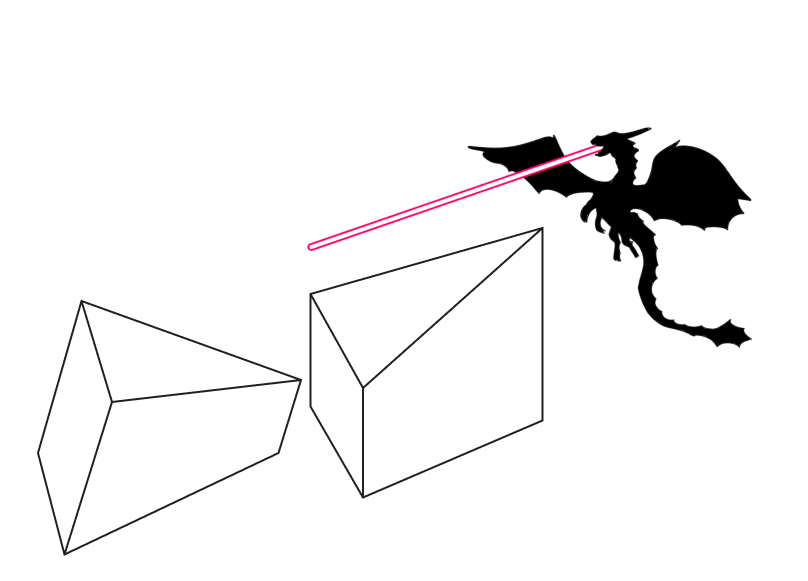
Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания. 

Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.

Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. 

Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно. 

Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях. Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.

Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах. 

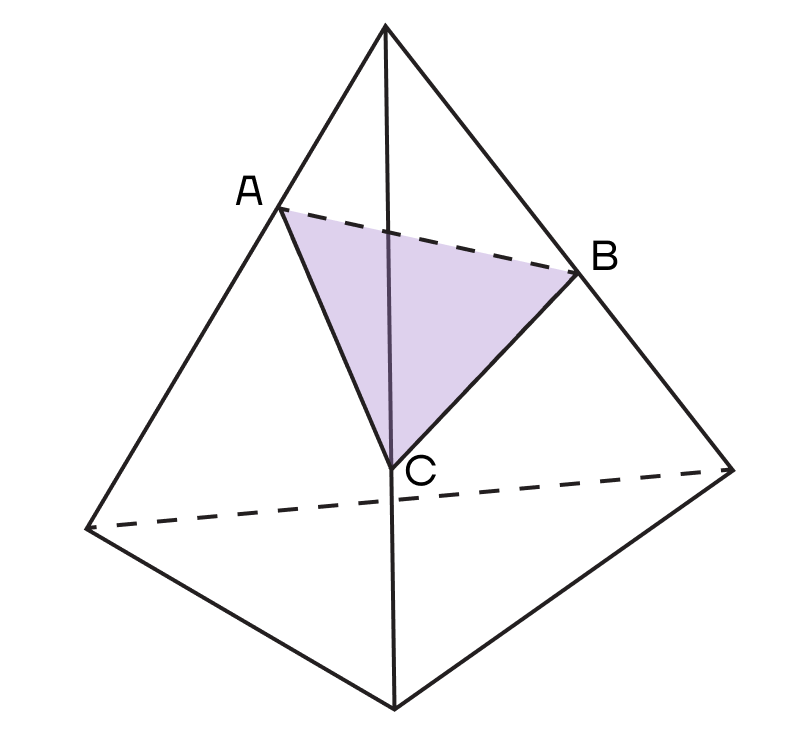
При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости. 

Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии. В этой статье мы не будем заострять на них внимание,  прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве». 

Зачем может потребоваться сечение? 
Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни. 

Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.

А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”. 

Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.

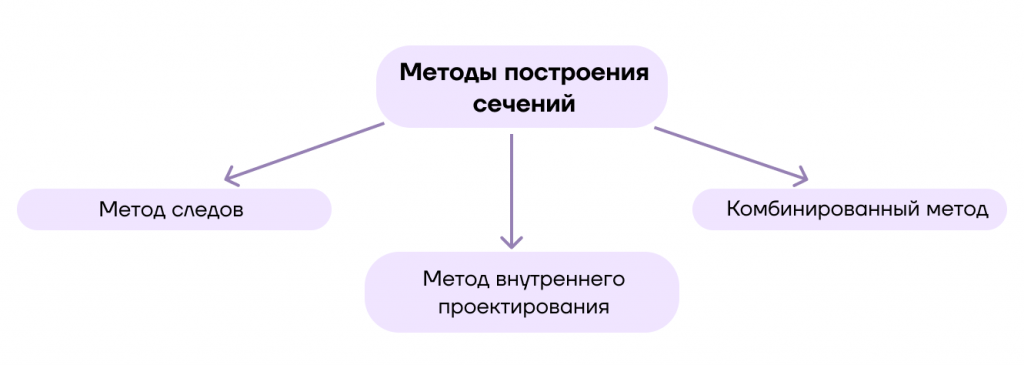
Методы построения сечений

Однако сечения нужно правильно построить. Для их построения существует несколько методов:

• Метод следов;
• Метод внутреннего проектирования;
• Комбинированный метод.

Разберем их по порядку.

Зимой очень интересно гулять по лесу и разглядывать следы животных: вот пробежал заяц, а это, кажется, была маленькая лисица. Здесь просто снег упал с веток дерева. 

Все эти тела оставляют след на снегу. 

Если мы возьмем карандаш и проведем прямую на листе, он оставит след. Также и плоскость сечения как бы проводит карандашом по граням фигур, оставляя после себя следы. 

След плоскости а в плоскости основания многогранника — прямая, по которой секущая плоскость пересекает плоскость основания многогранника. 

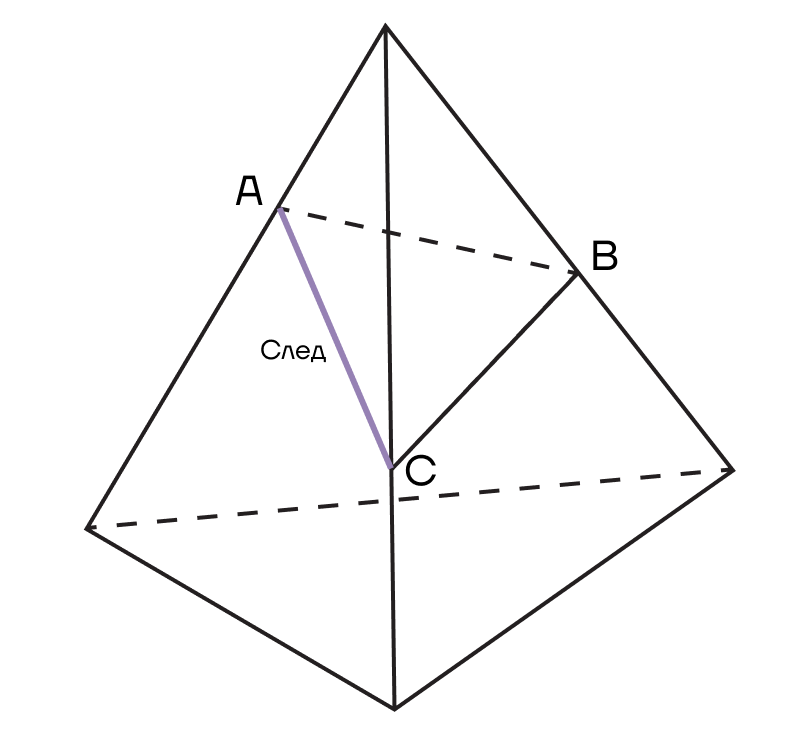
Вспомним, что плоскость бесконечна, значит, и след можно продолжать в разные стороны бесконечно. 

Однако для построения сечений необходимости бесконечно его продолжать нет: достаточно до пересечения с ребром многогранника или продолжением ребра. 

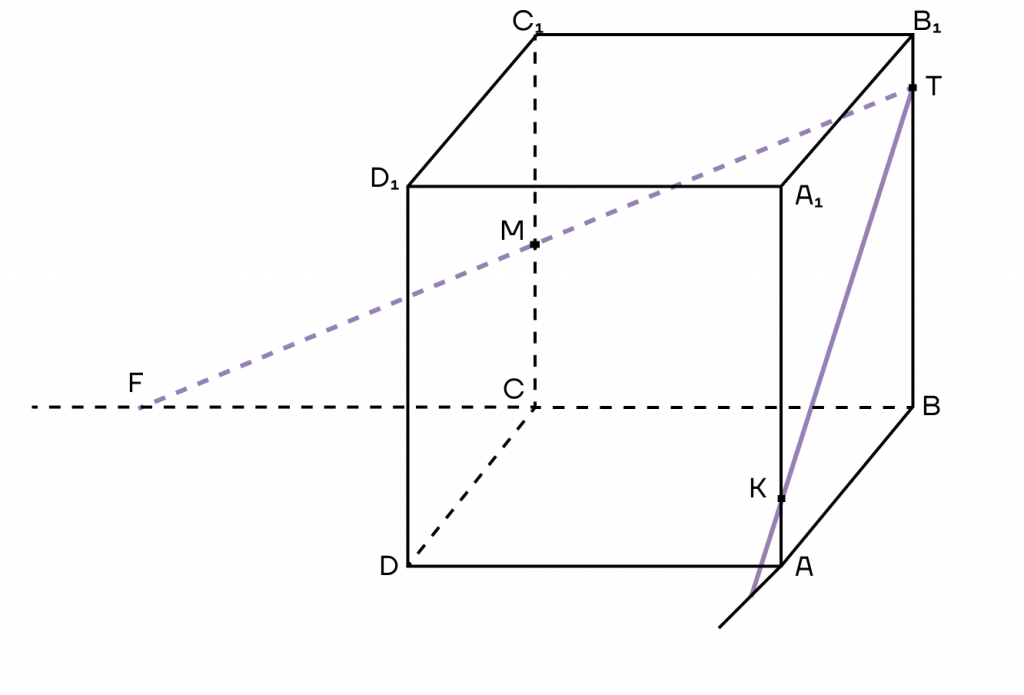
Построим сечение куба, которое проходит через точки К, М и Т, чтобы  чуть подробнее разобраться в методе следов. 

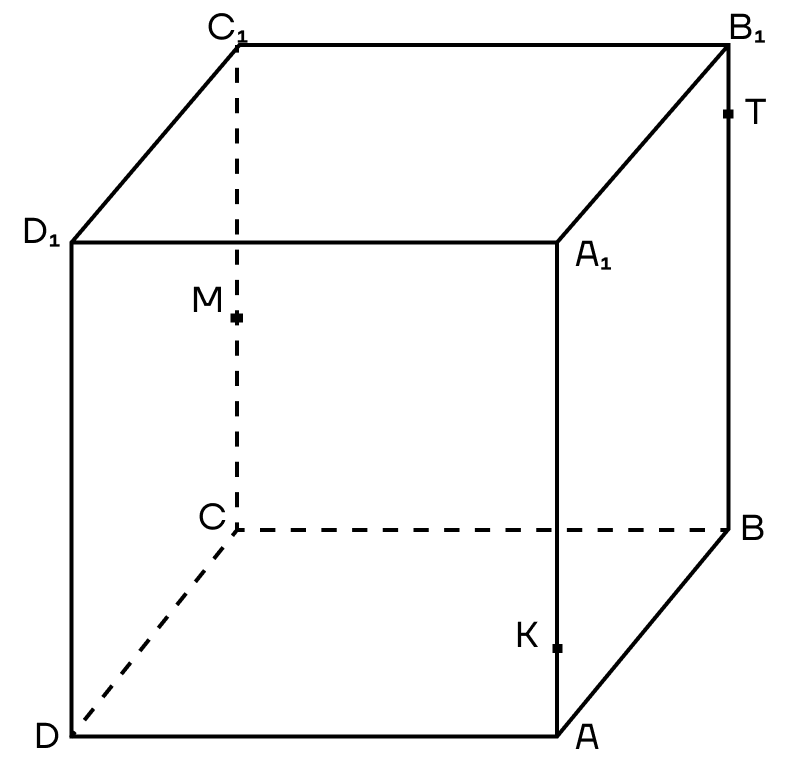
При построении сечений существует очень важный лайфхак: если точки лежат в одной плоскости (то есть в одной грани), то их можно соединить. 

1. Заметим, что в нашем кубе это точки К и Т в плоскости (АВВ₁) и точки М и Т в плоскости (ВСС₁). Поэтому мы можем их соединить. 

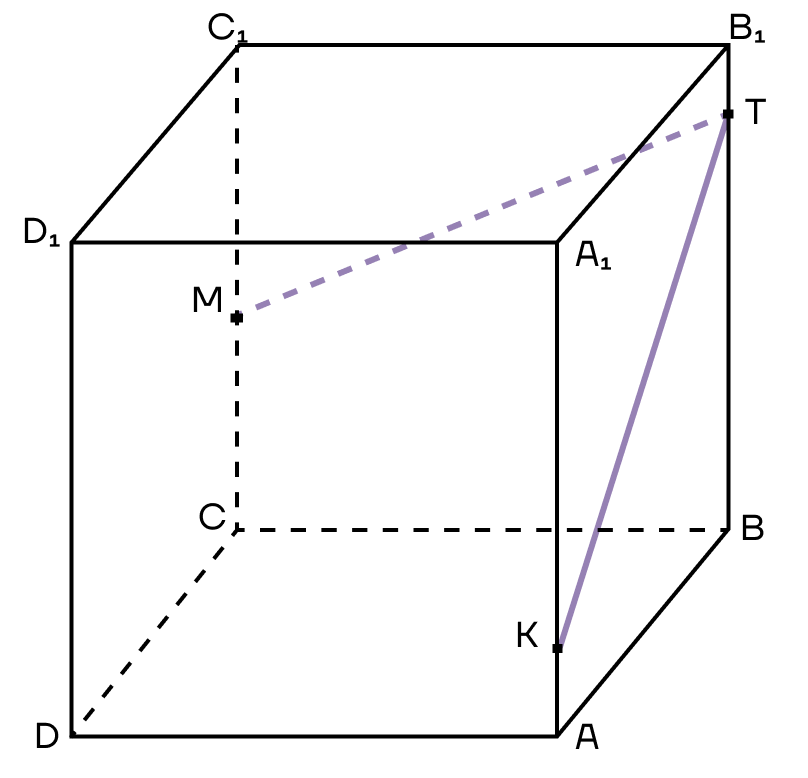
2. КТ и МТ в нашем случае — это следы плоскости сечения. Продолжим их за точку К и за точку М. Аналогично продолжим стороны АВ и ВС до тех пор, пока их продолжения не пересекутся со следами. 

Пусть продолжения прямых АВ и ТК пересекутся в точке Н, а продолжения прямых ТМ и ВС пересекутся в точке F. 

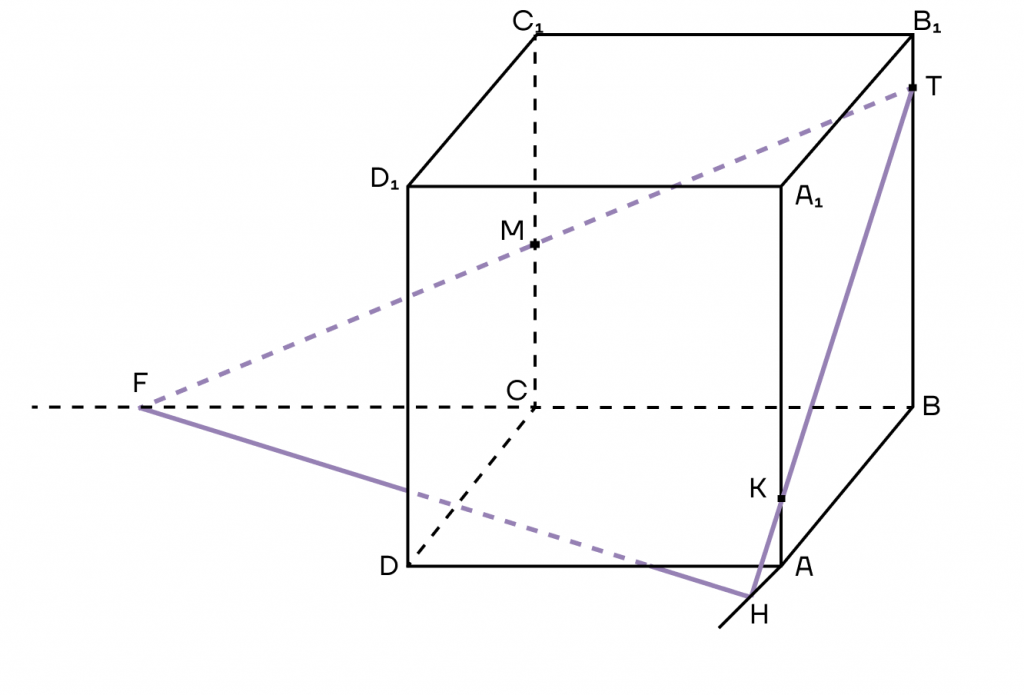
3. Обратим внимание, что точки Н и F лежат на продолжении ребер основания, а значит, лежат в плоскости основания куба. Пользуясь лайфхаком, их можно соединить. Таким образом, получим треугольник, который как бы разрезает наш куб. 

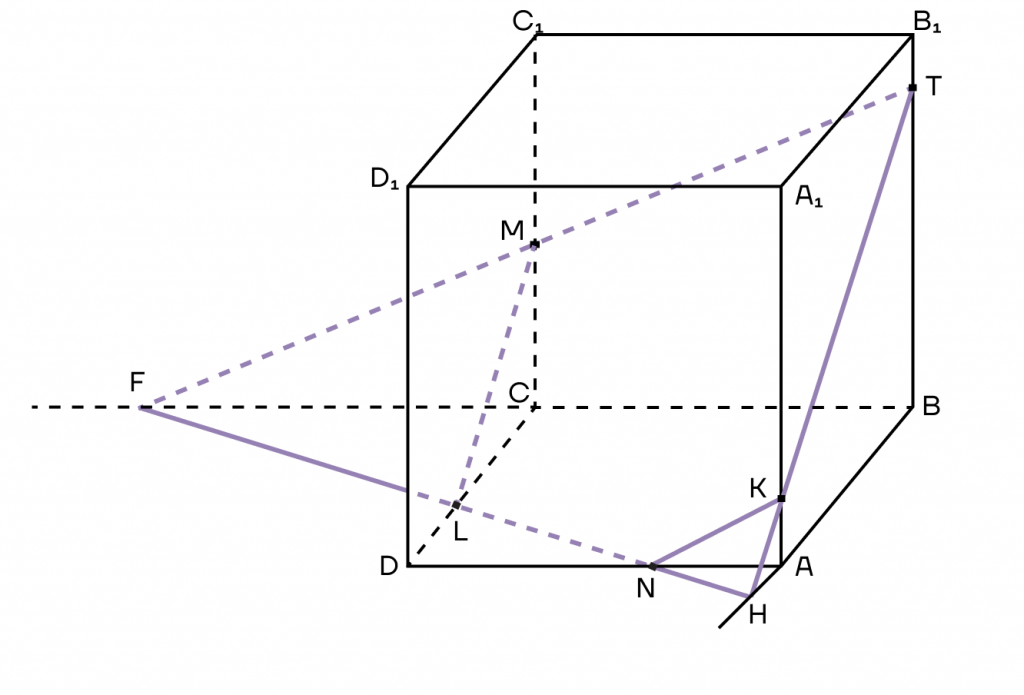
4. Однако наше сечение не закончено. Вспомним, что все вершины многоугольника должны лежать на ребрах куба, то есть точки Н и F не подходят. Но на самом деле осталось совсем немного закончить построение.

5. Заметим, что прямая HF пересекает ребра AD, DC, назовем точки этих пересечений как N и L. 

А также соединим все точки, которые окажутся в одной плоскости. 

6. И вот мы получили сечение. Многоугольник TKNLM — сечение куба. 

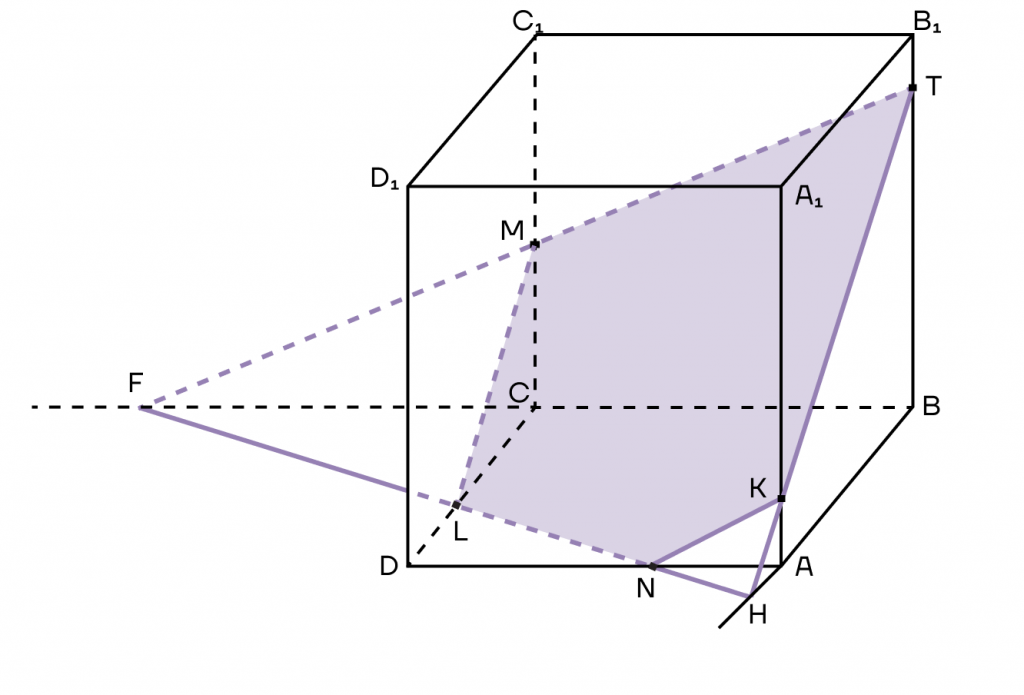
Итак, основной способ построить сечение методом следов — продолжить след сечения до его пересечения с ребрами многогранника или продолжениями его ребер. 

А также пользоваться лайфхаком: точки в одной плоскости можно соединять. 

Рассмотрим метод внутреннего проектирования. 

Иногда метод следов может не помочь: след будет идти параллельно ребру или пересекаться с его продолжением далеко за пределами листа. 

В таких случаях часто используется следующее свойство: параллельные плоскости пересекаются другой плоскостью по параллельным прямым. Подробнее про это свойство можно прочесть в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве». 

Польза этого свойства в том, что если сечение пройдет через параллельные плоскости, то оно пересечет их по параллельным линиям. А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.

Но будем разбираться на практике. Построим сечение треугольной призмы, проходящее через точки К, М, Т. 

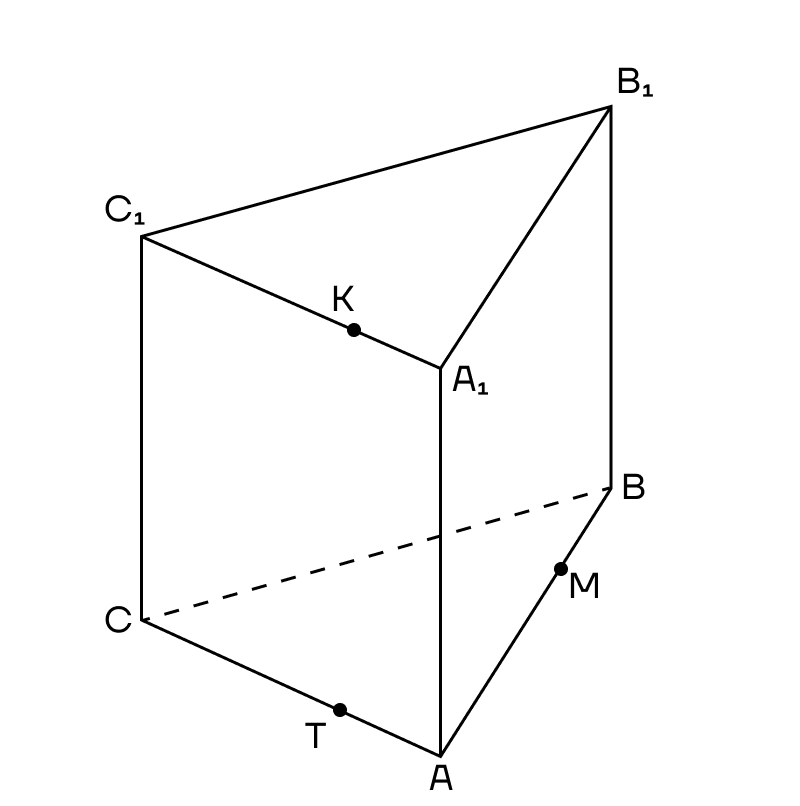
1. Первым делом соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС₁) и точки Т и М в плоскости (АВС). 

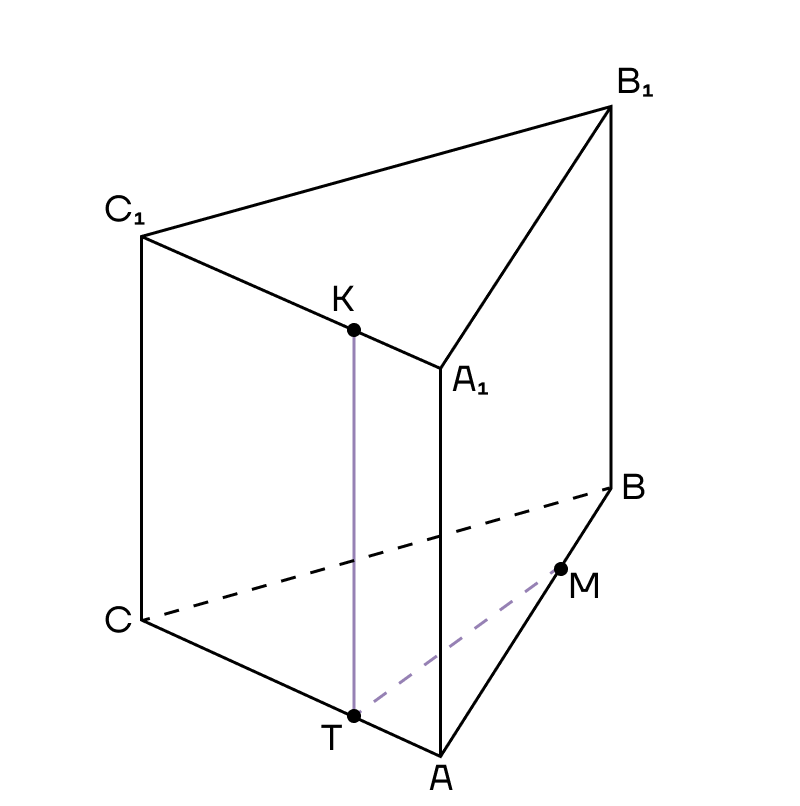
2. КТ проходит почти параллельно ребру АА₁, следовательно, использовать метод следов не рационально. 

3. Теперь посмотрим на плоскости (АВС) и (А₁В₁С₁) — они параллельные. А значит прямую сечения можно параллельно перенести в одну из них. 

В плоскости (АВС) лежит прямая ТМ, а в плоскости (А₁В₁С₁) лежит точка К, которая является вершиной сечения. Тогда из точки К в плоскости верхнего основания нам нужно провести прямую, параллельную ТМ до пересечения с ребром призмы. Назовем эту точку Е.

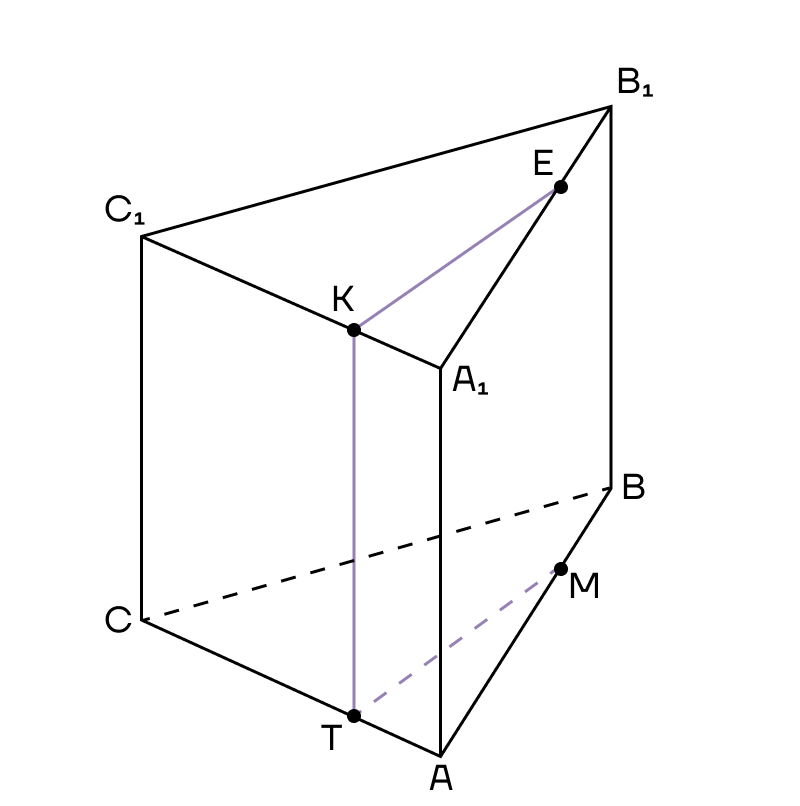
4. А теперь мы можем соединить Е и М, так как они лежат в одной плоскости. Четырехугольник КЕМТ — сечение призмы. 

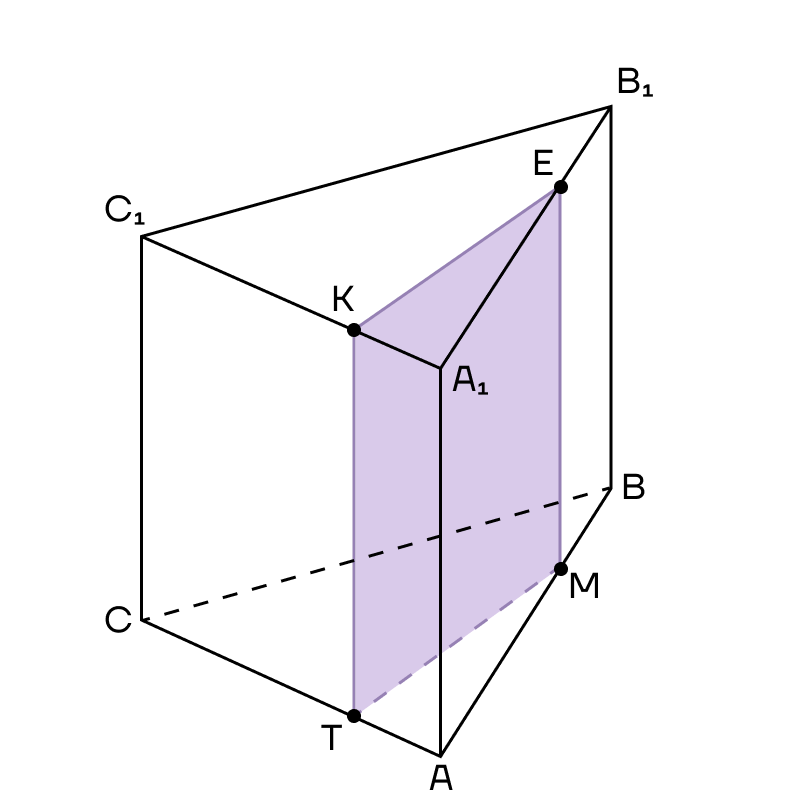
Осталось разобраться, в чем заключается комбинированный метод? Он включает в себя и метод следов, и метод внутреннего проектирования, то есть приемы из каждого метода могут применяться вместе в одной и той же задаче.

Все зависит от удобства решения и его быстроты: там, где невозможно применить метод внутреннего проектирования, можно применить метод следов. А там, где применять метод следов неудобно (или невозможно), можно применить метод внутреннего проектирования. 

Примеры построения сечений

Рассмотрим несколько примеров построения сечений в различных фигурах. 

Пример 1. В правильном тетраэдре провели апофему АТ, на середине которой отметили точку К. АЕ:ЕС = 1:5. Р — точка на ребре CD. Постройте сечение тетраэдра, проходящее через точки К, Е и Р. 

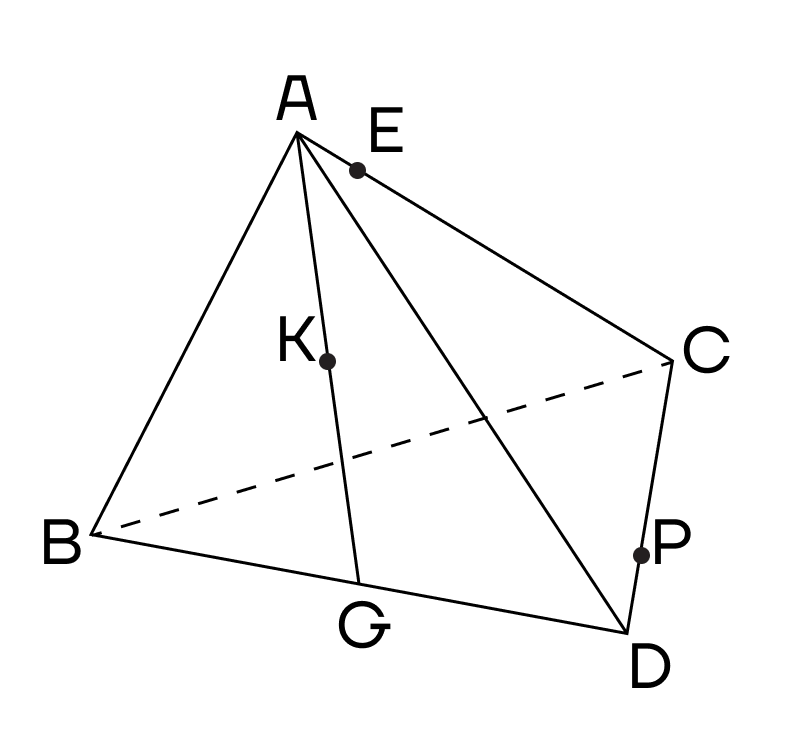
Решение. Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию. 

1. Начнем решение с того, что соединим точки, лежащие в одной плоскости. Е и Р лежат в плоскости (ACD), значит их можно соединить. 

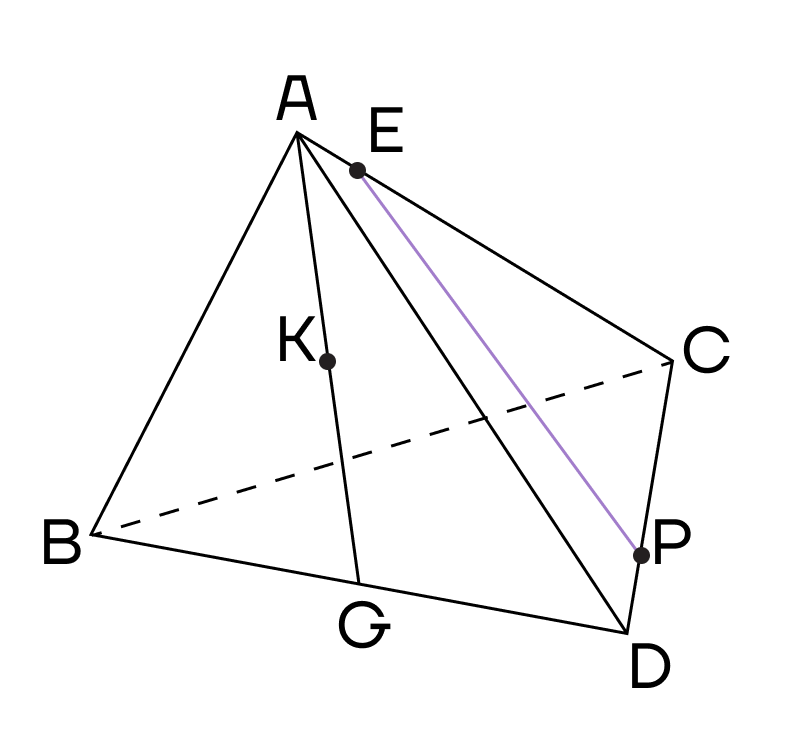
2. Рассмотрим плоскость (АСG). Проведем прямую CG. Точки К и Е лежат в одной плоскости, то есть их также можно соединить. 

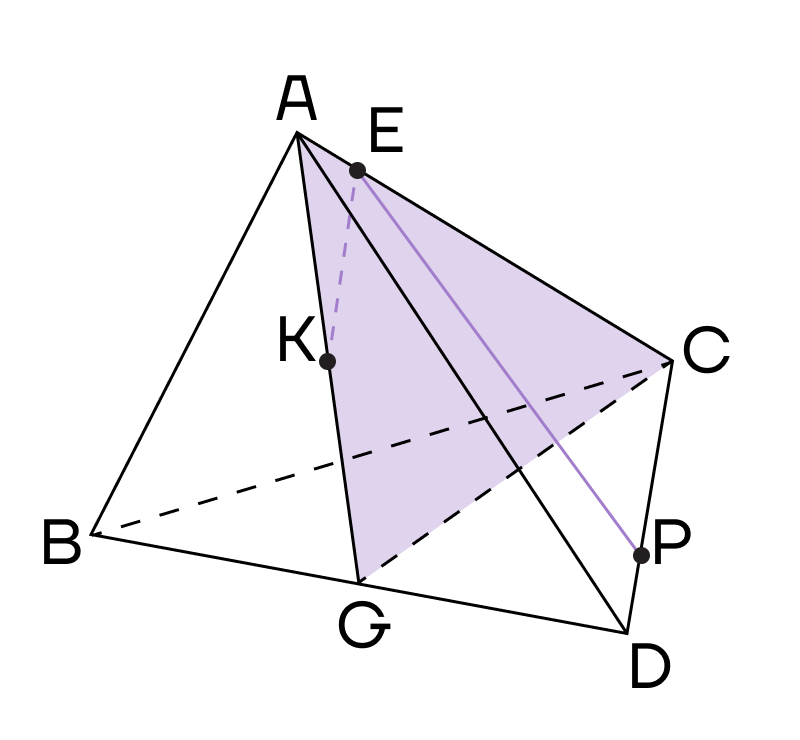
3. Воспользуемся методом следов и продлим прямые ЕК и CG до их пересечения в точке Т. 

4. Теперь точки Т и Р будут лежать в одной плоскости основания, следовательно, их можно соединить. Пусть прямая ТР пересекает ребро BD в точке М. 

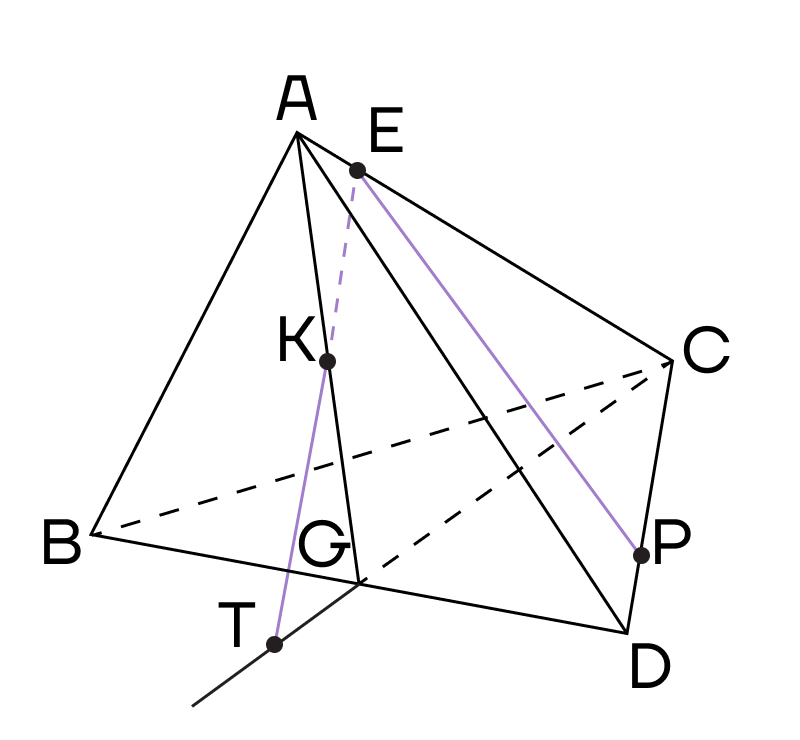
Тогда точки М и К лежат в одной плоскости (ABD) — их тоже можно соединить. 

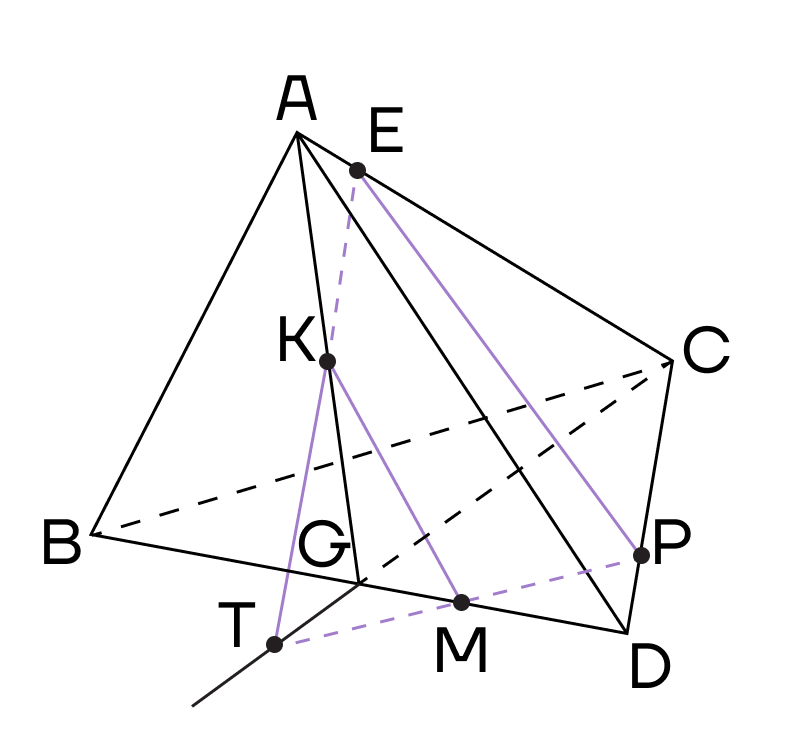
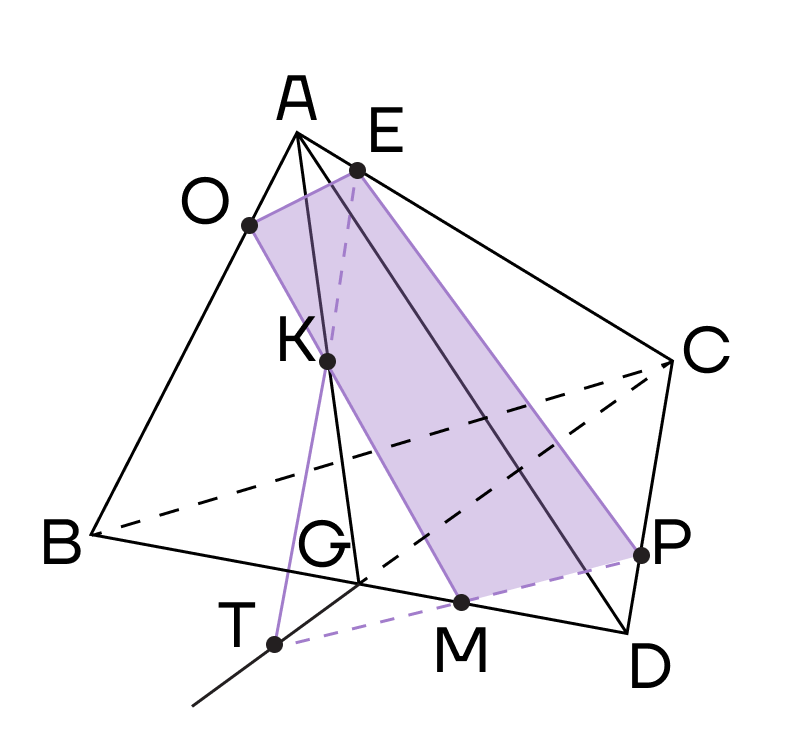
5. Продлим прямую МК до пересечения с ребром АВ в точке О. Точки О и Е лежат в одной плоскости (АВС), соединим их. Сечением тетраэдра будет четырехугольник ОЕРМ. 

Пример 2. Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т. 

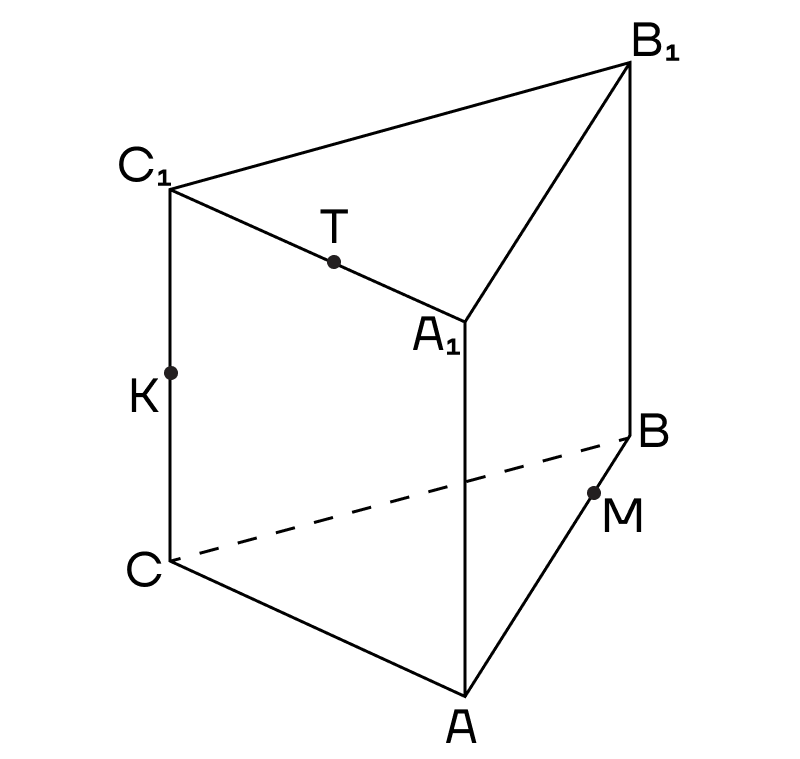
Решение. 1. Соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС₁). 

Воспользуемся методом следов и продолжим прямую ТК до пересечения с продолжением стороны АС в точке Р.

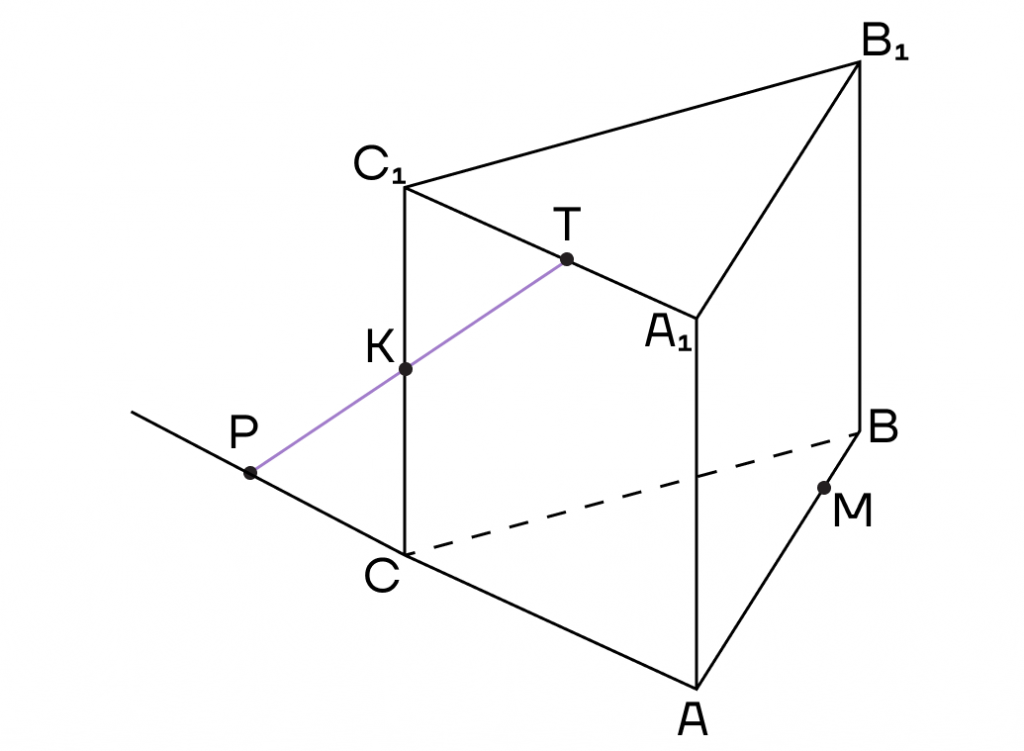
2. Точки Р и М лежат в одной плоскости (АВС), то есть их можно соединить. Пусть прямая РМ пересечет ребро ВС в точке Е. 

Воспользуемся методом внутреннего проектирования и проведем из точки Т прямую, параллельную ЕМ. Пусть она пересечет ребро А₁В₁ в точке О. 

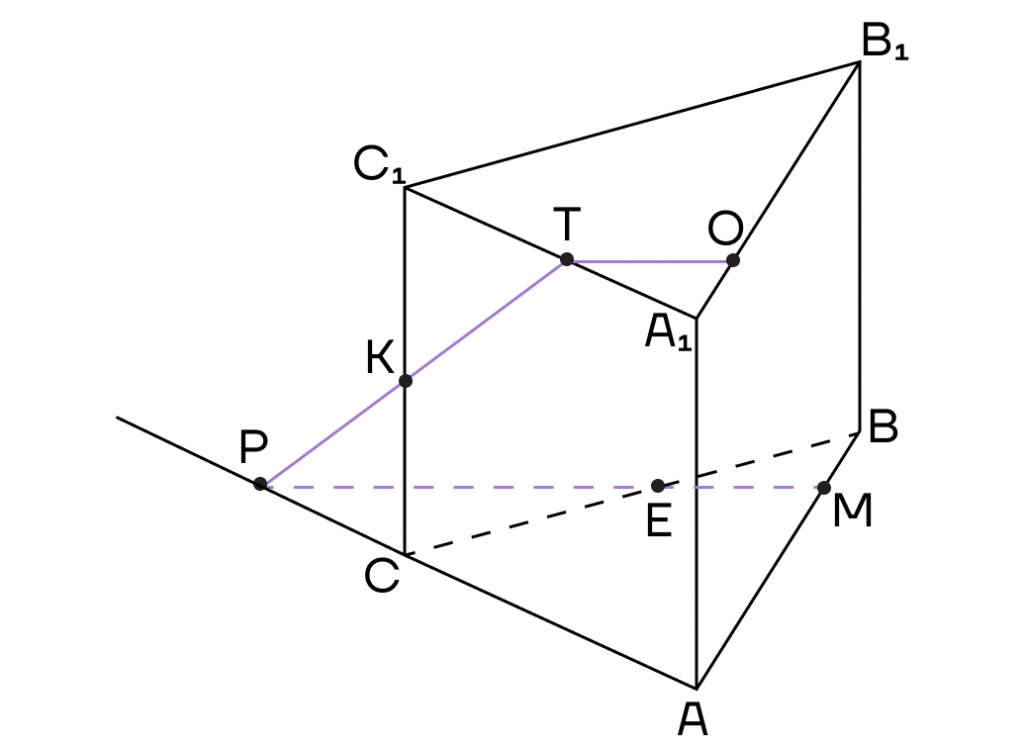
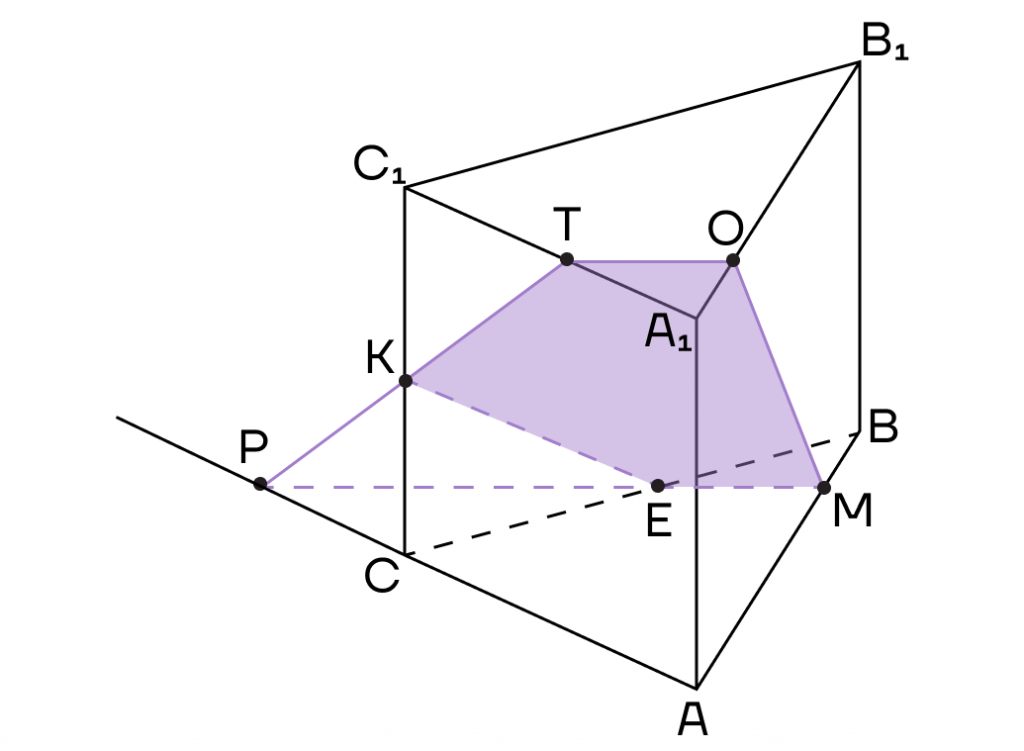
3. Осталось соединить точки, лежащие в одной плоскости. Это точки К и Е в плоскости (ВСС₁) и точки О и М в плоскости (АВВ₁). 

Тогда КТОМЕ — сечение призмы. 

Пример 3. Дан куб ABCDA₁B₁C₁D₁. М — середина ребра АА₁. Постройте сечение куба, которое будет параллельно диагонали куба А₁С и будет проходить через точки М и В.

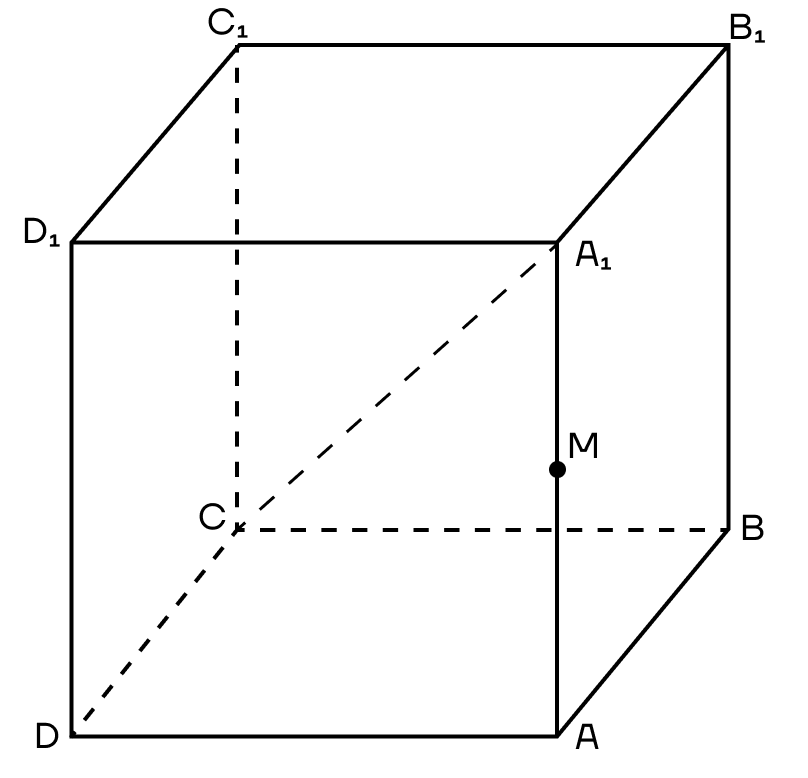
Решение. 1. Достроим прямую АС и рассмотрим плоскость (АА₁С). Проведем в ней прямую, параллельную А₁С из точки М. Пусть она пересечет АС в точке К. 

2. Тогда МК — средняя линия треугольник АА₁С, значит К — середина АС. 

Подробнее про среднюю линию треугольника можно прочесть в статье «Треугольники». 

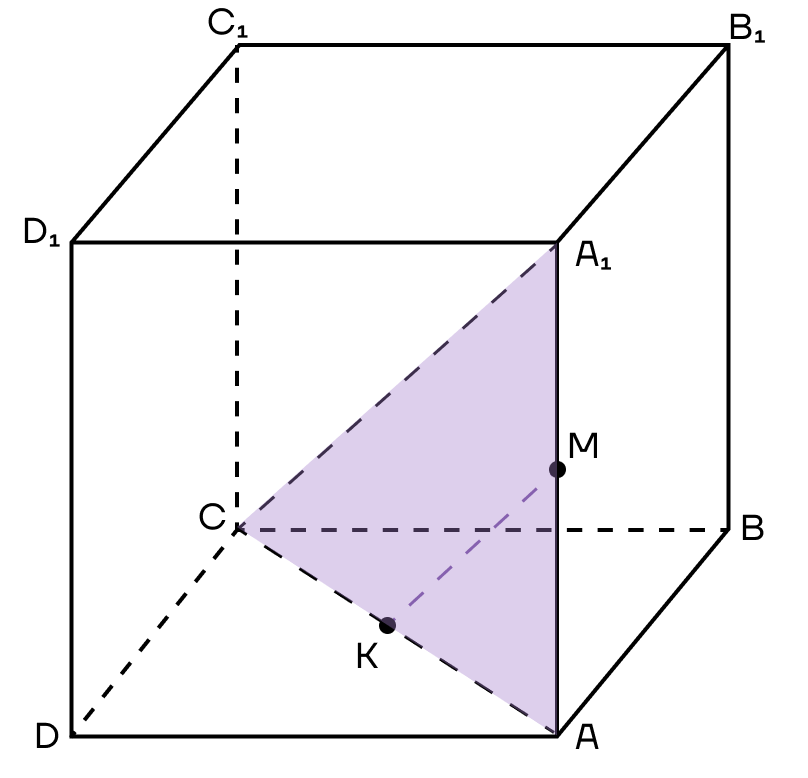
3. Точка К будет принадлежать сечению. Точки В и К лежат в плоскости (АВС) —  их можно соединить. 

4. В основании куба находится квадрат, его диагонали равны и точкой пересечения делятся пополам. 

Подробнее про квадрат и его свойства можно прочитать в статье «Параллелограмм». 

Поскольку К — середина диагонали АС, эта же точка будет серединой диагонали BD. 

Следовательно, прямую ВК можно продлить до точки D. 

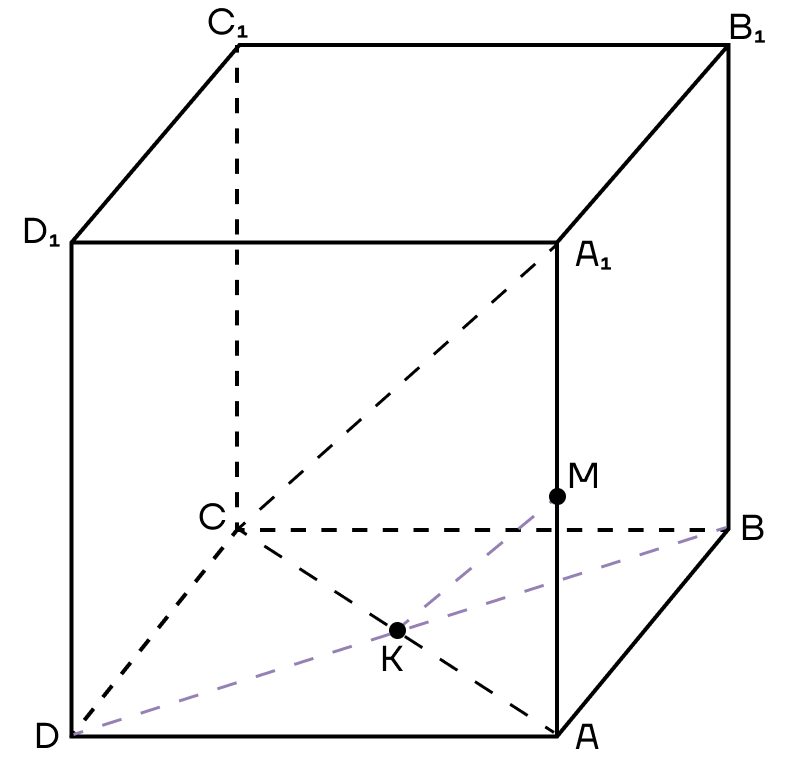
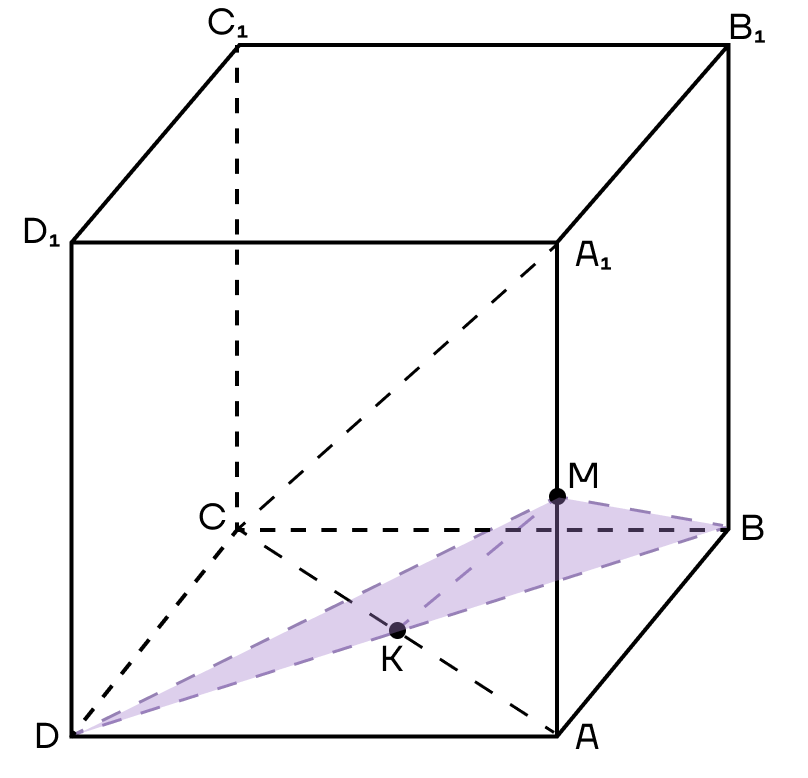
5. Осталось только соединить точки, которые лежат в одной плоскости. Это точки М и D в плоскости (ADD₁) и точки М и В в плоскости (ABB₁). 

Тогда сечением будет треугольник DMB. 

Мы рассмотрели сечения и основные способы их построения. В них нет ничего сложного и стоит помнить, что любое сечение можно представить в реальной жизни. Например, попробовать разрезать пластилиновые фигуры. 

Фактчек

• Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. При этом в многогранниках сечения представлены в виде многоугольников, вершины которых лежат на ребрах фигуры.
• Существует несколько методов построения сечения в многогранниках: метод следов, метод внутреннего проектирования и комбинированный метод. 
• Метод следов заключается в том, что по следу сечения можно построить его полностью. След сечения — прямая, по которой секущая плоскость пересекает грань многогранника. В методе следов часто нужно продлевать линии и ребра до их пересечения.
• Метод внутреннего проектирования позволяет параллельно переносить сторону сечения в параллельных плоскостях. Это может быть удобно в случаях, когда метод следов невозможно или трудно применить. 
• Комбинированный метод — метод, который сочетает в себе и метод следов, и метод внутреннего проектирования. 

Проверь себя

Задание 1. 
Какая форма сечения будет, если треугольную пирамиду разрезать параллельно основанию?

1. Треугольник;
2. Четырехугольник;
3. Шестиугольник;
4. Произвольный многоугольник с любым количеством углов. 

Задание 2.
Где могут лежать вершины многоугольника, который образовывает сечение?

1. Только в вершинах многогранника;
2. На ребрах многогранника;
3. Только на гранях многогранника;
4. В любой точке на многограннике. 

Задание 3.
Что такое след сечения?

1. Продолжения сторон сечения;
2. Вершины многоугольника, который образовывает сечение;
3. Прямая, по которой секущая плоскость пересекает плоскость основания многогранника;
4. Все вышеперечисленные варианты. 

Задание 4.
Что можно сделать с точками, которые лежат на одной грани?

1. Соединить;
2. Ни в коем случае нельзя их соединять;
3. Построить сечение, опираясь на две разные стороны, не соединяя стороны;
4. Ни один из перечисленных вариантов. 

Задание 5.
Как можно воспользоваться методом внутреннего проектирования?

1. Произвольно переносить линии сечения в любых гранях;
2. Произвольно переносить линии сечения в параллельных гранях;
3. Перпендикулярно переносить линии сечения в перпендикулярных гранях;
4. Параллельно переносить линии сечения в параллельных гранях. 

Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 4

Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса – треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.

Геометрические представления о фигуре

Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.

Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Вам будет интересно:Лихой – это: значение и синонимы

Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней – это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.

Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.

Правильная пирамида

Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.

Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.

Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.

Сторона основания, высота, боковое ребро и апотема

Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.

Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.

Для высоты h получаем выражение:

h = √(b2 – a2/3)

Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.

Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:

ab = √(b2 – a2/4)

Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.

Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.

Объем фигуры

Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:

V = 1/3*So*h

Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:

V3 = √3/12*a2*h

Где высота правильной треугольной пирамиды равна h, а ее сторона основания – a.

Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:

V = √2/12*a3

То есть он определяется длиной стороны a однозначно.

Площадь поверхности

Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.

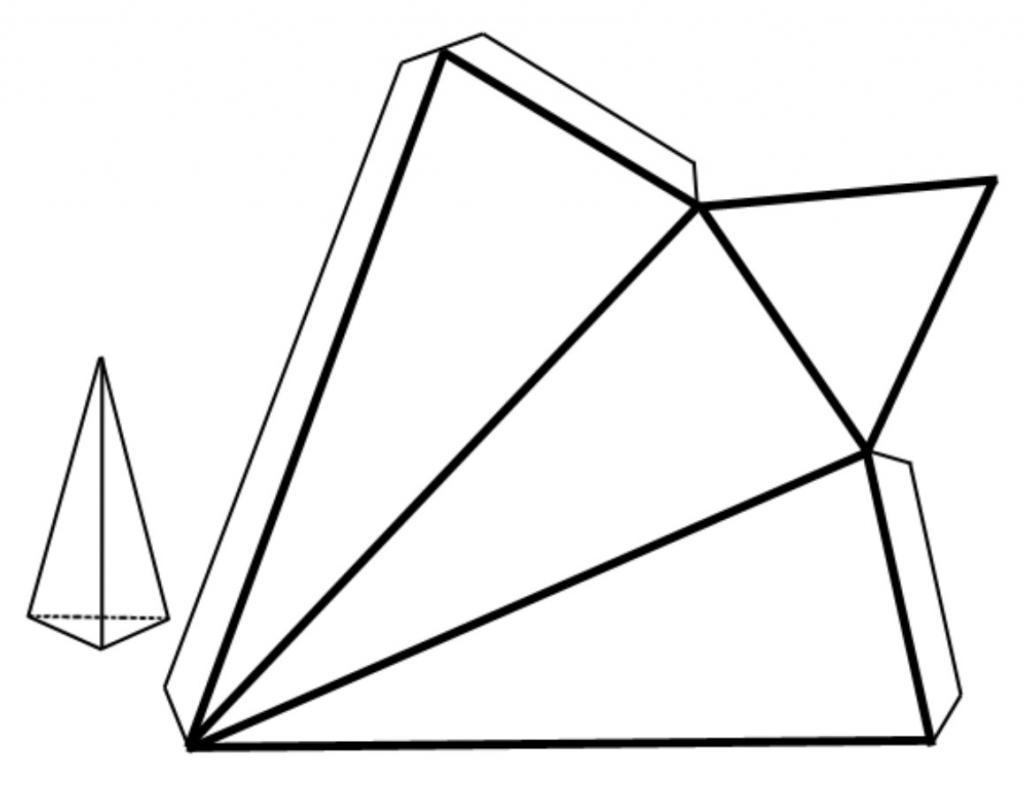
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:

So = √3/4*a2

Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.

Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:

Sb = 3/2*√(a2/12+h2)*a

Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.

Полная площадь поверхности фигуры равна:

S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a

Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:

S = √3*a2

Свойства правильной усеченной пирамиды треугольной

Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.

В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.

Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.

Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:

S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)

Здесь первое слагаемое – это площадь боковой поверхности, второе слагаемое – площадь треугольных оснований.

Объем фигуры рассчитывается следующим образом:

V = √3/12*h*(a12 + a22 + a1*a2)

Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.