Как найти сторону шестиугольника если известна площадь

Как найти сторону правильного шестиугольника

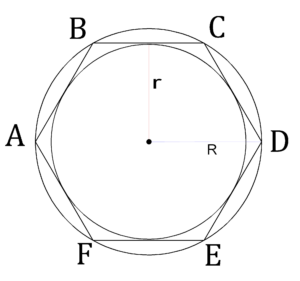
Шестиугольную – «гексагональную» – форму имеют, например, сечения гаек и карандашей, пчелиных сот и снежинок. Правильные геометрические фигуры такой формы имеют некую особенность, отличающую их от прочих плоских многоугольников. Заключается она в том, что радиус описанной около гексагона окружности равен длине его стороны – во многих случаях это значительно упрощает вычисление параметров многоугольника.

Инструкция

Если в условиях задачи дан радиус (R) описанной около правильного шестиугольника окружности, вычислять ничего не придется – эта величина тождественна длине стороны (t) гексагона: t = R. При известном диметре (D) просто поделите его пополам: t = D/2.

Периметр (Р) правильного шестиугольника позволяет вычислить длину стороны (t) простой операцией деления. В качестве делителя используйте число сторон, т.е. шестерку: t = Р/6.

Радиус (r) вписанной в такой многоугольник окружности связан с длиной его стороны (t) немного более сложным коэффициентом – удвойте радиус, а полученный результат разделите на квадратный корень из тройки: t = 2*r/√3. Эта же формула с использованием диаметра (d) вписанной окружности станет на одно математическое действие короче: t = d/√3. Например, при радиусе в 50 см длина стороны шестиугольника должна быть приблизительно равна 2*50/√3 ≈ 57,735 см.

Известная площадь (S) многоугольника с шестью вершинами тоже позволяет вычислить длину его стороны (t), но численный коэффициент, связывающий их, точно выражается через дробь из трех натуральных чисел. Две трети площади делите на квадратный корень из тройки, а из полученного значения извлекайте квадратный корень: t = √(2*S/(3*√3)). Например, если площадь фигуры составляет 400 см², длина ее стороны должна составлять примерно √(2*400/(3*√3)) ≈ √(800/5,196) ≈ √153,965 ≈ 12,408 см.

Длина окружности (L), описанной около правильного шестиугольника, связана с радиусом, а значит и с длиной стороны (t) через число Пи. Если он дана в условиях задачи, поделите ее величину на два числа Пи: t = L/(2*π). Скажем, если эта величина равна 400 см, длина стороны должна составлять приблизительно 400/(2*3,142) = 400/6,284 ≈ 63,654 см.

Этот же параметр (l) для вписанной окружности позволяет рассчитать длину стороны шестиугольника (t) вычислением соотношения между ней и произведением числа Пи на квадратный корень из тройки: t = l/(π*√3). Например, если длина вписанной окружности составляет 300 см, сторона шестиугольника должна иметь величину, примерно равную 300/(3,142*√3) ≈ 300/(3,142*1,732) ≈ 300/5,442 ≈ 55,127 см.

Видео по теме

Источники:

• сторона шестиугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Шестиугольная шестиугольная форма появляется в некоторых неожиданных местах: ячейки сот, формы, которые мыльные пузыри образуют, когда они разбиваются вместе, внешний край болтов и даже шестигранные базальтовые колонны Дорожки Гиганта, природные скальные образования на северном побережье Ирландии. Предполагая, что вы имеете дело с обычным шестиугольником, а это означает, что все его стороны имеют одинаковую длину, вы можете использовать периметр шестиугольника или его площадь, чтобы найти длину его сторон.

TL; DR (слишком долго; не читал)

Самый простой и, безусловно, наиболее распространенный способ определения длины сторон правильного шестиугольника заключается в использовании следующей формулы:

s = P ÷ 6, где P – периметр шестиугольника, а s – длина любой из его сторон.

Расчет сторон шестиугольника от периметра

Поскольку обычный шестиугольник имеет шесть сторон одинаковой длины, найти длину любой из этих сторон так же просто, как разделить периметр шестиугольника на 6. Так что, если ваш шестиугольник имеет периметр 48 дюймов, у вас есть:

48 дюймов ÷ 6 = 8 дюймов.

Каждая сторона вашего шестиугольника имеет длину 8 дюймов.

Расчет сторон шестиугольника от области

Точно так же, как квадраты, треугольники, круги и другие геометрические фигуры, с которыми вы могли иметь дело, есть стандартная формула для расчета площади правильного шестиугольника. Это:

A = (1.5 × √3) × s ², где A – площадь шестиугольника, а s – длина любой из его сторон.

Очевидно, что вы можете использовать длину сторон шестиугольника для расчета площади. Но если вы знаете площадь шестиугольника, вы можете использовать ту же формулу, чтобы найти длину его сторон. Рассмотрим шестиугольник площадью 128 в ²:

1. Подставляемая область в уравнение

Начнем с подстановки площади шестиугольника в уравнение:

128 = (1, 5 × √3) × s ²

2. Изолировать переменную

Первым шагом в решении для s является выделение его с одной стороны уравнения. В этом случае деление обеих частей уравнения на (1, 5 × √3) дает вам:

128 ÷ (1, 5 × √3) = с ²

Условно переменная идет в левой части уравнения, поэтому вы также можете записать это как:

s ² = 128 ÷ (1, 5 × √3)

3. Упростите термин справа

Упростите термин справа. Ваш учитель может позволить вам приблизить √3 к 1.732, в этом случае у вас будет:

s ² = 128 ÷ (1, 5 × 1, 732)

Что упрощает до:

с ² = 128 ÷ 2, 598

Что, в свою очередь, упрощает:

s ² = 49, 269

4. Возьмите квадратный корень обеих сторон

Вы можете, вероятно, сказать, что путем проверки s будет близко к 7 (потому что 7 ² = 49, что очень близко к уравнению, с которым вы имеете дело). Но, взяв квадратный корень с обеих сторон с помощью калькулятора, вы получите более точный ответ. Не забудьте также написать в своих единицах измерения:

√ s ² = √49.269 тогда становится:

s = 7, 019 дюймов

Правильный шестиугольник: свойства, формулы, площадь

Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.

Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.

Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?

Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.

Мы знаем, что площадь правильного треугольника: .

Тогда площадь правильного шестиугольника — в шесть раз больше.

, где — сторона правильного шестиугольника.

Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.

Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.

Ты нашел то, что искал? Поделись с друзьями!

. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .

. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

Сторона правильного шестиугольника. Калькулятор и формулы

Определить сторону правильного шестиугольника можно легко при помощи этого калькулятора. Просто заполните любую ячейку, введя известное вам значение, – и под калькулятором отобразятся значения всех недостающих величин, а также формулы их нахождения. Это удобная шпаргалка по геометрии, которую полезно всегда держать под рукой!

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Правильный шестиугольник и его свойства

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

Замечание

Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;

каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

Теорема

Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]

Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: (a=R) .

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны (120^circ) .

4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

Замечание

В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .

[spoiler title=”источники:”]

http://calcon.ru/storona-pravilnogo-shestiugolnika-kalkulyator-i-formuly/

http://shkolkovo.net/theory/77

[/spoiler]