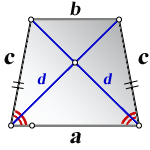
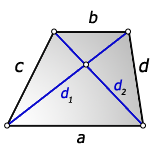
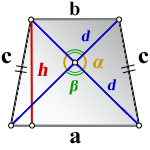
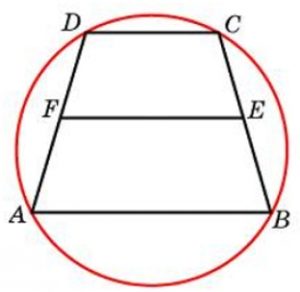
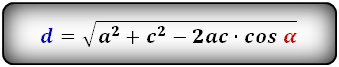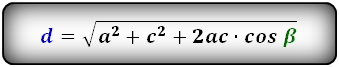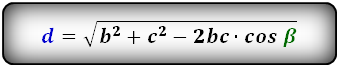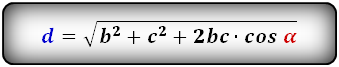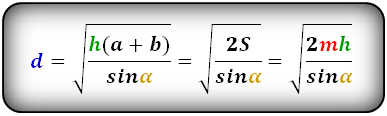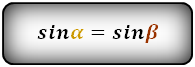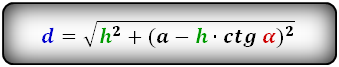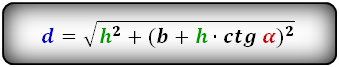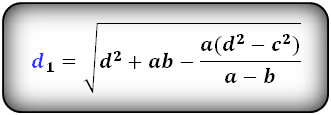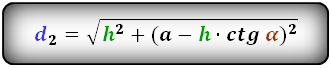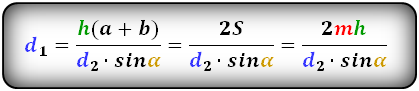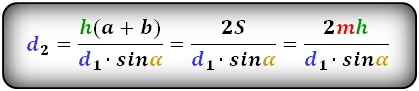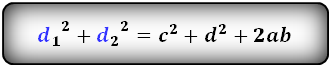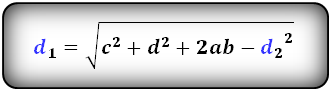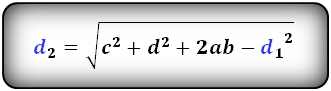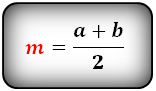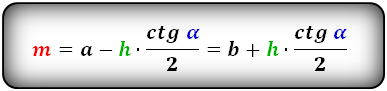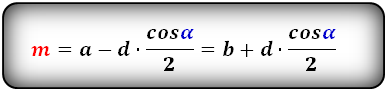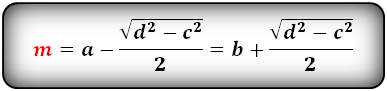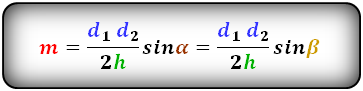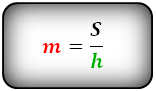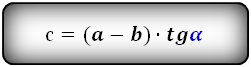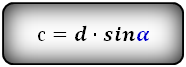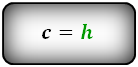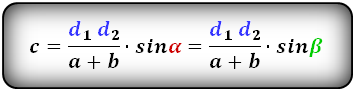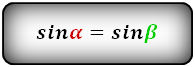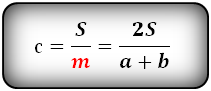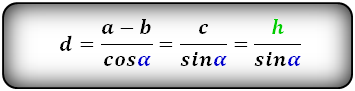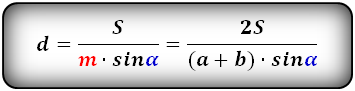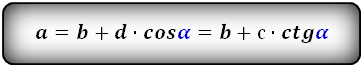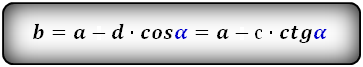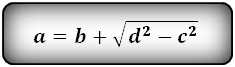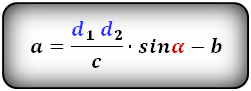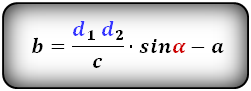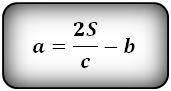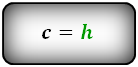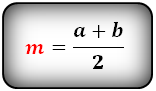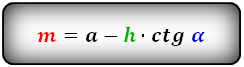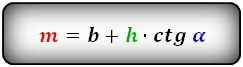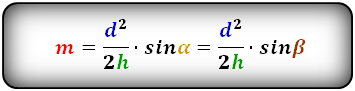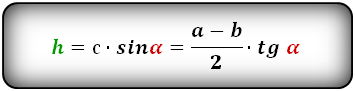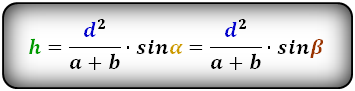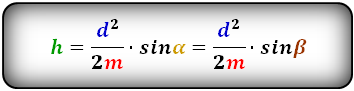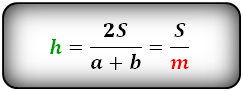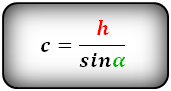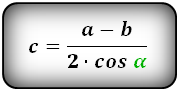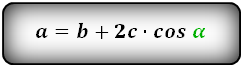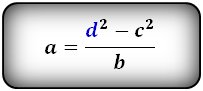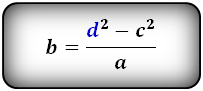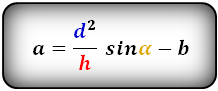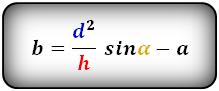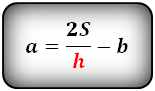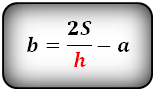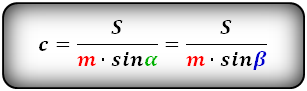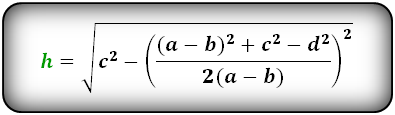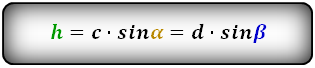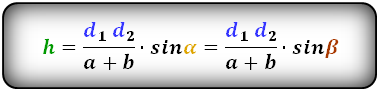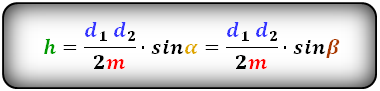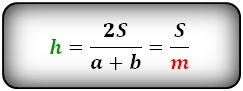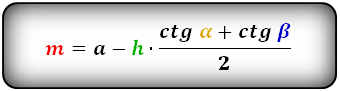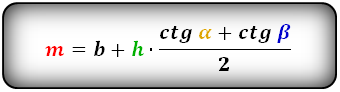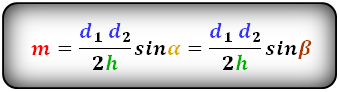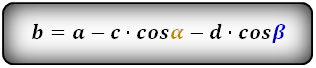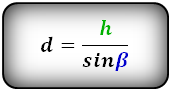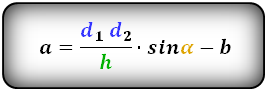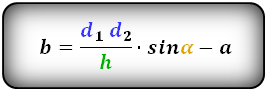1. Формулы длины диагонали равнобедренной трапеции через ее стороны
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагональ трапеции
Формула диагонали трапеции (d ):
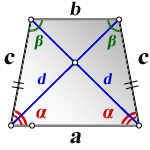
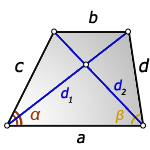
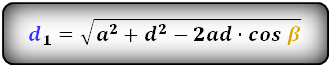
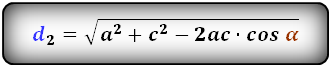
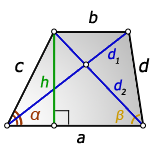
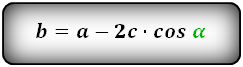
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α, β – углы трапеции
d – диагональ трапеции
Формулы диагонали трапеции (d ):
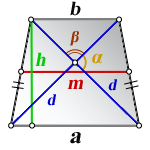
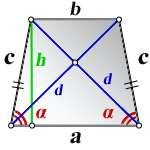
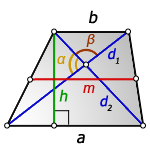
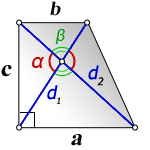
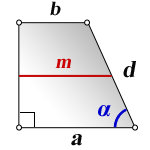
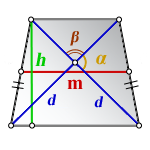
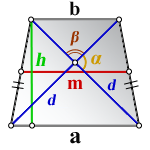
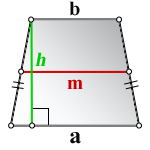
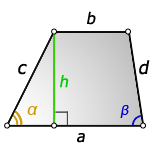
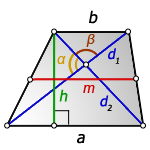
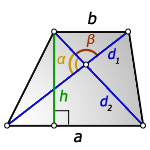
3. Формула длины диагонали равнобедренной трапеции
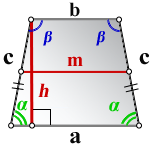
a – нижнее основание
b – верхнее основание
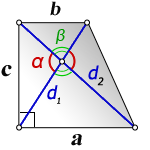
α, β – углы между диагоналями
h – высота трапеции
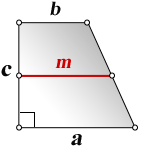
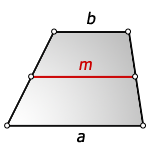
m – средняя линия трапеции
S – площадь трапеции
d – диагональ трапеции
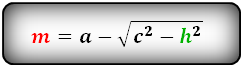
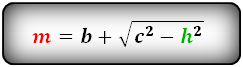
Формулы диагонали трапеции (d ):
Справедливо для данного случая :
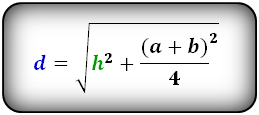
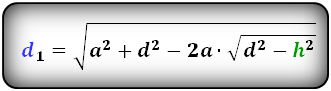
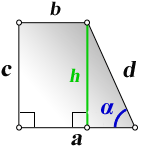
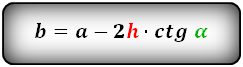
4. Формулы длины диагонали трапеции через высоту и стороны
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
h – высота трапеции
α – угол при нижнем основании
d – диагональ трапеции
Формулы диагонали трапеции (d ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2. Формула длины диагоналей трапеции через высоту
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
a – нижнее основание
b – верхнее основание
α, β – углы между диагоналями
h – высота трапеции
m – средняя линия трапеции
S – площадь трапеции
d1 , d2 – диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
d1 , d2 – диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
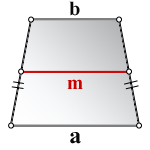
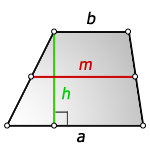
1. Формула средней линии трапеции через основания (для всех видов трапеции)
a – нижнее основание
b – верхнее основание
m – средняя линия
Формула средней линии, (m ):
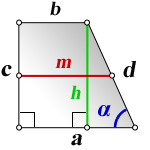
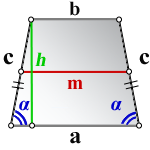
2. Формулы средней линии через основания, высоту и угол при нижнем основании
a, b – основания трапеции
c – боковая сторона под прямым углом к основаниям
d – боковая сторона
α – угол при основании
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
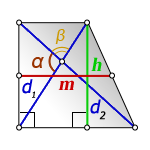
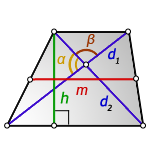
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
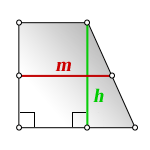
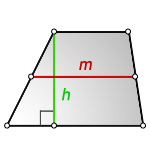
4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
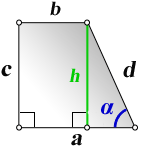
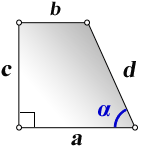
1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
a – нижнее основание
b – верхнее основание
d – боковая сторона
α – угол при нижнем основании
h – высота трапеции
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
a – нижнее основание
b – верхнее основание
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
c – боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
c – боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
α – угол при нижнем основании
h – высота трапеции
d – боковая сторона
Формулы длины боковой стороны (d) :
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
a – нижнее основание
b – верхнее основание
m – средняя линия трапеции
α – угол при нижнем основании
d – боковая сторона
Формула длины боковой стороны (d) :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины оснований прямоугольной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α – угол при нижнем основании
Формулы длины оснований :
3. Формулы длины оснований трапеции через диагонали и угол между ними
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
Формулы длины оснований :
4. Формулы длины оснований трапеции через площадь
a – нижнее основание
b – верхнее основание
c – боковая сторона под прямым углом к основаниям
h – высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
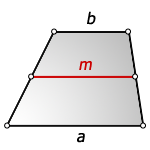
1. Формула средней линии равнобедренной трапеции через основания
a – нижнее основание
b – верхнее основание
m – средняя линия
Формула средней линии, (m ):
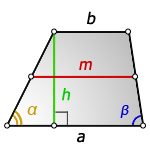
2. Формулы средней линии через основание, высоту и углы при нижнем основании
a – нижнее основание
b – верхнее основание
c – боковая сторона
α – угол при нижнем осровании
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S – площадь трапеции
h – высота трапеции
α – угол при нижнем осровании
m – средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
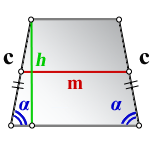
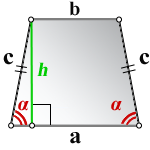
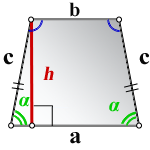
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при нижнем основании
h – высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
d – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
3. Формула высоты равнобедренной трапеции через площадь
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
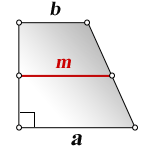
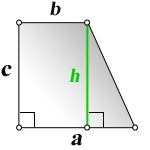
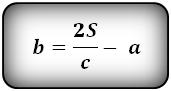
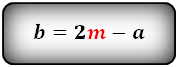
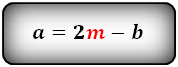
1. Формула длины основания равнобедренной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
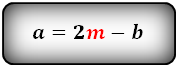
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
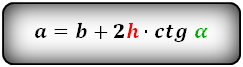
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
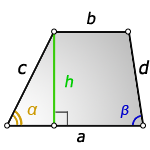
1. Формула высоты трапеции через стороны и углы при основании
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты трапеции через диагонали и углы между ними
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
3. Формула высоты трапеции через площадь
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
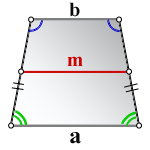
Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
b – верхнее основание
a – нижнее основание
m– средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
b – верхнее основание
a – нижнее основание
α, β – углы трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
α, β – углы между диагоналями
d1 , d2 – диагонали трапеции
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S – площадь трапеции
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции:
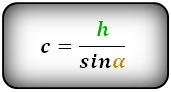
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
|
Пусть (displaystyle AD=73) и (displaystyle BC=43) – основания, (displaystyle AB=CD) – боковые стороны равнобедренной трапеции (displaystyle ABCDsmall.) По свойству равнобедренной трапеции углы при основании равны. Значит, (displaystyle cos angle A=cos angle D=frac{5}{7}small.) Требуется найти боковую сторону. Проведем высоты (displaystyle BH ) и (displaystyle CK ) трапеции. |
 |
Поскольку основания трапеции параллельны, а высоты трапеции перпендикулярны основаниям, (displaystyle BH K C ) – прямоугольник. Тогда (displaystyle H K =BC=43 small.)
|
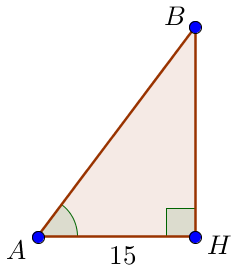
Прямоугольные треугольники (displaystyle ABH) и (displaystyle DCK) равны по гипотенузе (displaystyle AB=CD) и катету (displaystyle BH=CKsmall.) Значит (displaystyle AH=DK) и (displaystyle AH=DK=frac{AD-BC}{2}small,) (displaystyle AH=frac{73-43}{2}=frac{30}{2}=15small.) |
 |
|
Боковую сторону (displaystyle AB ) трапеции найдем из треугольника (displaystyle ABHsmall.) Нам известны (displaystyle cos angle BAH=frac{5}{7}) и прилежащий к острому углу (displaystyle BAH) катет (displaystyle AH=15small.) Так как (displaystyle cos angle BAH=frac{AH}{AB},) то (displaystyle AB=frac{AH}{cosangle BAH}=frac{15}{phantom{1}{displaystylefrac{5}{7}}phantom{1}}=) (displaystyle =frac{15cdot 7}{5}=3cdot 7=21small.) |
 |
Ответ: (displaystyle 21 small.)
ulerialeded519
Вопрос по геометрии:
В равнобедренной трапеции косинус острого угла равен 1/4, а основания равны 5 и9. Найдите боковую сторону трапеции. Помогите пожалуйста=)
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 2
touret591
Решение во вложении……………………..

pricoinouge242
ABCD – равнобедренная трапеция. ВН – высота. АН=(9-5)/2=2. Треуг-ник АНВ – прямоугольный. cosA=1/4. Косинус – это отношение прилежащего к углу катета к гипотенуе, т.е. АН/АВ=1/4, 2/АВ=1/4. Отсюда АВ=8.
Ответ: 8.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
|
Пусть (displaystyle AD=73) и (displaystyle BC=43) – основания, (displaystyle AB=CD) – боковые стороны равнобедренной трапеции (displaystyle ABCDsmall.) По свойству равнобедренной трапеции углы при основании равны. Значит, (displaystyle cos angle A=cos angle D=frac{5}{7}small.) Требуется найти боковую сторону. Проведем высоты (displaystyle BH ) и (displaystyle CK ) трапеции. |
 |
Поскольку основания трапеции параллельны, а высоты трапеции перпендикулярны основаниям, (displaystyle BH K C ) – прямоугольник. Тогда (displaystyle H K =BC=43 small.)
|
Прямоугольные треугольники (displaystyle ABH) и (displaystyle DCK) равны по гипотенузе (displaystyle AB=CD) и катету (displaystyle BH=CKsmall.) Значит (displaystyle AH=DK) и (displaystyle AH=DK=frac{AD-BC}{2}small,) (displaystyle AH=frac{73-43}{2}=frac{30}{2}=15small.) |
 |
|
Боковую сторону (displaystyle AB ) трапеции найдем из треугольника (displaystyle ABHsmall.) Нам известны (displaystyle cos angle BAH=frac{5}{7}) и прилежащий к острому углу (displaystyle BAH) катет (displaystyle AH=15small.) Так как (displaystyle cos angle BAH=frac{AH}{AB},) то (displaystyle AB=frac{AH}{cosangle BAH}=frac{15}{phantom{1}{displaystylefrac{5}{7}}phantom{1}}=) (displaystyle =frac{15cdot 7}{5}=3cdot 7=21small.) |
 |
Ответ: (displaystyle 21 small.)
Все формулы сторон трапеции
1. Формула длины основания трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
h – высота трапеции
Формулы всех четырех сторон трапеции :
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
d 1 , d 2 – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
Формулы трапеции
Для расчёта всех основных параметров трапеции воспользуйтесь калькулятором.
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
- Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме $$ FE = $$
- Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
- Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е. $$ KL = $$
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции
- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
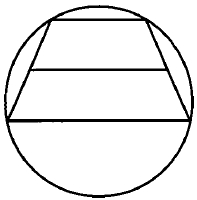
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции
Площадь трапеции через основания и высоту
Площадь трапеции через среднюю линию и высоту
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через четыре стороны
Формулы площади равнобедренной трапеции
Площадь трапеции через стороны
Площадь трапеции через стороны и угол
$$ S = AD * sin(∠ADC) * (DC – AD * cos(∠ADC)) $$ $$ S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC)) $$
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$ S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB) $$
Площадь трапеции если в нее вписана окружность
Формулы сторон произвольной трапеции
Основание через другое основание и среднюю линию
$$ AB = 2 * FE – DC $$ $$ DC = 2 * FE – AB $$
Основание через другое основание, диагонали и угол между ними
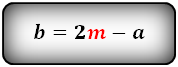
$$ DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ AB = DC – AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD) $$ $$ AB = DC – AD * cos(∠ADC) – BC * cos(∠BCD) $$ $$ AD = $$ $$ BC = $$
Формулы сторон равнобедренной трапеции
$$ AD = $$ $$ AD = $$ $$ DC = AB + 2 * AG * ctg(∠ADC) $$ $$ AB = DC – 2 * AG * ctg(∠ADC) $$ $$ DC = AB + 2 * AB * cos(∠ADC) $$ $$ AB = DC – 2 * AB * cos(∠ADC) $$
Длина основания через диагональ, боковую сторону и другое основание
Длина боковой стороны через диагональ и основания
Длина основания через высоту, другое основание, диагонали и угол между ними
Длина основания через высоту, другое основание и площадь трапеции
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
Длина боковой стороны через площадь трапеции, основания и угол при основании
Формулы сторон прямоугольной трапеции
$$ DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD) $$ $$ AB = DC – BC * cos(∠BCD) = DC – AD * ctg(∠BCD) $$ $$ DC = AB + sqrt $$ $$ AB = DC – sqrt $$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG) $$ DC = <2 * S over AD>- AB $$ $$ AB = <2 * S over AD>- DC $$
Формулы диагоналей произвольной трапеции
Длина диагоналей через четыре стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту
Длина диагоналей через стороны и другую диагональ
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
Формулы диагоналей равнобедренной трапеции
Длина диагоналей через стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту основание и угол при основании
Длина диагоналей через сторону и высоту
Формулы диагоналей прямоугольной трапеции
Формулы средней линии произвольной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и высоту
Формулы средней линии равнобедренной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
$$ FE = DC – AG * ctg(∠ADC) = AB + AG * ctg(∠ADC) $$
Длина средней линии через основания, боковую сторону и высоту
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и боковую сторону
Формулы средней линии прямоугольной трапеции
Длина средней линии через основания, высоту и угол при нижнем основании
Длина средней линии через основания, боковую сторону и угол при нижнем основании
Длина средней линии через основания и боковые стороны
Длина средней линии через диагонали, высоту и угол между диагоналями
Формулы высоты произвольной трапеции
Длина высоты через четыре стороны
Длина высоты через боковую сторону и прилегающий угол к основанию
$$ AG = AD * sin(∠ADC) = BC * sin(∠BCD) $$
Длина высоты через диагонали и углы между ними
Длина высоты через среднюю линию, диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы высоты равнобедренной трапеции
Длина высоты через по сторонам
Длина высоты через боковую сторону и прилегающий угол к основанию
Длина высоты через основания и прилегающий угол к основанию
Длина высоты через диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы боковых сторон прямоугольной трапеции
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
Сторона BC через основания и угол ∠BCD
Сторона BC через Сторону AD
Сторона BC через площадь, среднюю линию и угол ∠BCD
Сторона BC через площадь, основания и угол ∠BCD
Решение №2462 Около трапеции описана окружность. Периметр трапеции равен 38 …
Около трапеции описана окружность. Периметр трапеции равен 38, средняя линия равна 11. Найдите боковую сторону трапеции.
Источник: Ященко ЕГЭ 2022 (36 вар)
Средняя линия трапеции равна полусумме её оснований:
DC + AB = 2·11 = 22
Зная периметр, найдём сумму боковых сторон:
DA + CD = PABCD – (DC + AB) = 38 – 22 = 16
В окружность можно вписать только равнобедренную трапецию:
DA = CD = 16/2 = 8
[spoiler title=”источники:”]
http://calc-online24.ru/formula/trapez
[/spoiler]