Как найти сторону треугольника если известны вершины

Уравнения сторон треугольника

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

Таким образом, уравнение стороны AB

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

Отсюда уравнение стороны BC —

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

Как найти уравнения сторон треугольника если известны его вершины

Стороны треугольника заданы уравнениями:

Найти координаты вершин треугольника.

Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:

Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем

Вершина A имеет координаты

Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:

получаем .

Координаты вершины C получим, решая систему из уравнений сторон BC и AC:

Вершина C имеет координаты .

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Пример 1:

Построить треугольник, вершины которого находятся в точках А (2; 4), В (-3; 2), С (-3; -4). Найти:

1) уравнения сторон треугольника АВС;

2) координаты точки пересечения медиан;

3) длину и уравнение высоты, опущенной из вершины А;

4) площадь треугольника.

Решение от преподавателя:

Уравнение, прямой проходящей через две точки
1) Уравнения сторон треугольника АВС

2) Координаты точки пересечения медиан

Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Координаты т. E как середины отрезка ВС.

Уравнение АЕ

Координаты т. К как середины отрезка АВ.

Уравнение СК

3) Длина и уравнение высоты, опущенной из вершины А

Расстояние от точки до прямой

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

Уравнение AN

4) Площадь треугольника

Длина ВС

Пример 2:

Решение от преподавателя:

Пример 3:

По координатам вершин треугольника ABC найти:

• периметр треугольника;
• уравнения сторон AB и BC;
• уравнение высоты AD; угол ABC;
• площадь треугольника.

Сделать чертеж.

А(1; 2); В (–1; 2); С(3; 0).

Решение от преподавателя:

Пример 4:

Даны координаты вершин треугольникаА, В, С.

Требуется найти:

1) уравнение и длину стороны ВС;

2) уравнение и длину высоты, проведённой из вершиныА;

3) уравнение медианы, проведённой из вершиныА;

4) площадь треугольника.

Сделать чертёж.

А(4;-3), B(-2;-1), C(3;-2).

Решение от преподавателя:

Пример 5:

Решение от преподавателя:

1)

2)

3) Находим координаты точки М – середины стороны ВС:

       

Определяем длину медианы АМ:

4) Составляем уравнение медианы – прямой АМ:

5) Если ВН – высота, проведенная из вершины В к стороне АС, то, поскольку ВН проходит через точку В перпендикулярно вектору , то составляем уравнение высоты по формуле , где (a,b) – координаты вектора перпендикулярного искомой прямой,  – координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:

и подставляем в формулу, ,

6) Длину высоты ВН находим как расстояние от точки В до прямой АС:

7) Площадь треугольника АВС:

8) Находим угол ВАС треугольника:

9) Составляем уравнение прямой, проходящей через т.А параллельно ВС:

Ответ:

Пример 6:

Решение от преподавателя:

1. Уравнение прямой 
   Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 
   
   Уравнение прямой AB 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-3/₇x + ¹⁶/₇ или 7y + 3x – 16 = 0 
2. Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 
   
   
   M(3;1) 
   Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-8;2) и М(3;1), поэтому: 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-1/₁₁x + ¹⁴/₁₁ или 11y + x – 14 = 0 
3. Уравнение высоты через вершину C 
   Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
   
   Найдем уравнение высоты через вершину C 
   
   y = ⁷/₃x + ⁶²/₃ или 3y -7x – 62 = 0
4. уравнение параллельной прямой AB, проходящей через точку (-8,2)
   Уравнение прямой AB: y = ^-3/₇x + ¹⁶/₇
   Уравнение KN параллельно AB находится по формуле:
   y – y₀ = k(x – x₀)
   Подставляя x₀ = -8, k = ^-3/₇, y₀ = 2 получим:
   y-2 = ^-3/₇(x-(-8))
   или
   y = ^-3/₇x – ¹⁰/₇ или 7y + 3x +10 = 0

Пример 7:

Даны координаты вершин треугольника: A(1,1), B(4,13), C(10,5). 

Решение от преподавателя:

4) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-1/₄x + ¹⁵/₂ или 4y +x -30 = 0 
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k₁ прямой AB. 
Уравнение AB: y = 4x -3, т.е. k₁ = 4 
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k₁*k = -1. 
Подставляя вместо k₁ угловой коэффициент данной прямой, получим: 
4k = -1, откуда k = ^-1/₄ 
Так как перпендикуляр проходит через точку C(10,5) и имеет k = ^-1/₄,то будем искать его уравнение в виде: y-y₀ = k(x-x₀). 
Подставляя x₀ = 10, k = ^-1/₄, y₀ = 5 получим: 
y-5 = ^-1/₄(x-10) 
или 
y = ^-1/₄x + ¹⁵/₂ или 4y + x – 30 = 0 
Найдем точку пересечения с прямой AB: 
Имеем систему из двух уравнений: 
y -4x +3 = 0 
4y + x – 30 = 0 
Из первого уравнения выражаем y и подставим во второе уравнение. 
Получаем: 
x = ⁴²/₁₇ 
y = ¹¹⁷/₁₇ 
D(⁴²/₁₇;¹¹⁷/₁₇) 
Длина высоты треугольника, проведенной из вершины C 
Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + С = 0 равно абсолютному значению величины: 

Найдем расстояние между точкой C(10;5) и прямой AB (y -4x +3 = 0) 

5,7) Уравнение медианы треугольника 
Обозначим середину стороны BC буквой Е. Тогда координаты точки Е найдем по формулам деления отрезка пополам. 


Е(7;9) 
Уравнение медианы AЕ найдем, используя формулу для уравнения прямой, проходящей через две заданные точки A(1;1) иЕ(7;9), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁴/₃x ^-1/₃ или 3y -4x +1 = 0 
Найдем длину медианы. 
Расстояние между двумя точками выражается через координаты формулой: 

6) CD–диаметр окружности. Центр окружности точка О лежит в середине отрезка CD

Уравнение окружности  (x-x₀)²+(y-y₀)²=r²

(x-106/17)²+(y-101/17)²=256/17 

8) Уравнение прямой, параллельной CD, проходящей через точку A 

Пример 8:

Решение от преподавателя:

Точка D – середина стороны АВ , ее координаты равны полусумме координат А и В. Получим D(1, -1)

Пример 9:

Даны координаты вершин треугольника АВС: А (3,-2), В (-5,-4),  С (-1,6).

Найдите: 1) уравнения сторон треугольника АВ, ВС и АС;

2) периметр (сумму длин) треугольника;

3) уравнение высоты СН;

4) расстояние d от точки С до прямой АВ;

5) сделайте чертеж.

Решение от преподавателя:

Решение.

1) уравнения сторон треугольника АВ, ВС и АС

Уравнение, прямой проходящей через две точки

2) периметр (сумму длин) треугольника

Расстояние между двумя точками

3) уравнение высоты СН

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

4) расстояние d от точки С до прямой АВ

Расстояние от точки до прямой

Пример 10:

Даны вершины A (x₁; y₁), B (x₂; y₂), C (x₃; y₃)    треугольника.

Найти: 1) уравнение стороны AB;

2) уравнение медианы, проведенной из вершины C;

3) уравнение высоты, проведенной из вершины C ;

4) уравнение прямой, проходящей через вершину C параллельно стороне AB .

A (6; 0), B (2; − 6), C (−3; −9).

Решение от преподавателя:

Пример 11:

Решение от преподавателя:

Пример 12:

Дан треугольник  с координатами вершин найти:

а) длину стороны AB;

б) косинус угла ABC;

в) площадь треугольника ABC (через векторное произведение);

Решение от преподавателя:

Пример 13:

Решение от преподавателя:

Даны координаты вершин треугольника: A(6,0), B(2,-6), C(-3,-9). 
1) Уравнение прямой 
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 

Уравнение прямой AB 
Каноническое уравнение прямой: 

или 

или 
y = ³/₂x -9 или 2y -3x +18 = 0 

2) Уравнение медианы треугольника 
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(4;-3) 
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-3;-9) и М(4;-3), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁶/₇x ^-45/₇ или 7y -6x +45 = 0 
3) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-2/₃x -11 или 3y +2x + 33 = 0 
4) Уравнение прямой, параллельной AB, проходящей через С(-3,-9) 
Уравнение прямой AB: 2y -3x +18 = 0 
Уравнение СN параллельно AB находится по формуле: 

Или     2y -3x +9 = 0 

Пример 14:

Даны вершины треугольника А(8,1), В(0,3), С(-2,-3). Напишите уравнения стороны AB, медианы AD, высоты BE.

Решение от преподавателя:

Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(-1;0) 
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(8;1) и М(-1;0), поэтому: 

или 

или 
y = ¹/₉x + ¹/₉ или 9y -x – 1 = 0 
3) Уравнение высоты через вершину B

Пример 15:

Дан треугольник АВС. Найти:

а) величину угла А;

б) уравнение стороны АС;

в) уравнение высоты и медианы, опущенных из вершины В.

Сделать чертеж.

А(-1,2); В(1,3); С(3,-4).

Решение от преподавателя:

Пример 16:

Треугольник задан вершинами А(-6; -2);  В(4; 8); С(2; -8). Найти:

а) уравнение прямой BN, параллельной  стороне АС;

б) уравнение медианы CD;

в) уравнение высоты АЕ;

Решение от преподавателя:

а) уравнение прямой BN, параллельной  стороне АС;

Уравнение прямой AC:

Каноническое уравнение прямой:

или

или
y = ^-3/₄x ^-13/₂ или 4y + 3x +26 = 0

Уравнение BN параллельно AC находится по формуле:
y – y₀ = k(x – x₀)
Подставляя x₀ = 4, k = ^-3/₄, y₀ = 8 получим:
y-8 = ^-3/₄(x-4)
или
y = ^-3/₄x + 11 или 4y + 3x – 44 = 0

б) уравнение медианы CD;

Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.


M(-1;3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(2;-8) и М(-1;3), поэтому:
Каноническое уравнение прямой:

или

или
y = ^-11/₃x ^-2/₃ или 3y + 11x +2 = 0

в) уравнение высоты АЕ;

Прямая, проходящая через точку Е₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:

Найдем уравнение высоты через вершину A

y = ^-1/₈x – ¹¹/₄ или 8y +x + 22 = 0

Пример 17:

A(1, 2), В(5, 8), С(11, 3).

Решение от преподавателя:

Пример 18:

В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1).

Составить уравнения стороны (AB), высоты (ВК)  и медианы (CМ).

Решение от преподавателя:

Уравнение прямой AB
Каноническое уравнение прямой:

или

или
x +4 = 0 или x = -4
Уравнение прямой AC
Каноническое уравнение прямой:

или

или
y = ^-1/₄x + 3 или 4y + x – 12 = 0

Найдем уравнение высоты через вершину B

y = 4x + 13 или y -4x – 13 = 0

Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(8;1) и М(-4;¹/₂), поэтому:
Каноническое уравнение прямой:

или

или
y = ¹/₂₄x + ²/₃ или 24y -x – 16 = 0

Пример 19:

Дан треугольник ABC с координатами вершин A(-5;-3; 2), B(-2;-6;-3) и C(-2; 2;-1).
Найти:
а) длину стороны АВ;
б) косинус угла ABC;
в) площадь треугольника АВС (через векторное произведение).

Решение от преподавателя:

Как по координатам вершин треугольника найти уравнения его сторон

В аналитической геометрии треугольник на плоскости можно задать в декартовой системе координат. Зная координаты вершин, вы можете составить уравнения сторон треугольника. Это будут уравнения трех прямых, которые, пересекаясь, образуют фигуру.

Вам понадобится

• – ручка;
• – бумага для записей;
• – калькулятор.

Инструкция

Прямая на плоскости описывается уравнением: ax+bу+с = 0, где х,y – координаты по оси 0х и оси 0у какой-либо точки прямой; a, b, с – числовые коэффициенты. Причем a и b не могут равняться нулю одновременно. Такой вид записи называется общим уравнением прямой.

Также прямую можно задать выражением вида: y = kx+c. Это уравнение прямой с угловым коэффициентом k, который является тангенсом угла, образующегося при пересечении данной прямой с осью 0х.

Зная координаты двух точек А (х1;y1), В (х2;у2), вы можете записать уравнение прямой, проведенной через эти точки, используя пропорцию: (у-у1)/(у1-у2)=(х-х1)/(у1-у2). Далее, преобразовав это равенство, приведите его к виду как в шаге 1 или 2.

Рассмотрите алгоритм решения задачи на конкретном примере. Даны три вершины треугольника с известными координатами: А (9;8), В (7;-6), С (-7;4). Напишите уравнение прямых, образующих его.

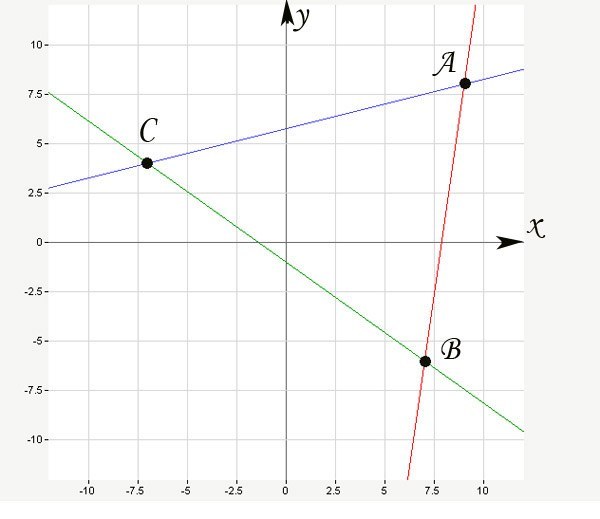
Найдите уравнение для прямой АВ. Примените формулу из шага 3, подставив значения координат точек А и В: (у-8)/(8-(-6)) = (х-9)/(9-7). Преобразуйте его: (у-8)/14 = (х-9)/2 или 2(у-8) = 14(х-9). Сократите уравнение, разделив левую и правую части на два, и раскройте скобки: у = 7х-63+8 = 7х-55.
Уравнение для АВ: у = 7х-55. Или: 7х-у-55 = 0 (АВ).

Аналогично напишите уравнение для прямой ВС: (у-(-6))/(-6-4) = (х-7)/7-(-7)). (у+6)/(-10) = (х-7)/14. 7(у+6) = -5(х-7). 7у+42 = -5х+35. 7у = -5х-7. у = -5/7х-1.
Уравнение для ВС: y = -5/7х-1. Или: -5х-7у-7 = 0 (ВС).

Затем уравнение для прямой СА: (у-8)/(8-4) = (х-9)/(9-(-7)). 16(у-8) = 4(х-9). 4у-32 = х-9. 4у = х-9+32. у = 0,25х+5,75.
Уравнение для СА: у = 0,25х+5,75. Или: х-4у+23 = 0 (СА).

Вы составили уравнения трех сторон фигуры. Для самопроверки постройте треугольника в системе координат. Найдите на чертеже значения пересечений прямых с осью 0у. Сравните эти координаты с полученными в уравнении. Например, для (BC) при y = 0, х = -1,4.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?