Как найти сторону треугольника когда известна биссектриса - Сайт, где вы сможете решить свои вопросы

Биссектриса равностороннего треугольника найти сторону

Задание 9. Биссектриса равностороннего треугольника равна 12√3. Найдите его сторону.

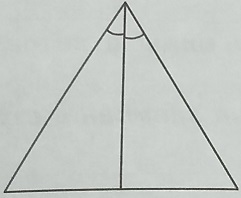
В равностороннем треугольнике все стороны равны, а биссектриса является также медианой и высотой h (см. рисунок).

Из рисунка видно, что сторону равностороннего треугольника можно найти из прямоугольного треугольника, в котором один катет является высотой h, второй – половина основания, равная a/2, к которому проведена высота, а роль гипотенузы будет играть сторона треугольника, равная a. Таким образом, по теореме Пифагора, можно записать равенство:

откуда выразим сторону треугольника:

Подставим вместо h=12√3, получим квадрат стороны треугольника:

и сторона равна

Задание 10. В треугольнике ABC известно, что AC = 7, BC = 24, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.

Радиус описанной окружности вокруг прямоугольного треугольника лежит в центре его гипотенузы. В задаче даны катеты прямоугольного треугольника с длинами 7 и 24 соответственно. По теореме Пифагора найдем длину гипотенузы, получим:

Таким образом, радиус описанной окружности равен

Свойства биссектрисы равностороннего треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.

Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.

Свойства биссектрисы равностороннего треугольника

Свойство 1

Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.

BD – биссектриса угла ABC, которая также является:

высотой, опущенной на сторону AC;
медианой, делящей сторону AC на два равных отрезка (AD = DC);

Свойство 2

Все три биссектрисы равностороннего треугольника равны между собой.

Свойство 3

Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.

Свойство 4

Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.

r – радиус вписанной окружности;
R – радиус описанной окружности;
R = 2r.

Свойство 5

Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.

Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.

Свойство 6

Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.

AD и AE – внешние биссектрисы, параллельные BC;
BK и BL – внешние биссектрисы, параллельные AC;
CM и CN – внешние биссектрисы, параллельные AB.

Свойство 7

Длину биссектрисы ( l_a ) равностороннего треугольника можно выразить через его сторону.

где a – сторона треугольника.

Пример задачи

Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.

Решение

Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).

Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):

Решение №2224 Биссектриса равностороннего треугольника равна 17√3. Найдите сторону этого треугольника.

Биссектриса равностороннего треугольника равна 17√3. Найдите сторону этого треугольника.

Источник: ОГЭ Ященко 2022 (50 вариантов)

В равностороннем треугольнике все углы равны 60°, а биссектриса является так же высотой.

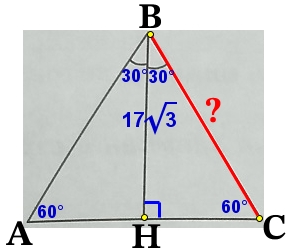
∠АВН = ∠СВН = 60°/2 = 30°
∠ВНС = 90°

В прямоугольном треугольнике ΔНВС, через косинус угла ∠СВН найдём искомую сторону ВС .
Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.

|:√3

ВС = 2·17 = 34

[spoiler title=”источники:”]

Свойства биссектрисы равностороннего треугольника

Решение №2224 Биссектриса равностороннего треугольника равна 17√3. Найдите сторону этого треугольника.

[/spoiler]

Источник

Объясните как находить сторону равностороннего треугольника, если известна биссектриса.

Ученик

(110),
на голосовании

7 лет назад

Голосование за лучший ответ

Лира

Мудрец

(12803)

7 лет назад

Биссектриса одновременно является высотой и медианой, углы равностороннего треугольника равны 60 градусам. Рассматривая треугольник, образованный биссектрисой, одной из сторон исходного треугольника и половиной стороны исходного (биссектриса является и медианой), получаем, что этот треугольник прямоугольный (биссектриса является и высотой) с углами 60 и 30 градусов. Отсюда и находим искомое.

Источник

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a, b, c – стороны произвольного треугольника

α, β, γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), (a):

Есть следующие формулы для определения катета или гипотенузы

a, b – катеты

c – гипотенуза

α, β – острые углы

Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):

Формулы сторон по теореме Пифагора, (a,b):

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b):

Формулы длины равных сторон , (a):

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β, γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, (H):

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через стороны и радиус, (H):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла

a, b – катеты

с – гипотенуза

c₁, c₂ – отрезки полученные от деления гипотенузы, высотой

α, β – углы при гипотенузе

Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

L– биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b – стороны треугольника

с – сторона на которую опущена биссектриса

d, e – отрезки полученные делением биссектрисы

γ – угол ABC , разделенный биссектрисой пополам

p – полупериметр, p=(a+b+c)/2

Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b – катеты прямоугольного треугольника

с – гипотенуза

α – угол прилежащий к гипотенузе

Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L – биссектриса, отрезок ME , исходящий из острого угла

a, b – катеты прямоугольного треугольника

с – гипотенуза

α, β – углы прилежащие к гипотенузе

Формулы длины биссектрисы через катет и угол, (L):

Формула длины биссектрисы через катет и гипотенузу, (L):

L – высота = биссектриса = медиана

a – одинаковые стороны треугольника

b – основание

α – равные углы при основании

β – угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

Формула высоты, биссектрисы и медианы, через стороны, (L):

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L – высота=биссектриса=медиана

a – сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M – медиана, отрезок |AO|

c – сторона на которую ложится медиана

a, b – стороны треугольника

γ – угол CAB

Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.

Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана

R – радиус описанной окружности

O – центр описанной окружности

с – гипотенуза

a, b – катеты

α – острый угол CAB

Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Источник

Нам необходимо найти длину стороны равностороннего треугольника.

Для решения:

рассмотрим теорию; выразим итоговую формулу; найдем длину стороны равностороннего треугольника.

Так как наш рассматриваемый треугольник является равносторонним следовательно мы можем утверждать, что длины всех его сторон будет соответственно равны. Обозначим длину стороны рассматриваемого треугольника как a.

Рассмотрим немного теории и выразим формулу

Рассмотрим, что такое биссектриса.

Биссектрисой является луч, исходящий из вершины угла и делящий данный угол пополам.

Или как проще можно сказать, что: биссектриса – это крыса, бегает по углам, делит угол пополам.

Нам известно, что в равностороннем треугольнике все биссектрисы внутренних углов равны и соответственно являются одновременно высотой и медианой данного треугольника.

Так как биссектриса является высотой, следовательно она делит противолежащую сторону пополам и опускается на нее под прямым углом. Исходя из этого мы можем выразить высоту исходя из теоремы Пифагора. Высота является одним из катетов прямоугольного треугольника следовательно:

a² = (a/2) ² + h²

Выразим из данной формулы h и получим, что:

h² = a² – (a/2) ² = a² – a² / 4 = a² * 3/4

Тогда длина стороны данного равностороннего треугольника составит:

a² = h² * 4/3

Следовательно:

a = sqrt (h² * 4/3) = h * sqrt (4/3) = 2 * h / sqrt 3

Найдем длину стороны равностороннего треугольника

Для нахождения длины стороны равностороннего треугольника воспользуемся формулой (1) и получим, что:

a = h * 2 / (sqrt 3) = 9 sqrt 3 * 2 / sqrt 3 = 2 * 9 sqrt 3 / sqrt 3 = 2 * 9 = 18 см

Ответ: 18 см

Источник

Задача

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.

Найти стороны треугольника ABC.

Дано: ΔABC,

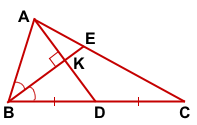
AD — медиана, BE — биссектриса,

AD=BE=8, AD⊥BE

Найти: AB, BC, AC

Решение:

1) Пусть AD∩BE=K.

Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD. Следовательно, BC=2AB.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

3) По свойству биссектрисы треугольника в ΔABC

$[ frac{{BC}}{{AB}} = frac{{CE}}{{AE}} = frac{2}{1}. ]$

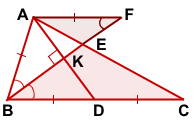
3) Проведём через точку A прямую, параллельную BC и продлим BE до пересечения с этой прямой в точке F.

Рассмотрим треугольники BEC и FEA.

∠AFB=∠CBF (как внутренние накрест лежащие при BC || AF и секущей BF).

∠BEC=∠FEA (как вертикальные).

Значит треугольники BEC и FEA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$[ frac{{BC}}{{FA}} = frac{{CE}}{{AE}} = frac{{BE}}{{FE}} = frac{2}{1}. ]$

$[ frac{{BC}}{{FA}} = frac{2}{1}, Rightarrow FA = frac{1}{2}BC = AB. ]$

Таким образом, треугольник ABF — равнобедренный с основанием BF, а значит, его высота AK является также медианой и BK=KF.

$[ frac{8}{{FE}} = frac{2}{1}, Rightarrow FE = 4, ]$

BF=BE+FE=12, BK=KF=6.

4) Рассмотрим прямоугольный треугольник ABK. По теореме Пифагора

$[ AB = sqrt {6^2 + 4^2 } = sqrt {52} = 2sqrt {13} , ]$

5) Рассмотрим прямоугольный треугольник AKE.

KE=BE-BK=8-6=2. По теореме Пифагора

$[ AE = sqrt {4^2 + 2^2 } = sqrt {20} = 2sqrt 5 , ]$

$[ frac{{CE}}{{AE}} = frac{2}{1}, Rightarrow CE = 2AE, ]$

Ответ:

II способ

1) Пусть AD∩BE=K.

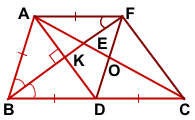
Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD.

Следовательно, BC=2AB.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

2) Отложим на луче BE с другой стороны от точки K отрезок KF, KF=BK.

Проведём отрезки DF и CF.

Четырёхугольники AFDB и AFCD — параллелограммы (по признаку параллелограмма). Тогда AF=BD, DF=AB, FC=AD (по свойству параллелограмма), а так как AB=BD, то ABCD — ромб.

AC∩DF=O. По свойству параллелограмма O — середина DF. Значит E — точка пересечения медиан треугольника AFD. По свойству медиан FE:EK=2:1. Следовательно

$[ EK = frac{1}{3}KF = frac{1}{3}BK,]$