Как найти сторону треугольника когда известна площадь

Ну или не совсем простая, но способов решений будет много. Ну и рисунок-подсказка должен натолкнуть на «продолжение»… Ну или запутать.

Задача в продолжение темы «метрическое соотношение сторон в треугольнике», поэтому стоит этот раз решить как раз схожим (с предыдущими задачами) способом. Но как сказано выше — способов тут не мало я перечислю несколько в подсказках, а Вы попробуйте найти свой.

Условие

Две стороны треугольника равны 2√2 и 3, площадь треугольника равна 3. Найдите третью сторону.

Подсказки

Начнём с оптимального (по теме прошлых задач) варианта решения — теорема косинусов. Да да. Но вот известного угла только между сторонами нет. Что делать? Вспоминать про площадь! Через площадь и две стороны можно узнать синус угла, а там и косинус через основное тригонометрическое тождество (если синус совсем неприглядный или узнать угол по табличному значению). Тут главное не ошибиться и не проморгать угол (острый или тупой).

Второй вариант, прям напрашивается из условия — теорема Геррона.

Третий способ, к которому многие (зачем-то?) прибегают — дополнительное построение высоты. Ну и «беспорядочное» использование теоремы Пифагора. Тут так тоже можно.

Последние два способа — не исключение. Надо внимательно следить за углами. Треугольник-то может быть как тупоугольным, так и…

#школьное образование #огэ по математике #егэ по математике #задачи по математике

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b – катеты, с – гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b – катеты, с – гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a – искомая сторона, S – площадь треугольника.

2) Найти сторону через высоту

где a – искомая сторона,h – высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a – искомая сторона,r – радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a – искомая сторона,R – радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a – искомая сторона, b – известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Как найти сторону треугольника по двум сторонам и площади?

Как найти площадь треугольника если известны две стороны?

Площадь треугольника через две стороны и угол между ними.

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

Как найти длину стороны треугольника?

c 2 = a 2 +b 2 , где a, b — катеты, с — гипотенуза прямоугольного треугольника. После того, как найдены все стороны треугольника, находим его периметр, как сумму двух катетов и гипотенузы.

Как найти третью сторону в равнобедренном треугольнике?

Зная боковую сторону равнобедренного треугольника и угол при основании, можно найти третью сторону. По аналогичному алгоритму можно найти сторону равнобедренного треугольника, зная высоту, но в таком случае половина основания будет равна произведению высоты на синус угла при основании.

Как найти синус угла зная две стороны?

Для этого воспользуйтесь соотношением, указанным ниже:a/sin α=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда известны две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.

[spoiler title=”источники:”]

http://www-formula.ru/2011-10-09-11-08-41

http://fcessentuki.ru/kak-naiti-storonu-treugolnika-po-dvum-storonam-i-ploshchadi

[/spoiler]

Как найти стороны прямоугольного треугольника, зная площадь

В прямоугольном треугольнике один угол прямой, другие два – острые. Сторона, противостоящая прямому углу, называется гипотенузой, другие две стороны – катеты. Зная площадь прямоугольного треугольника, можно вычислить стороны по известной формуле.

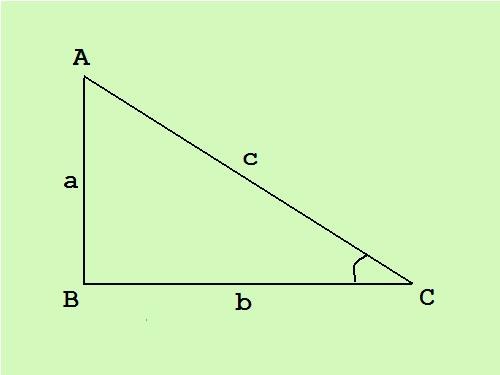
Инструкция

В прямоугольном треугольнике катеты перпендикулярны друг другу, следовательно, общая формула площади треугольника S = (c*h)/2 (где с – основание, а h – высота, проведенная к этому основанию) превращается в половину произведения длин катетов S = (a*b)/2.

Задача 1.
Найдите длины всех сторон прямоугольного треугольника, если известно, что длина одного катета превышает длину другого на 1 см, а площадь треугольника равна 28 см.

Решение.
Запишите основную формулу площади S = (a*b)/2 = 28. Известно, что b = a + 1, подставьте это значение в формулу: 28 = (a*(a+1))/2.
Раскройте скобки, получите квадратное уравнение с одной неизвестной a^2 + a – 56 = 0.
Найдите корни этого уравнения, для чего посчитайте дискриминант D = 1 + 224 = 225. Уравнение имеет два решения: a_1 = (-1 + √225)/2 = (-1 + 15)/2 = 7 и a_2 = (-1 – √225)/2 = (-1 – 15)/2 = -8.
Второй корень не имеет смысла, поскольку длина отрезка не может быть отрицательной величиной, так что a = 7 (см).
Найдите длину второго катета b = a + 1 = 8 (см).
Осталось найти длину третьей стороны. По теореме Пифагора для прямоугольного треугольника c^2 = a^2 + b^2 = 49 + 64, отсюда c = √(49 + 64) = √113 ≈ 10.6 (см).

Задача 2.
Найдите длины всех сторон прямоугольного треугольника, если известно, что его площадь равна 14 см, а угол ACB равен 30°.

Решение.
Запишите основную формулу S = (a*b)/2 = 14.
Теперь выразите длины катетов через произведение гипотенузы и тригонометрических функций по свойству прямоугольного треугольника:
a = c*cos(ACB) = c*cos(30°) = c*(√3/2) ≈ 0.87*c.
b = c*sin(ACB) = c*sin(30°) = c*(1/2) = 0.5*c.

Подставьте полученные значения в формулу площади:
14 = (0.87*0.5*c^2)/2, откуда:
28 ≈ 0.435*c^2 → c = √64.4 ≈ 8 (см).
Вы нашли длину гипотенузы, теперь найдите длины двух других сторон:
a = 0.87*c = 0.87*8 ≈ 7 (см), b = 0.5*c = 0.5*8 = 4 (см).

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?