Как найти сторону треугольника зная сторону квадрата

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Треугольник. Формулы определения и свойства треугольников.

В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры – треугольника. А также разберем некоторе примеры решения задач на треугольники.

Содержание:

Определение треугольника

Треугольник – это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом – △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)

• Точки A, B и C – вершины треугольника. Принято писать их большими буквами.
• Отрезки AB, BC и СА – стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
• Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b – β, с – γ.

Углы треугольника, также, можно обозначать специальным символом – ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:

Классификация треугольников

Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.

1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Свойства треугольника

1.Свойства углов и сторон треугольника.

• Сумма всех углов треугольника равна 180°:

• Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

• В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

2.Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c
sin α	sin β	sin γ

3. Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

4. Теорема о проекциях

Для остроугольного треугольника:

Медианы треугольника

Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

AO	=	BO	=	CO	=	2
OD	OE	OF	1

3. Медиана треугольника делит треугольник на две равновеликие по площади части

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны:

Как найти третью сторону треугольника — формулы и расчеты

В геометрии первая фигура, которую школьники начинают изучать, это треугольник. Он является одним из самых распространенных и простых замкнутых объектов. Знание свойств фигуры и необходимых теорем позволяет решать разные задачи о том, как найти третью сторону треугольника на плоскости.

Фигура из шести элементов

Под геометрическим элементом полагают какой-либо объект, который имеет определенную меру и является составляющей частью некоторой фигуры. Например, для сферы основными образующими элементами являются радиус и центр.

Как известно, треугольник — это фигура, которая состоит из трех отрезков и такого же количества вершин. При этом все отрезки попарно пересекаются. Из определения фигуры следует, что ее образуют два типа элементов, общее количество которых составляет 6:

• сторона (3);
• вершина (3).

Обычно треугольник обозначают большими латинскими буквами, например, ABC, PQM и так далее. Каждая буква — это название вершины (точка пересечения двух отрезков). AB, BC и CA, которые являются длинами сторон, принято обозначать маленькими латинскими буквами по названию противоположных им вершин, то есть c, a и b, соответственно.

Дополнительные отрезки

Несмотря на всю простоту построения фигуры, она обладает большим количеством дополнительных элементов, которые ее могут определять. Среди них самыми важными являются следующие:

Медиана — отрезок, который соединяет вершину и середину противоположной стороны. Таких отрезков в треугольнике три. Все они пересекаются в одной точке, которая является центром масс фигуры. Эта точка делит каждую медиану в отношении 2:1, начиная от вершины. Каждый из трех названных отрезков делит треугольник на две аналогичных фигуры равной площади.

Биссектриса — отрезок, который отличается от медианы тем, что он делит пополам соответствующий угол.

Высота — перпендикуляр, который из вершины опускается на сторону фигуры. Его удобно использовать при вычислении площади или при определении его углов через тригонометрические выражения. Для некоторых типов треугольников высота может совпадать со стороной (катет в прямоугольной фигуре).

Радиусы вписанной и описанной окружностей. Эти замкнутые симметричные кривые можно провести для любого треугольника. Указанные радиусы однозначно определяются через стороны и углы фигуры.

Средняя линия — это соединяющий две середины сторон отрезок. Его особенность заключается в том, что он всегда параллелен третьей стороне и равен половине ее длины.

Виды треугольников

Разработана достаточно развитая классификация рассматриваемых фигур. Главными ее пунктами являются значения углов треугольника и взаимоотношение между его отрезками. Так, если в фигуре все углы острые, то она называется остроугольной. Если же один из углов больше 90 °, то треугольник полагается тупоугольным. Чаще всего в задачах рассматривают следующие виды:

Основные свойства и понятия

Треугольник является одной из самых изученных фигур в геометрии. Для него известны многие теоремы, которые с успехом используются при решении задач. Существует два основных свойства фигуры, которые следуют из характеристик евклидового пространства:

Равенство суммы трех углов 180 °, то есть A + B + C = 180 °. Этот факт доказал еще Евклид в своем знаменитом труде «Элементы». По этой причине треугольник не может содержать больше одного прямого или тупого внутреннего угла.

Если известны три отрезка a, b и c такие, что выполняется равенство a + b = c, то из них составить треугольник невозможно. Это фундаментальное свойство говорит о том, что для всякого типа рассматриваемой фигуры сумма длин ее двух любых сторон всегда больше длины третьей.

Помимо названных свойств, следует знать о треугольнике еще такое понятие, как подобие. Его суть состоит в том, что одна из рассматриваемых фигур является точной копией в миниатюре другой. Для подобных треугольников все углы равны попарно, а все три стороны относятся соответственно попарно друг к другу с одним и тем же коэффициентом подобия.

Еще одной полезной характеристикой рассматриваемой фигуры является ее качество (CT). Вычисляется оно по следующей формуле:

CT = (a + b — c)*(b + c — a)*(c + a — b)/(a*b*c).

Величина CT лежит в пределах от 0 до 1. Она показывает степень близости фигуры к равностороннему, то есть к наиболее симметричному объекту. Если CT 0,5, то фигура характеризуется, как имеющая хорошее качество.

Величина CT применяется для алгоритмов, которые разделяют какую-либо изучаемую геометрическую поверхность на сетку треугольников. Если в этой сетке генерируется много низкокачественных фигур, то будет велика ошибка аппроксимации рассматриваемой величины.

Важные теоремы

Знание теорем для рассматриваемой фигуры позволяет понять, как найти сторону, зная 2 стороны треугольника. Прежде всего применяются две базовые теоремы:

Синусов. Как известно, синус — это тригонометрическая функция, которая вводится в прямоугольном треугольнике и определяет отношение противолежащего углу катета к гипотенузе. Теорема синусов для фигуры произвольного типа устанавливает следующее математическое взаимоотношение между отрезками и углами: a/sinA = b/sinB = c/sinC. Это означает, что вычислить длину любой стороны можно, если известен еще какой-нибудь отрезок и два угла.

Косинусов. Как и синус, косинус тоже является тригонометрической функцией, которая определяет отношение катета прилежащего к гипотенузе прямоугольной фигуры. Теорему косинусов удобно записать в виде следующего математического выражения: c 2 = a 2 + b 2 — 2*a*b*cosC. С помощью этого равенства можно найти 3 сторону треугольника по 2 сторонам известным и углу между ними.

К этим двум теоремам следует добавить еще два важных равенства, которые связаны с именами древнегреческих философов.

Первое выражение базируется на знаменитой теореме Пифагора, которая устанавливает связь между длинами двух катетов (меньшие стороны) и гипотенузы (большая сторона) в треугольнике с прямым углом. Если гипотенузу обозначить буквой c, тогда будет выполняться следующее равенство:

Если известные любые две стороны, то для определения третьей достаточно взять под квадратный корень соответствующую сумму или разницу квадратов.

Вторая из дополнительных теорем носит название философа Аполлония Пергского. Соответствующее ей математическое выражение выглядит так:

a 2 + b 2 = ½*c 2 + 2*Mc 2 .

Здесь Mc — это медиана, проведенная к стороне c из вершины C. Это равенство также называют в математике теоремой медианы.

Примеры решения задач

После того как изучены и рассмотрены основные понятия, свойства и теоремы для различного рода треугольников, можно переходить к решению геометрических задач. Поскольку для этого требуется в большинстве случаев знать значения тригонометрических функций, рекомендуется воспользоваться либо соответствующими таблицами, либо инженерным калькулятором.

Задачи школьного курса с треугольниками, как правило, не являются сложными. Они решаются благодаря однократному применению какого-либо свойства или теоремы.

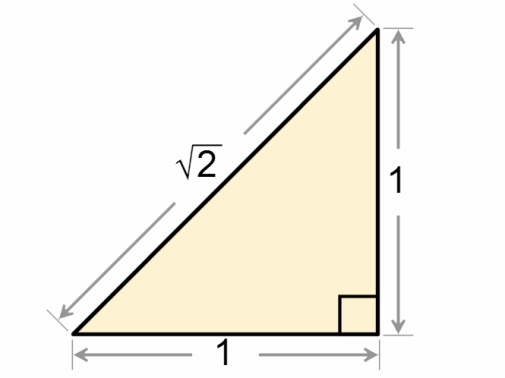
Квадрат и его диагональ

Пусть дан квадрат, сторона которого составляет 11 см. Необходимо определить половину длины его диагонали.

Эту геометрическую задачу проще всего решить, если увидеть, что две смежные стороны исходной фигуры и ее диагональ образуют прямоугольный треугольник, который к тому же является равнобедренным. Каждая из равных сторон в нем имеет длину 11 см и является катетом. Диагональ c — это гипотенуза. Применяя пифагорову теорему, можно получить следующее равенство:

c = (11 2 + 11 2 )^0,5 ≈ 15,556 см.

Поскольку половина диагонали в два раза меньше гипотенузы, то искомым ответом на задачу будет число c/2 ≈ 7,778 см.

Две высоты и угол

Дан треугольник ABC. Известно, что при вершине C угол составляет 37 °. Из вершин A и B проведены высоты к сторонам этого треугольника, их длины составляют h1 = 10 см и h2 = 8 см, соответственно. Необходимо узнать длину стороны фигуры, которая лежит против угла C.

Из условия задачи можно найти длины сторон AC и BC. Для этого следует увидеть, что каждая из высот с двумя другими сторонами треугольника образует прямоугольную фигуру. Воспользовавшись тригонометрическими равенствами, можно получить следующие результаты:

• AC = h1/sinC = 10/sin (37 °) ≈ 16,616 см;
• BC = h2/sinC = 8/sin (37 °) ≈ 13,293 см.

Против угла C лежит сторона AB, которую следует найти. Получается, что известны две стороны треугольника (AC и BC) и угол между ними. Остается применить теорему косинусов, чтобы получить ответ:

AB = (AC 2 + BC 2 — 2*AC*BC*cosC)^0,5 = (16,616 2 + 13,293 2 — 2* 16,616 * 13,293 *cos (37 °))^0,5 ≈ 10 см.

Полученный результат свидетельствует о том, что высота h1 совпадает со стороной AB с рассчитанной точностью, то есть исходный треугольник являлся прямоугольным.

Таким образом, для нахождения стороны треугольника, если известны две другие его стороны или иные отрезки, следует воспользоваться теоремами. Основными из них являются теорема косинусов и синусов, а также Пифагора и Аполлония.

[spoiler title=”источники:”]

http://binary2hex.ru/triangle.html

http://sprint-olympic.ru/uroki/geometrija/128034-kak-naiti-tretu-storony-treygolnika-formyly-i-raschety.html

[/spoiler]

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b – катеты, с – гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b – катеты, с – гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a – искомая сторона, S – площадь треугольника.

2) Найти сторону через высоту

где a – искомая сторона,h – высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a – искомая сторона,r – радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a – искомая сторона,R – радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a – искомая сторона, b – известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Формул для нахождения стороны треугольника не так уж много, но главное не знать их – а успешно применять при решении задач, ведь далеко не каждую задачу можно решить в лоб.

Сейчас на примере я покажу, как нужно их применять.

Есть произвольный треугольник со стороной 18 см, один угол при нем равен 30 градусам, а площадь равна 36 см.кв. Нужно найти две другие стороны. Сделаем рисунок

Для решения задачи проведем к основанию (с=18см) высоту h и тем самым разделим наш треугольник на два прямоугольных.

Исходя из формулы площади, найдем высоту

S = 1/2h*c откуда h = 2S/c = 2*36/18 = 4 см

Теперь находим сторону b по синусу угла

sin = h/b (отношение противоположного катета к гипотенузе) откуда b = h/(sin 30) = 4/(1/2) = 8 см.

Мы уже знаем две стороны у угол между ними и третью сторону можно найти по формуле из теоремы косинусов, но к сожалению не всегда мы ее помним. В нашем случае ничего страшного – найдем сторону а по формуле Пифагора, но для начала нам нужно найти сторону х.

Можно по формуле Пифагора

откуда х = квадратный корень из (8*8 – 4*4), что равно 4*(кв.к3)

и находим последнюю сторону нашего треугольника

а = кв.к из (c-x)*(c-x) + h*h = кв.к из 18*18-2*18*4*(кв.к3)+4*(кв.к3)*4*(кв.к3)+4*4

здесь стоит обратить внимание, что

18*18 = с*с

4*(кв.к3)*4*(кв.к3)+4*4 = 4*4*3+4*4 = 4*4*4 = 4*2*2*2 = 8*8 = b*b

2*18*4*(кв.к3) = 2*18*4*2*(кв.к3/2) = 2*18*8*(кв.к3/2) = 2*с*b*cos30 и теперь можно записать

а = кв.к из с*с – 2*с*b*cos30 + b*b Что на самом деле есть формулой нахождения стороны треугольника по теореме косинусов (мы ее только что вывели)

Теперь посчитаем и найдем сторону а = 11,772 см.

Как найти сторону квадратного треугольника

Квадратный треугольник более точно называется прямоугольным треугольником. Соотношения между сторонами и углами этой геометрической фигуры подробно рассматриваются в математической дисциплине тригонометрии.

Вам понадобится

• – лист бумаги;
• – ручка;
• – таблицы Брадиса;
• – калькулятор.

Инструкция

Найдите сторону прямоугольного треугольника с помощью теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: с2 = a2+b2 , где с – гипотенуза треугольника, a и b – его катеты. Чтобы применить это уравнение, нужно знать длину любых двух сторон прямоугольного треугольника.

Если по условиям заданы размеры катетов, отыщите длину гипотенузы. Для этого с помощью калькулятора извлеките квадратный корень из суммы катетов, каждый из которых предварительно возведите в квадрат.

Вычислите длину одного из катетов, если известны размеры гипотенузы и другого катета. При помощи калькулятора извлеките квадратный корень из разности гипотенузы в квадрате и известного катета, также возведенного в квадрат.

Если в задаче заданы гипотенуза и один из прилежащих к ней острых углов, используйте таблицы Брадиса. В них приведены значения тригонометрических функций для большого числа углов. Воспользуйтесь калькулятором с функциями синуса и косинуса, а также теоремами тригонометрии, которые описывают соотношения между сторонами и углами прямоугольного треугольника.

Найдите катеты при помощи основных тригонометрических функций: a = c*sin α, b = c*cos α, где а – катет, противолежащий к углу α, b – катет, прилежащий к углу α. Подобным образом посчитайте размер сторон треугольника, если заданы гипотенуза и другой острый угол: b = c*sin β, a = c*cos β, где b – катет, противолежащий к углу β, а – катет, прилежащий к углу β.

В случае, когда известен катет a и прилежащий к нему острый угол β, не забывайте, что в прямоугольном треугольнике сумма острых углов всегда равна 90°: α + β = 90°. Отыщите значение угла, противолежащего к катету а: α = 90° – β. Или воспользуйтесь тригонометрическими формулами приведения: sin α = sin (90° – β) = cos β; tg α = tg (90° – β) = ctg β = 1/tg β.

Если известен катет а и противолежащий к нему острый угол α, при помощи таблиц Брадиса, калькулятора и тригонометрических функций вычислите гипотенузу по формуле: c=a*sin α, катет: b=a*tg α.

Видео по теме

Источники:

• Как найти стороны прямоугольного треугольника по катету и острому углу

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.

Сторона равностороннего треугольника через радиус описанной окружности

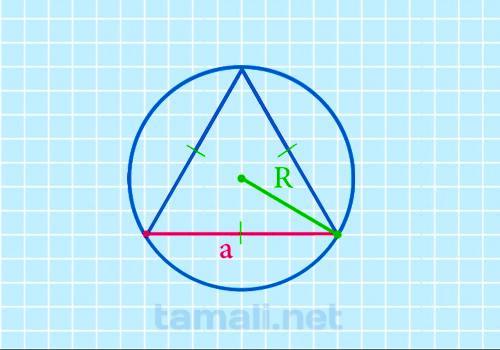
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:

a = R * √3

где а — сторона треугольника, R — радиус описанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.

Сторона равностороннего треугольника через радиус вписанной окружности

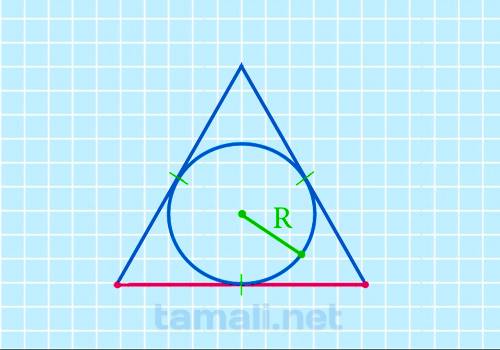
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):

a = 2r * √3

где а — сторона треугольника, R — радиус вписанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.

Сторона равностороннего треугольника через высоту

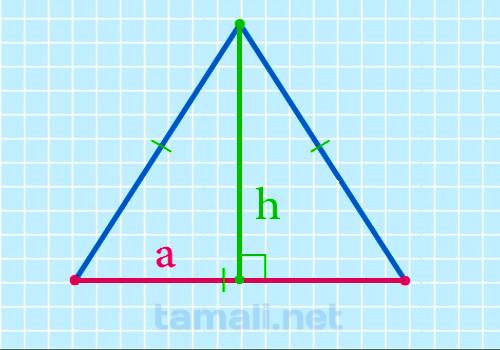
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:

a = 2h / √3

где а — сторона, h —  высота равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.

Сторона равностороннего треугольника через площадь

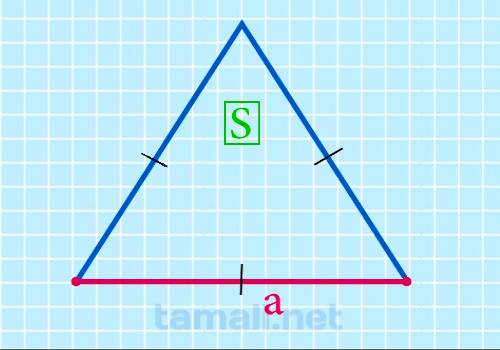
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу

a = √(4S / √3)

где а — сторона, S —  площадь равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.

Основание равнобедренного треугольника через боковые стороны и угол между ними

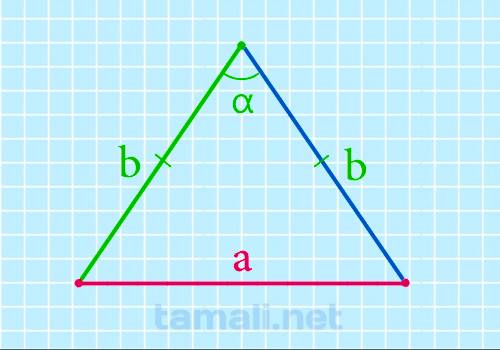
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:

a = 2b * sin (α/2)

где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.

Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.

Основание равнобедренного треугольника через боковые стороны и угол при основании

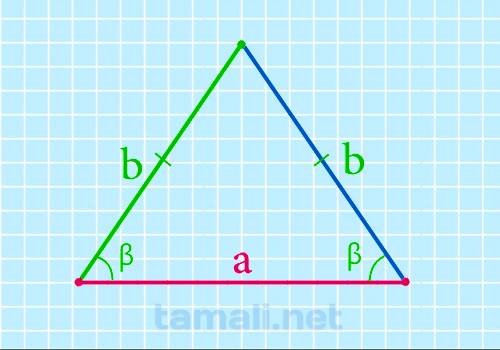
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:

a = 2b + cos β

где b — боковая сторона, β — угол при основании.

Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.

Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами

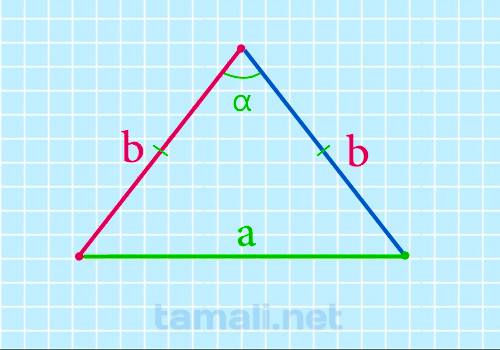
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным.  Это значит, что α = β.

Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:

b = a / (2 * sin(α/2))

где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.

Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.

Боковая сторона равнобедренного треугольника через основание и угол при основании

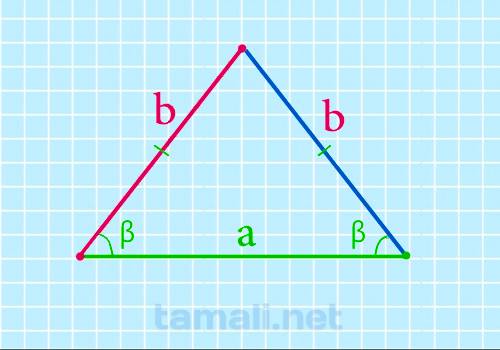
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:

b = a / 2 * cos β

где a — это основание, β — угол при основании равнобедренного треугольника.

Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.

Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.

Катет прямоугольного треугольника через гипотенузу и острый угол

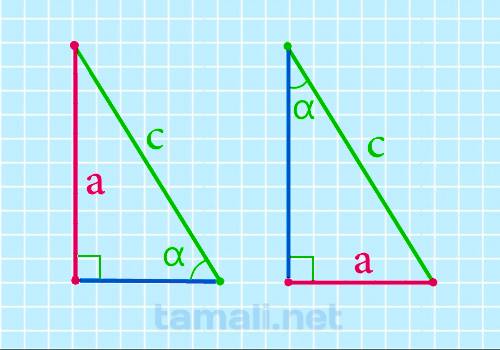
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:

a = c * sin α

где c — гипотенуза, α — острый угол прямоугольного треугольника.

Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее:  a = 77 * 0,98 = 75,8см.

Катет прямоугольного треугольника через гипотенузу и другой известный катет

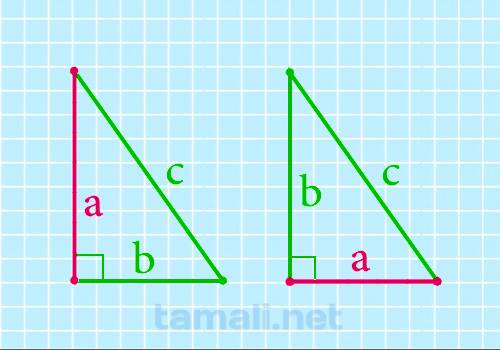
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:

a = √(c² — b²)

где c — гипотенуза, b — катет который известен прямоугольного треугольника.

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см

Гипотенуза прямоугольного треугольника через катет и острый угол

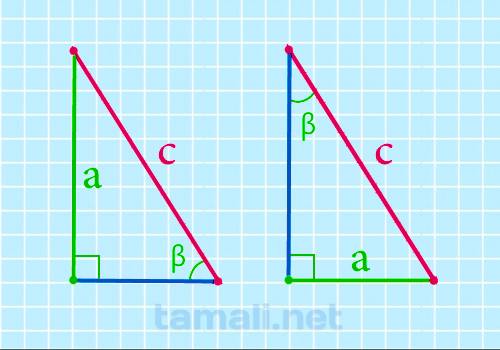
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:

c = a / sin(β)

где a — катет, β — острый угол прямоугольного треугольника.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.

Гипотенуза прямоугольного треугольника через катеты

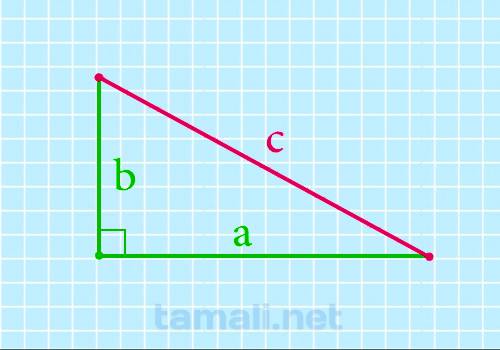
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:

c = √(a² + b²)

где c — гипотенуза, a и b — катеты.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см

Сторона треугольника через две известные стороны и угол между ними

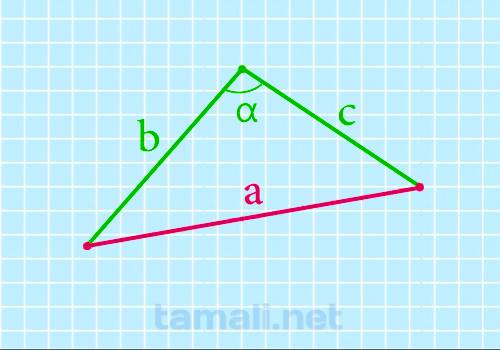
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:

a = b² + c² — 2bc * cos α

где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.

Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.

Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.

Сторона треугольника через известную сторону и два угла

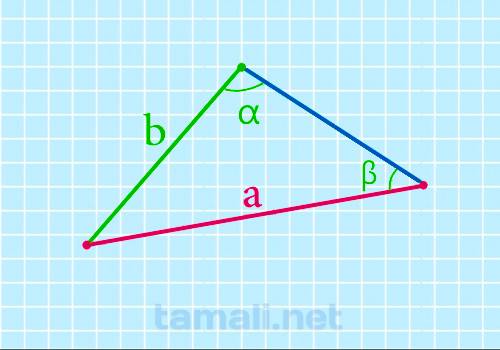
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:

a = (b * sin α) / sin β

где b — сторона треугольника; β, α — углы треугольника.

Пример. Пусть сторона треугольника b равна 10, угол β  = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30   = 8.71723 мм.