Вычисление правильного восьмиугольника (многоугольник с восемью вершинами). Эта форма хорошо нам знакома, так как используется на некоторых дорожных знаках.
.
Поделиться расчетом:
Калькулятор восьмиугольника, введите одно известное значение
Длина стороны(a)
Меньшая диагональ(d1)
Средняя диагональ(e)
Большая диагональ(d3)
Периметр(p)
Площадь(S)
Радиус описанной окружности(R)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:
 d = a * √4 + 2 * √2
d = a * √4 + 2 * √2
e = a * ( 1 + √2 )
f = a * √2 + √2
Высота = e = 2 * r
Р = 8 * а
S = 2 * a2 * ( 1 + √2 )
R = a / 2 * √4 + 2 * √2
r = a / 2 * ( 1 + √2 )
Угол: 135°, 20 диагоналей.
Octagon
share
feedback
calculator
info
history
</>
Octagon (Area, Perimeter & Side) Calculator
getcalc.com’s octagon calculator is an online basic geometry tool to calculate area, perimeter & side of a octagonal shaped polygon, in both US customary & metric (SI) units.
Steps to Find Area of a Octagon
The step by step workout for how to find what is the area of a octagon. Students may use this octagon calculator to generate work with steps for any other similar input values.Workout :
step1 Address the formula, input parameters and values
side = 10 in
step 2 Find Area of Octagon using side value
Area A = 2 (1 + √2 ) s²
= 2 x (1 + √2 ) x (10)² in²
= 2 x (1 + 1.4142 ) x 100 in²
= 2 x 2.4142 x 100 in²
Area A = 482.8427 in²
Octagon & Formulas
Octagon is a polygon with eight straight sides and angles, a geometric shape on the two dimensional plane. K-12 students may refer the below formulas to know what are all the input parameters are being used to find the area, perimeter & side of octagon.

Problems on Finding the Area & Perimeter of Octagon

Татьяна Кеш
Знаток
(342),
закрыт
14 лет назад
Найдите сторону правильного восьмиугольника, вписанного в ту же окружность. (Геометрия 9класс Атанасян)
Matricfria
Мыслитель
(5124)
14 лет назад
1) Если периметр правильного треугольника равен 45см, то сторона равна 15см.
2) Нати радиус окружности. R = a/V3 = 15/V3 = 5*V3см
3) Для правильного восьмиугольника: 360:8 = 45 градусов – центральный угол
4) По теореме косинусов найти сторону правильного восьмиугольника.
a^2 = 75 + 75 – 2*75*cos45
a^2 = 150 – 75*V2 = 75(2 – V2)
a = sqrt(75*(2 – V2)) = 5*sqrt(6 – 3V2)
Как найти сторону правильного многоугольника
Фигура, образованная более чем из двух линий, замыкающихся между собой, называется многоугольником. Каждый многоугольник имеет вершины и стороны. Любой из них может быть правильным или неправильным.
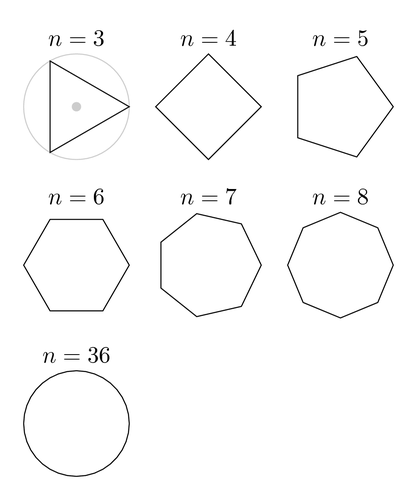
Инструкция
Правильным многоугольником называется фигура, у которой все стороны равны. Так, например, равносторонний треугольник представляет собой правильный многоугольник, состоящий из трех замкнутых линий. В данном случае, все его углы равны 60 °. Его стороны между собой равны, но не параллельны друг другу. Таким же свойством обладают и другие многоугольники, однако, углы у них имеют другие величины. Единственный из правильных многоугольников, у которого стороны не только равны, но и попарно параллельны – квадрат.Если в задаче дан равносторонний треугольник с площадью S, то его неизвестную сторону можно найти через углы и стороны. Прежде всего, найдите высоту треугольника h, перпендикулярную к его основанию:h=a*sinα=a√3/2, где α=60° – один из углов, прилежащих к основанию треугольника.Руководствуясь этими соображениями, преобразуйте формулу для нахождения площади таким образом, чтобы по ней можно было вычислить длину стороны:S=1/2a*a√3/2=a^2*√3/4Отсюда следует, что сторона a равна:a=2√S/√√3
Сторону правильного четырехугольника найдите, пользуясь несколько иным способом. Если он представляет собой квадрат, в качестве первоначальных данных используйте его площадь или диагональ:S=a^2Следовательно, сторона a равна:a=√SКроме того, если дана диагональ, то сторону можно вычислить и по другой формуле:a=d/√2
В большинстве случаев сторону правильного многоугольника можно определить, зная радиус вписанной в него или описанной вокруг него окружности. Известно, что имеется взаимосвязь между стороной треугольника и радиусом окружности, описанной вокруг этой фигуры:a3=R√3, где R – радиус описанной окружностиЕсли окружность вписана в треугольник, то формула приобретает другой вид:a3=2r√3, где r – радиус вписанной окружностиУ правильного шестиугольника формула для нахождения стороны при известном радиусе описанной (R) или вписанной (r) окружностей выглядит следующим образом:a6=R=2r√3/3Из этих примеров можно сделать вывод, что для всякого произвольного n-угольника формула для нахождения стороны в общем виде выглядит следующим образом:a=2Rsin(α/2)=2rtg(α/2)
Источники:
- сторона правильного многоугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Формулы:
d = a * √ 4 + 2 * √2
e = a * ( 1 + √ 2 )
f = a * √ 2 + √2
p = 8 * a
S = 2 * a² * ( 1 + √2 )
re = a / 2 * √ 4 + 2 * √2
ri = a / 2 * ( 1 + √2 )
Длина, высота, периметр и радиус имеют одинаковые метрические единицы (например, метры), площадь – те же единицы, возведенные в квадрат (например, квадратный метр).
![]()
