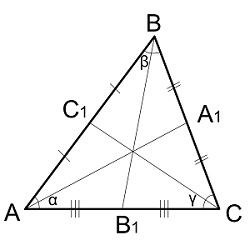
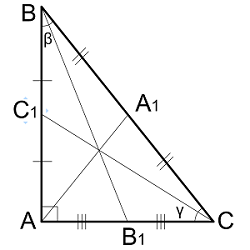
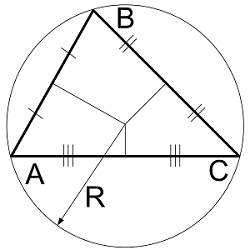
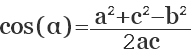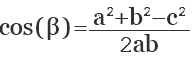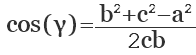Как узнать стороны треугольника, если известны углы?
Знаток
(266),
закрыт
9 лет назад
为什么翻译?
Просветленный
(21263)
9 лет назад
это прямоугольный треугольник. KN катет KM катет MN гипотенуза. вот основные моменты (аштитипи). www-formula.ru/index.php?option=com_content&view=category&layout=blog&id=46&Itemid=167
目的是什么利益?
Оракул
(58091)
9 лет назад
“Напротив большого угла лежит большая сторона! Значит, против угла К=90 лежит гипотенуза МN” хоть понял, что сказал? в прямоугольном треугольнике гипотенуза лежит ВСЕГДА напротив угла в 90 градусов.
Мария Колесникова
Мыслитель
(8416)
9 лет назад
Я обожаю прямоугольные треугольники, у которых один из углов равен 30! 🙂 Знаете, есть одно замечательное правило: катет, лежащий против угла в 30 градусов равен половине гипотенузы. Тогда, можно догадаться, что гипотенуза MN=2*KN. Находить стороны можно по нескольким теоремам (главное, чтобы соответствующие элементы были известны) : по теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) , по теореме синусов (стороны треугольника пропорциональны синусам противолежащих углов) , по теореме косинусов (квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними) , по любой теореме о площади треугольника.
Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет
где a и b – катеты, с – гипотенуза.
2) Найти гипотенузу по двум катетам
где a и b – катеты, с – гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу
где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол
где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними
где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании
где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.
3) Найти боковые стороны по углу между ними
где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании
где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь
где a – искомая сторона, S – площадь треугольника.
2) Найти сторону через высоту
где a – искомая сторона,h – высота треугольника.
3) Найти сторону через радиус вписанной окружности
где a – искомая сторона,r – радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности
где a – искомая сторона,R – радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)
где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)
где a – искомая сторона, b – известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c – стороны произвольного треугольника
α, β, γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.
H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b – катеты прямоугольного треугольника
с – гипотенуза
α – угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L – биссектриса, отрезок ME , исходящий из острого угла
a, b – катеты прямоугольного треугольника
с – гипотенуза
α, β – углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L – высота = биссектриса = медиана
a – одинаковые стороны треугольника
b – основание
α – равные углы при основании
β – угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L – высота=биссектриса=медиана
a – сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана
R – радиус описанной окружности
O – центр описанной окружности
с – гипотенуза
a, b – катеты
α – острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Как найти стороны треугольника, если даны все углы
Для того, чтобы узнать все стороны треугольника, нужно знать величину угла и два прилегающих к нему катета или величину двух углов и стороны между ними. Если вам известны все углы этого треугольника, то найти длину всех сторон треугольника нельзя, но можно найти отношение сторон этого треугольника.

Инструкция
В первом случае известны такие данные в треугольнике, как величина угла и длина катетов, образующих этот угол. Сторону, противолежащую известному углу, необходимо находить по теореме косинусов, согласно которой необходимо длины известных сторон возвести в квадрат и сложить, затем отнять от полученной суммы произведение этих сторон, умноженное на два и на косинус известного угла.
Формула данного вычисления выглядит следующим образом:
h = √(e2+f2 – 2ef*cosA), где:
e и f – длины известных катетов;
h – неизвестный катет (или сторона);
A – угол, образованный известными катетами.
Во втором случае, когда известны два угла и катет между ними данного треугольника, нужно пользоваться теоремой синусов. Согласно данной теореме, если разделить синус угла на его длину противолежащего катета, то получится отношение, равное любому другому в этом треугольнике. Также, если вам неизвестен нужный катет, вы можете его легко найти, зная тот факт, что сумма углов треугольника равна стам восьмидесяти градусам.
Данное утверждение можно представить в виде формулы:
SinD/d = sinF/f = sinE/e, где:
D, F, E – величины противолежащих углов;
d, f, e – катеты, противолежащие соответствующим углам.
В третьем случае известны только углы данного треугольника, поэтому нельзя узнать длину всех сторон данного треугольника. Зато можно найти отношение этих сторон и методом подбора найти похожий треугольник. Отношение сторон данного треугольника находится с помощью составления системы из трех уравнений с тремя неизвестными.
Вот формула для составления:
d/sinD
f/sinF
e/sinE, где:
d, f, e – неизвестные катеты треугольника;
D, F, E – углы, противолежащие неизвестным катетам.
Данное уравнение решается следующим образом:
d/sinD = f/sinF = e/sinE
(d*sinF*sinE-f* sinD* sinE-e* sinD* sinF)/ sinD* sinE* sinF.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти сторону треугольника?
Как найти длину одной из сторон треугольника? Какие есть формулы?
Формул для нахождения стороны треугольника не так уж много, но главное не знать их — а успешно применять при решении задач, ведь далеко не каждую задачу можно решить в лоб.
Сейчас на примере я покажу, как нужно их применять.
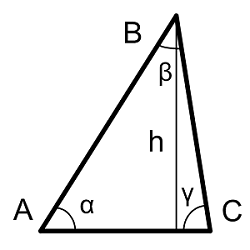
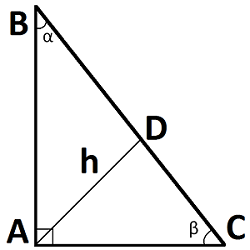
Есть произвольный треугольник со стороной 18 см, один угол при нем равен 30 градусам, а площадь равна 36 см.кв. Нужно найти две другие стороны. Сделаем рисунок
Для решения задачи проведем к основанию (с=18см) высоту h и тем самым разделим наш треугольник на два прямоугольных.
Исходя из формулы площади, найдем высоту
S = 1/2h*c откуда h = 2S/c = 2*36/18 = 4 см
Теперь находим сторону b по синусу угла
sin = h/b (отношение противоположного катета к гипотенузе) откуда b = h/(sin 30) = 4/(1/2) = 8 см.
Мы уже знаем две стороны у угол между ними и третью сторону можно найти по формуле из теоремы косинусов, но к сожалению не всегда мы ее помним. В нашем случае ничего страшного — найдем сторону а по формуле Пифагора, но для начала нам нужно найти сторону х.
Можно по формуле Пифагора
откуда х = квадратный корень из (8*8 — 4*4), что равно 4*(кв.к3)
и находим последнюю сторону нашего треугольника
а = кв.к из (c-x)*(c-x) + h*h = кв.к из 18*18-2*18*4*(кв.к3)+4*(кв.к3)*4*(кв.к3)+4*4
здесь стоит обратить внимание, что
4*(кв.к3)*4*(кв.к3)+4*4 = 4*4*3+4*4 = 4*4*4 = 4*2*2*2 = 8*8 = b*b
2*18*4*(кв.к3) = 2*18*4*2*(кв.к3/2) = 2*18*8*(кв.к3/2) = 2*с*b*cos30 и теперь можно записать
а = кв.к из с*с — 2*с*b*cos30 + b*b Что на самом деле есть формулой нахождения стороны треугольника по теореме косинусов (мы ее только что вывели)
Теперь посчитаем и найдем сторону а = 11,772 см.
Существует целый ряд формул, с помощью которых можно найти сторону треугольника.
Рассмотрим 2 варианта:
1) Сторона треугольника через 2 других стороны и угол между ними.
Пусть a и b — известные стороны, α — угол между ними. Формула будет такой:
c = √(a² + b² — 2ab * cosα).
В треугольнике ABC сторона AB = 6 см, сторона AC = 10 см, угол меду ними = 60º.
Сторона BC = √(36 + 100 — 120 * 0,5) = √(136 — 60) = √76 = 2√19 = 8,72 см.
2) Сторона треугольника через два угла и сторону.
Здесь можно воспользоваться теоремой синусов.
Если даны углы α и β, а также сторона c, то две другие стороны можно найти по формулам:
a = c * (sinα / sinγ), где γ = 180° — α — β.
b = c * (sinβ / sinγ).
c = 10 см, α = 30°, β = 45°.
a = 10 * (0,5 / 0,96) = 5,21 см.
b = 10 * (0,7 / 0,96) = 7,29 см.
Кроме того, треугольник может быть равнобедренным или прямоугольным — в этом случае специфика нахождения длины стороны будет немного другой.
Например, для нахождения катетов или гипотенузы можно воспользоваться теоремой Пифагора.
Есть еще формулы для равнобедренного треугольника (это треугольник у которого две стороны равны и углы при оснавании также равны между собой). Для такого треугольника основание можно рассчитать по формулам:
b = 2a*sin(x/2) = a*√(2-2cosx)
Где b — длина оснавания, а — длина равных сторон, х — равные уголы при оснавании, у — угол образованный равными сторонами (лежит напротив основания).
Для того чтобы найти равные стороны равнобедренного треугольника можно использовать вот эти формулы:
a = b/(2*sin(x/2)) = b/√(2-2cosx)
Для рассчетов по этим формулам нужно знать длину хотябы одной стороны и хотябы один угол. Так как зная величину одного любого угла в равнобедренном треугольнике можно найти все остальные углы исходя из теоремы о сумме углов треугольника (сумма всех углов любого треугольника равна 180°)
Углы треугольника
Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.
α = 180°-β-γ
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
a 2 = b 2 + c 2 + 2abc cos (α)
Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:
cos (α) = (b 2 + c 2 — a 2 ) / 2bc
,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.
Формулы треугольника
Для расчёта всех основных параметров треугольника воспользуйтесь калькулятором.
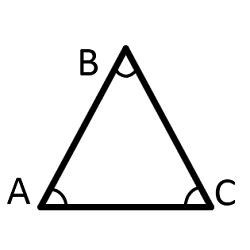
Виды треугольников
-
Остроугольный треугольник — это треугольник, в котором все три угла острые, т.е. меньше 90°. -
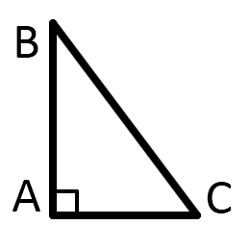
Прямоугольный треугольник — это треугольник, содержащий прямой угол.
Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС).
Свойства треугольника, применимые к любому треугольнику:
- Против большей стороны лежит больший угол, и наоборот.
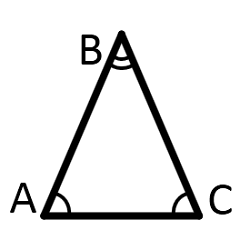
- Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.)
- Сумма углов треугольника равна 180° (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60°).
- Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ.
- Любая сторона треугольника меньше суммы двух других сторон и больше их разности:
- $$ AB BC — CA $$
- $$ BC AB — CA $$
- $$ CA AB — BC $$
Признаки равенства треугольников
Произвольные треугольники равны, если:
Три стороны одного треугольника равны трем сторонам другого треугольника (по трем сторонам).
Две стороны одного треугольника равны двум сторонам другого треугольника и углы между этими сторонами также равны (по двум сторонам и углу между ними).
AB = DE и BC = EF и ∠ABC = ∠DEF;
BC = EF и AC = DF и ∠BCA = ∠EFD;
AB = DE и AC = DF и ∠CAB = ∠FDE;
Три угла одного треугольника равны трем углам другого треугольника (по трем углам).
Два угла одного треугольника равны двум углам другого треугольника, и любая сторона первого треугольника равна соответствующей стороне другого треугольника.
AB = DE или BC = EF или AC = DF
Прямоугольные треугольники равны, если равны:
- Гипотенуза и острый угол.
BC = EF и ∠ABC = ∠DEF
BC = EF и ∠BCA = ∠EFD;
AB = DE и ∠BCA = ∠EFD
AC = DF и ∠ABC = ∠DEF
AB = DE и ∠ABC = ∠DEF
AC = DF и ∠BCA = ∠EFD
AB = DE и AC = DF
AB = DE и BC = EF
AC = DF и BC = EF
Подобные треугольники
Два треугольника являются подобными, если углы одного треугольника равны, углам тругого треугольника, а стороны подобны
- ∠ABC = ∠DEF и ∠BCA = ∠EFD и ∠CAB = ∠FDE;
- $$ = = = К_ $$
Признаки подобия треугольников
- Два угла одного треугольника равны двум углам другого треугольника.
- Две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны.
- Три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.
Свойства подобных треугольников.
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия (Kподобия) $$ over S_> = К_^2 $$
- Отношение периметров и длин биссектрис, медиан, высот, серединных перпендикуляров равно коэффициенту подобия. т.е. в подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.
Подобие в прямоугольных треугольниках.
- Треугольники, образованные высотой, опущенной из прямого угла, являются подобными друг другу
- Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
- Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
- Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
Площадь треугольника
Где: AB,BC,AC – стороны треугольника h – высота треугольника α, β, γ– углы треугольника P – полупериметр AC – основание треугольника Площадь произвольного треугольника
Площадь треугольника по формуле Герона
Площадь треугольника по углу и двум сторонам
Площадь треугольника по двум углам и стороне
Площадь прямоугольного треугольника по катетам
Где: AB,AC – катеты треугольника $$ S = * AB * AC $$
Площадь равнобедренного треугольника
Где: AB,BC – равные стороны треугольника AC – основание треугольника $$ S = * sqrt $$
Площадь равностороннего треугольника
Где: AB,BC,AC – равные стороны треугольника h – высота треугольника $$ S = over 4> * AB^2 $$ $$ S = > $$
Стороны треугольника
Где: AB,BC,AC – стороны треугольника h – высота треугольника α, β, γ– углы треугольника P – полупериметр AC – основание треугольника Сторона треугольника по двум сторонам и углу
Сторона треугольника по стороне и двум углам
Сторона прямоугольного треугольника
Где: AB,AC – катеты треугольника BC – гипотенуза треугольника $$ AC = BC * cos(β) = BC * sin(α) = AB * tg(α) $$ $$ AB = BC * cos(α) = BC * sin(β) = AC * tg(β) $$ $$ BC = = $$ $$ BC = = $$
Сторона прямоугольного треугольника по теореме Пифагора.
Сторона равнобедренного треугольника
Где: AB,BC – равные стороны треугольника AC – основание треугольника $$ AC = 2 * AB * sin() = AB * sqrt $$ $$ AC = 2 * AB * cos(α) $$ $$ AB = = > $$ $$ AB = $$
Высота треугольника
Высота – это перпендикуляр, выходящий из любой вершины треугольника, к противоположной стороне или её продолжению для треугольника с тупым углом. Высоты треугольника пересекаются в одной точке
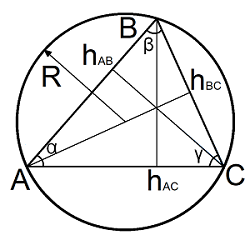
Где: AB,BC,AC – стороны треугольника h – высота треугольника P – полупериметр $$ P = $$ α, β, γ – углы треугольника R — радиус описанной окружности S — площадь треугольника Высота на сторону АС, hAC
Высота на сторону AB, hAB
Высота на сторону BC, hBC
Формула длины высоты через сторону и угол
Высота на сторону АС, hAC
Высота на сторону AB, hAB
Высота на сторону BC, hBC
Формула длины высоты через сторону и площадь
Высота на сторону АС, hAC
Высота на сторону AB, hAB
Высота на сторону BC, hBC
Формула длины высоты через стороны и радиус
Высота на сторону АС, hAC
Высота на сторону AB, hAB
Высота на сторону BC, hBC
Формулы высоты из прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
Где: AB,AC – катеты треугольника BC – гипотенуза треугольника BD, DC – отрезки полученные от деления гипотенузы, высотой α, β– углы треугольника Формула длины высоты через гипотенузу и острые углы
Формула длины высоты через катет и угол
Формула длины высоты через составные отрезки гипотенузы
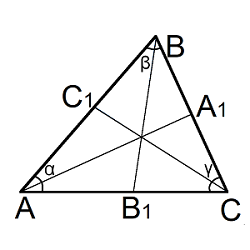
Биссектрисы в треугольнике
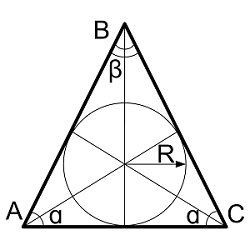
Биссектриса – это отрезок, который делит угол пополам из которого выходит. Точка пересечения всех трех биссектрис треугольника совпадает с центром вписанной окружности.
Где: AB,BC,AC – стороны треугольника AA1,BB1,CC1 — биссектрисы в треугольнике α, β, γ– углы треугольника P – полупериметр $$ P = $$ Длина биссектрисы через две стороны и угол
Длина биссектрисы через полупериметр и стороны
Длина биссектрисы через три стороны
Длина биссектрисы через стороны и отрезки, на которые делит биссектриса
Формула длины биссектрис в прямоугольном треугольнике
Где: AB,AC – катеты треугольника BC – гипотенуза треугольника β, γ– острые углы треугольника Длина биссектрисы из прямого угла, через катеты.
Длина биссектрисы из прямого угла, через гипотенузу и угол
Длина биссектрисы через катет и угол
Длина биссектрисы через катет и гипотенузу
Длина биссектрисы равнобедренного треугольника
Где: AB,BC – равные стороны треугольника AC – основание треугольника α – равные углы при основании треугольника β – угол образованный равными сторонами треугольника Длина биссектрисы через стороны и угол, равнобедренного треугольника
Длина биссектрисы через стороны, равнобедренного треугольника
Длина биссектрисы равностороннего треугольника
Где: AB,BC,AC – равные стороны треугольника $$ BB_1 = over 2> $$
Медиана в треугольнике
Медиана – это отрезок, который выходит из вершины и делит противоположную сторону пополам. Медиана делит треугольник на два равных по площади треугольника.
Где: AB,BC,AC – стороны треугольника AA1,BB1,CC1 — медианы в треугольнике α, β, γ– углы треугольника Длина медианы через три стороны
Длина медианы через две стороны и угол между ними
Длина медианы в прямоугольном треугольнике, выходящая из прямого угла.
Где: AB,AC – катеты треугольника BC – гипотенуза треугольника AA1,BB1,CC1 — медианы в треугольнике β, γ– острые углы треугольника Длина медианы в прямоугольном треугольнике, выходящая из прямого угла, равна радиусу описанной окружности, а середина гипотенузы является центром описанной окружности
Длина медианы через катеты
Длина медианы через катет и острый угол
Описанная окружность
Радиус описанной окружности произвольного треугольника по сторонам
Где: AB,BC,AC – стороны треугольника P – полупериметр $$ P = $$ R — радиус описанной окружности $$ R = > $$
Радиус описанной окружности равностороннего треугольника по стороне или высоте