3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).

Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.

Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 – 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
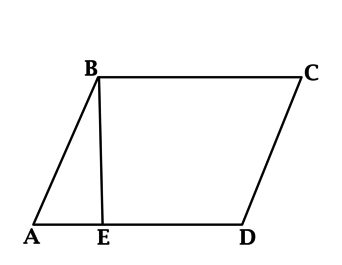
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
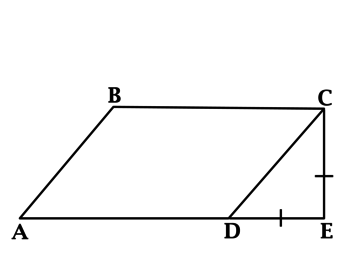
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} – 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).

По теореме Пифагора находим: (AB^2=AD^2 – BD^2 = 25 – 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ

В параллелограмме (ABCD): (P_{triangle AOB} = 8), (P_{triangle AOD} = 9), а сумма смежных сторон равна (7). Найдите произведение этих сторон параллелограмма (ABCD).
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} – P_{triangle AOB} = AD – AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.

Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни
![]()
2
Как найти сторону параллелограмма?
Как найти длину одной из сторон параллелограмма?
3 ответа:
![]()
3
0
Чтобы найти сторону параллелограмма, необходимо наличие некоторых других значений, которые бы были известны. Далее попросту использовать одну из подходящих формул.
Например, по теореме косинусов, это формулы сторон через диагонали и находящийся между ними угол:
Другим решением, являются формулы, где стороны рассчитываются по диагонали и одной из известной стороны:
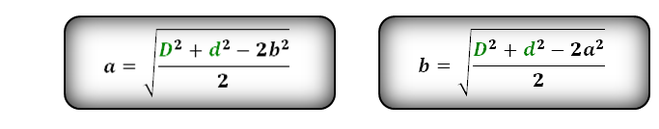
Вот еще формулы сторон параллелепипеда, через вторую сторону, диагонали и косинус угла:

Стоит напомнить и про формулы длин сторон, через высоту и синус угла:
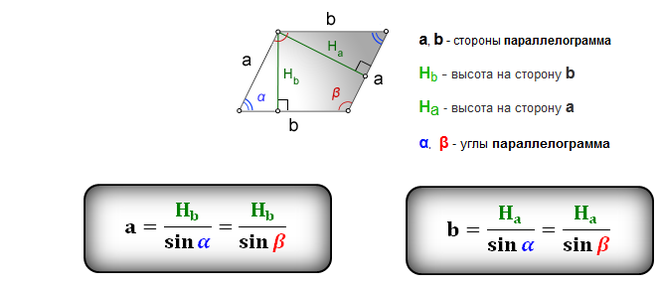
Так же длину стороны параллелограмма, можно определить если известны площадь и высота:
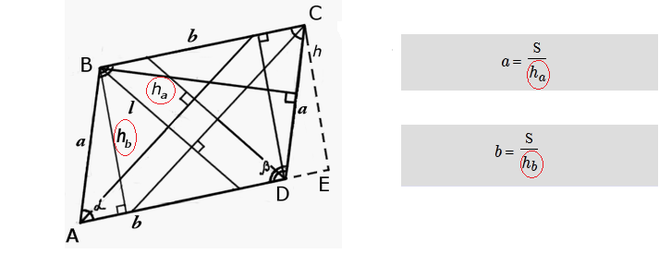
Как видим, вариантов расчета высоты параллелограмма достаточно много и хотелось напомнить основные характеристики этой геометрической фигуры:
Во первых, параллелограммом называется четырехугольник, имеющий параллельно расположенные противоположные стороны , т. е. находящиеся на параллельных прямых. Квадраты, прямоугольники и ромбы, также являются параллелограммами.
![]()
2
0
Для нахождения стороны параллелограмма есть более десятка разных формул (они перечислены в ответе автора Бульбозавр), но для решения задач на эту тему, далеко не всегда их можно применить.
На мой взгляд лучше всего разобрать несколько примеров и на практике увидеть, как находить сторону этой фигуры – в наших случаях с помощью уравнений.
Пример 1
Нужно найти стороны параллелограмма, если одна из сторон больше другой в два раза а периметр равен 30 см.
Даже не нужно чертить рисунок, а просто составить уравнение и решить его
периметр(30см) = 2(х+2х) откуда х=5см, следовательно одна сторона равна 5см, другая – 10см.
Пример 2
АВСД – параллелограмм, нужно найти его стороны если – ВМ перпендикуляр к АС, АМ=6см, МС=15см, ВС больше АВ на 6 см

Для решения этой задачи сначала рассматриваем два прямоугольных треугольника АВМ и ВСМ у которых общий катет h.
Согласно Пифагору
h*h=a*a-6*6=b*b-15*15 откуда b*b-a*a=(b-a)(b+a)=225-36=189
по условию задачи b-a=7 тогда b+a=189/7=27
решив эту простенькую систему уравнений найдем стороны a=10см b=17cм
![]()
1
0
Есть еще несколько формул которые будут скорее вспомогательными при решении задач по нахождению стороны паралелограмма но тем не менее их тоже нужно знать. Например одну из сторон паралеллограмма можно найти если известна вторая сторона и периметр фигуры по формуле:
Р = 2(а+b), тогда а = (Р/2 – b), или b = (P/2 – a), где Р – периметр, а и b – стороны.
Также можно найти сторону паралеллограмма зная его площадь и высоту опущенную на искомую сторону:
S = a*H1 = b*H2, тогда а = S/H1 или b = S/H2, где S – площадь, а – меньшая сторона паралелограмма, b – большая сторона, Н1 – высота построенная к меньшей стороне, Н2 – сторна построенная к большей стороне паралеллограмма.
Читайте также
![]()
Насколько я помню из школьных уроков геометрии, параллелепипед имеет шесть граней и их количество не зависит от размеров углов основания и граней. В качестве примера привожу скриншоты самого параллели пела и его, так сказать, “развёрнутого” вида.
![]()
Однозначно удлиненный. Проверочное слово – длина.
![]()
Прямым углом в геометрии называется угол, образованный двумя перпендикулярными прямыми и он равен 90 градусам. Два одинаковых прямоугольных треугольника, совмещённых, как показано на рисунке ниже, образуют прямоугольник, сумма углов которого равняется, как мы знаем, 360 градусам (4 угла по 90 градусов).

Поскольку треугольники у нас одинаковы, то разделив 360 градусов на 2, мы получим, что сумма углов каждого из треугольников равняется 180 градусам. Отняв от 180 градусов наш прямой угол (90 градусов), мы получим сумму двух острых углов, а именно – тоже 90 градусов.
Таким образом, сумма острых углов прямоугольного треугольника равна 90 градусов, а сумма всех его углов равна 180 градусам, как, к слову, и сумма всех углов любого другого треугольника.
![]()
Теорема Пифагора устанавливает соотношение между тремя сторонами прямоугольного треугольника. Об этом соотношении знали до Пифагора. Так, еще в древнекитайской книге Чу-пей пишется о таком треугольнике со сторонами 3, 4 и 5. И даже предложен рисунок, который совпадает с чертежом индусской геометрии Басхары. Точной даты неизвестно, но где-то 1000 лет до нашей эры.
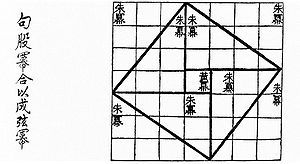
Слева надпись на китайском языке: сумма квадратов длин высоты и основания равна квадрату длины гипотенузы.
Однако равенство
3^2 + 4^2 = 5^2
было известно еще египтянам за 23 века до н.э. Они строили прямые углы с помощью веревок длиной 3, 4 и 5 (каких единиц длины, не помню). Но это не важно. Хотя доказательства не знали. На сегодня имеется почти 400 способов доказательства теоремы Пифагора. Пифагор дата жизни 570-490 годы до н.э. Сам Пифагор доказал эту теорему, построив прямоугольники на трех сторонах прямоугольного треугольника.
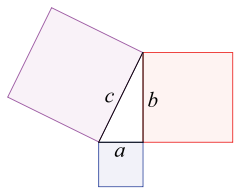
Сумма площадей квадратов, построенных на катетах, равна площади квадрата, опирающегося на гипотенузу. Я помню такую формулировку: Пифагоровы штаны во все стороны равны. Доказательство довольно сложное (особенно трудно писать математические уравнения на БВ). Не буду приводить. Но самое простое доказательство – чисто алгебраическое. Но и оно требует написания нескольких сложных уравнений. Вот наиболее общее уравнение теоремы Пифагора
a^2 + b^2 = c^2.
То есть сумма квадратов катетов равна квадрату гипотенузы. Здесь a и b – длины катетов, c – длина гипотенузы. Так что точных геометрических построений проводить не надо. Можно, конечно, построить три квадрата, взять линейку и измерить длины сторон этих a, b и с. Но это будет не абсолютно точное доказательство. Погрешность измерения линейкой мешает. Именно так древние египтяне и «доказали» вышеприведенное равенство.
![]()
Посмотри на вот этом сайте! http://mymath213.blo<wbr />gspot.ru/p/10.html
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
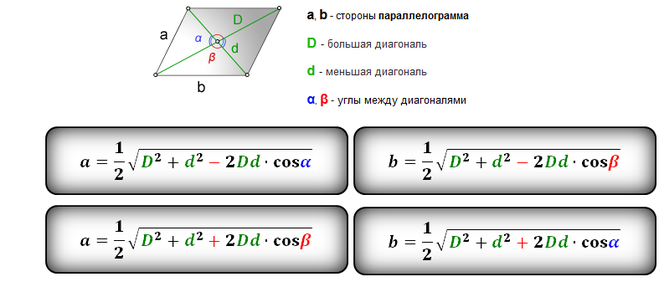
1. Формулы длины сторон через диагонали и угол между ними.
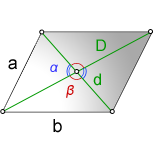
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
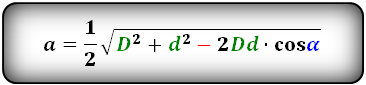

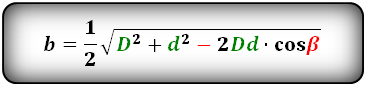
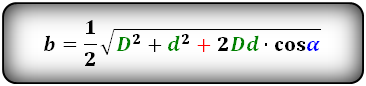
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
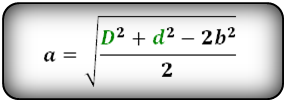
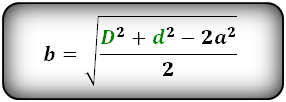
Формулы сторон параллелограмма , (a, b):

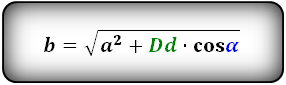
2. Формулы длины сторон параллелограмма через высоту.
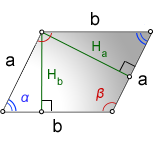
a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
α, β – углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
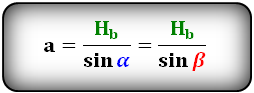
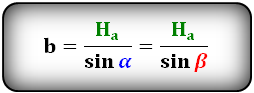
3. Дополнительные, интересные формулы параллелограмма:
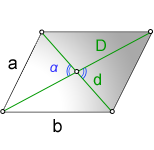
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
Формула суммы квадратов диагоналей:
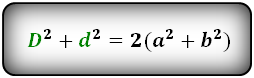
Формула разности квадратов сторон:
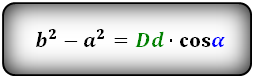
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 31 октября 2011
-
Обновлено: 13 августа 2021
Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.
 Определение
Определение
Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.
 На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь
На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь 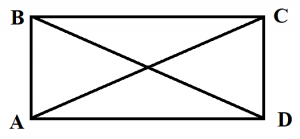
- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
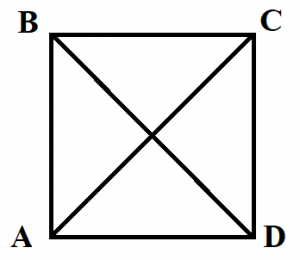
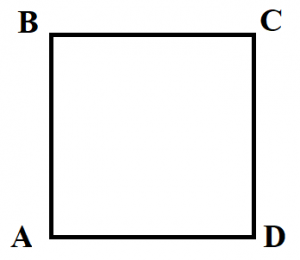 Свойства квадрата
Свойства квадрата
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Параллелограмм: свойства и признаки

О чем эта статья:
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a × h, где a — сторона, h — высота.
- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
- Противоположные стороны параллелограмма равны.
ABCD — параллелограмм, значит, AB = DC, BC = AD. - Противоположные углы параллелограмма равны.
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D. - Диагонали параллелограмма точкой пересечения делятся пополам.
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC. - Диагональ делит параллелограмм на два равных треугольника.
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA. - Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°. - В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.
Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Параллелограмм. Формулы, признаки и свойства параллелограмма
Признаки параллелограмма
AB||CD, AB = CD (или BC||AD, BC = AD)
∠DAB = ∠BCD, ∠ABC = ∠CDA
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Основные свойства параллелограмма
∠ABC = ∠CDA, ∠BCD = ∠DAB
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d 1 |
| 2 | |
| BO = DO = | d 2 |
| 2 |
AC 2 + BD 2 = 2AB 2 + 2BC 2
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
2. Формула сторон параллелограмма через диагонали и другую сторону:
| a = | √ 2 d 1 2 + 2 d 2 2 – 4 b 2 |
| 2 |
| b = | √ 2 d 1 2 + 2 d 2 2 – 4 a 2 |
| 2 |
3. Формула сторон параллелограмма через высоту и синус угла:
4. Формула сторон параллелограмма через площадь и высоту:
Диагонали параллелограмма
Формулы определения длины диагонали параллелограмма:
d 1 = √ a 2 + b 2 – 2 ab·cosβ
d 2 = √ a 2 + b 2 + 2 ab·cosβ
d 1 = √ a 2 + b 2 + 2 ab·cosα
d 2 = √ a 2 + b 2 – 2 ab·cosα
d 1 = √ 2 a 2 + 2 b 2 – d 2 2
d 2 = √ 2 a 2 + 2 b 2 – d 1 2
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d 1 = | 2S | = | 2S |
| d 2· sinγ | d 2· sinδ |
| d 2 = | 2S | = | 2S |
| d 1· sinγ | d 1· sinδ |
Периметр параллелограмма
Формулы определения длины периметра параллелограмма:
P = 2 a + 2 b = 2( a + b )
P = 2 a + √ 2 d 1 2 + 2 d 2 2 – 4 a 2
P = 2 b + √ 2 d 1 2 + 2 d 2 2 – 4 b 2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
Площадь параллелограмма
Формулы определения площади параллелограмма:
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/svoystva-i-priznaki-parallelogramma
http://ru.onlinemschool.com/math/formula/parallelogram/
[/spoiler]
Ты параллелограммы многоугольники плоская геометрия широко изучается как обычные геометрические фигуры в нашей повседневной жизни. Мы определяем параллелограмм как многоугольник, имеющий противоположные стороны параллельны, характеристика, которая приводит к исключительным свойствам.
Частными случаями параллелограммов являются квадраты, прямоугольники и ромбы. Для каждого из этих многоугольников есть свои формулы для расчета площади и периметра.
Читайте тоже: Круг и окружность – геометрические фигуры с множеством особенностей
Элементы параллелограмма
Чтобы быть параллелограммом, многоугольник должны иметь параллельные противоположные стороны. В качестве специфических особенностей мы должны:
-
Каждый параллелограмм состоит из четырех сторон, а противоположные стороны равны параллели.

-
Каждый параллелограмм имеет четыре внутренних угла, а сумма этих углов всегда равен 360º.

-
У каждого параллелограмма две диагонали.

Помните, что параллелограммы частные случаи четырехугольники, поэтому есть особенности, унаследованные от этих геометрических фигур, такие как наличие двух диагоналей, четыре стороны и четыре угла, а также сумма внутреннего и внешнего углов всегда равна 360º.
Свойства параллелограмма
-
1-й объект: Противоположные стороны параллелограмма равны, то есть имеют одинаковую меру.

-
2-е свойство: Противоположные углы параллелограмма равны, а два последовательных угла всегда являются дополнительными (сумма равна 180 °).
Зная, что AB и CD параллельны, тогда стороны BC и AD поперечны AB и CD; следовательно, углы сформированные (w и x) являются дополнительными, поскольку они являются внутренними боковыми углами. Кроме того, можно показать, что углы x и z совпадают.


- 3-е свойство: Диагонали параллелограмма разрезаются пополам.
Когда мы рисуем две диагонали параллелограмма, их точка встречи делит каждую на ее середины.
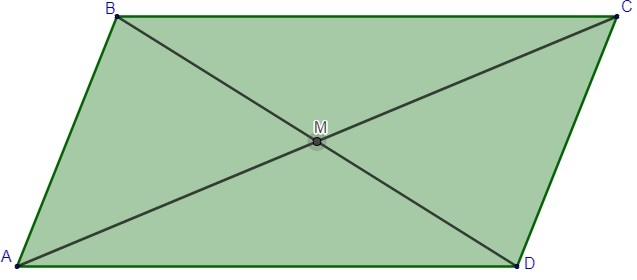
AM = см
BM = DM
Смотрите также: Точка, линия, плоскость и пространство: основные понятия геометрии
Площадь параллелограмма
Площадь параллелограмма, в общем, рассчитывается как произведение основания и высоты. Есть частные случаи (прямоугольники, ромбы и квадраты), которые имеют определенные формулы – они будут представлены в этом тексте – но вытекают из общей формы.

А = b.h
b: база
h: высота
Периметр параллелограмма
О периметр дан кем-то сумма со всех сторон. Поскольку параллелограмм обычно имеет две равные стороны, его периметр можно определить следующим образом:

п = 2 (а + б)
Частные случаи параллелограммов
Как мы знаем, по определению, чтобы быть параллелограммом, многоугольник должен иметь параллельные стороны. Есть три четырехугольника, которые рассматриваются как частные случаи параллелограмма: прямоугольник, ромб и квадрат.
-
Квадратный
мы называем квадратный четырехсторонний многоугольник с четырьмя сторонами и четырьмя равными углами – каждый угол равен точно 90 градусам. Поскольку квадрат является параллелограммом, все свойства действительны для квадрата.

Площадь квадрата и его периметр рассчитываются аналогично тому, как это делается с параллелограммом, но поскольку все стороны квадрата равны, мы можем представить площадь и периметр квадрата следующим образом:
A = l²
P = 4,1
-
Прямоугольник
О прямоугольник это параллелограмм, у которого есть все совпадающие углы. Он получил такое название, потому что все твои углы прямые, то есть четыре угла составляют 90º. Область прямоугольника идентична области параллелограмма, но мы можем рассматривать вертикальную сторону как высоту, в конце концов, она перпендикулярна основанию.

А =а.б
P = 2 (а + б)
-
Алмаз
О алмаз это параллелограмм, у которого все стороны равны. Учтите, что ограничений по углам нет, они могут быть разными или нет. В отличие от предыдущих примеров, Расчет площади алмаза производится по его диагоналям. Также существует очень важная взаимосвязь между диагоналями алмаза и его стороной.

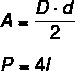
D: большая диагональ
d: малая диагональ
l: сторона
Для любого ромба мы знаем, что диагонали пересекаются в средней точке, образуя четыре прямоугольных треугольника. Анализируя один из этих треугольников, можно увидеть Пифагорейские отношения между стороной и половиной каждой из диагоналей.
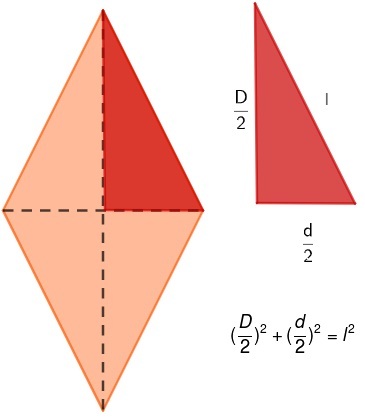
Также доступ: длина окружности и площадь круга
Связь параллелограммов
Важно понимать определение параллелограмма, чтобы не было никаких сложностей при классификации. Всегда полезно помнить, что каждый параллелограмм – четырехугольник, но не каждый четырехугольник – параллелограмм.
Мы также можем утверждать, что каждый прямоугольник, каждый квадрат и каждый ромб являются параллелограммами. Более того, сравнивая частные случаи параллелограммов, мы можем увидеть другую взаимосвязь, потому что квадрат он имеет конгруэнтные углы, что является определением прямоугольника, а также конгруэнтные стороны, что является определением алмаз. Как следствие, можно сказать, что каждый квадрат – это прямоугольник, а также ромб.

решенные упражнения
Вопрос 1 – Зная, что рисунок ниже представляет собой параллелограмм, каковы будут значения x, y и z соответственно?
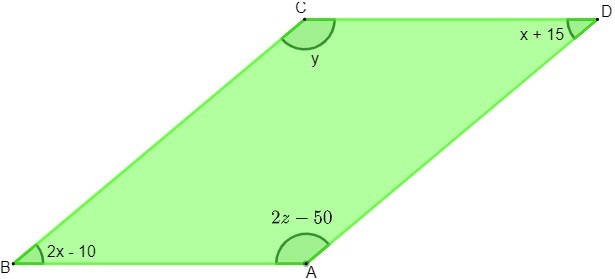
а) 40,140 и 180
б) 30, 100 и 100
в) 25, 140 и 95
г) 30, 90 и 145
д) 45, 55 и 220
разрешение
1 шаг: Используя свойство параллелограмма, мы знаем, что противоположные углы равны. При анализе изображения удобнее использовать это свойство при углах при вершинах B и D, так как они имеют одно и то же неизвестное.
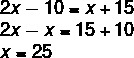
2-й шаг: Зная, что последовательные углы являются дополнительными и что x = 25, можно найти значение y.

3 шаг: Поскольку углы вершин C и A противоположны, они совпадают, поэтому мы можем найти значение z.
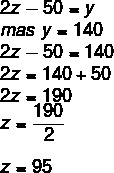
Альтернатива C.
Вопрос 2 – Вычислите площадь параллелограмма (стороны, измеренные в сантиметрах) ниже.
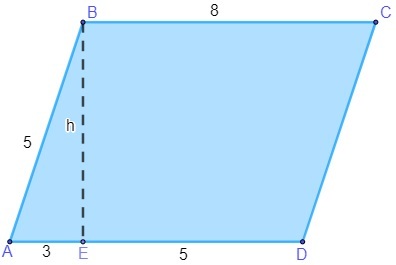
а) 16 см²
б) 32 см²
в) 8 см²
г) 64 см²
д) 40 см²
разрешение
Чтобы найти площадь параллелограмма, сначала необходимо найти значение h. Обратите внимание, что треугольник AEB – это прямоугольник гипотенузы, равный 5, поэтому мы можем применить теорему Пифагора, чтобы найти значение h.
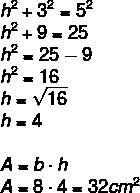
Альтернатива Б.
Рауль Родригес де Оливейра
Учитель математики
Источник: Бразильская школа – https://brasilescola.uol.com.br/matematica/paralelogramos.htm

