Как найти стороны поперечного сечения

Разобъем задачу на 2 части.

В первой части попробуем понять, что за прямоугольник вписанный в окружность с максимальной площадью.

А во второй части найдем его стороны.

1 Часть. Поскольку прямоугольник вписан в окружность, то его диагональ будет являться диаметром окружности (основано на свойстве, что прямой угол опирается на диаметр)

Эта диагональ разбивает прямоугольник на два равных треугольника с одинаковой площадью.

Рассмотрим один из треугольников с основанием равным диаметру. Максимальная площадь у такого треугольника будет при максимальной высоте. А максимальная высота – это радиус окружности проведенный перпендикулярно диаметру. Таким образом получим, что максимальной площади будет равнобедренный треугольник с боковой стороной “х”.

То есть прямоугольник максимальной площади получится квадратом со стороной “х”

2 Часть. Найдем эту сторону “х”. Поскольку это боковая сторона равнобедренного прямоугольного треугольника, то по теореме Пифагора х² + х² = 1²

2•х² = 1

х² = 1/2

х = 1/√2 (берем только положительно, расстояние отрицательным быть не может)

х = √2/2 ≈ 1,41/2 = 0,705

Ответ: х = 0,705

Источник

Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.

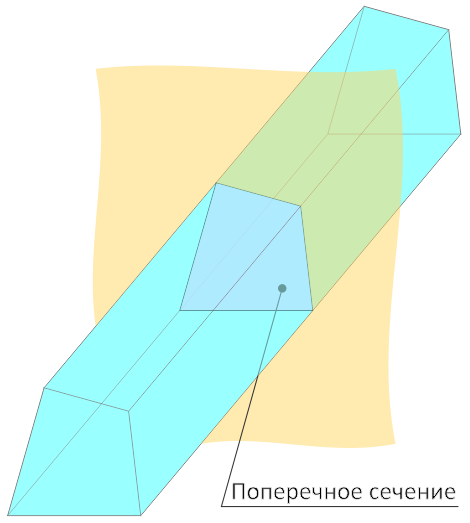
Сечение может иметь простую или сложную форму, а также быть составным.

Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.

Площадь поперечного сечения

В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.

Формулы для расчета площади основных фигур.

Пример:
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.

Для расчета общей площади, сложное сечение раскладывается на простые фигуры:

Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.

В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:

A=A₁+A₂+A₃-A₄

Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м², см² или мм².

Площадь составного сечения

Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.

Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.

Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.

В результате сложив все составляющие профили, получим площадь всего сечения.

Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.

Длина поперечного сечения

Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.

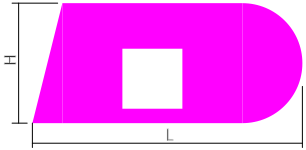
Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.

Ширина сечения определяется аналогично, но обозначается буквой H или h.

При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м².

Понятие «поперечное сечение» является одним из основных при расчетах на прочность в сопротивлении материалов и технической механике.

Различают два основных вида расчета площади сечений:

Геометрический — когда требуется найти площадь сечения тела по известным размерам;
Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.

Пример расчета поперечных сечений >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Площадь поперечного сечения

При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:

S = πR²

При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.

Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:

a² + b² = c²

Из нее можно вывести такую формулу:

c = S*q*r*t*(a² + b²)

Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:

S= c*h

S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:

S=a*b

используется в тех случаях, когда сечение идет параллельно двум основаниям.

При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:

S =2R*h

где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.

Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:

S =2а*h

где 2а – значение хорды, расчета площади поперечного сечения.

Источник

From Wikipedia, the free encyclopedia

A cross-section view of a compression seal

In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.

In technical drawing a cross-section, being a projection of an object onto a plane that intersects it, is a common tool used to depict the internal arrangement of a 3-dimensional object in two dimensions. It is traditionally crosshatched with the style of crosshatching often indicating the types of materials being used.

With computed axial tomography, computers can construct cross-sections from x-ray data.

Definition[edit]

If a plane intersects a solid (a 3-dimensional object), then the region common to the plane and the solid is called a cross-section of the solid.^[1] A plane containing a cross-section of the solid may be referred to as a cutting plane.

The shape of the cross-section of a solid may depend upon the orientation of the cutting plane to the solid. For instance, while all the cross-sections of a ball are disks,^[2] the cross-sections of a cube depend on how the cutting plane is related to the cube. If the cutting plane is perpendicular to a line joining the centers of two opposite faces of the cube, the cross-section will be a square, however, if the cutting plane is perpendicular to a diagonal of the cube joining opposite vertices, the cross-section can be either a point, a triangle or a hexagon.

Plane sections[edit]

A related concept is that of a plane section, which is the curve of intersection of a plane with a surface.^[3] Thus, a plane section is the boundary of a cross-section of a solid in a cutting plane.

If a surface in a three-dimensional space is defined by a function of two variables, i.e., z = f(x, y), the plane sections by cutting planes that are parallel to a coordinate plane (a plane determined by two coordinate axes) are called level curves or isolines.^[4]
More specifically, cutting planes with equations of the form z = k (planes parallel to the xy-plane) produce plane sections that are often called contour lines in application areas.

Mathematical examples of cross sections and plane sections[edit]

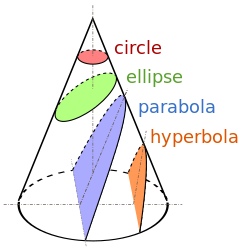
Colored regions are cross-sections of the solid cone. Their boundaries (in black) are the named plane sections.

A cross section of a polyhedron is a polygon.

The conic sections – circles, ellipses, parabolas, and hyperbolas – are plane sections of a cone with the cutting planes at various different angles, as seen in the diagram at left.

Any cross-section passing through the center of an ellipsoid forms an elliptic region, while the corresponding plane sections are ellipses on its surface. These degenerate to disks and circles, respectively, when the cutting planes are perpendicular to a symmetry axis. In more generality, the plane sections of a quadric are conic sections.^[5]

Cross-section of a solid cylinder

A cross-section of a solid right circular cylinder extending between two bases is a disk if the cross-section is parallel to the cylinder’s base, or an elliptic region (see diagram at right) if it is neither parallel nor perpendicular to the base. If the cutting plane is perpendicular to the base it consists of a rectangle (not shown) unless it is just tangent to the cylinder, in which case it is a single line segment.

The term cylinder can also mean the lateral surface of a solid cylinder (see cylinder (geometry)). If a cylinder is used in this sense, the above paragraph would read as follows: A plane section of a right circular cylinder of finite length^[6] is a circle if the cutting plane is perpendicular to the cylinder’s axis of symmetry, or an ellipse if it is neither parallel nor perpendicular to that axis. If the cutting plane is parallel to the axis the plane section consists of a pair of parallel line segments unless the cutting plane is tangent to the cylinder, in which case, the plane section is a single line segment.

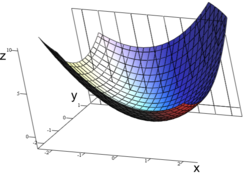
A graph of z = x² + xy + y². For the partial derivative at (1, 1, 3) that leaves y constant, the corresponding tangent line is parallel to the xz-plane.

A plane section of the above graph showing the level curve in the xz-plane at y= 1

A plane section can be used to visualize the partial derivative of a function with respect to one of its arguments, as shown. Suppose z = f(x, y). In taking the partial derivative of f(x, y) with respect to x, one can take a plane section of the function f at a fixed value of y to plot the level curve of z solely against x; then the partial derivative with respect to x is the slope of the resulting two-dimensional graph.

[edit]

A plane section of a probability density function of two random variables in which the cutting plane is at a fixed value of one of the variables is a conditional density function of the other variable (conditional on the fixed value defining the plane section). If instead the plane section is taken for a fixed value of the density, the result is an iso-density contour. For the normal distribution, these contours are ellipses.

In economics, a production function f(x, y) specifies the output that can be produced by various quantities x and y of inputs, typically labor and physical capital. The production function of a firm or a society can be plotted in three-dimensional space. If a plane section is taken parallel to the xy-plane, the result is an isoquant showing the various combinations of labor and capital usage that would result in the level of output given by the height of the plane section. Alternatively, if a plane section of the production function is taken at a fixed level of y—that is, parallel to the xz-plane—then the result is a two-dimensional graph showing how much output can be produced at each of various values of usage x of one input combined with the fixed value of the other input y.

Also in economics, a cardinal or ordinal utility function u(w, v) gives the degree of satisfaction of a consumer obtained by consuming quantities w and v of two goods. If a plane section of the utility function is taken at a given height (level of utility), the two-dimensional result is an indifference curve showing various alternative combinations of consumed amounts w and v of the two goods all of which give the specified level of utility.

Area and volume[edit]

Cavalieri’s principle states that solids with corresponding cross-sections of equal areas have equal volumes.

The cross-sectional area () of an object when viewed from a particular angle is the total area of the orthographic projection of the object from that angle. For example, a cylinder of height h and radius r has $A'=pi r^{2}$ when viewed along its central axis, and A'=2rh when viewed from an orthogonal direction. A sphere of radius r has $A'=pi r^{2}$ when viewed from any angle. More generically, can be calculated by evaluating the following surface integral:

$A'=iint limits _{{mathrm {top}}}d{mathbf {A}}cdot {mathbf {{hat {r}}}},$

where is the unit vector pointing along the viewing direction toward the viewer, is a surface element with an outward-pointing normal, and the integral is taken only over the top-most surface, that part of the surface that is “visible” from the perspective of the viewer. For a convex body, each ray through the object from the viewer’s perspective crosses just two surfaces. For such objects, the integral may be taken over the entire surface () by taking the absolute value of the integrand (so that the “top” and “bottom” of the object do not subtract away, as would be required by the Divergence Theorem applied to the constant vector field ) and dividing by two:

$A'={frac {1}{2}}iint limits _{A}|d{mathbf {A}}cdot {mathbf {{hat {r}}}}|$

In higher dimensions[edit]

In analogy with the cross-section of a solid, the cross-section of an n-dimensional body in an n-dimensional space is the non-empty intersection of the body with a hyperplane (an (n − 1)-dimensional subspace). This concept has sometimes been used to help visualize aspects of higher dimensional spaces.^[7] For instance, if a four-dimensional object passed through our three-dimensional space, we would see a three-dimensional cross-section of the four-dimensional object. In particular, a 4-ball (hypersphere) passing through 3-space would appear as a 3-ball that increased to a maximum and then decreased in size during the transition. This dynamic object (from the point of view of 3-space) is a sequence of cross-sections of the 4-ball.

Examples in science[edit]

Schematic cross-sectional view of the interior of Earth

Cross-section of the midbrain at the level of the superior colliculus.

In geology, the structure of the interior of a planet is often illustrated using a diagram of a cross-section of the planet that passes through the planet’s center, as in the cross-section of Earth at right.

Cross-sections are often used in anatomy to illustrate the inner structure of an organ, as shown at the left.

A cross-section of a tree trunk, as shown at left, reveals growth rings that can be used to find the age of the tree and the temporal properties of its environment.

Notes[edit]

^ Swokowski 1983, p. 296
^ in more technical language, the cross-sections of a 3-ball are 2-balls
^ Albert 2016, p. 38
^ Swokowski 1983, p. 716
^ Albert 2016, p. 117
^ these cylinders are open, they do not contain their bases
^ Stewart 2001, p. 59

References[edit]

Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3
Stewart, Ian (2001), Flatterland / like flatland, only more so, Persus Publishing, ISBN 0-7382-0675-X
Swokowski, Earl W. (1983), Calculus with analytic geometry (Alternate ed.), Prindle, Weber & Schmidt, ISBN 0-87150-341-7

Источник

В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.

Определение величины
Область применения
Способы расчета

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

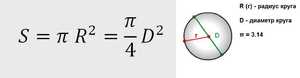
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

Определение объемов емкостей.
Решение задач по сопротивлению материалов и электротехнике.
Расчет количества материалов при проектировании, строительстве и ремонте.
Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

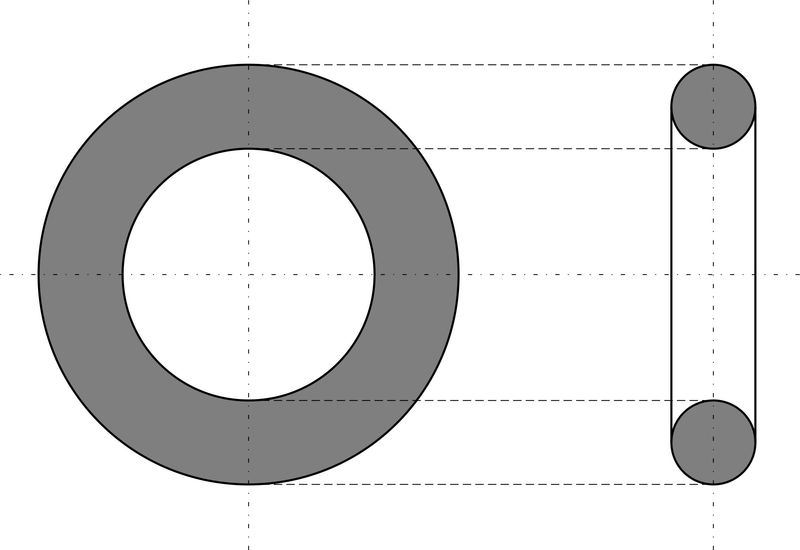
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

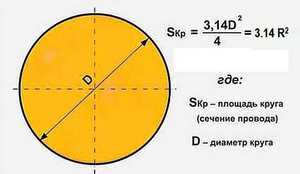
Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Источник