Как найти стороны прямогульника - Сайт, где вы сможете решить свои вопросы

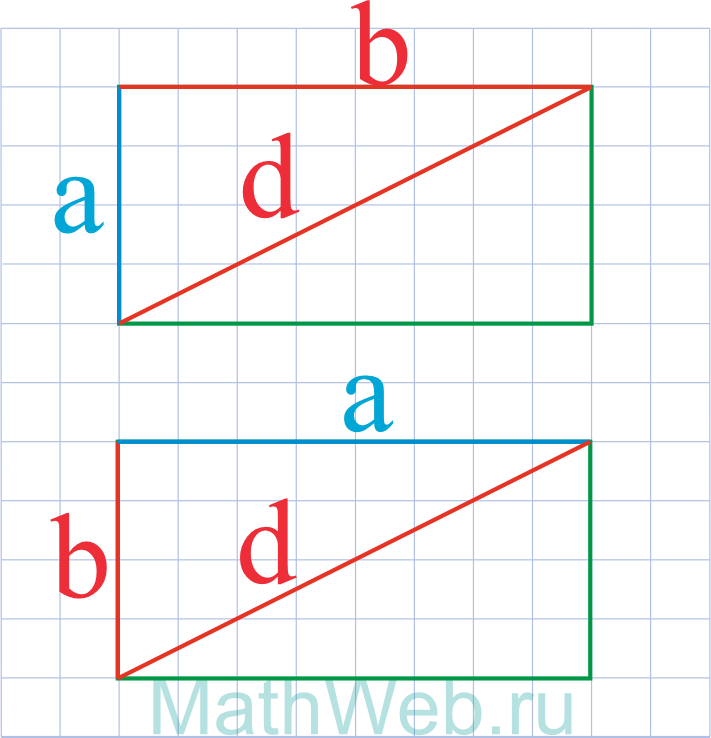
Где d – диагональ,b – сторона.

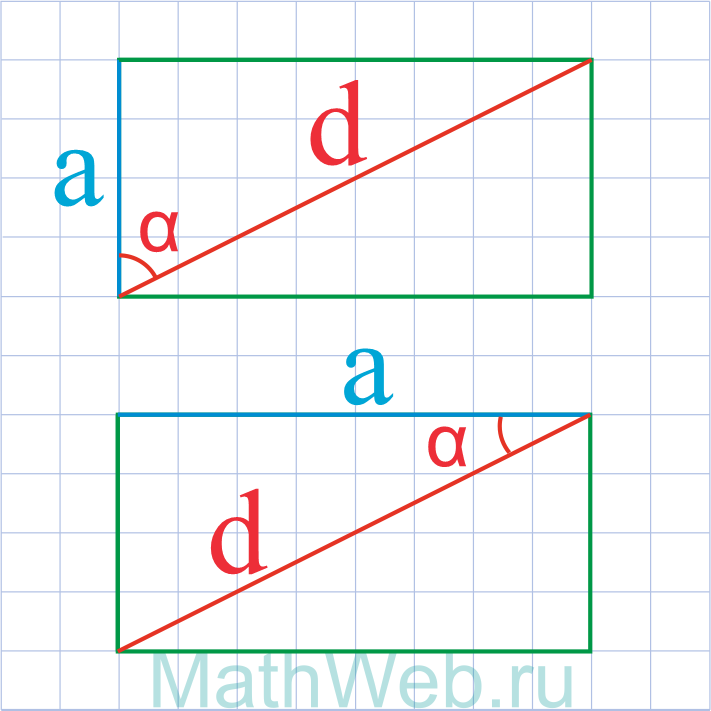
Где d – диагональ,α – угол между диагональю и искомой стороной.

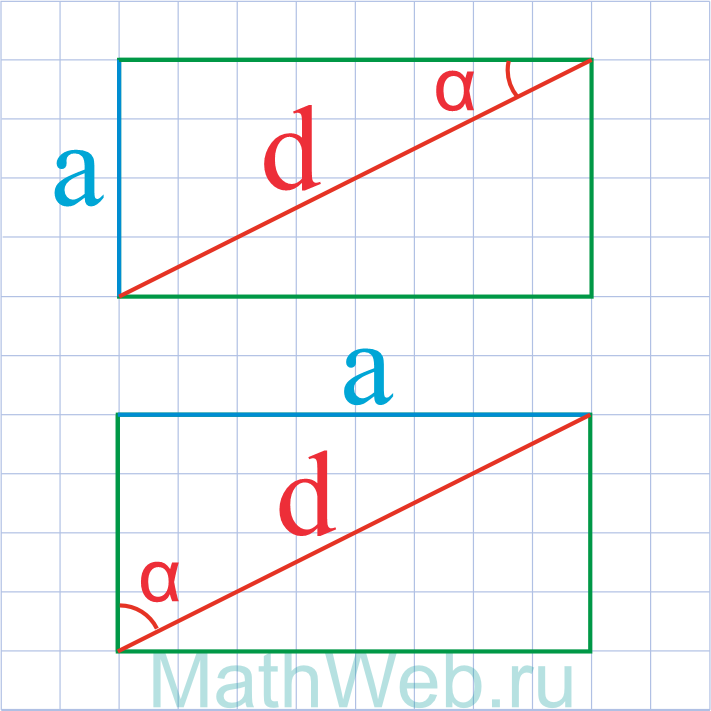
Где d – диагональ,α – угол между диагональю и другой стороной.

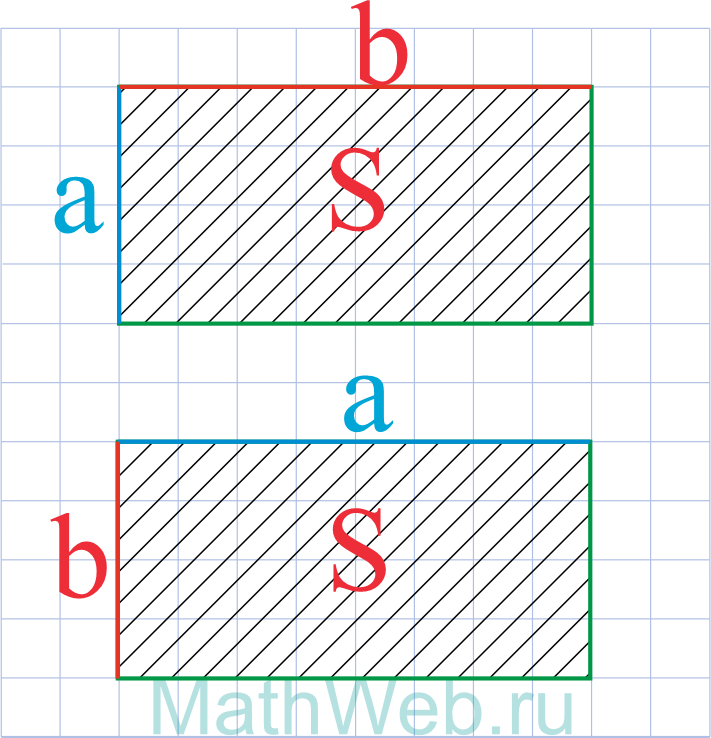
Где S – площадь, b– известная сторона.

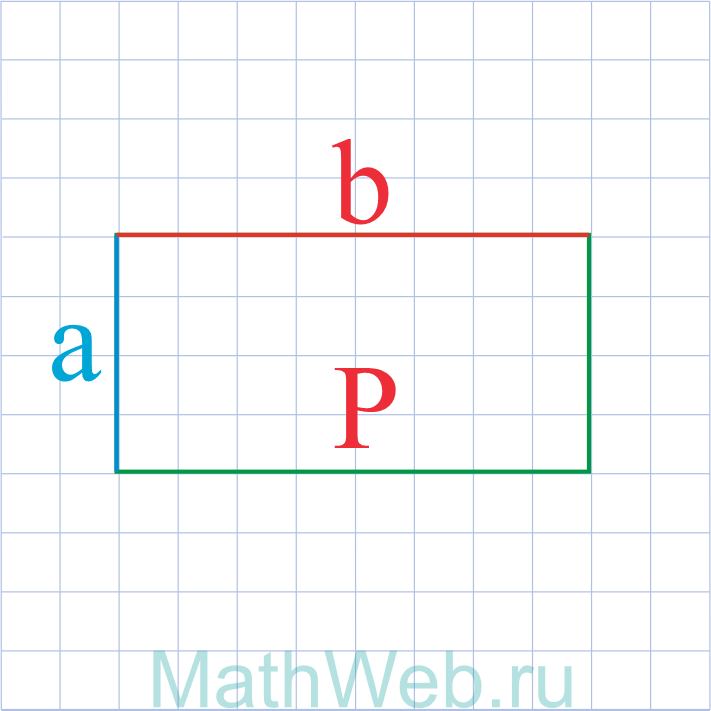
Где P – периметр, b – известная сторона.

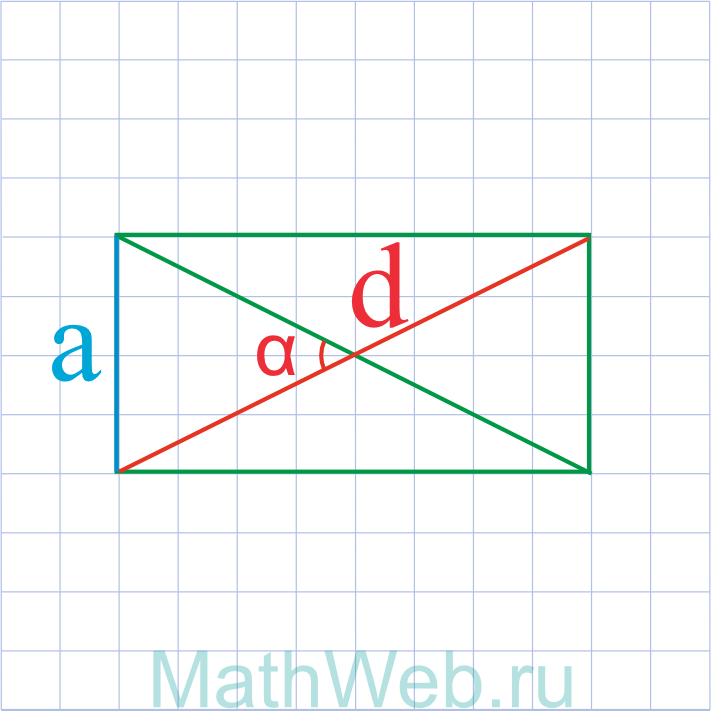
Где d – диагональ, α – угол между диагоналями.

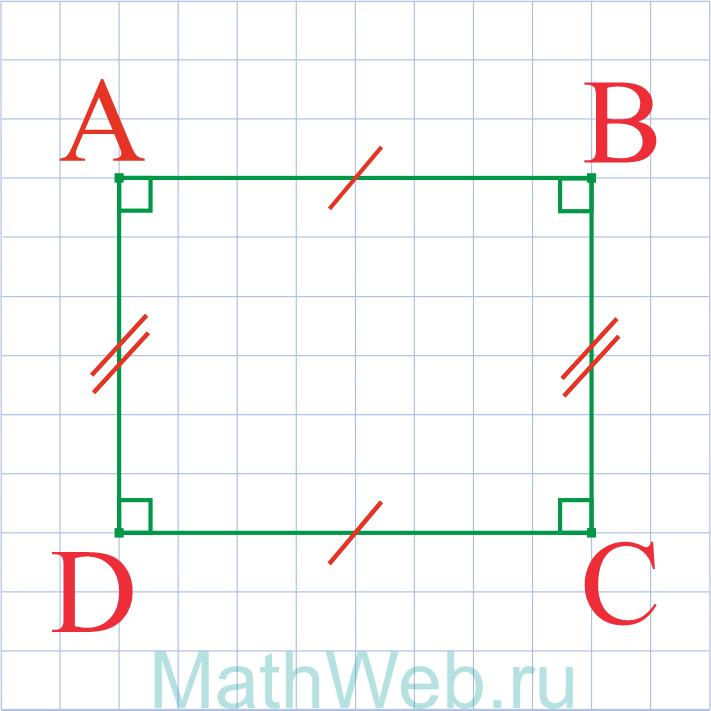
Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
Стороны прямоугольника являются его высотами.
Между прилегающими сторонами угол всегда 90°.

Как найти длину стороны прямоугольника?

Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.

	a = √d² ― b²
	a = d·cos(α)
	a = d·sin(α)
	a = S b
	a = P – 2b 2
	a = d·sin(0.5·α)

Источник

Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла.
Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой.
Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами,
квадрат — это особенный случай прямоугольника.

Сторона прямоугольника через диагональ и угол между
диагональю и стороной
Сторона прямоугольника через диагональ и известную
сторону
Сторона прямоугольника через площадь и другую известную
сторону
Сторона прямоугольника через периметр и другую известную
сторону
Сторона прямоугольника через диагональ и угол между
диагоналями

Через диагональ и угол между диагональю и стороной

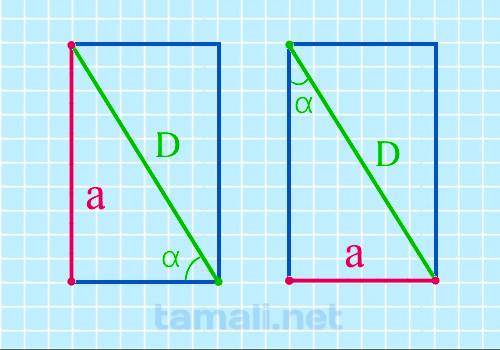
Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол
средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно
воспользоваться следующей формулой:

a = d * sinα

где d — это диагональ, а, b — одна из сторон фигуры.

Цифр после
запятой:

Результат в:

Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой
стороной — 60º.

Решение.
D = 16, β = 60º, b = ?
b = 16 cos 60º
b = 16 * 0.5 = 8 см.

Через его площадь и известную сторону

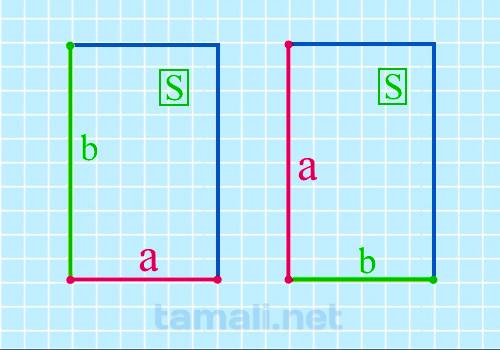
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно

a = S / b

где S — площадь прямоугольника, b — известная сторона.

Цифр после
запятой:

Результат в:

Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем
известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.

Через диагональ и известную сторону

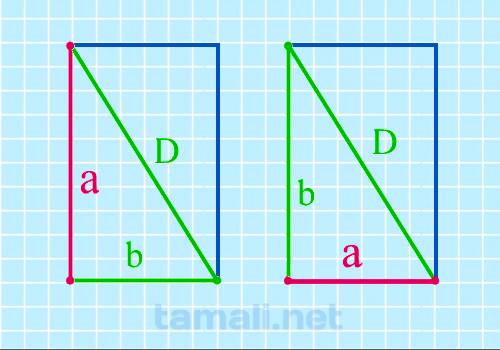
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.
Диагональ
— это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них
разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а
две соседние стороны — остальные стороны треугольника. Отсюда :

a = √(d² — b²)

где d — диагональ, а, b — стороны.

Цифр после
запятой:

Результат в:

Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.

Решение.
D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см.

Через диагональ и угол между диагоналями

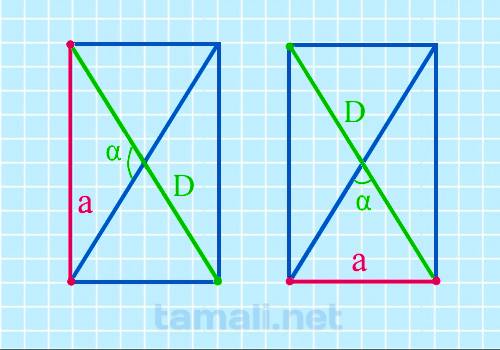
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать
сторону прямоугольника, зная следующую формулу:

a = D • sin(α/2)

где D — диагональ, α — угол между диагоналями.

Цифр после
запятой:

Результат в:

Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти
сторону.

Решение.
a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.

Через периметр и другую известную сторону

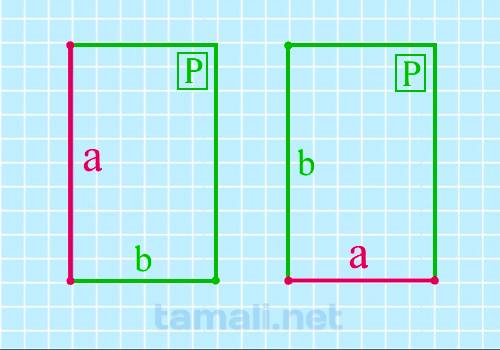
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра
для получения длины. P = 2 (a + b).

a = (P — 2b) / 2

где P — периметр прямоугольника, b — другая известная сторона.

Цифр после
запятой:

Результат в:

Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4).Вычислив,
получим 12 см.

Другие примеры по решению задач на прямоугольник с использованием длины и ширины

Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
Результат: P
прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов
Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3
м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы
преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см.
Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см².
Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти
периметр прямоугольника. Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17,
используем теорему Пифагора и составим уравнение: AB² +AD² =BD².
Получаем: х² +(х+7)² =17² ⇒ х² +х² +14х+49=289; 2х² +14х-240=0; х² +7х-120=0,
отсюда по теореме Виета х1 =-15; х2 =8.Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника: P = 2∙ (AB+AD); P = 2∙ (8+15); P = 46 см.
Ответ: 46 см.

Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены
ниже.

Прямоугольник — это четырехугольник.
Противоположные стороны прямоугольника являются равными и параллельны друг другу.
Внутренний угол прямоугольника при каждой вершине равен 90°.
Сумма внутренних углов равна 360°.
Диагонали пересекаются друг с другом.
Длина диагоналей равна.
Длина диагоналей может быть получена с помощью теоремы Пифагора. Длина диагонали со сторонами a
и b равна, диагональ = ( a2 + b2).
Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
Все прямоугольники являются параллелограммами, но все параллелограммы не являются
прямоугольниками.

Источник

Площадь – 56 квадратных см. Периметр – 30 см.

Сторона А=7, сторона В=8

S=AxB

P=2A+2B

S=56

P=30

автор вопроса выбрал этот ответ лучшим

Можно попробовать решить данную задачу, составив систему уравнений.

Периметр прямоугольника равен: p=2a+2b;

Площадь прямоугольника равна: s=a*b;

Так как мы знаем периметр и площадь, то сразу подставляем числа:

30=2a+2b;

56=a*b;

Выражаем b через a во втором уравнении:

b=56/a;

И подставляем 56/a вместо b в первое уравнение:

30=2a+2(56/a);

15=a+56/a;

Домножаем обе части на a:

15a=a²+56;

Получаем квадратное уравнение:

a²-15a+56=0;

Находим корни этого квадратного уравнения:

(15±√(15²-4*1*56))/2*1 = (15±√(225-224))/2 = (15±√1)/2 = (15±1)/2

Получилось, что корни этого уравнения:

a1=(15+1)/2=16/2=8;

a2=(15-1)/2=14/2=7;

Получается, что у нас 2 возможных варианта прямоугольников.

Вспомним, что мы выразили: b=56/a;

Отсюда находим возможные b:

b1=56/a1=56/8=7;

b2=56/a2=56/7=8;

Как оказалось эти два разных прямоугольника – это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно:

Если a=7 и b=8.

Либо наоборот: a=8 и b=7.

То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот – горизонтальная больше вертикальной.

Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.

Oleg74
[202K]

9 лет назад

Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны :

а – одна сторона, в – другая сторона прямоугольника.

S = а * в

P = 2а + 2в

Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см.

а = 7 см в = 8 см.

Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее

S = а*b

P = 2(а+b)

получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади

Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот.

Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться

если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник;

если дискриминант равен нолю – тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5);

если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 – решения нет)

Galina7v7
[120K]

7 лет назад

Дано: S = 56 см

Р = 30 см

Стороны=?

Решение:

Пусть стороны прямоугольника a и b.

Тогда: площадь S = a * b , периметр Р=2*(a + b),

Получим систему уравнений:

{a*b=56 ? {ab=56

{2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение:

b=15-a, a^2 -15a +56 =0 ,решая которое ,получим :

a1=7, a2=8,

b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7.

Zolotynka
[551K]

7 лет назад

Нашла еще такое решение,

Известно, что периметр прямоугольника 30 а площадь 56, далее:

периметр = 2*(длина + ширина) или 2L + 2W

площадь= длина * ширина или L * W

2L + 2W = 30 (делим обе части на 2)

L + W = 15

L * W = 56

L * (15 – L) = 56

Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется.

Azamatik
[55.3K]

7 лет назад

Вспоминаем школьную геометрию:

Периметр прямоугольника – это будет сумма длин всех сторон, а площадь прямоугольника – это уже произведение двух смежных его сторон (длину на ширину).

В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно.

Итак, решение:

S – площадь = а x b;

56 = a x b;

Р – периметр = а + b + a + b = 2a + 2b;

30 = 2 (а + b);

15 = a + b;

a = 15 – b;

Делаем подставление:

56 = (15 – b) x b;

56 = 15 b – b^2;

b^2 – 15b + 56 = 0.

Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7.

Находим и другую сторону прямоугольника:

a1 = 15 – 8 = 7;

a2 = 15 – 7 = 8.

Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см.

Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь.Это выглядит так А=S/В=56/В

Затем подставляем это выражение вместо буквы А в уравнении для периметра:

Р=2(56/В + В)=30

Получаем что 56/В+В=15

В этом уравнении даже решать его не надо – любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника.

Хеленочка
[61.9K]

8 лет назад

Обозначим одну сторону буквой Х, другую – буквой Y.

Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение:

Х*Y=56

Периметр – это сумма длин сторон, следовательно, второе уравнение такое:

2Х+2Y=30

Получаем систему двух уравнений.

По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение:

2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8.

Lilechka
[36.5K]

9 лет назад

Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения:

(а+c)х2=30

ахс=56

Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см.

moreljuba
[62.5K]

7 лет назад

Итак, для начала рассмотрим формулы для нахождения площади и периметра:

1) S = a * b = 56 см2;

2) Р = 2а + 2b = 30 см.

Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны.

Таким образом нам требуется решить систему из двух уравнений:

a * b = 56

2а + 2b = 30

Отсюда получаем, что одна сторона равна 7, а другая 8.

Знаете ответ?

Источник

Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.

Расчет длины стороны прямоугольника через диагональ и сторону
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d² = a² + b², а сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон:

2d² = 2a² + 2b²

где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:

a = √d² — b²

b = √d² — a²

где d — диагональ, а, b — стороны прямоугольника.

Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:

Р = 2a + 2b = 2 (а + b)

Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:

a = (P — 2b) / 2

b = (P — 2a) / 2

Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.

Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:

S = аb

Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:

a = S / b

b = S / a

где S — площадь прямоугольника, a, b — его стороны.

Источник

4.4

Средняя оценка: 4.4

Всего получено оценок: 200.

4.4

Средняя оценка: 4.4

Всего получено оценок: 200.

В этой статье мы разберем в подробностях, как найти каждую из сторон прямоугольника. Посмотрим, какие ситуации возможны в задачах и разберем самые трудные и интересные из задач.

Длины прямоугольника

Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.

Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.

Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:

Диагонали прямоугольника равны.
Диагонали точкой пересечения делятся пополам.
Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.

Рис. 1. Прямоугольник

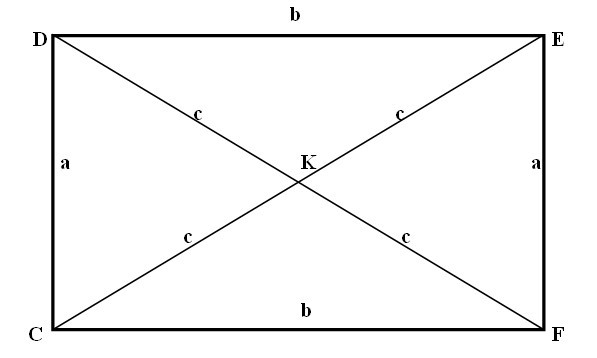
Примеры решения задач

Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.

Задача 1

Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.

Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:

$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)

$a*b=S$ (уравнение для нахождения площади)

При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.

Продолжим решение. Выразим значение a из первого выражения системы.

$(а+b)*2=Р$
$а+b={Рover{2}}$
$а={Рover{2}}-b$
Подставим значение периметра: $а={20over{2}}-b=10-b$

Подставим получившееся выражение в уравнение нахождения площади:

$a*b=S$

$(10-b)*b=21$

$b^2-10b-21=0$

Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.

$а=10-b$

Значит, при $b=3$, $а=10-3=7$

При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.

Задача 2

Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.

Рис. 2. Рисунок к задаче.

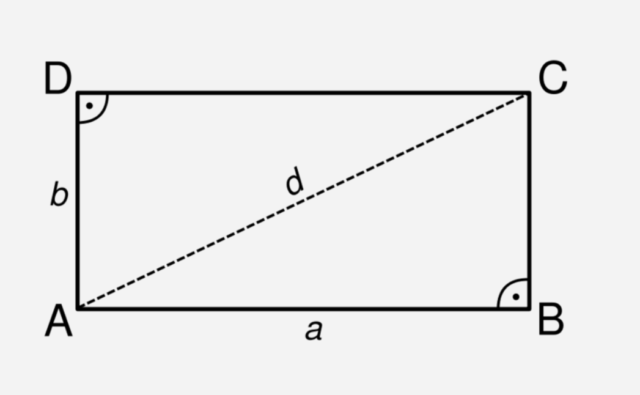
Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).

Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.

$D^2=a^2+b^2$

$A^2=d^2-b^2$

$а^2=400-256=144$

Корень квадратный из 144 равен 12. Это и есть ответ к задаче.

Задача 3

Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.

Рис. 3. Квадрат.

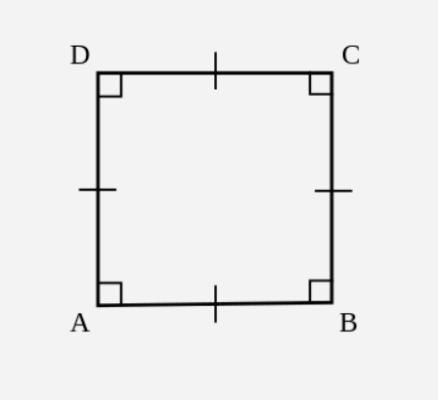
У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.

Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.

$а^2=S$

$а^2=25$

$а=5$

Что мы узнали?

Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 200.

А какая ваша оценка?

Источник

Как найти длину стороны прямоугольника?

Через диагональ и угол между диагональю и стороной

Через его площадь и известную сторону

Через диагональ и известную сторону

Через диагональ и угол между диагоналями

Через периметр и другую известную сторону

Другие примеры по решению задач на прямоугольник с использованием длины и ширины

Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.

Дано: S = 56 см

Р = 30 см

Стороны=?

Решение:

Длины прямоугольника

Примеры решения задач

Задача 1

Задача 2

Задача 3

Что мы узнали?

Тест по теме

Оценка статьи

Вам также может понравиться

Как найти свой ник в сампе

Как в ворде найти функцию заменить

Как вы нашли работу после университета

Добавить комментарий Отменить ответ