|
Как найти отношение сторон прямоугольника?Помоги себе сам 4 года назад
Эта задачка для семиклассника. Но мы ведь с Вами учились дольше! Задачу решить просто даже для семиклассника. Сначала нужно произвести анализ условия и определить алгоритм достижения цели. Нужно найти соотношение сторон. Но соотношение должно быть выражено в числовых величинах. Для этого нужно узнать размеры сторон АВ и ВС. Известно количество равных прямоугольников, из которых состоит прямоугольник ABCD. Известно, что в прямоугольнике противоположные стороны равны между собой. Еще у нас есть число 7, которое будет частью ответа. Думаю, что решение понятно. Успехов! Кстати, задача решается, как говорят, в уме, числового ответа не даю, потому что нужно понять и получить знания для решения подобных задач.
в избранное
ссылка
отблагодарить Вл50 Ответ выдали, но на чертеже нет обозначений сторон малых прямоугольников. Поэтому обойдемся без иксов и игреков. ВС = AD
Гэндальф 4 года назад Обозначим короткую сторону маленького прямоугольника “х”, а длинную его сторону “у”. Тогда АВ = х + у, ВС = 4х, а АД = 3у. Но так как ВС=АД, то 4х = 3у. Отсюда находим х = 3у/4. Подставим этот икс в полученное выше уравнение АВ = х + у, получим АВ = 3у/4 + у = 7у/4. Теперь находим соотношение искомое АВ/ВС. АВ = 7у/4, ВС = 3у. Поэтому соотношение будет АВ/ВС = 7у/4 / 3у. Делим одну дробь на другую, сокращаем игреки и получаем, что соотношение равно 7/12. комментировать
в избранное
ссылка
отблагодарить Евгений трохов 4 года назад Рассмотрим стороны ВС и АД .Так вот,если принять длинную сторону маленького прямоугольника за 1, то другая меньшая сторона будет равна 3/4.Теперь найдём соотношение АВ/ВС=(1+3/4)/(4*(3/4)=7/12.Можно и по другому.У нас ВС=АД.Тогда АВ/ВС=АВ/АД=(1+(3/4))/3=7/12.Ответ-7/12 комментировать
в избранное
ссылка
отблагодарить габбас 4 года назад Обозначим стороны маленького прямоугольника через х и у. Тогда АВ = х+у, ВС = 4*у. По рисунку видно, что 4*у = 3*х, то есть х = (4*у)/3. Получим АВ = (4*у)/3 +у = (7*у)/3. Значит искомое отношение АВ:ВС = (7*у)/3 : 4*у = 7/12. Ответ: 7:12.
в избранное
ссылка
отблагодарить Вл50 Нужно решить без X и Y.
SIlm В седьмом классе не знают решение задачи подстановкой неизвестного?
Видно, что соотношение стороне маленьких прямоугольников составляет 3/4, а тогда соотношение сторон большого прямоугольника составит (3+4)/(3+3+3+3), или 7/12 комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Школьная математика » Блог » Как найти стороны прямоугольника при известных периметре и площади
В этой статье я хочу рассмотреть две математические задачи повышенной сложности для 4 класса.
Видеоурок по теме этой статьи можно посмотреть по ссылке.
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
С этими задачами, я уверен, без труда справится более старший школьник, знакомый с решением системы уравнений и квадратных уравнений. Кстати, подобная задача есть в учебнике по геометрии Атанасяна, глава VI № 454 пункт б за 8 класс.
Но почему же эти задачи указаны в математических сборниках как задачи для 4 класса, в котором еще не изучают алгебраические понятия и методы решения? Нет ли здесь ошибки?
Нет, никакой ошибки здесь нет. Эти, и аналогичные им задачи можно решить и без использования алгебраических знаний.
Первое, что приходит на ум – это по значению периметра прямоугольника (а периметр – это удвоенная сумма двух его сторон) найти сумму двух сторон, а после простым подбором определить два числа, произведение которых равно данной по условию площади прямоугольника, а сумма – половине периметра.
Я хочу показать вам математически точное решение, которое безо всяких подборов приводит к правильному результату.
Нахождение сторон прямоугольника при известных периметре и площади
Рассмотрим первую задачу:
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Как известно, периметр прямоугольника находится по формуле ({color{red} P=2cdot (a+b)}) , площадь – по формуле ({color{red} S=acdot b}) .
Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:
({color{red} a + b = 24 : 2 = 12}) см.
А дальше мы рассуждаем так.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной ({color{red} 12 : 2 = 6}) см.
Тогда площадь этого квадрата равна
({color{red}S_{k}=6cdot 6=36}) см2.
По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.
({color{red} S–S _{k}=36-32=4}) см2.
Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.
Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.
Но на какое?
Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.
Тогда, ширина искомого прямоугольника будет равна:
({color{red} a=6-2=4}) см
а длина:
({color{red} b=6+2=8}) см.
Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:
({color{red} P=2cdot (4+8)=2cdot 12=24}) см
({color{red} S=4cdot 8=32}) см2.
Задача решена верно.
Теперь рассмотрим вторую задачу.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
Находим полупериметр, то есть, сумму двух сторон прямоугольника.
({color{red} a+b=46:2=23}) см.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. ({color{red} 23=11+12}).
Площадь такого прямоугольника равна:
({color{red}S_{2}=11cdot 12=132}) см2.
Разница между полученной площадью и заданной по условию задачи составляет:
({color{red}S_{2}-S=132-126=6}) см2.
6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.
Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.
Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).
Находим ширину искомого прямоугольника:
({color{red} a=11-2=9}) см.
Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:
({color{red} b=12+2=14}) см.
Проведем проверку:
({color{red} P=2cdot (9+14)=2cdot 23=46}) см.
({color{red}S=9cdot 14=126}) см2.
И эта задача решена тоже верно.
На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.
Вам также пригодится:
Как найти стороны прямоугольника, зная его площадь и отношение
Прямоугольник – это двумерная геометрическая фигура с двумя парами противоположных сторон, каждая из которых образует прямой угол. Если известна площадь и отношение сторон (ширины и длины) прямоугольника, то можно найти длину и ширину.
Формула для нахождения сторон прямоугольника
Площадь прямоугольника (S) равна произведению его длины (a) и ширины (b):
$$S = ab$$
Отношение длины к ширине (k) прямоугольника – это какое-то число (k), которое показывает, насколько длиннее длина, чем ширина:
$$k = frac{a}{b}$$
Отсюда можно выразить длину (a) через ширину (b):
$$a = kb$$
Подставляя это выражение в формулу для площади прямоугольника можно получить уравнение, которое позволит найти ширину (b):
$$S = kb^2$$
$$b = sqrt{frac{S}{k}}$$
Для нахождения длины (a) необходимо подставить найденное значение для ширины (b) в уравнение:
$$a = ksqrt{frac{S}{k}} = sqrt{Sk}$$
Таким образом, для нахождения сторон прямоугольника по его площади и отношению длины к ширине нужно:
- Вычислить ширину прямоугольника по формуле:
$$b = sqrt{frac{S}{k}}$$
- Вычислить длину прямоугольника по формуле:
$$a = sqrt{Sk}$$
Заключение
Теперь вы знаете, как найти стороны прямоугольника, зная его площадь и отношение длины к ширине. Эта формула будет полезна при решении задач, связанных с нахождением неизвестных размеров прямоугольника.
Как найти стороны, если известны диагональ и периметр
Если в условиях задачи указан периметр прямоугольника, длина его диагонали, и требуется найти длину сторон прямоугольника, используйте свои знания о способах решения квадратных уравнений и свойствах прямоугольных треугольников.

Инструкция
Обозначьте для удобства стороны прямоугольника, которые необходимо найти в задаче, например, a и b. Диагональ прямоугольника назовите с, а периметр Р.
Составьте уравнение для нахождения периметра прямоугольника, он равен сумме его сторон. У вас получится:
a+b+a+b=Р или 2*а+2*b=Р.
Обратите внимание на тот факт, что диагональ прямоугольника делит его на два равных прямоугольных треугольника. Теперь вспомните, что сумма квадратов катетов равна квадрату гипотенузы, то есть:
а^2+b^2=с^2.
Выпишите рядом полученные уравнения, вы увидите, что получилась система из двух уравнений с двумя неизвестными а и b. Подставьте значения, данные в задаче для величины периметра и диагонали. Предположим, что в условиях задачи значение периметра составляет 14, а гипотенуза 5. Таким образом, система уравнений выглядит следующим образом:
2*а+2*b=14
а^2+b^2=5^2 или а^2+b^2=25
Решите систему уравнений. Для этого в первом уравнении перенесите b со множителем в правую часть и разделите обе части уравнения на множитель а, то есть на 2. Вы получите:
а=7-b
Подставьте значение а во второе уравнение. Правильно раскройте скобки, помните о том, как возводить в квадрат слагаемые в скобках. Вы получите:
(7-b)^2+b^2=25
7^2-7*2*b+ b^2+b^2=25
49-14*b+2*b^2=25
2*b^2-14*b+24=0
Вспомните свои знания о дискриминанте, в этом уравнении он равен 4, то есть больше 0, соответственно, данное уравнение имеет 2 решения. Вычислите корни уравнения с помощью дискриминанта, вы получите, что сторона прямоугольника b равна либо 3, либо 4.
Подставьте поочередно полученные значения стороны b в уравнение для а (смотрите шаг 5), а=7-b. Вы получите, что при b равном 3, а равно 4. И наоборот, при b равном 4, а равно 3. Обратите внимание, что решения симметричны, поэтому ответ задачи таков: одна из сторон равна 4, а вторая 3.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Где d – диагональ,b – сторона.
Где d – диагональ,α – угол между диагональю и искомой стороной.
Где d – диагональ,α – угол между диагональю и другой стороной.
Где S – площадь, b– известная сторона.
Где P – периметр, b – известная сторона.
Где d – диагональ, α – угол между диагоналями.
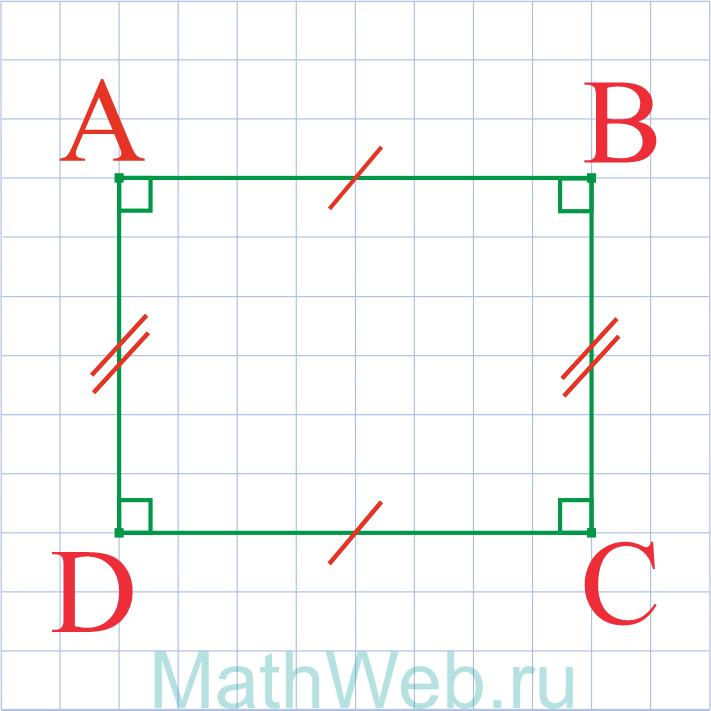
- Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
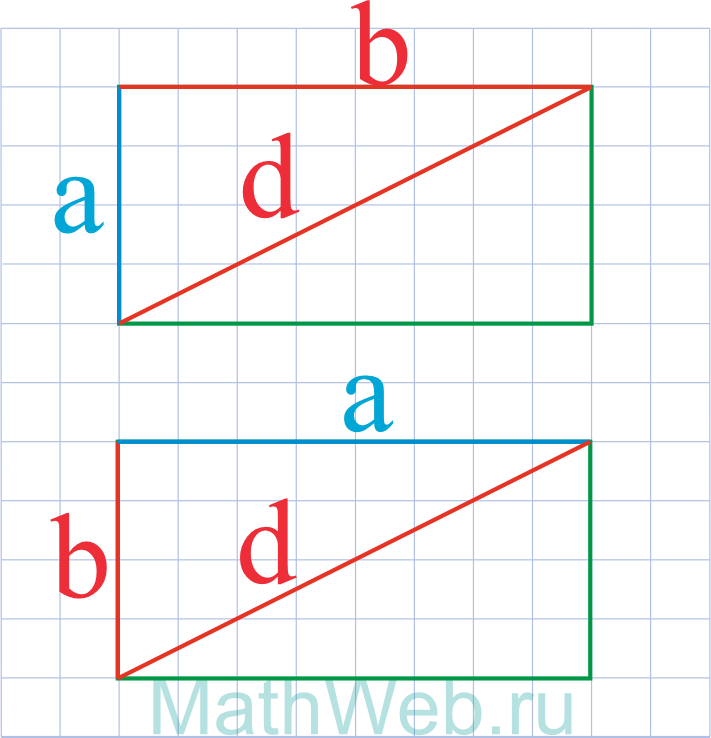 |
a = √d2 ― b2 |
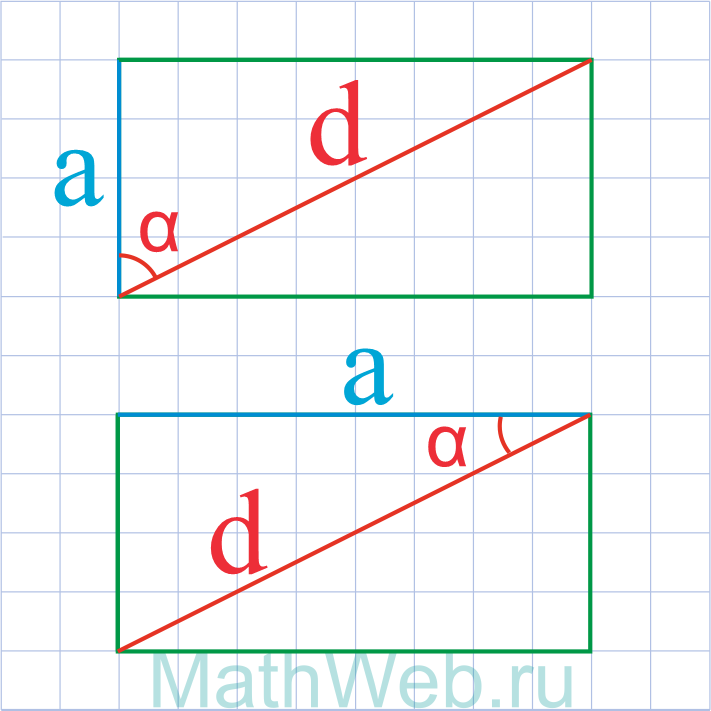 |
a = d·cos(α) |
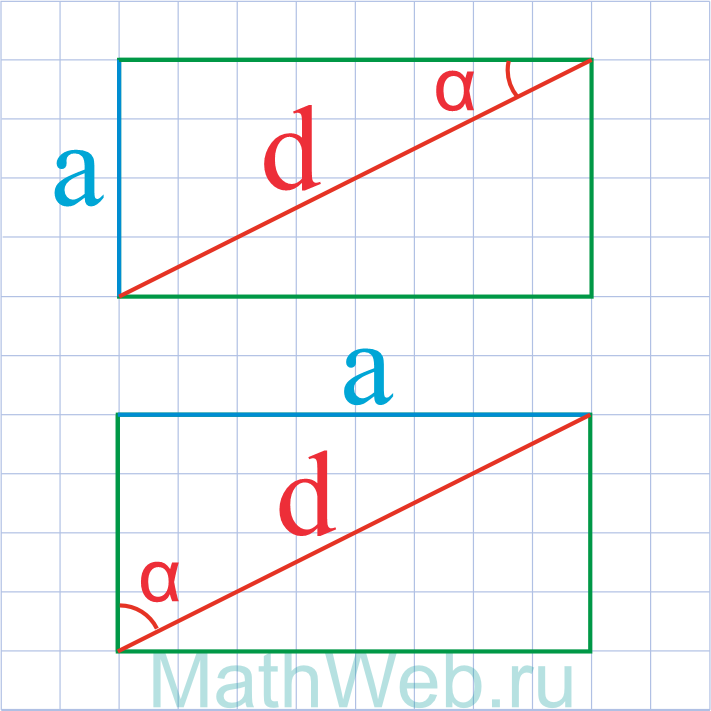 |
a = d·sin(α) |
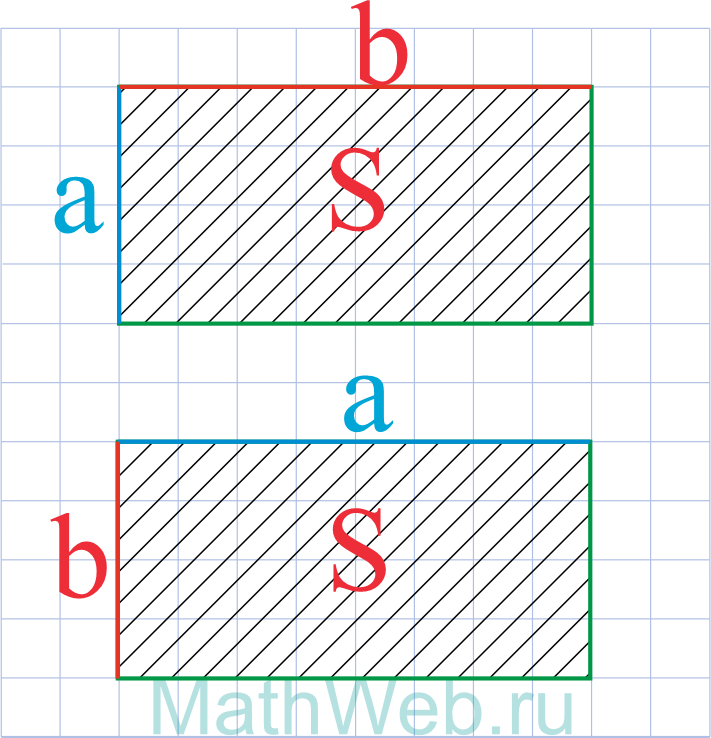 |
a = S b |
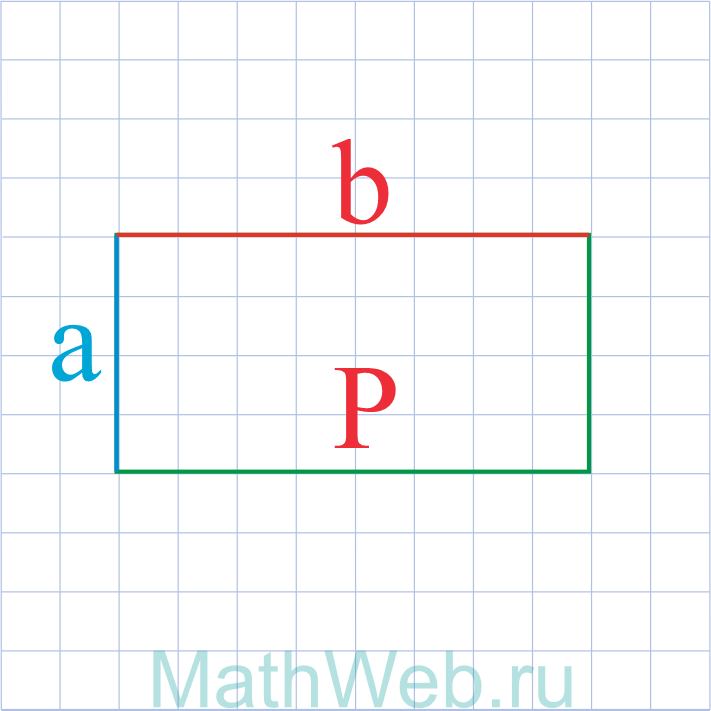 |
a = P – 2b 2 |
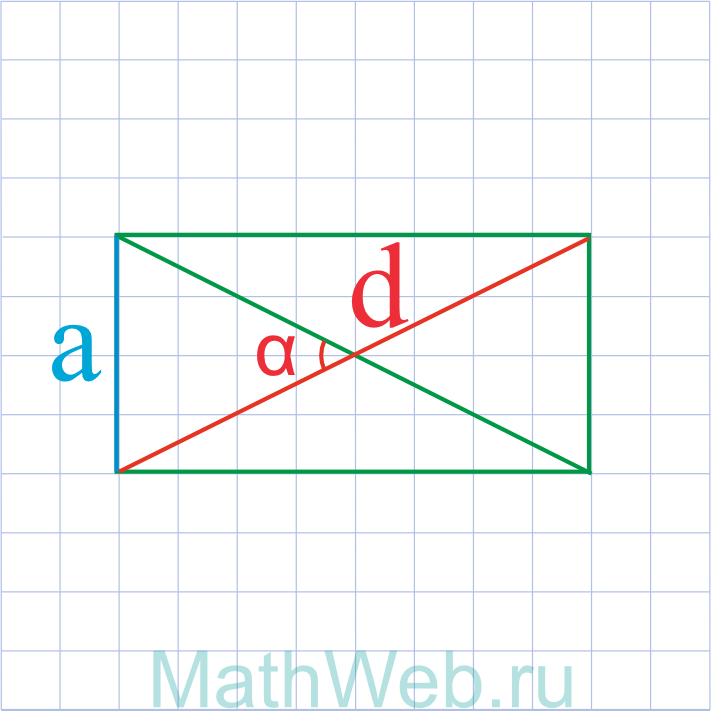 |
a = d·sin(0.5·α) |