Длина стороны правильного многоугольника
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Правильный пятиугольник — построение, свойства и формулы
Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.

Точное построение фигуры
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:
Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.
Алгоритм Биона
Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.
Приближенные методы
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).
Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.
Расчет параметров
С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.
Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.
Условные обозначения
Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:
Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).
Соотношения и формулы
После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:
Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:

Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:
Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:

Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.
Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).
Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.
Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
[spoiler title=”источники:”]
http://sprint-olympic.ru/uroki/geometrija/85022-pravilnyi-piatiygolnik-postroenie-svoistva-i-formyly.html
[/spoiler]
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
-
Расчет длины стороны
-
Через радиус вписанной окружности
- Через радиус описанной окружности
-
Через радиус вписанной окружности
Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Через радиус вписанной окружности
Формула расчета
![]()
Через радиус описанной окружности
Формула расчета
![]()
Пятиугольник, виды, свойства и формулы.
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник, выпуклый и невыпуклый пятиугольник
Правильный многоугольник
Свойства правильного пятиугольника
Построение правильного пятиугольника
Формулы правильного пятиугольника
Правильный пятиугольник в природе, технике и культуре
Пятиугольник, шестиугольник, семиугольник, восьмиугольник
Пятиугольник, выпуклый и невыпуклый пятиугольник:
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).
Пятиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый пятиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 540°.

Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.

Рис. 2. Невыпуклый пятиугольник
Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.
Правильный многоугольник:
Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.

Рис. 3. Правильный пятиугольник
Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.
Свойства правильного пятиугольника:
1. Все стороны правильного пятиугольника равны между собой.
a1 = a2 = a3 = a4= a5.
2. Все углы равны между собой и каждый угол равен 108°.
α1 = α2 = α3 = α4 = α5 = 108°.

Рис. 4. Правильный пятиугольник
3. Сумма внутренних углов правильного пятиугольника равна 540°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.

Рис. 5. Правильный пятиугольник
5. Количество диагоналей правильного пятиугольника равно 5.

Рис. 6. Правильный пятиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр пятиугольника O.

Рис. 7. Правильный пятиугольник
7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.

Рис. 8. Правильный пятиугольник
8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
a / c ≈ 5 / 8 ≈ 0,618.

Рис. 9. Правильный пятиугольник
Построение правильного пятиугольника:
Метод построения правильного пятиугольника вписыванием его в заданную окружность:
1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.
Формулы правильного пятиугольника:
Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.
Формулы площади правильного пятиугольника:

Формулы высоты правильного пятиугольника:

Формулы стороны правильного пятиугольника:

Формулы диагонали правильного пятиугольника:

Формулы радиуса окружности, вписанной в правильный пятиугольник:

Формулы радиуса окружности, описанной вокруг правильного пятиугольника:

Правильный пятиугольник в природе, технике и культуре:
Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.
Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.
Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Пятиугольник
Шестиугольник
Семиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
9 547
Правильный пятиугольник
Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.
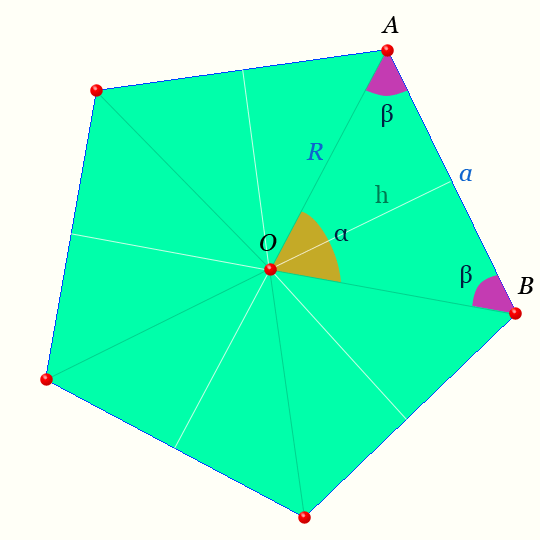
Правильный пятиугольник
Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного пятиугольника.
Обозначения на рисунке для правильного пятиугольника
| n=5 | число сторон и вершин правильного пятиугольника, | шт |
|---|---|---|
| α | центральный угол правильного пятиугольника, | радианы, ° |
| β | половина внутреннего угла правильного пятиугольника, | радианы, ° |
| γ | внутренний угол правильного пятиугольника, | радианы, ° |
| a | сторона правильного пятиугольника, | м |
| R | радиусы правильного пятиугольника, | м |
| p | полупериметр правильного пятиугольника, | м |
| L | периметр правильного пятиугольника, | м |
| h | апофемы правильного пятиугольника, | м |
Основные формулы для правильного пятиугольника
Периметр правильного пятиугольника
[ L = 5a ]
Полупериметр правильного пятиугольника
[ p = frac{5}{2}a ]
Центральный угол правильного пятиугольника в радианах
[ α = frac{2}{5}π ]
Центральный угол правильного пятиугольника в градусах
[ α = frac{360°}{5} = 72° ]
Половина внутреннего угла правильного пятиугольника в радианах
[ β = frac{3}{10}π ]
Половина внутреннего угла правильного пятиугольника в градусах
[ β = frac{3}{10}180° = 54° ]
Внутренний угол правильного пятиугольника в радианах
[ γ = 2β = frac{3}{5}π ]
Внутренний угол правильного пятиугольника в градусах
[ γ = frac{3}{5}180° = 108° ]
Площадь правильного пятиугольника
[ S = ph = frac{5}{2}ha ]
Или учитывая формулу Площади правильного пятиугольника получим
[ S = frac{5}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]
Отсюда получим апофему правильного пятиугольника
[ h = sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]
Правильный пятиугольник |
стр. 269 |
|---|
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
![]()
Определение длины стороны правильного многоугольника по радиусу описанной окружности
Радиус описанной окружности
Число сторон правильного многоугольника
Точность вычисления
Знаков после запятой: 2
Длина стороны правильного многоугольника
P.S. В комментариях некто Александр поинтересовался, а как же найти длину стороны по радиусу вписанной окружности?
Отвечаю — с вписанной окружностью все гораздо проще. Надо рассмотреть треугольник, образованный перпендикуляром к точке касания окружности и многоугольника, половиной стороны многоугольника и линией от центра окружности до ближайшей к перпендикуляру вершины многоугольника. Этот треугольник перпендикулярный, и острый угол его равен 360, деленное на число вершин правильного многоугольника и еще пополам. Половина длины стороны находится легко — это радиус (прилежащий катет), умноженный на тангенс острого угла. Домножаем затем на два — получаем искомую длину стороны. Результат — ниже.
![]()
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
Радиус вписанной окружности
Число сторон правильного многоугольника
Точность вычисления
Знаков после запятой: 2
Длина стороны правильного многоугольника
