Как найти стороны шестиугольника 5 класс

План урока:

Понятие правильного многоугольника

Описанная и вписанная окружности правильного многоугольника

Формулы для правильного многоугольника

Построение правильных многоугольников

Понятие правильного многоугольника

У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.

Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.

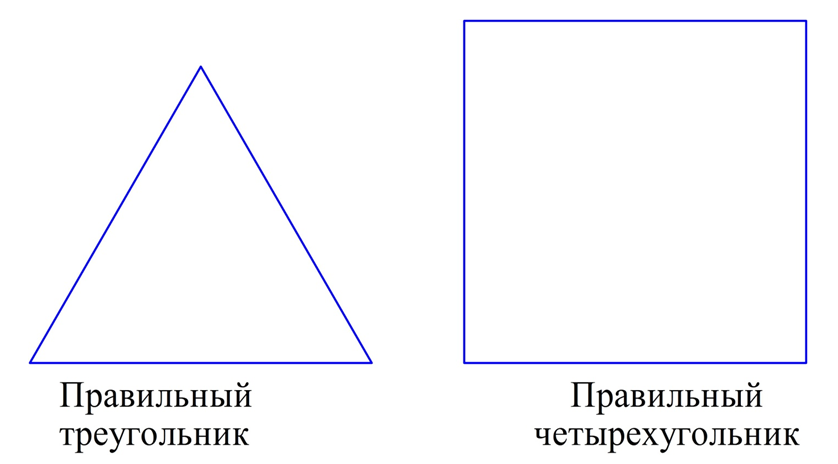
Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.

Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:

Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:

Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:

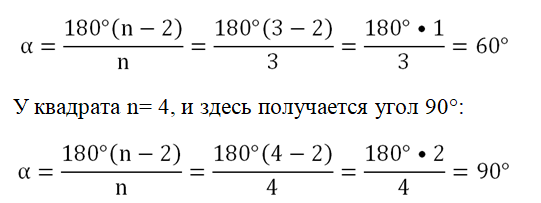
Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?

Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:

Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?

Решение. В формулу 

Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?

Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:

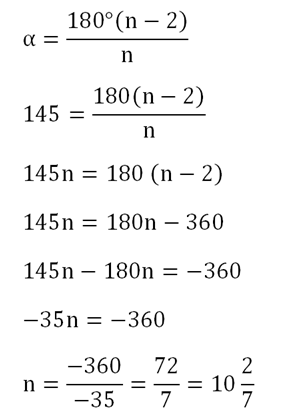
Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.

Ответ: не может.

Описанная и вписанная окружности правильного многоугольника

Докажем важную теорему о правильном многоуг-ке.

Для доказательства обозначим вершины произвольного правильного n-угольника буквами А₁, А₂, А₃…А_n. Далее проведем биссектрисы углов ∠А₁ и ∠А₂. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА₃, ОА₄ и т. д.

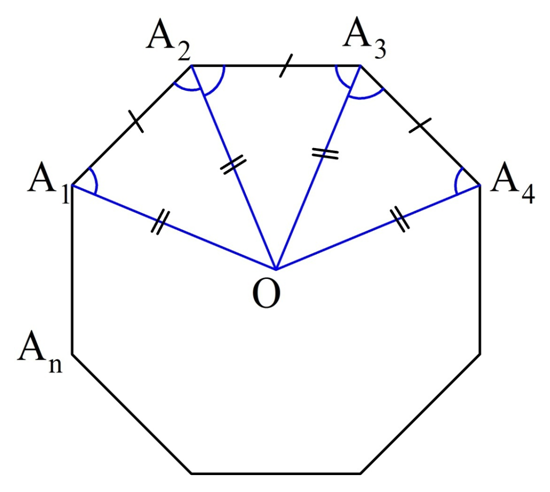
∠А₁ и ∠А₂ одинаковы по определению правильного многоуг-ка:

Из этого факта вытекает два равенства:

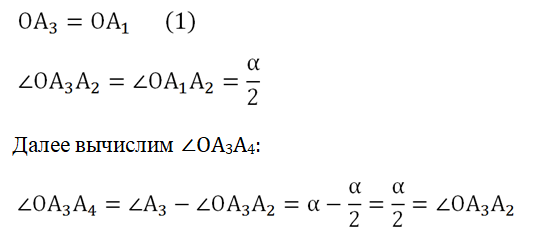
Получается, что ОА₃ – это также биссектриса ∠А₃. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):

Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:

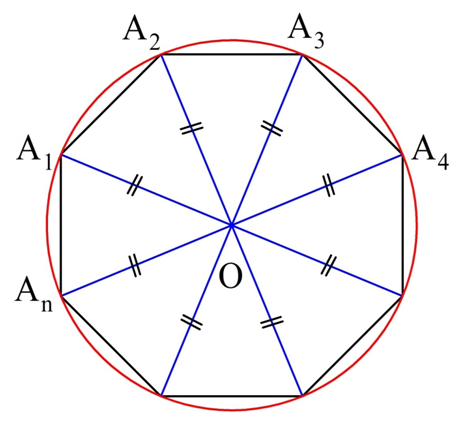
Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А₁, А₂ и А₃, можно провести только одну окружность, ч. т. д.

Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН₁, ОН₂, ОН₃… на стороны многоуг-ка.

Так как высоты проведены в равных треуг-ках, то и сами они равны:

Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН₁. Он должен будет пройти и через точки Н₂, Н₃, … Н_n. Причем отрезки ОН₁, ОН₂, ОН₃ окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:

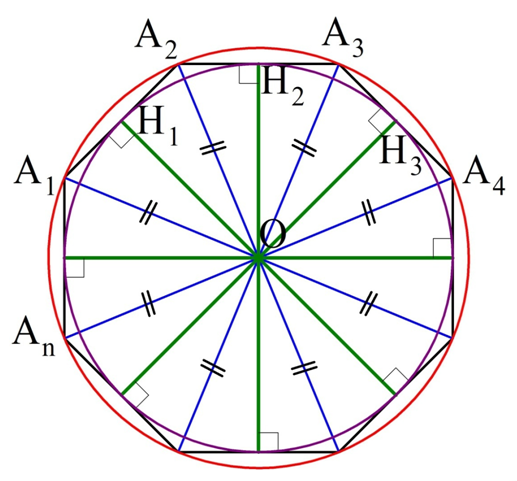
Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А₁, ∠А₂, ∠А₃, то есть в точке О. Так как расстояние от О до А₁А₂ – это отрезок ОН₁, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.

Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.

Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН₁, ОН₂, ОН₃,… проведены в равнобедренных треуг-ках∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н₁, Н₂, Н₃,… – это середины сторон многоуг-ка.

Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?

Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.

Ответ: не могут.

Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.

Формулы для правильного многоугольника

Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой a_n, где n– число сторон у многоуг-ка. Например a₄– это сторона квадрата, a₆– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.

Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу

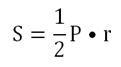
для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.

Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:

Теперь можно найти и ∠А₁ОН₁, рассмотрев ∆А₁ОН₁:

Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:

С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).

Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.

Решение. Запишем следующую формулу:

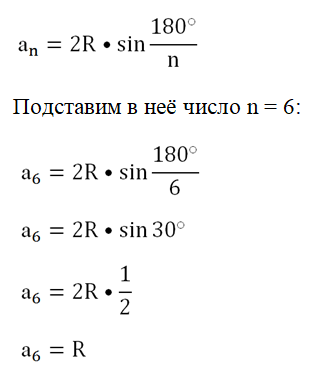
Это равенство как раз и надо было доказать в этом задании.

Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.

Решение. Запишем формулу:

Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.

Решение.

Найдем периметр шестиугольника:

Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?

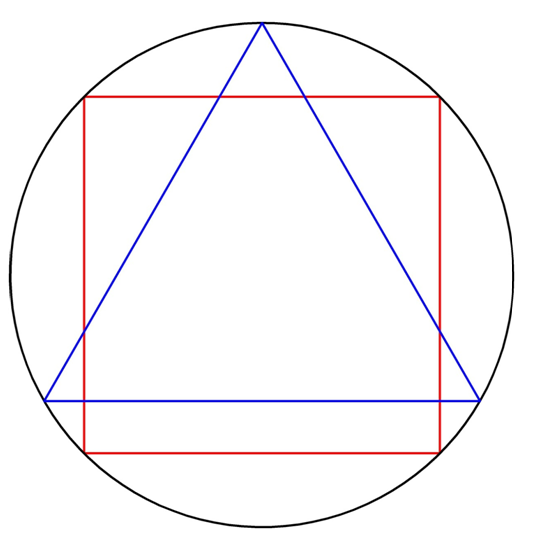
Решение. Зная периметр треуг-ка, легко найдем и его сторону:

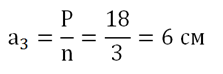
Далее вычисляется радиус описанной около треугольника окружности:

Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?

Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:

Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:

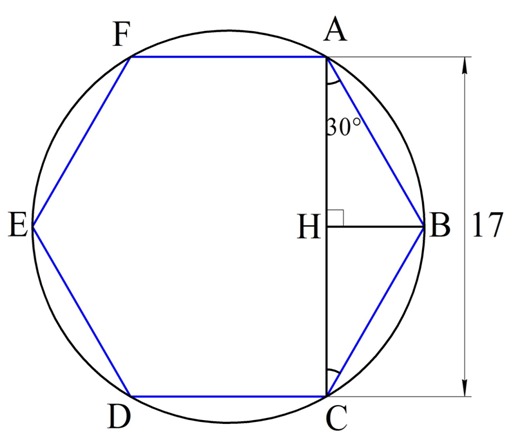
Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:

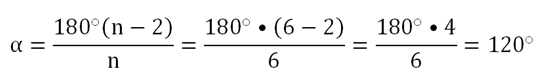
В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:

Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:

AC = 17 мм

∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:

AH = AC/2 = 17/2 = 8,5 мм

Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:

Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.

Ответ: 20 мм.

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.

Как найти сторону правильного шестиугольника

Шестиугольную – «гексагональную» – форму имеют, например, сечения гаек и карандашей, пчелиных сот и снежинок. Правильные геометрические фигуры такой формы имеют некую особенность, отличающую их от прочих плоских многоугольников. Заключается она в том, что радиус описанной около гексагона окружности равен длине его стороны – во многих случаях это значительно упрощает вычисление параметров многоугольника.

Инструкция

Если в условиях задачи дан радиус (R) описанной около правильного шестиугольника окружности, вычислять ничего не придется – эта величина тождественна длине стороны (t) гексагона: t = R. При известном диметре (D) просто поделите его пополам: t = D/2.

Периметр (Р) правильного шестиугольника позволяет вычислить длину стороны (t) простой операцией деления. В качестве делителя используйте число сторон, т.е. шестерку: t = Р/6.

Радиус (r) вписанной в такой многоугольник окружности связан с длиной его стороны (t) немного более сложным коэффициентом – удвойте радиус, а полученный результат разделите на квадратный корень из тройки: t = 2*r/√3. Эта же формула с использованием диаметра (d) вписанной окружности станет на одно математическое действие короче: t = d/√3. Например, при радиусе в 50 см длина стороны шестиугольника должна быть приблизительно равна 2*50/√3 ≈ 57,735 см.

Известная площадь (S) многоугольника с шестью вершинами тоже позволяет вычислить длину его стороны (t), но численный коэффициент, связывающий их, точно выражается через дробь из трех натуральных чисел. Две трети площади делите на квадратный корень из тройки, а из полученного значения извлекайте квадратный корень: t = √(2*S/(3*√3)). Например, если площадь фигуры составляет 400 см², длина ее стороны должна составлять примерно √(2*400/(3*√3)) ≈ √(800/5,196) ≈ √153,965 ≈ 12,408 см.

Длина окружности (L), описанной около правильного шестиугольника, связана с радиусом, а значит и с длиной стороны (t) через число Пи. Если он дана в условиях задачи, поделите ее величину на два числа Пи: t = L/(2*π). Скажем, если эта величина равна 400 см, длина стороны должна составлять приблизительно 400/(2*3,142) = 400/6,284 ≈ 63,654 см.

Этот же параметр (l) для вписанной окружности позволяет рассчитать длину стороны шестиугольника (t) вычислением соотношения между ней и произведением числа Пи на квадратный корень из тройки: t = l/(π*√3). Например, если длина вписанной окружности составляет 300 см, сторона шестиугольника должна иметь величину, примерно равную 300/(3,142*√3) ≈ 300/(3,142*1,732) ≈ 300/5,442 ≈ 55,127 см.

Видео по теме

Источники:

• сторона шестиугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Шестиугольник, виды, свойства и формулы.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник, выпуклый и невыпуклый шестиугольник

Правильный шестиугольник (понятие и определение)

Свойства правильного шестиугольника

Формулы правильного шестиугольника

Правильный шестиугольник в природе, технике и культуре

Звездчатый шестиугольник

Восьмиугольник

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

  Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

.

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6  сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆. 

2. Все углы равны между собой и составляют 120°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

R = a

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

 

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

R = a

Звездчатый шестиугольник:

Звездчатый шестиугольник (гексаграмма) – это многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника.

Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
7 491

Правильный шестиугольник: свойства, формулы, площадь

Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.

Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.

Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?

Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.

Мы знаем, что площадь правильного треугольника: .

Тогда площадь правильного шестиугольника — в шесть раз больше.

, где — сторона правильного шестиугольника.

Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.

Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.

Ты нашел то, что искал? Поделись с друзьями!

. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .

. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

Сторона правильного шестиугольника. Калькулятор и формулы

Определить сторону правильного шестиугольника можно легко при помощи этого калькулятора. Просто заполните любую ячейку, введя известное вам значение, – и под калькулятором отобразятся значения всех недостающих величин, а также формулы их нахождения. Это удобная шпаргалка по геометрии, которую полезно всегда держать под рукой!

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Правильный шестиугольник и его свойства

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

Замечание

Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;

каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

Теорема

Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]

Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: (a=R) .

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны (120^circ) .

4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

Замечание

В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .

[spoiler title=”источники:”]

http://calcon.ru/storona-pravilnogo-shestiugolnika-kalkulyator-i-formuly/

http://shkolkovo.net/theory/77

[/spoiler]

Математика

5 класс

Урок №37

Многоугольники

Перечень рассматриваемых вопросов:

– наглядные представления о фигурах на плоскости;

– многоугольники;

– периметр многоугольника;

– выпуклые многоугольники;

– изображение геометрических фигур.

Тезаурус

Многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Периметр многоугольника – это сумма всех его сторон.

Диагональ многоугольника – это отрезок, соединяющий две несмежные вершины многоугольника.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Мы уже знаем, из каких элементов состоят некоторые геометрические фигуры и как их изобразить на плоскости. Сегодня мы рассмотрим многоугольник.

Ломаная линия лежит в основе построения многоугольника.

Построим ломаную. Для этого отметим на плоскости несколько точек – например, пять. Соединим их так, чтобы никакие два из отрезков, имеющих общие точки, не лежали на одной прямой. Полученная фигура и будет ломаной, которую обозначают A, B, C, D, E.

Отрезки АВ, ВС, СD,DE называются звеньями ломаной. У ломаной, которую мы изобразили, четыре звена.

Если измерить длину каждого звена и найти их сумму, то получится длина ломаной.

Измерим длину ломаной.

АВ = 4 см

ВС = 2 см

СD = 3 см

DE = 5 см

Сумма длин всех звеньев равна:

АВ + ВС + СD + DЕ = 14 см – длина ломаной

Теперь нарисуем ломаную таким образом, чтобы её конец совпадал с началом. Получается замкнутая ломаная A, B, C, D, E, А.

Фигуру, образованную таким образом, называют многоугольником. То есть многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Стоит помнить, что многоугольником является как замкнутая линия, так и эта линия вместе с плоскостью внутри неё.

Такие звенья называются сторонами многоугольника. В нашем случае это стороны АВ, ВС, СD,DE, ЕА.

Углы, образованные двумя соседними сторонами, называют углами многоугольника, а их вершины – вершинами многоугольника.

∠А, ∠В, ∠С, ∠D, ∠E – углы многоугольника

Точки А, В, С, D, E – вершины многоугольника

Кроме того, у многоугольника есть ещё и диагонали.

Диагональ – это отрезок, соединяющий две несмежные вершины многоугольника. АС, СЕ – диагонали.

Сумма всех сторон многоугольника составляет периметр многоугольника.

P = АВ + ВС + СD + DЕ + ЕА

Рассмотрим разновидности многоугольников.

Многоугольник называется выпуклым, если он расположен по одну сторону от каждой прямой, содержащей его сторону.

Например, многоугольник ABCDE – выпуклый. А многоугольник MNKLO – нет.

По числу сторон многоугольники делятся на треугольники, пятиугольники и так далее.

Кроме того, многоугольники, у которых все стороны и все углы равны, называют правильными. Например, квадрат.

Многоугольники можно сравнить путём наложения. Если они полностью накладываются друг на друга, то считаются равными. При этом стоит помнить, они имеют одинаковые площади.

Для определения площади многоугольника надо выяснить, сколько раз выбранная единица измерения содержится в этой фигуре.

Не только человек может рисовать многоугольники. Природа тоже создаёт многоугольники в большом разнообразии. Рассмотрим, где они встречаются. Например, шестиугольники можно увидеть в сотах пчёл и – под микроскопом – в строении глаза мухи или некоторых других насекомых.

Панцирь черепахи тоже изобилует большим количеством многоугольников. Как и кожа змеи: она буквально покрыта многоугольниками. В общем, природа постаралась и разнообразила мир геометрическими фигурами.

Тренировочные задания

№ 1. Чему равен периметр правильного шестиугольника со стороной 4 см?

Решение: для решения этой задачи достаточно вспомнить, что в правильных фигурах все стороны равны, следовательно, все стороны шестиугольника равны 4 см. Вычислим периметр шестиугольника, это сумма всех его сторон.

Р = 4 см + 4 см + 4 см + 4 см + 4 см + 4 см = 24 см

Ответ: 24 см.

№ 2. Из листа железа размером 10 × 14 см вырезали два квадрата со стороной 4 см и три прямоугольника со сторонами 2см и 6см. Определите площадь остатка.

Решение: сначала найдём площадь листа:

S = 10 cм · 14 см = 140 см²

Далее вычислим площадь квадратов со сторонами 4см:

S = 4 cм · 4 см = 16 см²

Тогда площадь двух квадратов равна:

16 см²· 2 = 32 см²

Найдём площадь прямоугольника:

S = 2 cм · 6 см = 12 см²

Тогда площадь трёх прямоугольников равна:

12 см²· 3 = 36 см²

Определим площади всех квадратов и прямоугольников, вырезанных из листа:

32 см² + 36 см² = 68 см²

А теперь найдём площадь остатка: 140 см² – 68 см² = 72 см²

Ответ 72 см²