Круги Эйлера
Задача (Простая)
В языке запросов поискового сервера для обозначения логической
операции «ИЛИ» используется символ «|», а для логической
операции «И» — символ «&». В таблице приведены запросы и
количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц (в тысячах) |
|
Пушкин |
3500 |
|
Лермонтов |
2000 |
|
Пушкин | Лермонтов |
4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин
& Лермонтов? Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не изменялся
за время выполнения запросов.
Решение:
Видим, что по запросу “Пушкин” в поисковике нашлось
3500 страниц. По запросу “Лермонтов” – 2000 страниц.
Запрос “Пушкин | Лермонтов” обозначает, что поисковик
выдаст страницы, где есть слова про “Пушкина”, и страницы, где есть
слова про “Лермонтова”, а так же могут быть страницы, где написано и
про “Пушкина”, и про “Лермонтова” одновременно.
Если сложить страницы, в которых написано про
“Пушкина” и про “Лермонтова” получается 3500 + 2000 = 5500
страниц. Но почему же при запросе “Пушкин | Лермонтов” получается
меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про
“Пушкина” (3500 страниц), мы подсчитали и те страницы, где было
написано и про “Пушкина”, и про “Лермонтова” одновременно.
Тоже самое и для количества страниц, где написано про
“Лермонтова” (2000 страниц). В этом числе находятся и те, в которых
одновременно упоминается и про “Пушкина”, и про
“Лермонтова”.
В вопросе спрашивается, сколько страниц будет по запросу “Пушкин
& Лермонтов“. Это обозначает, что как раз нужно найти количество
страниц, где будет одновременно написано и про “Пушкина”, и про
“Лермонтова”.
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) –
4500 = 5500 – 4500 = 1000 страниц.
Теперь решим эту задачу с
помощью Кругов Эйлера!
У нас всего есть две сущности: “Пушкин” и
“Лермонтов”. Поэтому рисуем два пересекающихся круга, желательно
разными цветами.
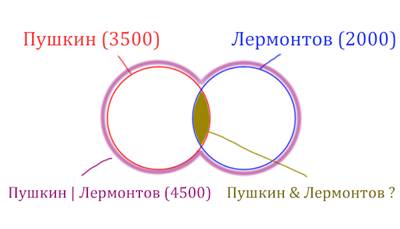
Объединение двух кругов в общую фигуру (показано
фиолетовым цветом), показывает операцию “Пушкин | Лермонтов”. Эта
операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма
площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры,
которая характеризует логическую операцию «ИЛИ» “Пушкин | Лермонтов”
(4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая
закрашена золотистым цветом. Данная логическая операция
«И» стремится уменьшить площадь. Она обозначает общую площадь других
фигур.
Найдём сначала заштрихованную часть синего круга. Она равна:
площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
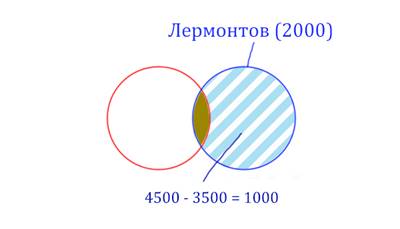
Теперь легко найти площадь золотистой фигуры. Для этого нужно от
площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц)
= 2000 – 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено
1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу из ЕГЭ
по информатике.
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической
операции «ИЛИ» используется символ «|», а для логической операции «И» – символ
«&».
В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц (в тысячах) |
|
Кокос | Ананас |
3400 |
|
Кокос & Ананас |
900 |
|
Кокос |
2100 |
Какое количество страниц (в тысячах) будет найдено по запросу
Ананас?
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за время
выполнения запросов.
Решение:
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера,
которые пересекаются между собой. Так же отменим все имеющееся данные.
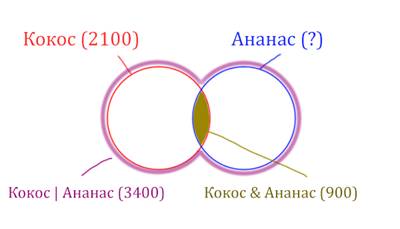
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900.
Заштрихованная часть равна 2100 – 900 = 1200.
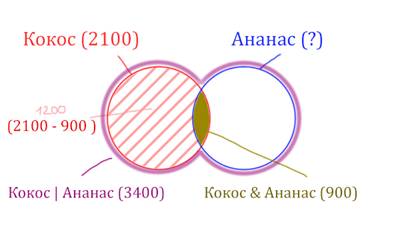
После того, как нашли заштрихованную часть (такой полумесяц),
можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой
фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 – 1200 =
2200
Ответ: 2200
Разберём классическую задачу 17 задания из ЕГЭ по
информатике
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической
операции «ИЛИ» используется символ «|», а для логической операции «И» – символ
«&».
В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц (в тысячах) |
|
(Космос & Звезда) | (Космос & |
1100 |
|
Космос & Планета |
600 |
|
Космос & Планета & Звезда |
50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос
& Звезда?
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за время
выполнения запросов.
Решение:
В этой задаче у нас три сущности: Космос, Планета, Звезда.
Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что
площади по отдельности двух кругов в сумме дают площадь фигуры, которая
получается при применении операции логического “ИЛИ”.
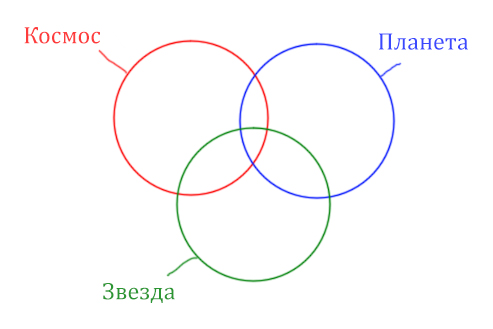
Теперь отметим на нашем рисунке запрос (Космос &
Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках.
Первое Космос & Звезда
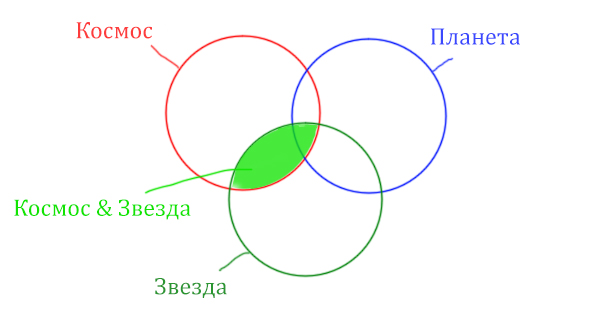
Теперь отметим вторую скобку Космос & Планета.
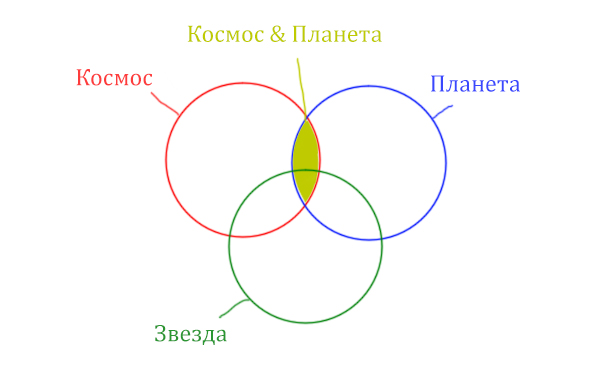
В выражении (Космос & Звезда) | (Космос & Планета) две
скобки соединяет знак логического “ИЛИ”. Значит, эти две области
нужно объединить! Область (Космос & Звезда) | (Космос & Планета)
отмечена фиолетовым цветом!
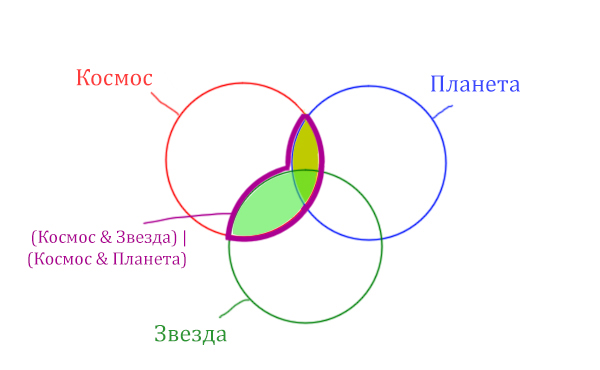
Отметим Космос & Планета ещё раз, т.к. для
этого выражения известно количество страниц.
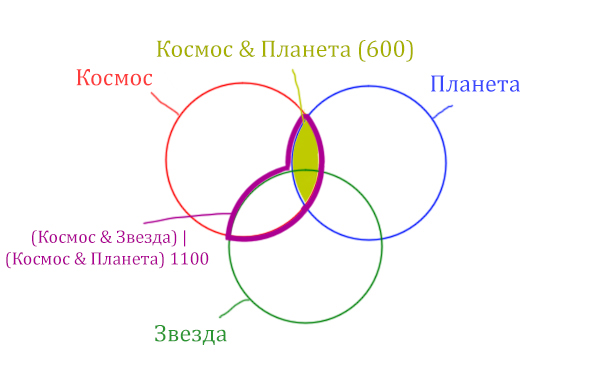
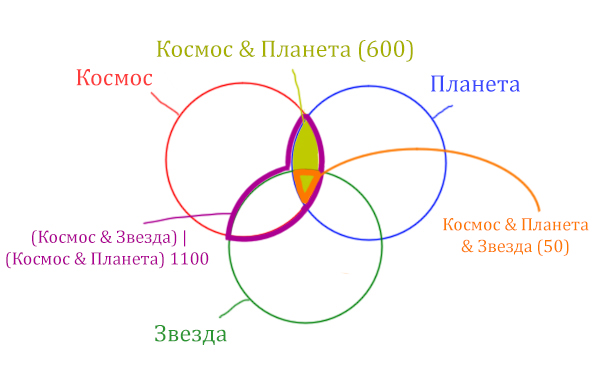
Площадь фигуры для выражения Космос & Планета &
Звезда будет очень маленькая. Это общая часть для всех трёх
кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна
одновременно быть в трёх кругах!
Найти нужно Космос & Звезда. Отменим на рисунке
чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали
салатовым цветом.
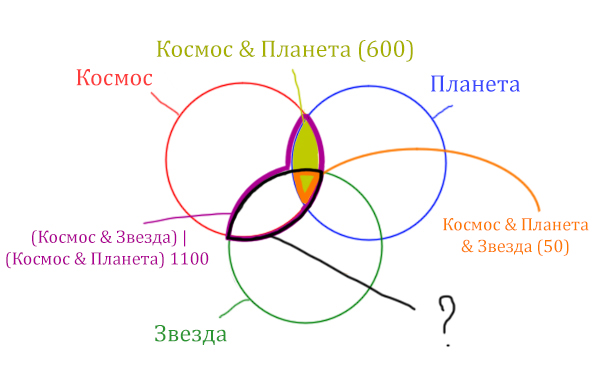
Теперь у нас есть все компоненты, чтобы решить классическую
тренировочную задачу из ЕГЭ по информатике задания 17.
Найдём заштрихованную область.
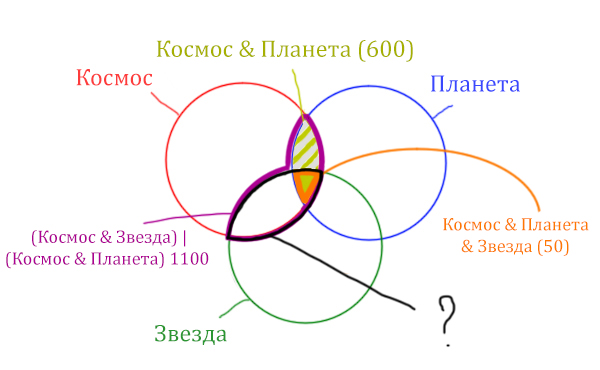
Вся область Космос & Планета равна 600. А
заштрихованная часть равна: область Космос & Планета (600)
минус оранжевая область (50).
Количество страниц в заштрихованной часте =
600 – 50 = 550
Тогда черная область легко находится: фиолетовая область (1100)
минус заштрихованная область (550).
Количество страниц (при запросе Космос
& Звезда) = 1100 – 550 = 550
Ответ: 550
Закрепляем материал при подготовке к 17 заданию ЕГЭ по
информатике
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической
операции «ИЛИ» используется символ «|», а для обозначения логической операции
«И» – символ «&». В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц (в тысячах) |
|
Море & Солнце |
290 |
|
Море & Пляж |
355 |
|
Море & (Пляж | Солнце) |
465 |
Какое количество страниц (в тысячах) будет найдено по запросу
Море & Пляж & Солнце? Считается, что все запросы выполнялись
практически одновременно, так что набор страниц, содержащих все искомые слова,
не изменялся за время выполнения запросов.
Решение:
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому
нарисуем три пересекающихся круга Эйлера.
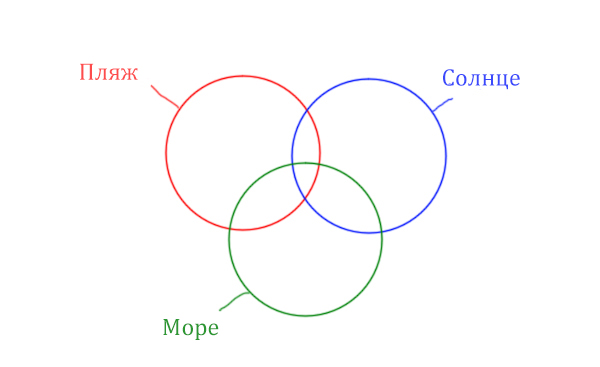
Отметим все области для которых нам даны количество страниц.
В начале отметим Море & (Пляж | Солнце). Для
начало нарисуем область, которая в скобках (Пляж | Солнце)
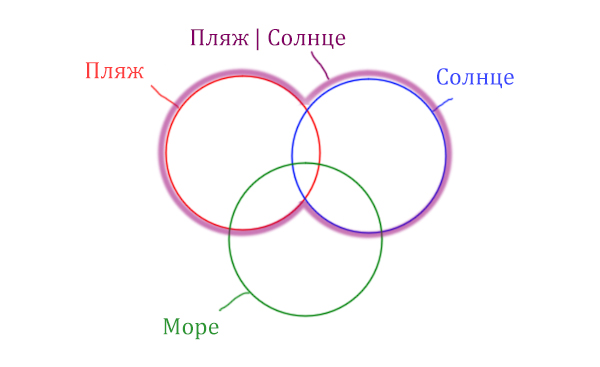
Теперь нужно очертить общую часть фиолетовой области и зелёного
круга и получится Море & (Пляж | Солнце). Отметим оранжевым
цветом.
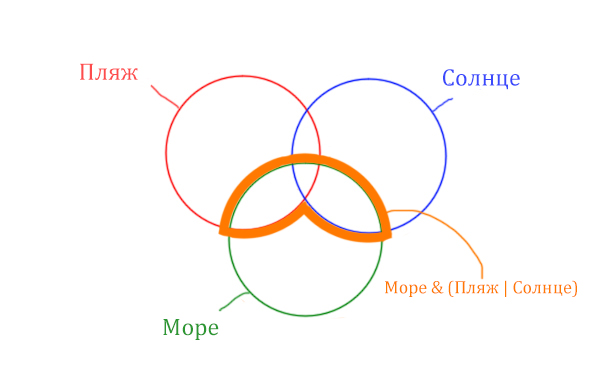
Теперь отметим Море & Пляж.
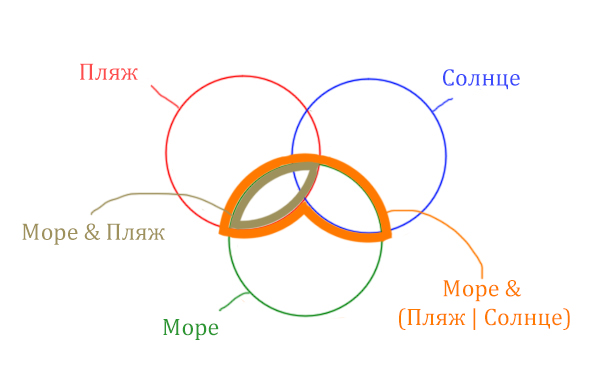
Теперь отметим Море & Солнце.
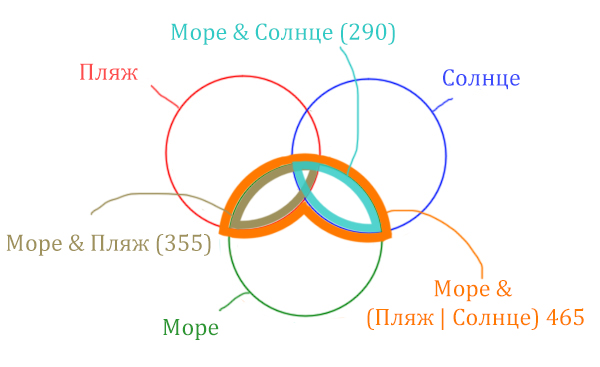
Найти нужно ту область, которая получается в результате
выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
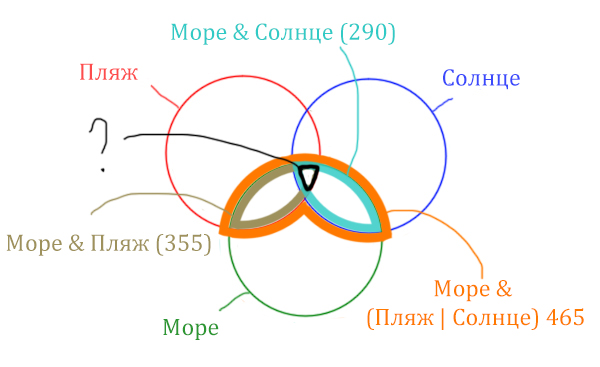
Найдём заштрихованную область!
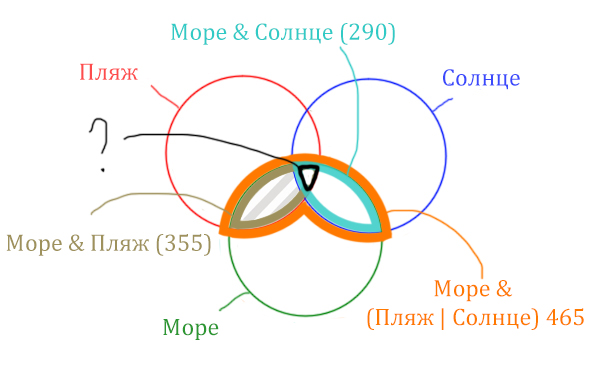
Количество страниц (в заштрихованной
области) =
= Количество страниц (В оранжевой области) – Море & Солнце =
= 465 – 290 = 175
Чтобы найти искомую чёрную область, нужно из Море &
Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж &
Солнце) =
= Море & Пляж (355) – Количество страниц (в заштрихованной
области) 175 =
= 355 – 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу 17 задания из ЕГЭ по
информатике с 4-мя сущностями!
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической
операции «ИЛИ» используется символ «|», а для обозначения логической операции
«И» – символ «&».
В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц (в тысячах) |
|
Англия & (Уэльс & Шотландия | Ирландия) |
450 |
|
Англия & Уэльс & Шотландия |
213 |
|
Англия & Уэльс & Шотландия & |
87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за время
выполнения запросов.
Решение:
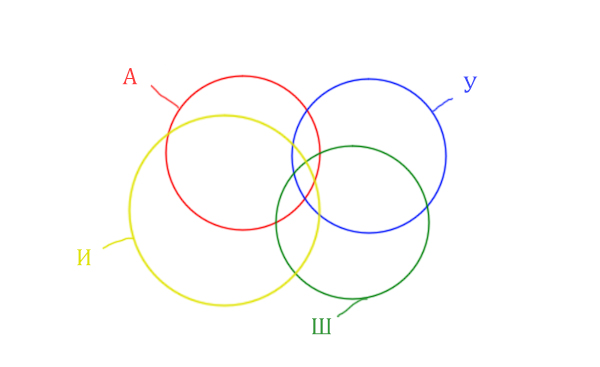
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три
круга, как обычно, оставив немного места для четвёртого круга.
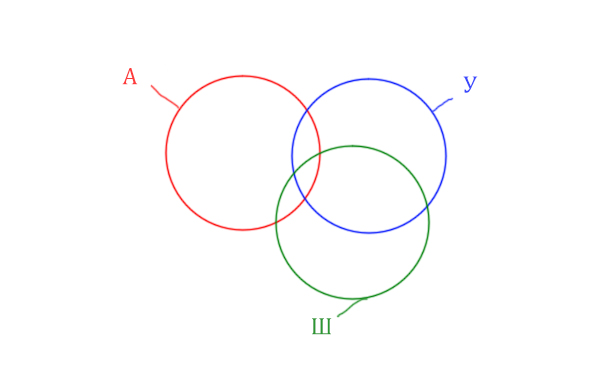
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он
проходил через область (Англия & Уэльс & Шотландия). Это нам
подсказывает сама таблица, где есть количество страниц для Англия & Уэльс
& Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
Нужно отметить на рисунке Англия & (Уэльс &
Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
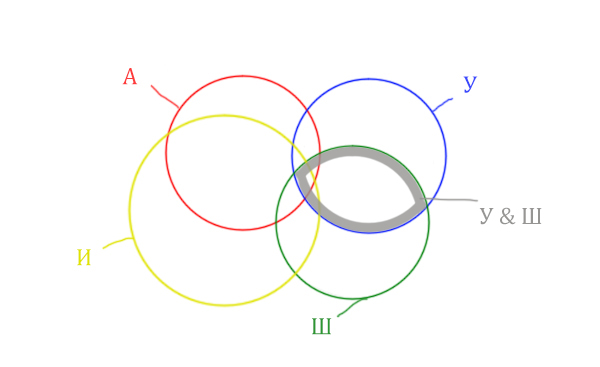
Добавим к этой области Ирландию через логическое
“ИЛИ”. Получается область (Уэльс & Шотландия | Ирландия).
Произошло объединение серой области и жёлтого круга!
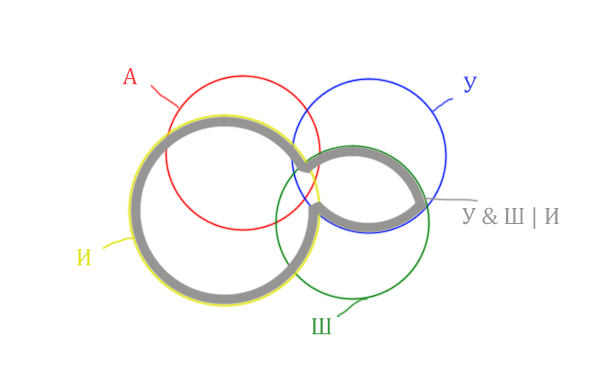
Теперь нужно сделать операцию логического “И”
получившийся области с “Англией”. Тогда область Англия &
(Уэльс & Шотландия | Ирландия) примет вид:
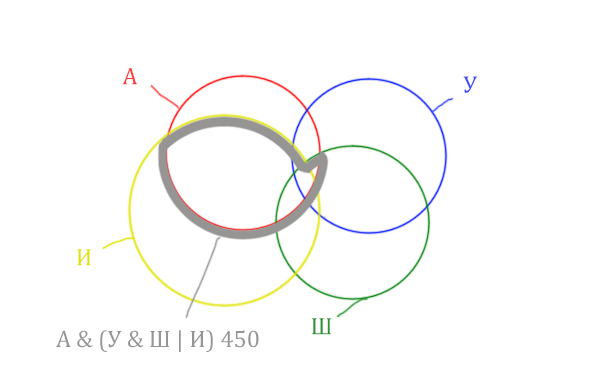
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия –
это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено
оранжевым цветом.
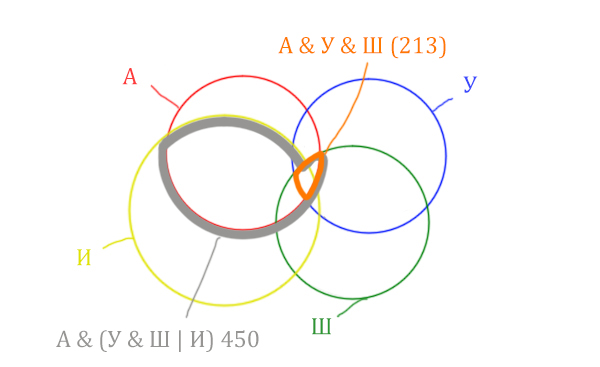
Отметим Англия & Уэльс & Шотландия &
Ирландия – это общая территория четырёх кругов. Область получается ещё
меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх
кругах одновременно. Отмечено фиолетовым цветом.
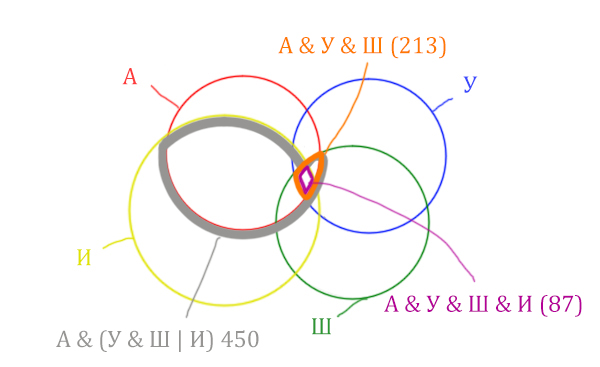
Отметим то, что нужно найти Англия & Ирландия чёрным
цветом.
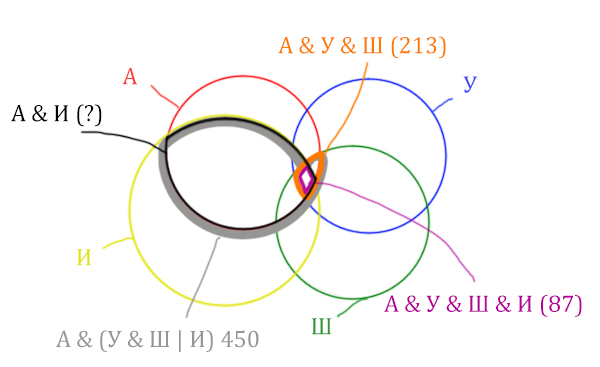
Искомую чёрную область легко найти, если из серой области
вычесть кусочек, окрашенный в бирюзовый цвет!
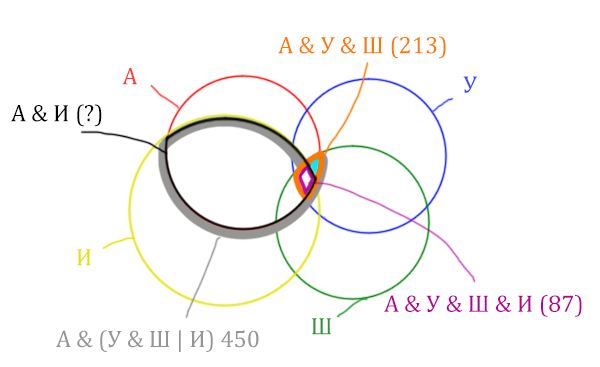
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка)
=
= Англия & Уэльс & Шотландия (213) – Англия
& Уэльс & Шотландия & Ирландия (87) =
= 213 – 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) –
Количество (для бирюзового кусочка) =
450 – 126 = 324
Это и будет ответ!
Ответ: 324.
Разберём задачу из реального экзамена по информатике, которая
была в 2019 году в Москве!
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл
поисковый сервер по этим запросам в некоторым сегменте Интернета:
|
Запрос |
Найдено страниц (в тысячах) |
|
Суфле |
450 |
|
Корзина |
200 |
|
Эклер |
490 |
|
Суфле & Корзина |
70 |
|
Суфле & Эклер |
160 |
|
Корзина & Эклер |
0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова,
поэтому будет три разных круга Эйлера!
Так же видим, что логическое “И” между словами Корзина
и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги
бы не пересекались, если бы операция логического “ИЛИ” совпадала бы с
суммой этих кругов.
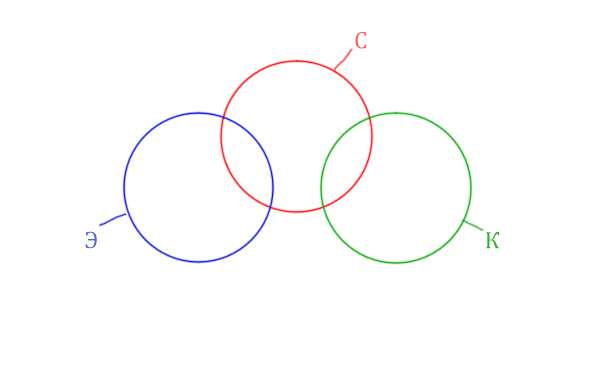
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и
Эклер не пересекаются.
Отметим всё, что нам дано в условии.
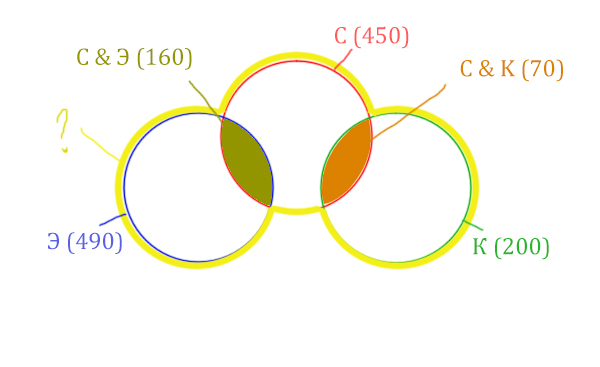
Жёлтым цветом отмечено Суфле | Корзина | Эклер .
Объединение всех трёх кругов. Это то, что нужно найти.
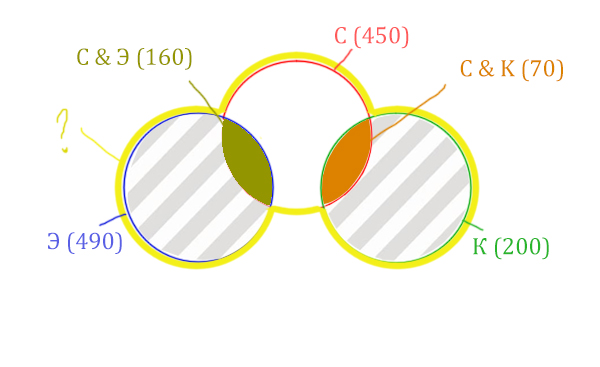
Искомая жёлтая фигура складывается из заштрихованных областей и
красного круга! Площадь красного круга мы знаем. Нужно найти площади
заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область)
=
= Эклер (490) – Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область)
=
= Корзина (200) – Суфле & Корзина (70) =
130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина |
Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область
(130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл
поисковый сервер по этим запросам в некоторым сегменте Интернета:
|
Запрос |
Найдено страниц (в тысячах) |
|
Аврора |
50 |
|
Крейсер |
45 |
|
Заря |
23 |
|
Аврора & Заря |
9 |
|
Заря & Крейсер |
0 |
|
Заря | Крейсер | Аврора |
93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
Количество страниц при запросе Заря & Крейсер равно
нулю. Значит, эти два круга не будут пересекаться.
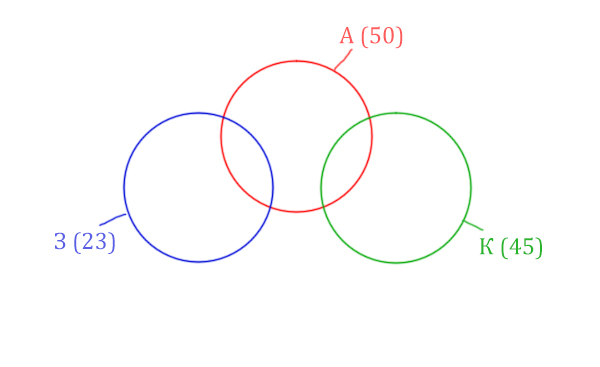
Нарисуем все данные на рисунке.
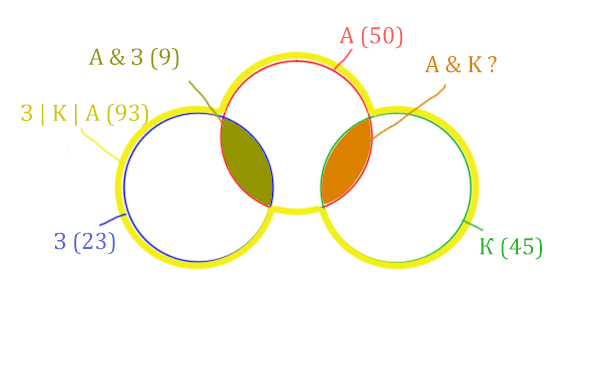
Нужно найти для начала заштрихованную правую часть.
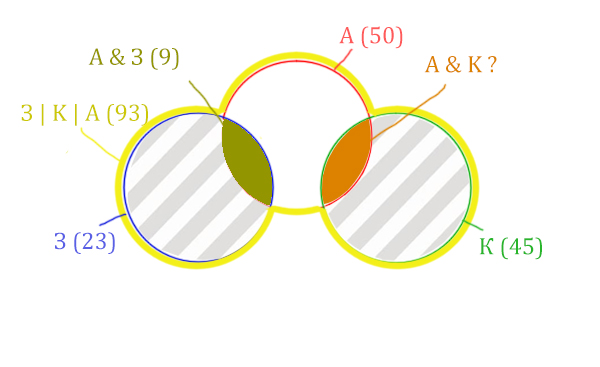
Количество страниц (для двух заштрих.
частей) =
З | К | А (93) – Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих.
части) =
Синий круг (23) – А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части)
=
Колич. страниц (для двух заштрих. частей) (43) – Колич. страниц (для лев.
заштрих. части) (14) =
= 43 – 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) – Колич. страниц (для правой заштрих. части) (29) =
45 – 29 = 16
Ответ: 16
Как зарегистрироваться в ЛК на сайте Море ТВ

Море ТВ — это портал, позволяющий просматривать фильмы и сериалы в любой точке России. За пользование порталом предусмотрена оплата. Однако есть специальные промо-коды, которые могут в разы снизить стоимость подписок. Для использования функционала сайт Море ТВ нужно войти в личный кабинет.
Войти в личный кабинет
Содержание
- 1 Регистрация личного кабинета
- 2 Вход в личный кабинет
- 3 Возможности личного кабинета
- 4 Подключение подписки
Регистрация личного кабинета
Регистрация проводится по такой инструкции:
- Зайти на главную страницу портала по адресу https://more.tv.
- В правом верхнем углу экрана есть кнопка «Войти», на нее нужно нажать.
- В первую очередь, необходимо указать адрес электронной почты и нажать кнопку «Продолжить». На следующей странице система запрашивает пароль, его нужно придумать самостоятельно. На этом регистрация завершается.
- Регистрация означает автоматическое согласие клиента с пользовательским соглашением и политикой конфиденциальности.
Важно! Есть возможность авторизации через одну из наиболее популярных социальных сетей. На выбор пользователя предлагаются Одноклассники, Вконтакте, Гугл, Фейсбук, Apple ID. Если пользователь решит воспользоваться этим способом, ввод данных не потребуется, так как система получает их автоматически.
Войти в личный кабинет
Вход в личный кабинет
Каждый последующий вход в личный кабинет выполняется по такой инструкции:
- Зайти на главную страницу сайта https://more.tv.
- В правом верхнем углу нажать кнопку «Вход».
- Указать данные авторизации — адрес электронной почты и пароль, заданный при регистрации.
- Нажать кнопку «Вход».
При входе через одну из социальных сетей необходимо выбрать ее логотип и нажать на него.
Возможности личного кабинета
Пользователю открываются такие функции в аккаунте:
- Просмотр любого контента в самом высоком качестве без перерывов на рекламные паузы.
- Доступ ко всем телеканалам, которые являются закрытыми на телевизионных приставках.
- Подключение и использование Смарт-ТВ.
- Использование промо-кодов для снижения стоимости подписок.
- Управление просмотром. Эта функция дает возможность пользователю записать интересующий фильм или передачу, также при просмотре можно ставить фильм на паузу, смотреть архивные программы.
- Осуществление поиска по жанрам, году и стране выпуска.

Кроме личного кабинета, используемого на персональном компьютере, пользователи могут скачать мобильное приложение Море ТВ и пользоваться им на планшетах и смартфонах. Также это приложение действует и на телевизорах, обладающих функцией Смарт-ТВ.
Важно! Скачать приложение можно официального маркета — Google Play или App Store.

Незарегистрированный пользователь имеет ограниченный набор действий на портале. Доступно изучение описаний фильмов и актерского состава в них, а также рецензий. Зарегистрированному пользователю открываются безграничные возможности Море ТВ:
- Просмотр новейших телесериалов отечественного и зарубежного производства, а также прочих новинок, которые еще не выставлялись в эфир.
- Просмотр эксклюзивного контента more originals, выпускаемый порталом.
- Посещение частных коммерческих телеканалов.
- Отсутствие рекламных роликов и баннеров при просмотре любого канала.
- Просмотр игр ММА и турниров UFC в режиме онлайн.
Подключение подписки
Подключение выполняется по такой инструкции:
- Право на подключение платных подписок получают зарегистрированные пользователи.
- В первую очередь, нужно зайти на главную страницу сайта Море ТВ и найти активное окно «Оформить подписку».
- Система перенаправляет пользователя на следующую страницу, где нужно снова нажать кнопку «Оформить».
- После этого открывается отдельная страница с небольшой анкетой. В ней нужно последовательно указать адрес электронной почты или выбрать одну из предложенных социальных сетей.
- В первом случае на указанный адрес электронной почты приходит письмо с активной ссылкой, прохождение по которой подтверждает намерение подписаться.
- В завершение следует выбрать способ оплаты и произвести ее.

Несмотря на то, что подписка обычно платная, можно использовать тестовый вариант на 7 или 14 дней. Иногда можно получить акционные предложения на скидку в размере 100%.
Для того чтобы получить хорошие скидки, используются промо-коды. Их можно получить на некоторых веб-сайтах и в социальных сетях, эти сервисы раздают коды посетителям с согласия владельцев кинотеатра Море ТВ.
Подписку при желании можно отключить. Для этого нужно войти в раздел «Управление подпиской» в личном кабинете. До тех пор, пока подписка не будет отключена, деньги будут сниматься с карты. Так как подписка оформляется на определенный срок, отключить ее можно только по истечении этого периода. До конца срока подписка считается оплаченной и отключению не подлежит.
The following two tabs change content below.
- Биография
- Последние записи

В 2011 году окончил ФГОБУ ВО «Финансовый университет при Правительстве Российской Федерации» по специальности «Экономист». В настоящее время помогаю в освоении сайта cabinet-bank.ru, и готов ответить на Ваши вопросы. (Страница автора)

Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер – швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
Задача (Простая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу “Пушкин” в поисковике нашлось 3500 страниц. По запросу “Лермонтов” – 2000 страниц.
Запрос “Пушкин | Лермонтов” обозначает, что поисковик выдаст страницы, где есть слова про “Пушкина”, и страницы, где есть слова про “Лермонтова”, а так же могут быть страницы, где написано и про “Пушкина”, и про “Лермонтова” одновременно.
Если сложить страницы, в которых написано про “Пушкина” и про “Лермонтова” получается 3500 + 2000 = 5500 страниц. Но почему же при запросе “Пушкин | Лермонтов” получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про “Пушкина” (3500 страниц), мы подсчитали и те страницы, где было написано и про “Пушкина”, и про “Лермонтова” одновременно.
Тоже самое и для количества страниц, где написано про “Лермонтова” (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про “Пушкина”, и про “Лермонтова”.
В вопросе спрашивается, сколько страниц будет по запросу “Пушкин & Лермонтов“. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про “Пушкина”, и про “Лермонтова”.
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) – 4500 = 5500 – 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: “Пушкин” и “Лермонтов”. Поэтому рисуем два пересекающихся круга, желательно разными цветами.
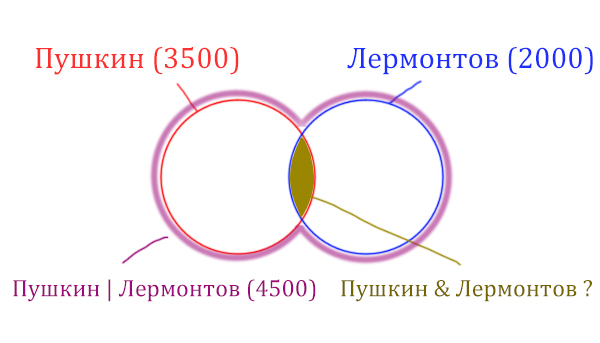
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию “Пушкин | Лермонтов”. Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» “Пушкин | Лермонтов” (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
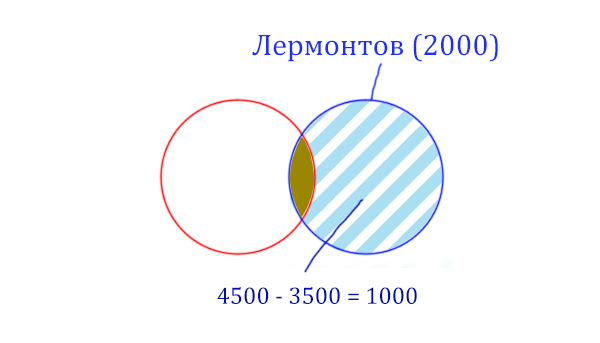
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 – 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
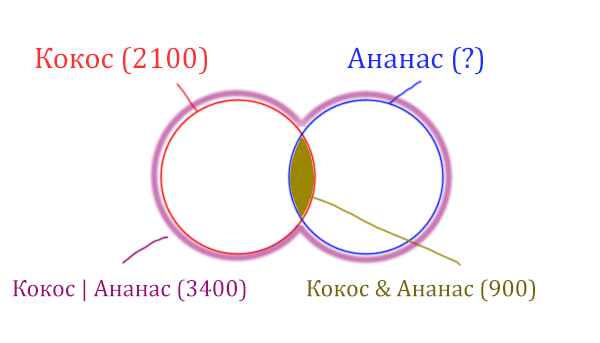
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 – 900 = 1200.
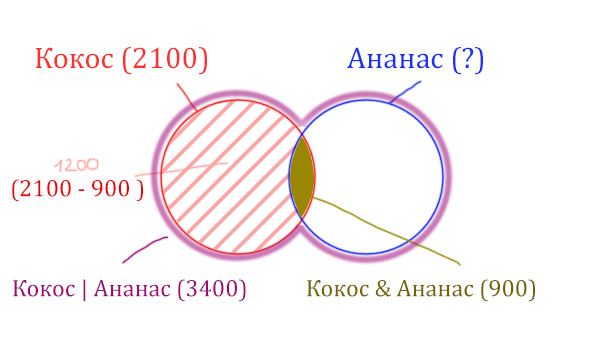
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 – 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического “ИЛИ”.
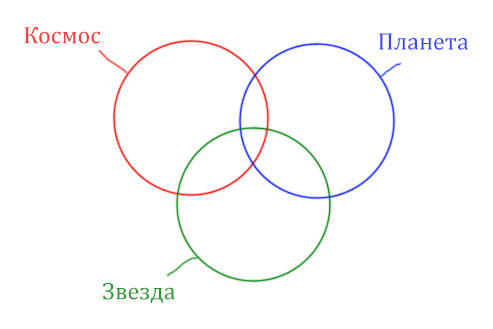
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
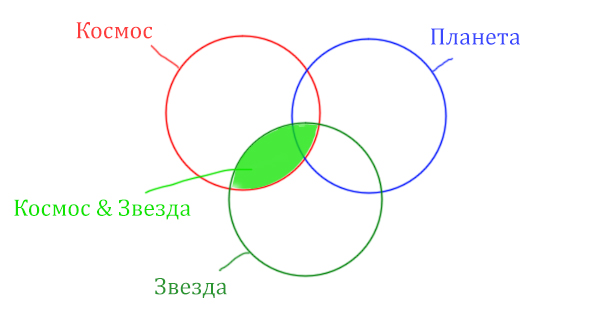
Теперь отметим вторую скобку Космос & Планета.
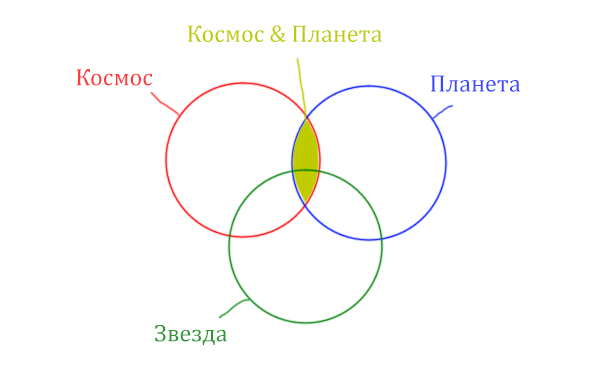
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического “ИЛИ”. Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
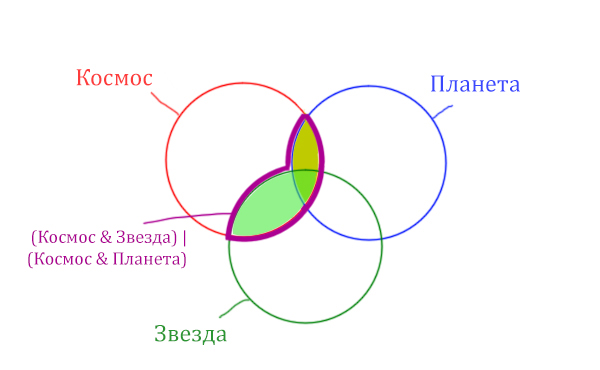
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
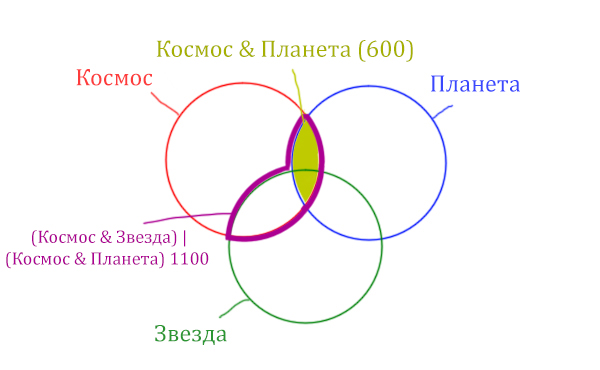
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
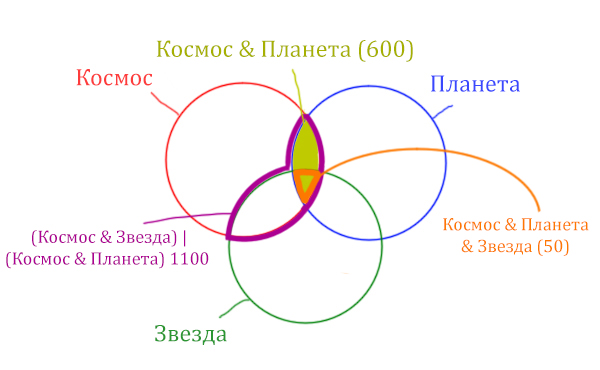
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
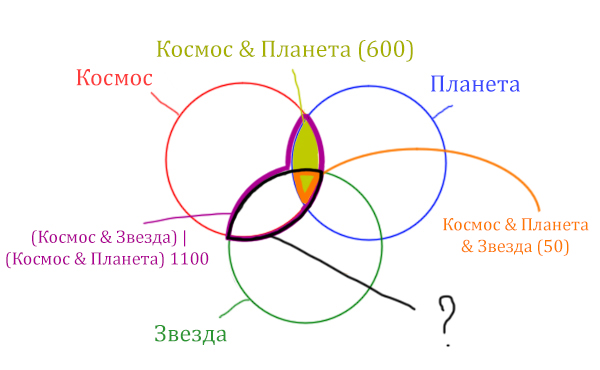
Теперь у нас есть все компоненты, чтобы решить эту задачу.
Найдём заштрихованную область.
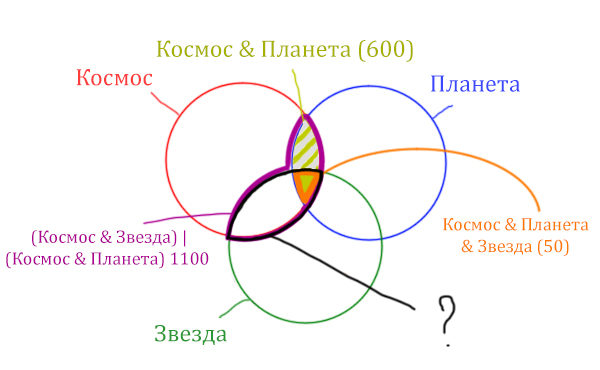
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 – 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 – 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
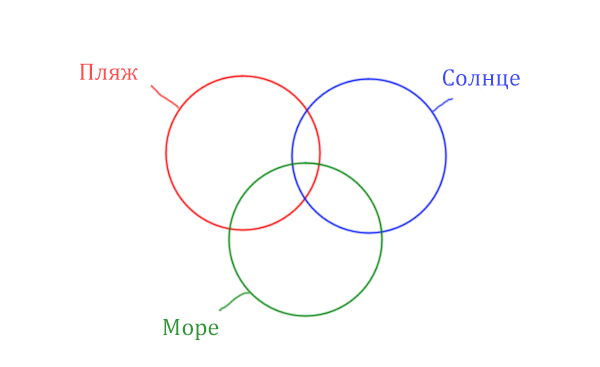
Отметим все области для которых нам даны количество страниц.
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
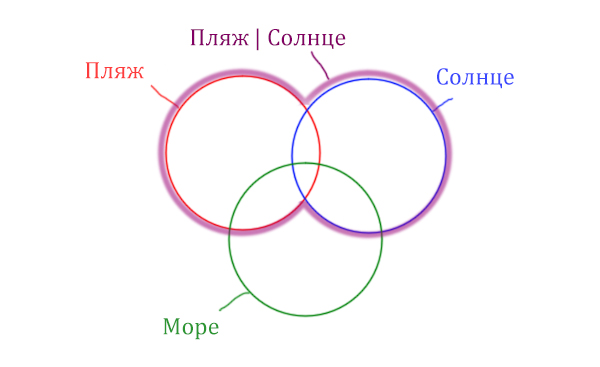
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
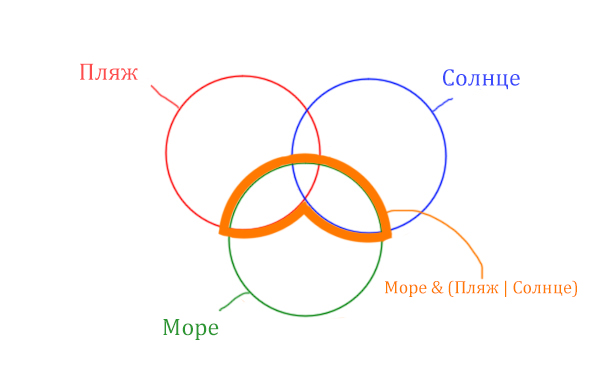
Теперь отметим Море & Пляж.
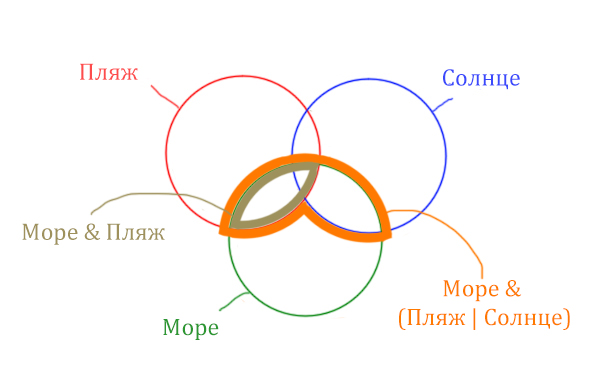
Теперь отметим Море & Солнце.
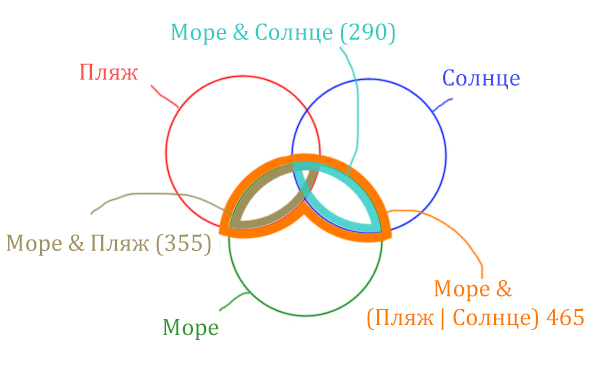
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
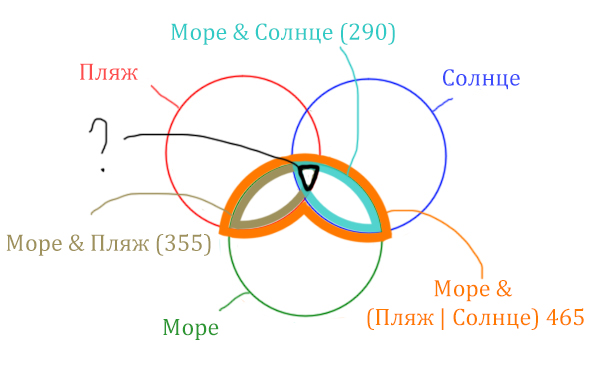
Найдём заштрихованную область!
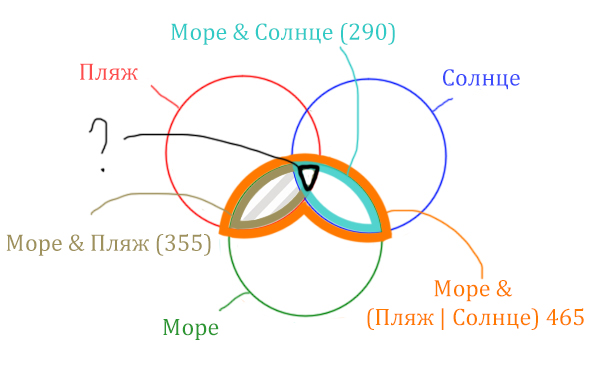
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) – Море & Солнце =
= 465 – 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) – Количество страниц (в заштрихованной области) 175 =
= 355 – 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
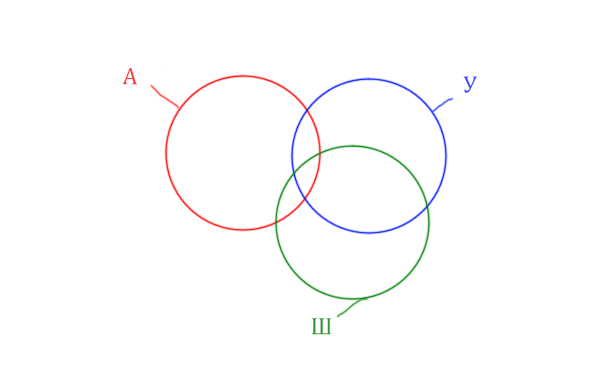
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
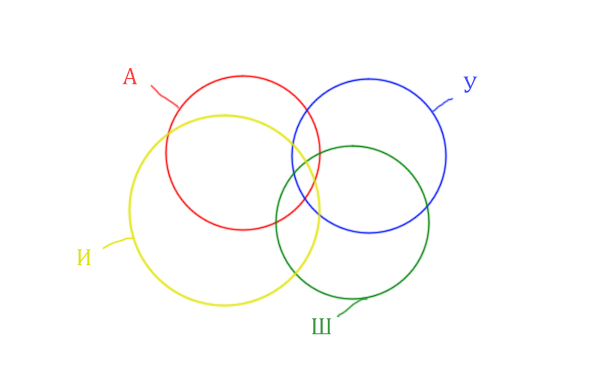
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
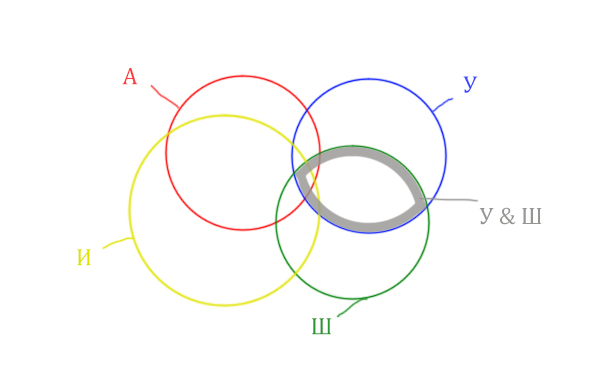
Добавим к этой области Ирландию через логическое “ИЛИ”. Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
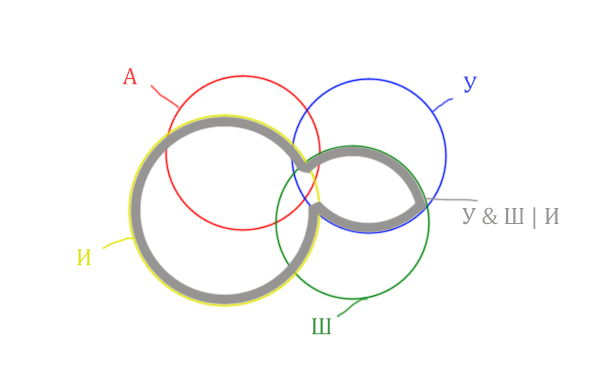
Теперь нужно сделать операцию логического “И” получившийся области с “Англией”. Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
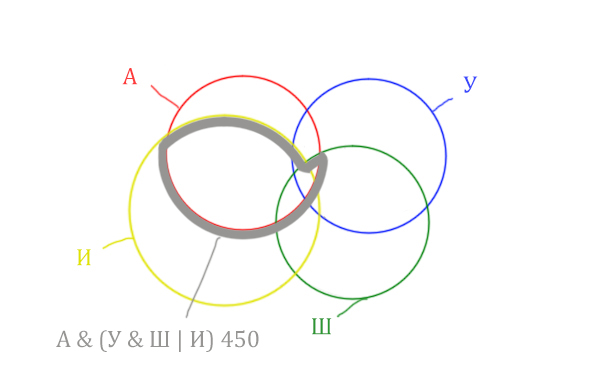
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия – это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
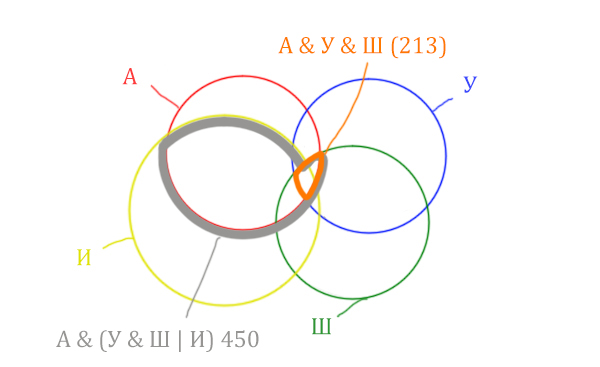
Отметим Англия & Уэльс & Шотландия & Ирландия – это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
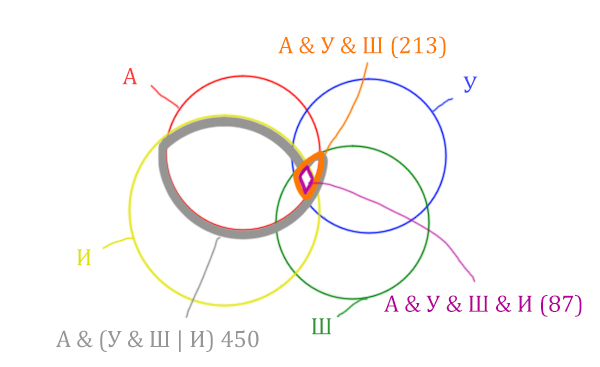
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
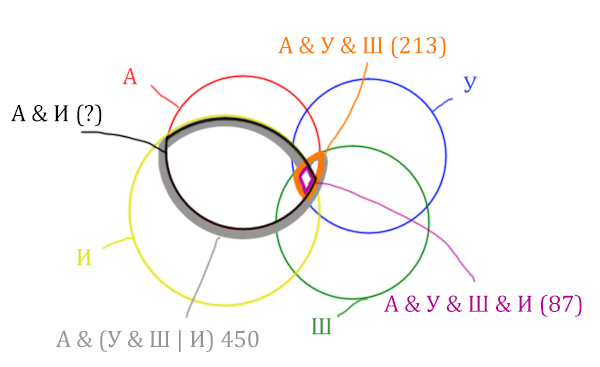
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
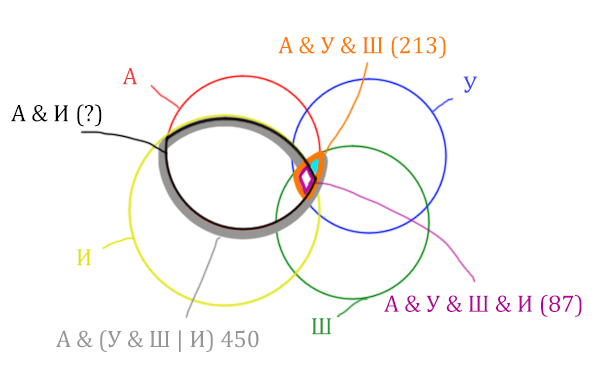
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) – Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 – 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) – Количество (для бирюзового кусочка) =
450 – 126 = 324
Это и будет ответ!
Ответ: 324.
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое “И” между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического “ИЛИ” совпадала бы с суммой этих кругов.
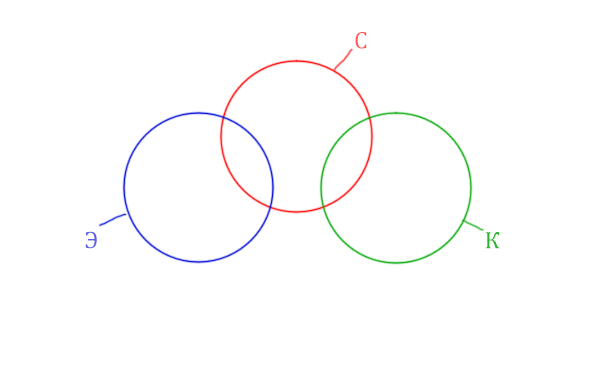
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
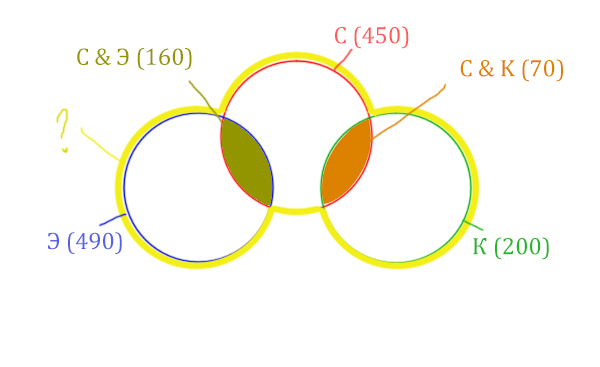
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
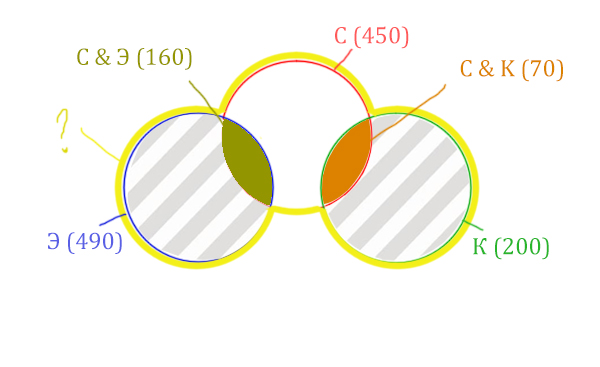
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) – Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) – Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
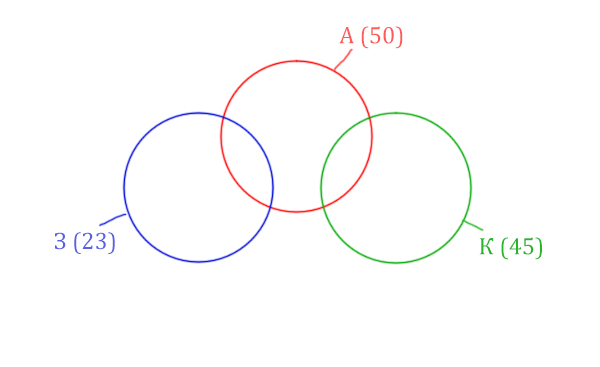
Нарисуем все данные на рисунке.
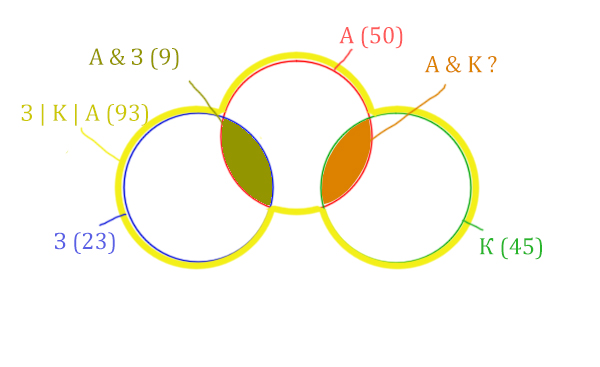
Нужно найти для начала заштрихованную правую часть.
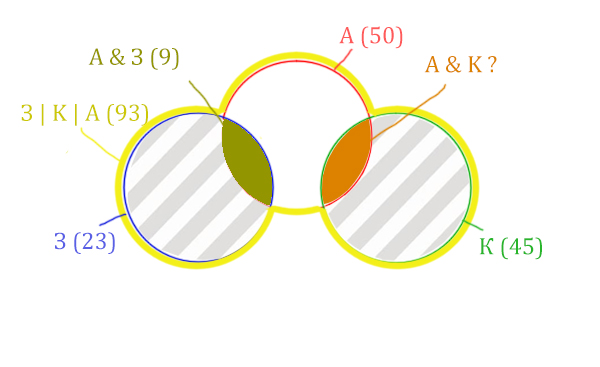
Количество страниц (для двух заштрих. частей) =
З | К | А (93) – Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) – А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) – Колич. страниц (для лев. заштрих. части) (14) =
= 43 – 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) – Колич. страниц (для правой заштрих. части) (29) =
45 – 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Интересно…
как быть , когда идет произведение3 предметов + произведниее 3 педметов..
ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++
В операционной систем Линукс для просмотра больших текстовых файлов используется команда more. В отличии от less, она позволяет читать файлы по одной странице.
Это очень полезная функция, так как часто бывает, что не удается прочитать очень большие текстовые документы и это касается не только Linux ну и Windows. Обычно это происходит с логами. К примеру копится годами какой-нибудь лог и занимает где-то 30 гигабайт. Возникла потребность открыть его и посмотреть, что происходит.
Стандартные утилиты не смогут этого сделать, а если им это удастся, вывод читать будет крайне неудобно, так как очень много текста. В этой ситуации можно воспользоваться утилитой more.
Содержание
- 1 Синтаксис
- 1.1 Примеры
Синтаксис
Рассмотрим синтаксис команды.
more опции файлы
Основные опции:
- -d – показывает в конце страницы подсказки, например “Нажмите пробел для продолжения”.
- -f – считает логические строки.
- -с – текст показывается сверху, при этом стирает предыдущий вывод.
- -p – очистка терминала, как и параметр “-с”. Используется для того, чтобы не было прокрутки и информацию было удобно читать.
- -s – заменяет пустые строки, которые стоят рядом на одну.
- -u – убирает подчеркивание.
- –help – вывести справочную информацию.
- -v – текущая версия утилиты.
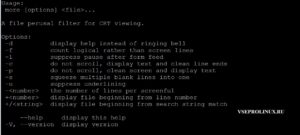
После запуска утилиты, управление осуществляется горячими клавишами.
Чтобы осуществить переход на другую страницу используется клавиша “Пробел”. Для смещения на одну строчку вниз – “Enter”.
Основные горячие клавиши:
- h – мини help. Выдаст описание команд.
- :f – утилита покажет имя текущего файла и количество строк.
- z или “Пробел” – переход на следующую страницу.
- = – выводит количество строк на данный момент.
- q – выход из more.
Примеры
Для первого примера запустим утилиты без параметров, а именно прочитаем лог “daemon.log”, который состоит из двух страниц.
more daemon.log
 Итак, это была только первая страница. Перейдем на вторую, нажав клавишу “Пробел”.
Итак, это была только первая страница. Перейдем на вторую, нажав клавишу “Пробел”.
Утилита more позволяет читать несколько файлов. В этом случае нужно вводить имена документов по очереди, разделяя их пробелом. Вывод текста будет осуществляться в таком же порядке.
Прочитаем два лога. Один auth.log, второй – daemon.log.
more auth.log daemon.log
Как видно из скриншота, первый лог оказался небольшим. Чтобы перейти во второй документ нажмем “Пробел”.
Откроем документ, которые лежит в домашнем каталоге /home/ya/dokument.
more /home/ya/dokument

Как видно из скриншота выше, в документе много пустых строк, чтобы убрать повторы, введем команду с опцией “-s”.
more -s /home/ya/dokument

Круги Эйлера в информатике
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.
Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.
Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.
Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».
В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».
Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.
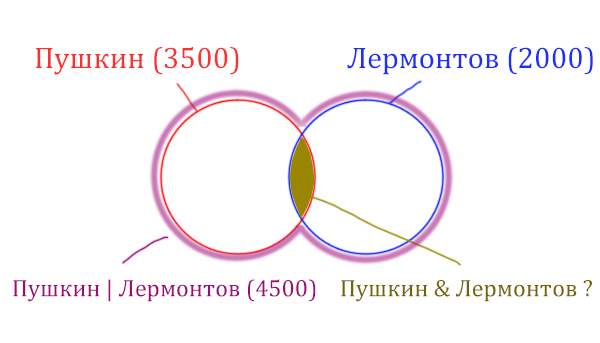
Объединение двух кругов в общую фигуру ( показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
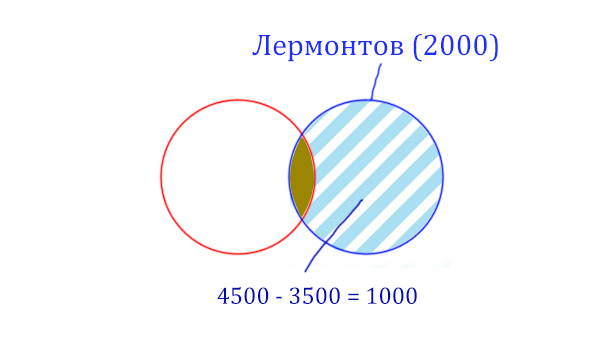
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Рассмотрим ещё одну не сложную разминочную задачу.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
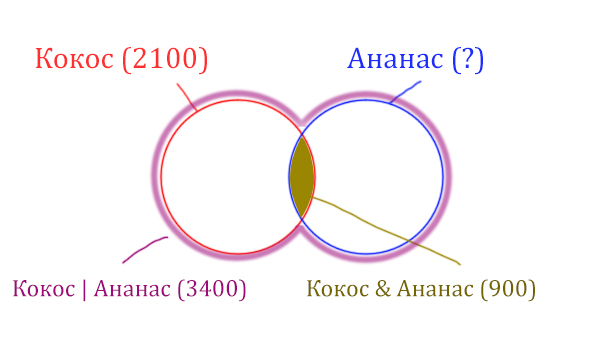
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.
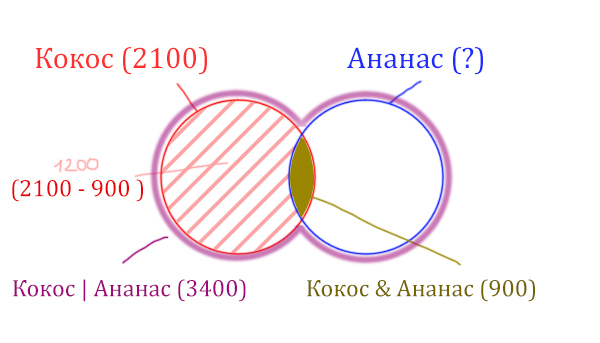
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».
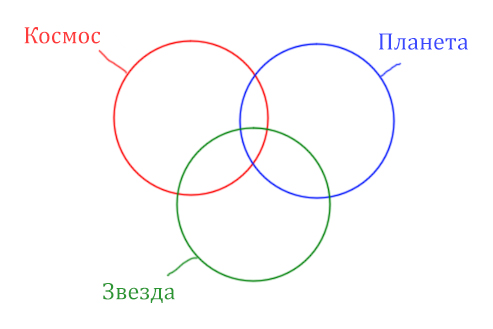
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
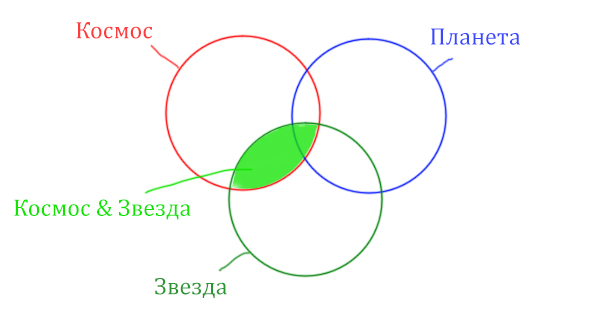
Теперь отметим вторую скобку Космос & Планета.
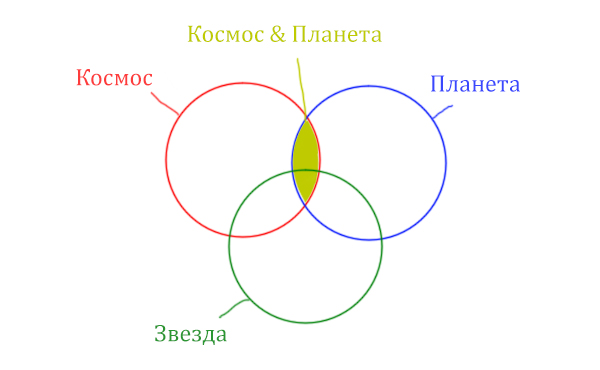
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
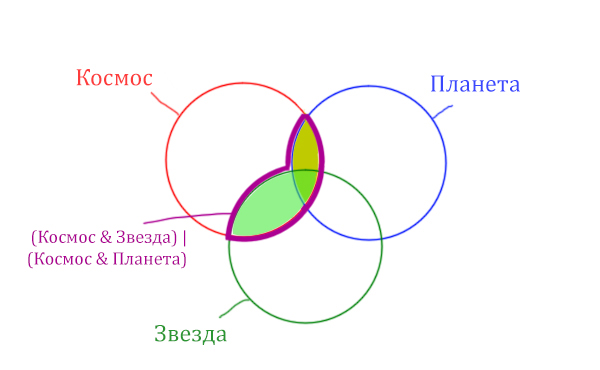
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
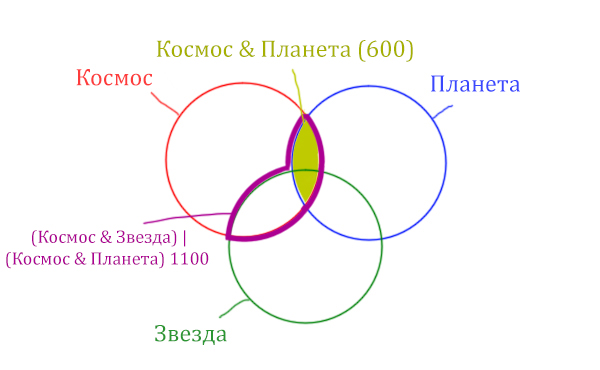
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
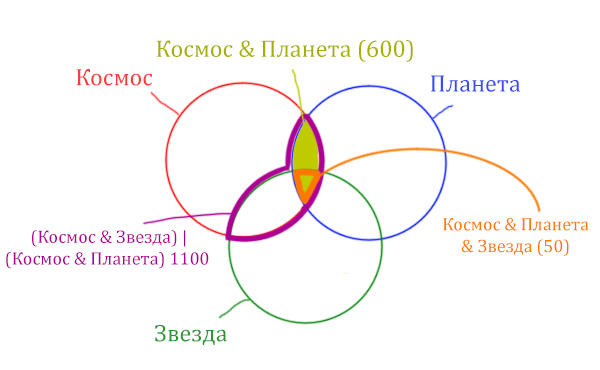
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
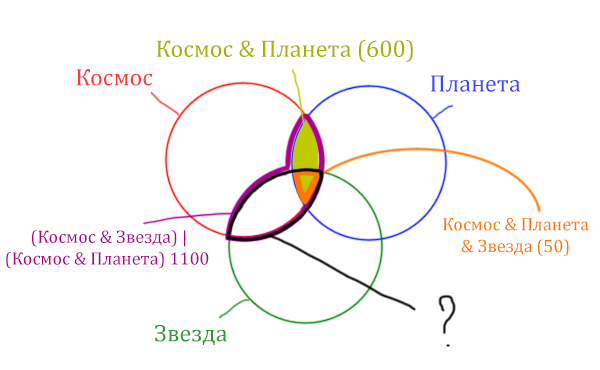
Теперь у нас есть все компоненты, чтобы решить эту задачу.
Найдём заштрихованную область.
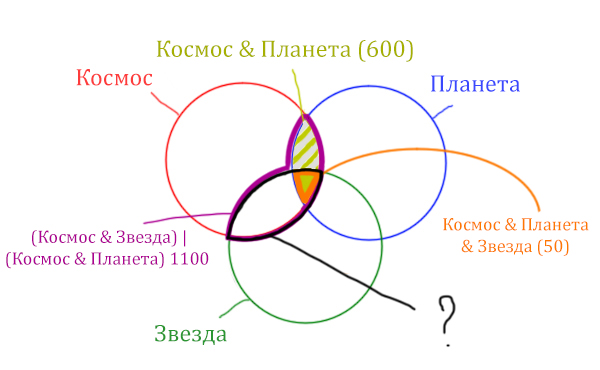
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 — 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
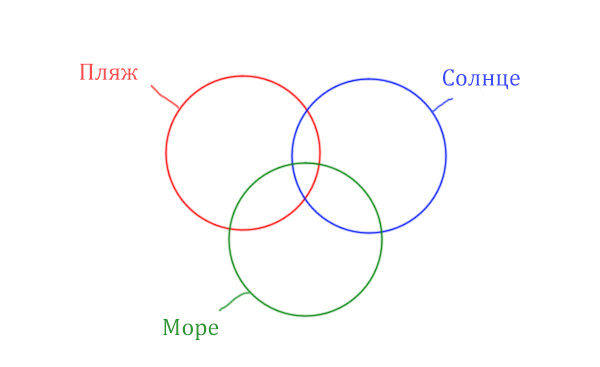
Отметим все области для которых нам даны количество страниц.
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце) 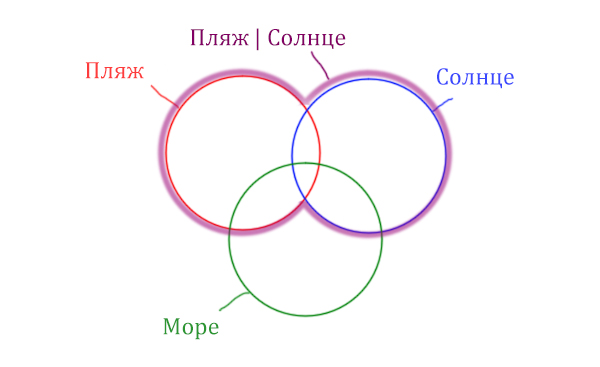
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
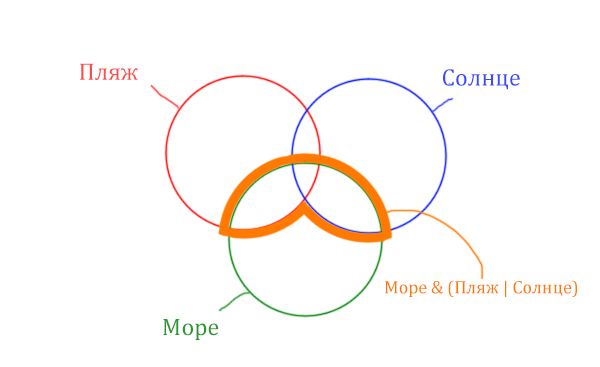
Теперь отметим Море & Пляж.
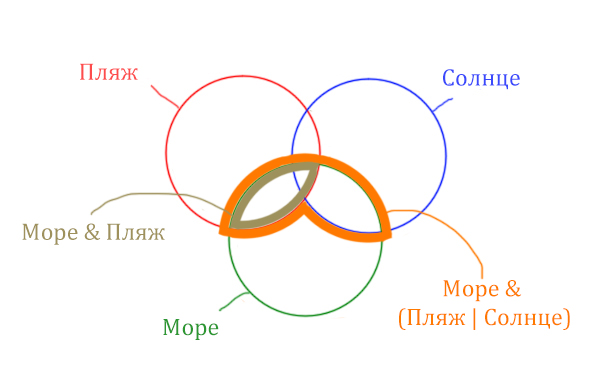
Теперь отметим Море & Солнце.
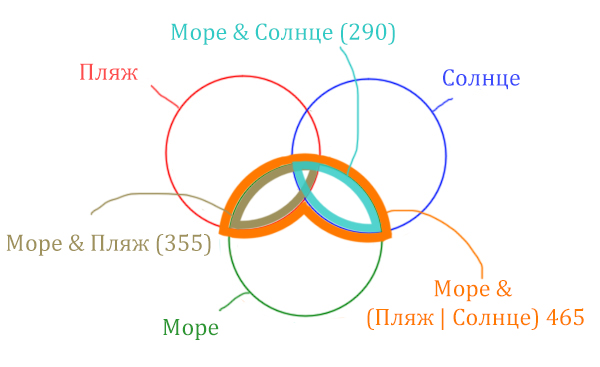
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
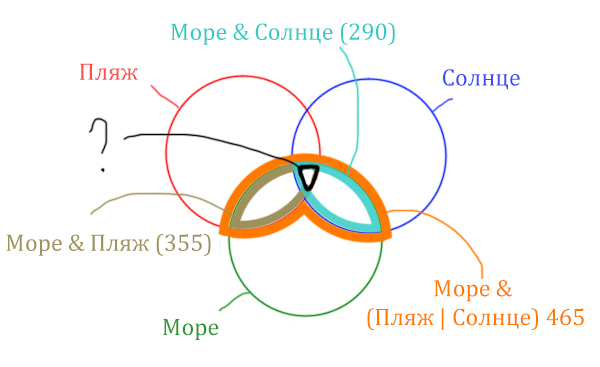
Найдём заштрихованную область!
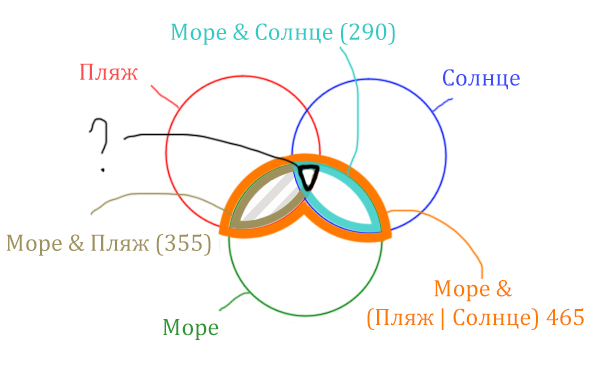
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
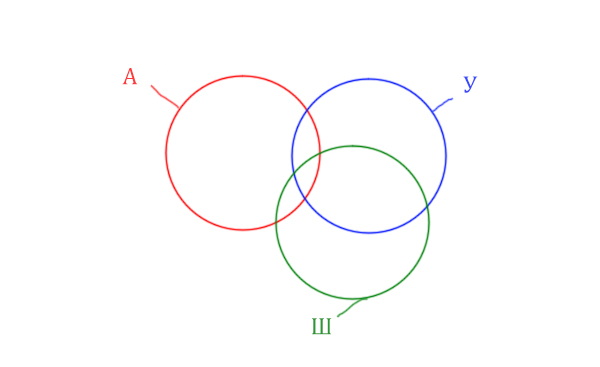
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
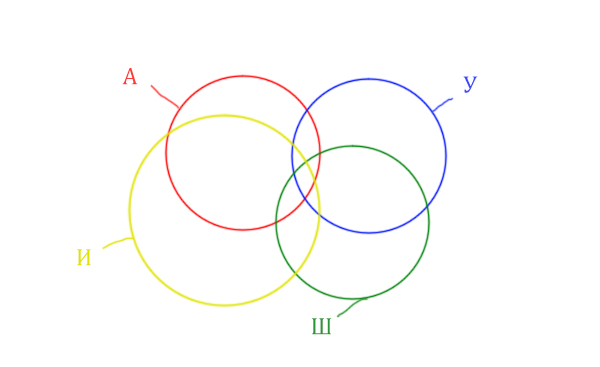
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
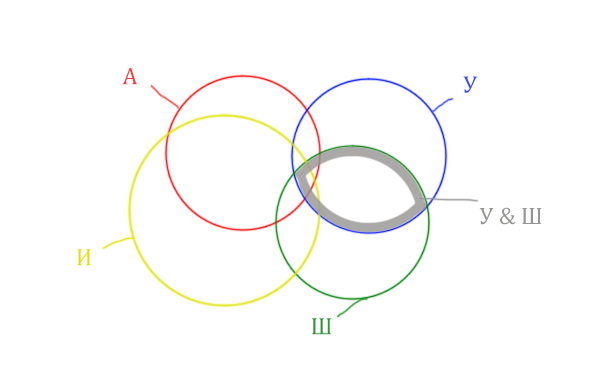
Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
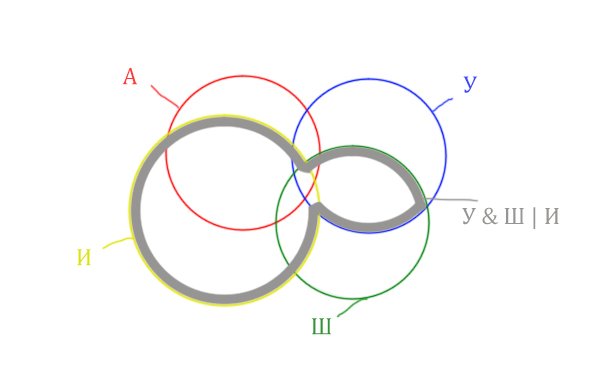
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
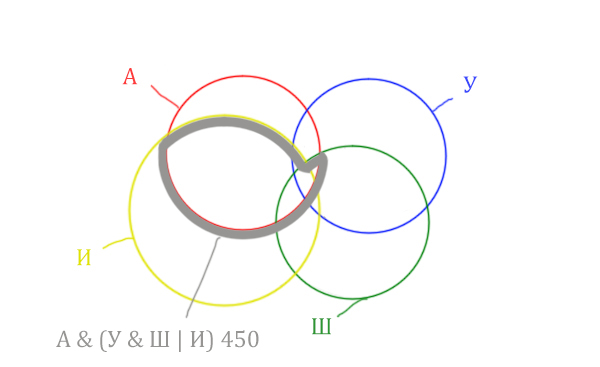
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
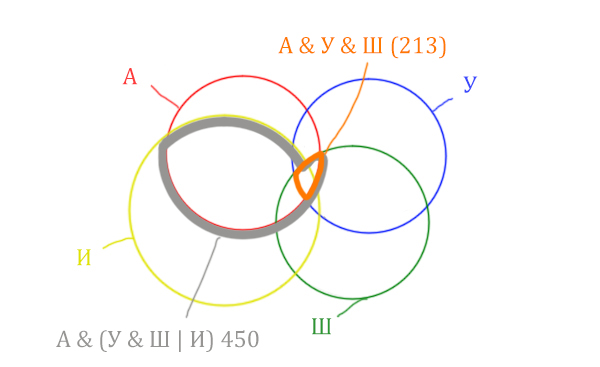
Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
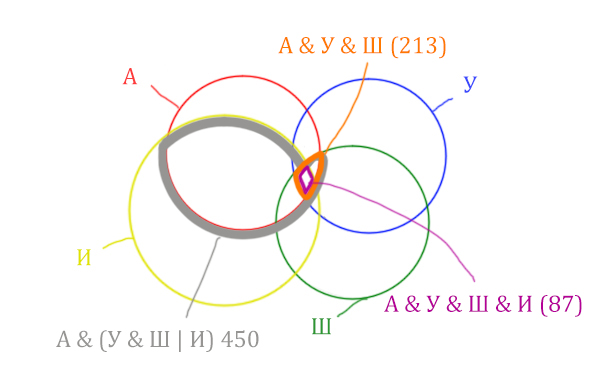
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
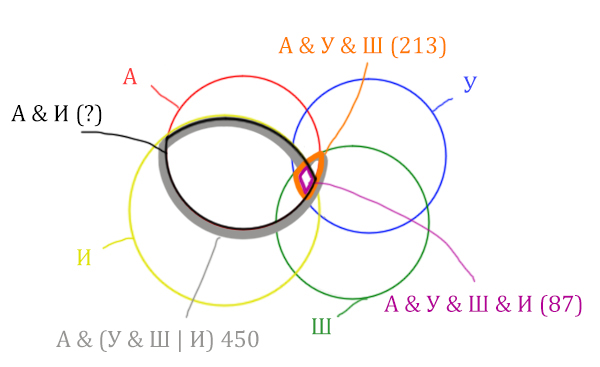
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
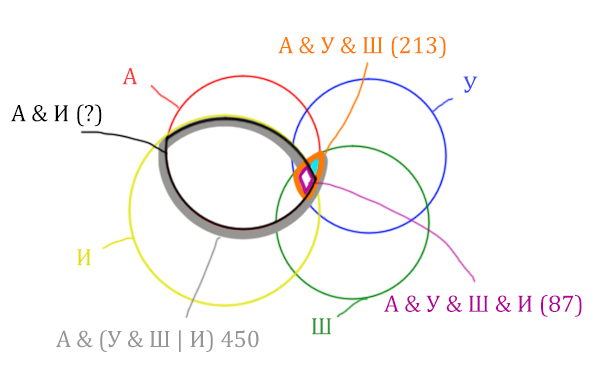
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324
Это и будет ответ!
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.
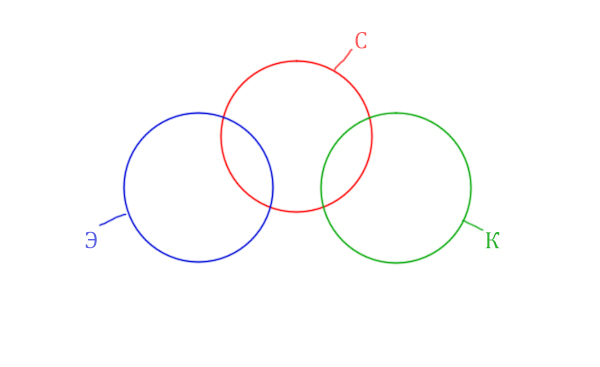
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
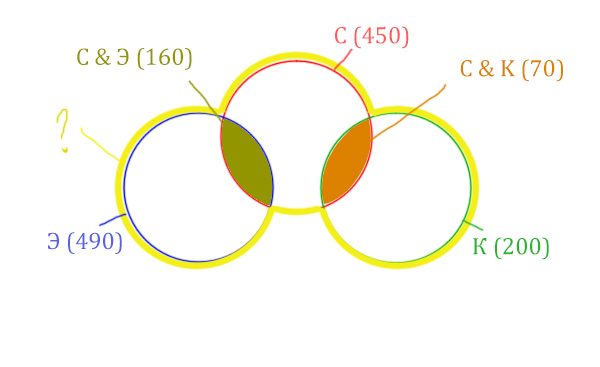
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
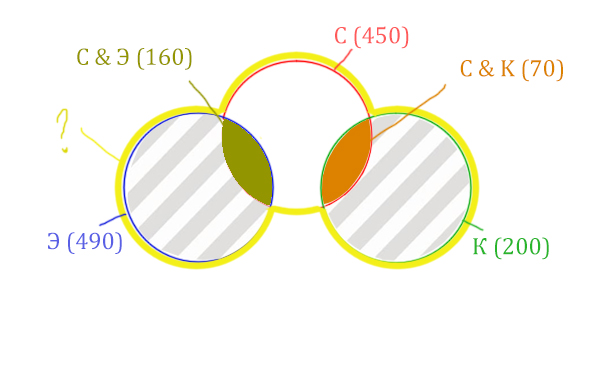
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
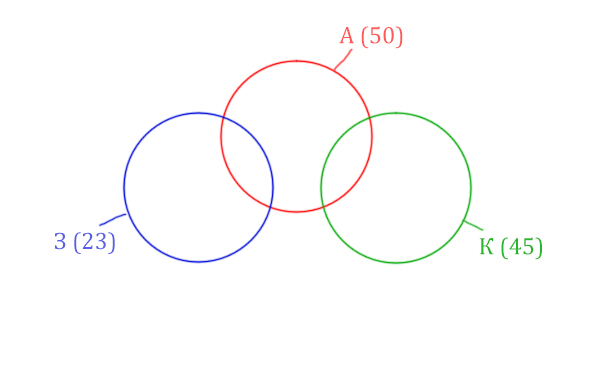
Нарисуем все данные на рисунке.
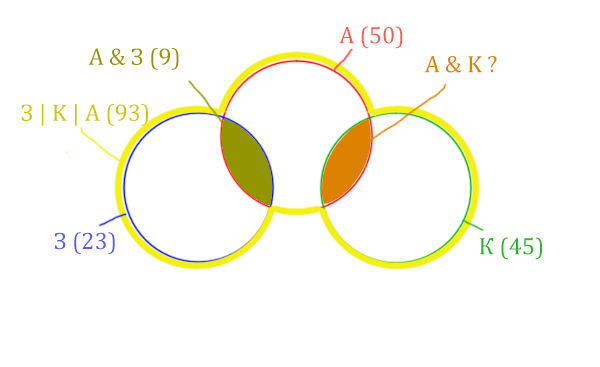
Нужно найти для начала заштрихованную правую часть.
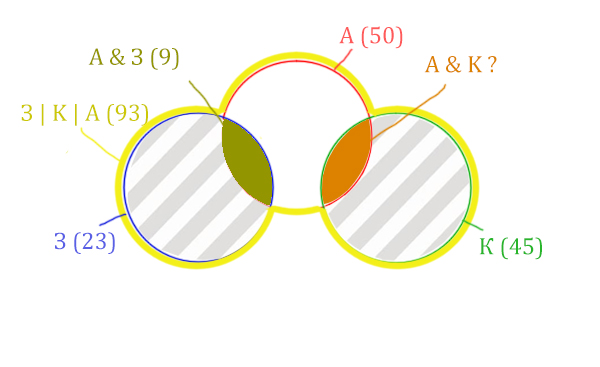
Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Источник

