Субдифференциал функции f, заданной на банаховом пространстве E — это один из способов обобщить понятие производной на произвольные функции. Хотя при его использовании приходится пожертвовать однозначностью отображения (значения субдифференциала в общем случае — множества, а не отдельные точки), он оказывается довольно удобным: любая выпуклая функция оказывается субдифференцируемой на всей области определения. В тех случаях, когда о дифференцируемости функции заранее ничего не известно, это оказывается существенным преимуществом.
Кроме того, субдифференциал (при довольно слабых ограничениях на функцию) по своим свойствам во многом подобен обычной производной. В частности, для дифференцируемой функции они совпадают, а для недифференцируемой он оказывается как бы «множеством возможных производных» в данной точке. Значения субдифференциала являются выпуклыми подмножествами сопряженного пространства E*.
Определение[править | править код]
Субдифференциалом 




.
Функция 


Вектор 



Свойства[править | править код]
Пусть f1(x), f2(x) — выпуклые конечные функции, причем одна из них непрерывна в точке x, 
, сумма понимается в смысле суммы Минковского.
- Функция имеет локальный минимум в точке тогда и только тогда, когда 0 принадлежит субдифференциалу в этой точке.
Субдифференциал функции на одномерном интервале[править | править код]
Пример[править | править код]
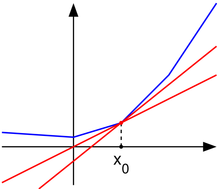
Выпуклая функция (синяя) и “подкасательные” к её графику в точке 
Пусть 





Определение[править | править код]
Субпроизводная выпуклой функции 



для всех 

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


Множество ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)








Примечания[править | править код]
Ссылки[править | править код]
- Половинкин Е. С, Балашов М. В. Элементы выпуклого и сильно выпуклого анализа. — М.: Физматлит, 2004. — 416 с — ISBN 5-9221-0499-3.
- Jean-Baptiste Hiriart-Urruty, Claude Lemaréchal Fundamentals of Convex Analysis. — Springer, 2001. ISBN 3-540-42205-6.
Выпуклые функции в общем случае могут
быть недифференцируемы в обычном смысле
(например, f(x)
= |x| недифференцируема в
точке х = 0).
Определение. Производной по
направлению p(p
Rn,
p
0)
функции f в точке х
называется
![]()
![]()
и обозначается f ’(x,
p) или
![]()
(х).
Отметим, что если f(x)
дифференцируема в точке х, то f
’(x, p) = (f
’(x),p), где
f ’(x) =
– градиент функции f в
точке х.
Теорема Радемахера. Всякая
выпуклая функция является дифференцируемой
почти всюду (за исключением множества
лебеговой меры нуль) на открытом множестве
Х
dom
f.
Теорема. Пусть f(x)
– выпуклая функция на Rn.
Тогда для любой точки х
int(dom
f) существует и конечна
производная функции f по
любому направлению pRn.
Для выпуклых функций можно определить
понятие субградиента, которое заменяет
обычное понятие градиента гладкой
функции в задачах на экстремум.
Определение. Вектор g
называется субградиентом функции
f в точке х0
dom
f, если
f(x) –
f(x0)
(g,
x – x0)
для любых х
Rn.
Множество всех субградиентов функции
f в точке х0 называется
субдифференциалом функции f
и обозначается
f(x0).
Замечание. В определении
субградиента не требуется выпуклости
функции и можно вычислить субградиент
в заданной точке и для произвольной
функции. Однако для выпуклой функции,
определённой на открытом выпуклом
множестве, всегда существует хотя
бы один субградиент в любой точке
множества, т.е. её субдифференциал
является непустым множеством. Для
произвольной функции это не так.
Геометрический смысл понятия
субдифференциала
Можно показать, что если f(x)
выпуклая функция, то
1) вектор g![]()
f(x0)
является внешней нормалью
опорной гипреплоскости к множеству
уравня M(f)
функции f в точке х0,
где M(f) =
{x
Rn|
f(x)
f(x0)};
2) вектор (g, – 1)Rn+1,
где g
f(x0),
является внешней нормалью
опорной гиперплоскости, проведённой к
надграфику функции f в
точке (x0, f(x0))
(в частности, если x
R,
то g есть тангенс угла
наклона опорной прямой, проведённой к
надграфику функции f);
3) для функции f: R
R
f(x)
= [f ’(x –
0), f ’(x +
0)].
Свойства
субдифференциала выпуклой функции
Пусть f(x) –
выпуклая функция, определённая на
открытом выпуклом множестве Х
dom
f. Тогда справедливы
следующие утверждения.
1. Субдифференциал
f(x0)
– непустое выпуклое, замкнутое и
ограниченное множество для любой точки
х0
Х.
2. Если f(x)
– дифференцируемая функция в точке
х0
Х,
то
f(x0)
= {f ’(x0)}.
3. Пусть h(x)
= αf(x), α >
0, тогда
h(x)
= αf(x) для
x
X
4. Пусть f(x)
= f1(x)
+ f2(x),
где f1(x)
и f2(x)
– выпуклые на Х функции, тогда
f(x)
=
f1(x)
+
f2(x)
для
х
Х.
5. Пусть функции f1,
f2, … ,fm
– выпуклые функции, определённые на Х,
и f(x) =
![]()
fi(x).
Тогда
f(x)
= conv![]()
для
х
Х,
где I(x) = {i =
:
fi(x)
= f(x)}.
6.Производная функции f в
произвольной точке по любому направлению
p
Rn,
p
0
существует и
f ’(x, p)
=
![]()
(g, p).
Замечание. Требование открытости
множества Х существенно. Если Х
– произвольное выпуклое множество, то
в его граничных точках свойства 1 – 6
будут выполняться только при некоторых
дополнительных предположениях.
В общем случае вычисление субдифференциала
f(x)
задача непростая. Один из инструментов
решения этой задачи даёт теорема Кларка.
Теорема Кларка. Пусть x0
int
dom f, f(x)
– выпуклая функция на Rn,
Q – множество точек
пространства Rn,
в которых функция f(x)
недифференцируема, {xk}
– произвольная последовательность,
сходящаяся к x0(xk
Q
для любого k), такая, что
последовательность
![]()
сходится. Тогда субдифференциал функции
f(x) в точке
x0 совпадает с
выпуклой комбинацией всех пределов
последовательностей
![]()
для всевозможных последовательностей
{xk},
т.е.
f(x0)
= Conv
.
Примеры
1. Пусть f(x)
= |x|. Требуется вычислить
f(x).
Если х > 0, то f(x)
= x, f ’(x)
= 1, следовательно,
f(x)
= Conv{1} = {1}. Аналогично для
x < 0
f(x)
= Conv{-1} = {-1}. Пусть х = 0.
Заметим, что это единственная точка, в
которой функция f(x)
недифференцируема. Тогда

= {-1, +1},
f(0)
= Conv{-1, +1} = [-1, 1].
2. Пусть f(x1,
x2) = |x1|
+ |x2|. Требуется
вычислить
f(x).
З
аметим,
что f(x1,
x2) =
Функция f(x1,
x2) дифференцируема
в любой точке пространства, кроме точек,
для которых выполнено одно из условий:
|x1| = 0 или |x2|
= 0, т.е. Q = {x
R2:
x1 = 0}![]()
{x
R2:
x2 = 0}.
Пусть x
Q,
тогда f ’(x1,
x2) =
![]()
,
если x1 > 0, x2
> 0;
f
’(x1, x2)
=
![]()
,
если x1 > 0, x2
< 0;
f ’(x1,
x2) =
![]()
,
если x1 < 0, x2
> 0;
f ’(x1,
x2) =
![]()
,
если x1 < 0, x2
< 0.
На Рис. 13 представлены области, в которых
функция дифференцируема и значения
градиентов одинаковы.

Для точек
х0
Q
субдифференциал состоит из единственного
элемента, совпадающего с градиентом
функции в этой точке.
Пусть х0
Q,
причём х0 лежит на оси Ох1 и
х10 > 0. Тогда

=![]()
поэтому
![]()
Аналогично вычисляется субдифференциал
для других точек множества Q.
Таким образом,
![]()
Заметим, что некоторые свойства
субдифференциалов, приведённые выше,
легко получить как следствие из теоремы
Кларка.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Методы Оптимизации. Даниил Меркулов. Субградиент. Субдифференциал.
Directional derivative
Производная по направлению
Пусть $f(x)$ – выпуклая функция на выпуклом множестве $S subseteq mathbb{R}^n$ и пусть $x_0 in mathbf{ri} S$. Тогда в $x_0$ существует производная по любому направлению $s in mathbf{Lin} S$:
$$
f'(x_0; s) = lim_{alpha to 0+} dfrac{f(x_0 + alpha s) – f(x_0)}{alpha}
$$
Важные факты о производной по направлению
- Если функция $f(x)$ дифференцируема в точке $x_0$, то ее производная по любому направлению $s in mathbb{R}^n$ существует и равна:
$$
f'(x_0; s) = langle nabla f(x_0), srangle
$$
Subgradient
Мотивация
Важным свойством непрерывной выпуклой функции $f(x)$ является то, что в выбранной точке $x_0$ для всех $x in text{dom } f$ выполнено неравенство:
$$
f(x) geq f(x_0) + langle g, x – x_0 rangle
$$
для некоторого вектора $g$, то есть касательная к графику функции является глобальной оценкой снизу для функции.

- Если $f(x)$ – дифференцируема, то $g = nabla f(x_0)$
- Не все непрерывные выпуклые функции дифференцируемы 🙂
Не хочется лишаться такого вкусного свойства.
Субградиент
Вектор $g$ называется субградиентом функции $f(x): S to mathbb{R}$ в точке $x_0$, если $forall x in S$:
$$
f(x) geq f(x_0) + langle g, x – x_0 rangle
$$
Субдифференциал
Множество всех субградиентов функции $f(x)$ в точке $x_0$ называется субдифференциалом $f$ в $x_0$ и обозначается $partial f(x_0)$.
- Если $x_0 in mathbf{ri } S$, то $partial f(x_0)$ выпуклое компактное множество.
- Выпуклая функция $f(x)$ дифференцируема в точке $x_0iff partial f(x_0) = nabla f(x_0)$
- Если $partial f(x_0) neq emptyset ;;; forall x_0 in S$, то $f(x)$ – выпукла на $S$.

Теорема Моро – Рокафеллара (субдифференциал линейной комбинации)
Пусть $f_i(x)$ – выпуклые функции на выпуклых множествах $S_i, ; i = overline{1,n}$.
Тогда, если $bigcaplimits_{i=1}^n mathbf{ri } S_i neq emptyset$ то функция $f(x) = sumlimits_{i=1}^n a_i f_i(x), ; a_i > 0$ имеет субдифференциал $partial_S f(x)$ на множестве $S = bigcaplimits_{i=1}^n S_i$ и
$$
partial_S f(x) = sumlimits_{i=1}^n a_i partial_{S_i} f_i(x)
$$
Важное следствие (субдифференциал максимума)
Пусть $f_i(x)$ – выпуклые функции на открытом выпуклом множестве $S subseteq mathbb{R}^n, ; x_0 in S$, а поточечный максимум определяется как $f(x) = underset{i}{operatorname{max}} f_i(x)$. Тогда:
$$
partial_S f(x_0) = mathbf{conv}left{ bigcuplimits_{i in I(x_0)} partial_S f_i(x_0) right}
$$
где $I(x) = { i in [1:m]: f_i(x) = f(x)}$
Теорема (субдифференциал сложной функции)
Пусть $g_1, ldots, g_m$ – выпуклые функции на открытом выпуклом множестве $S subseteq mathbb{R}^n$, $g = (g_1, ldots, g_m)$ – образованная из них вектор – функция, $varphi$ – монотонно неубывающая выпуклая функция на открытом выпуклом множестве $U subseteq mathbb{R}^m$, причем $g(S) in U$. Тогда субдифференциал функции $f(x) = varphi left( g(x)right)$ имеет вид:
$$
partial f(x) = bigcuplimits_{p in partial varphi(u)} left( sumlimits_{i=1}^{m}p_i partial g_i(x) right),
$$
где $u = g(x)$
Важное следствие
В частности, если функция $varphi$ дифференцируема в точке $u = g(x)$, то формула запишется так:
$$
partial f(x) = sumlimits_{i=1}^{m}dfrac{partial varphi}{partial u_i}(u) partial g_i(x)
$$
Conditional subgradient
Определение
Множество
$$
{ g | f(x) – f(x_0) geq langle g, x – x_0 rangle, ; forall x in S }
$$
называется субдифференциалом $f$ в $x_0$ на множестве $S$ и обозначается $partial_S f(x_0)$.
Примеры
Концептуально, различают три способа решения задач на поиск субградиента:
- Теоремы Моро – Рокафеллара, композиции, максимума
- Геометрически
- По определению
Пример 1
Найти $partial f(x)$, если $f(x) = |x|$
Пример 2
Найти $partial f(x)$, если $f(x) = |x – 1| + |x + 1| $
Пример 3
Найти $partial f(x)$, если $f(x) = left[ max(0, f_0(x))right]^q$. Здесь $f_0(x)$ – выпуклая функция на открытом выпуклом множестве $S$, $q geq 1$.
Решение:
Согласно теореме о композиции (функция $varphi (x) = x^q$ – дифференцируема), а $g(x) = max(0, f_0(x))$ имеем:
$$partial f(x) = q(g(x))^{q-1} partial g(x)$$
По теореме о поточечном максимуме:
$$
partial g(x) = begin{cases} partial f_0(x), ;;; f_0(x) > 0, {0}, ;;;;; f_0(x) < 0 {a mid a = lambda a’, ; 0 le lambda le 1, ; a’ in partial f_0(x), ;; f_0(x) = 0 } end{cases}
$$
Пример 4
Найти $partial f(x)$, если $f(x) = sin x, x in [pi/2; 2pi]$

Пример 5
Найти $partial f(x)$, если $f(x) = |c_1^Tx| + |c_2^Tx| $
Домашнее задание 7
- Докажите, что точка $x_0$ – является точкой минимума выпуклой функции $f(x)$ тогда и только тогда, когда $0 in partial f(x_0)$
- Найти $partial f(x)$, если $f(x) = text{ReLU}(x) = max {0, x}$
- Найти $partial f(x)$, если $f(x) = |x|_p$ при $p = 1,2, infty$
- Найти $partial f(x)$, если $f(x) = |Ax – b|_1^2$
- Найти $partial f(x)$, если $f(x) = e^{|x|}$
Motivation
Важным свойством непрерывной выпуклой функции (f(x)) является то, что в выбранной точке (x_0) для всех (x in text{dom } f) выполнено неравенство:
[f(x) geq f(x_0) + langle g, x – x_0 rangle]
для некоторого вектора (g), то есть касательная к графику функции является глобальной оценкой снизу для функции.
- Если (f(x)) – дифференцируема, то (g = nabla f(x_0))
- Не все непрерывные выпуклые функции дифференцируемы 🙂
Не хочется лишаться такого вкусного свойства.
Вектор (g) называется субградиентом функции (f(x): S to mathbb{R}) в точке (x_0), если (forall x in S):
[f(x) geq f(x_0) + langle g, x – x_0 rangle]
Subdifferential
Множество всех субградиентов функции (f(x)) в точке (x_0) называется субдифференциалом (f) в (x_0) и обозначается (partial f(x_0)).
- Если (x_0 in mathbf{ri } S), то (partial f(x_0)) выпуклое компактное множество.
- Выпуклая функция (f(x)) дифференцируема в точке (x_0Rightarrow partial f(x_0) = {nabla f(x_0)})
- Если (partial f(x_0) neq emptyset ;;; forall x_0 in S), то (f(x)) – выпукла на (S).

Moreau – Rockafellar theorem (subdifferential of a linear combination)
Пусть (f_i(x)) – выпуклые функции на выпуклых множествах (S_i, ; i = overline{1,n}).
Тогда, если (bigcaplimits_{i=1}^n mathbf{ri } S_i neq emptyset) то функция (f(x) = sumlimits_{i=1}^n a_i f_i(x), ; a_i > 0) имеет субдифференциал (partial_S f(x)) на множестве (S = bigcaplimits_{i=1}^n S_i) и
[partial_S f(x) = sumlimits_{i=1}^n a_i partial_{S_i} f_i(x)]
Dubovitsky – Milutin theorem (subdifferential of a point-wise maximum)
Пусть (f_i(x)) – выпуклые функции на открытом выпуклом множестве (S subseteq mathbb{R}^n, ; x_0 in S), а поточечный максимум определяется как (f(x) = underset{i}{operatorname{max}} f_i(x)). Тогда:
[partial_S f(x_0) = mathbf{conv}left{ bigcuplimits_{i in I(x_0)} partial_S f_i(x_0) right},]
где (I(x) = { i in [1:m]: f_i(x) = f(x)})
Chain rule for subdifferentials
Пусть (g_1, ldots, g_m) – выпуклые функции на открытом выпуклом множестве (S subseteq mathbb{R}^n), (g = (g_1, ldots, g_m)) – образованная из них вектор – функция, (varphi) – монотонно неубывающая выпуклая функция на открытом выпуклом множестве (U subseteq mathbb{R}^m), причем (g(S) subseteq U). Тогда субдифференциал функции (f(x) = varphi left( g(x)right)) имеет вид:
[partial f(x) = bigcuplimits_{p in partial varphi(u)} left( sumlimits_{i=1}^{m}p_i partial g_i(x) right),]
где (u = g(x))
В частности, если функция (varphi) дифференцируема в точке (u = g(x)), то формула запишется так:
[partial f(x) = sumlimits_{i=1}^{m}dfrac{partial varphi}{partial u_i}(u) partial g_i(x)]
Subdifferential calculus
- (partial (alpha f)(x) = alpha partial f(x)), for (alpha geq 0)
- (partial (sum f_i)(x) = sum partial f_i (x)), (f_i) – выпуклые функции
- (partial (f(Ax + b))(x) = A^Tpartial f(Ax + b)), (f) – выпуклая функция
- (z in partial f(x)) if and only if (x in partial f^∗(z)).
Examples
Концептуально, различают три способа решения задач на поиск субградиента:
- Теоремы Моро – Рокафеллара, композиции, максимума
- Геометрически
- По определению
1
Найти (partial f(x)), если (f(x) = |x|)
Решение:
Решить задачу можно либо геометрически (в каждой точке числовой прямой указать угловые коэффициенты прямых, глобально подпирающих функцию снизу), либо по теореме Моро – Рокафеллара, рассмотрев (f(x)) как композицию выпуклых функций:
[f(x) = max{-x, x}]
2
Найти (partial f(x)), если (f(x) = |x – 1| + |x + 1|)
Решение:
Совершенно аналогично применяем теорему Моро – Рокафеллара, учитывая следующее:
[partial f_1(x) = begin{cases} -1, &x < 1\ [-1;1], ;;;;; &x = 1 \ 1, &x > 1 end{cases} qquad partial f_2(x) = begin{cases} -1, &x < -1\ [-1;1], &x = -1 \ 1, &x > -1 end{cases}]
Таким образом:
[partial f(x) = begin{cases} -2, &x < -1\ [-2;0], &x = -1 \ 0, &-1 < x < 1 \ [0;2], &x = 1 \ 2, &x > 1 \ end{cases}]
3
Найти (partial f(x)), если (f(x) = left[ max(0, f_0(x))right]^q). Здесь (f_0(x)) – выпуклая функция на открытом выпуклом множестве (S), (q geq 1).
Решение:
Согласно теореме о композиции (функция (varphi (x) = x^q) – дифференцируема), а (g(x) = max(0, f_0(x))) имеем: (partial f(x) = q(g(x))^{q-1} partial g(x))
По теореме о поточечном максимуме:
[partial g(x) = begin{cases} partial f_0(x), quad f_0(x) > 0,\ {0}, quad f_0(x) < 0 \ {a mid a = lambda a’, ; 0 le lambda le 1, ; a’ in partial f_0(x)}, ;; f_0(x) = 0 end{cases}]
4
Найти (partial f(x)), если (f(x) = sin x, x in [pi/2; 2pi])

5
Найти (partial f(x)), если (f(x) = |c_1^top x| + |c_2^top x|)
Решение: Пусть (f_1(x) = |c_1^top x|), а (f_2(x) = |c_2^top x|). Так как эти функции выпуклы, субдифференциал их суммы равен сумме субдифференциалов. Найдем каждый из них:
(partial f_1(x) = partial left( max {c_1^top x, -c_1^top x} right) = begin{cases} -c_1, &c_1^top x < 0\ mathbf{conv}(-c_1;c_1), &c_1^top x = 0 \ c_1, &c_1^top x > 0 end{cases}) (partial f_2(x) = partial left( max {c_2^top x, -c_2^top x} right) = begin{cases} -c_2, &c_2^top x < 0\ mathbf{conv}(-c_2;c_2), &c_2^top x = 0 \ c_2, &c_2^top x > 0 end{cases})
Далее интересными представляются лишь различные взаимные расположения векторов (c_1) и (c_2), рассмотрение которых предлагается читателю.
6
Найти (partial f(x)), если (f(x) = | x|_1)
Решение: По определению
[|x|_1 = |x_1| + |x_2| + ldots + |x_n| = s_1 x_1 + s_2 x_2 + ldots + s_n x_n]
Рассмотрим эту сумму как поточечный максимум линейных функций по (x): (g(x) = s^top x), где (s_i = { -1, 1}). Каждая такая функция однозначно определяется набором коэффициентов ({s_i}_{i=1}^n).
Тогда по теореме Дубовицкого – Милютина, в каждой точке (partial f = mathbf{conv}left(bigcuplimits_{i in I(x)} partial g_i(x)right))
Заметим, что (partial g(x) = partial left( max {s^top x, -s^top x} right) = begin{cases} -s, &s^top x < 0\ mathbf{conv}(-s;s), &s^top x = 0 \ s, &s^top x > 0 end{cases}).
Причем, правило выбора “активной” функции поточечного максимума в каждой точке следующее:
- Если j-ая координата точки отрицательна, (s_i^j = -1)
- Если j-ая координата точки положительна, (s_i^j = 1)
- Если j-ая координата точки равна нулю, то подходят оба варианта коэффициентов и соответствующих им функций, а значит, необходимо включать субградиенты этих функций в объединение в теореме Дубовицкого – Милютина.
В итоге получаем ответ:
[partial f(x) = left{ g ; : ; |g|_infty leq 1, quad g^top x = |x|_1 right}]
References
- Lecture Notes for ORIE 6300: Mathematical Programming I by Damek Davis
Содержание
- 1 Используемые определения
- 2 Определение субдифференциала
- 3 Вспомогательные утверждения
- 4 Структура субдифференциала выпуклой функции
- 5 Пример к теореме 2
- 6 Теорема Моро-Рокафеллара
- 7 Критерий дифференцируемости
- 8 Список литературы

Пусть $$X = mathbb{R}^n$$ и $$f -$$ собственная выпуклая функция
На графике приведен пример выпуклой функции, которая недифференцируема в точке $$x = 0$$ (на графике показано множество касательных в этой точке).
Используемые определения
Функция $$f$$ называется собственной, если dom $$f neq varnothing$$ и $$f(x) > -infty~~forall x$$, где $$text{dom f} = {x in X: f(x) < +infty} -$$ эффективное множество функции $$f$$.
Субградиентом функции $$f$$ в точке $$x$$ называется вектор $$x^* in X$$ такой, что $$f(y) geqslant f(x) + langle x^*,y – x rangle~~forall y in X$$. Это неравенство называется субградиентным неравенством.
Определение субдифференциала
Субдифференциалом функции $$f$$ в точке $$x$$ называется множество всех субградиентов функции $$f$$ в этой точке. Субдифференциал обозначается $$partial f(x)$$.
Например, на графике выше $$partial f(0) = [-1,1]$$.
Заметим, что функция $$f$$ достигает в точке $$x$$ минимума тогда и только тогда, когда $$0 in partial f(x)$$.
Вспомогательные утверждения
Теорема 1.
Пусть функция $$f$$ выпукла и конечна в точке $$x$$. Тогда
[
f'(x,y) = inf limits_{lambda > 0} dfrac{f(x + lambda y) – f(x)}{lambda}
]
(где $$f'(x,y) – $$ производная $$f(x)$$ по направлению $$y$$), функция $$f'(x, cdot)$$ выпукла, положительно однородна и
[
f'(x,0) = 0, -f'(x, -y) leqslant f'(x,y)~~forall y.
]
Доказательство:
Для удобства будем считать, что $$x = 0, f(x) = 0$$. Для $$lambda > 0$$ положим $$h(y) = dfrac{f(lambda y)}{lambda}$$. Покажем, что функция $$h(cdot)$$ не убывает. Действительно, пусть $$0 < mu < lambda$$. Тогда в силу выпуклости $$f$$ имеем $$f(mu y) = fleft(0left(1 – dfrac{mu}{lambda}right) + dfrac{mu}{lambda} lambda yright) leqslant f(0)left( 1 – dfrac{mu}{lambda} right) + f(lambda y)dfrac{mu}{lambda} = f(lambda y)dfrac{mu}{lambda} Rightarrow dfrac{f(mu y)}{mu} leqslant dfrac{f(lambda y)}{lambda}$$ и, значит, $$h$$ не убывает. Поэтому $$lim limits_{lambda to 0+} h(lambda) = inf limits_{lambda > 0} h(lambda) = f'(0, y).$$
Пусть дано $$mu geqslant 0$$. Тогда, очевидно, $$dfrac{f(lambda(mu y))}{lambda} = mu dfrac{f(chi y)}{chi} = mu h(chi)$$, где $$chi = lambda mu$$. Поэтому $$f'(0, (mu y)) = mu lim limits_{chi to 0+} h(chi) = mu f'(0, y)$$ и, значит, функция $$f'(0, cdot)$$ положительно однородна, $$f'(0,0) = 0$$ по определению.
Докажем выпуклость функции $$f'(x, cdot)$$. Пусть $$alpha, beta geqslant 0, alpha + beta = 1, y_1, y_2 in X$$. В силу выпуклости $$f$$ имеем
[
f'(x, alpha y_1 + beta y_2) = lim limits_{lambda to 0+} dfrac{f(x + lambda alpha y_1 + lambda beta y_2) – f(x)}{lambda} leqslant
]
[
leqslant lim limits_{lambda to 0+} dfrac{alpha f(x + lambda y_1) + beta f(x + lambda y_2) – alpha f(x) – beta f(x)}{lambda} =
]
[
= lim limits_{lambda to 0+} alpha dfrac{f(x + lambda y_1) – f(x)}{lambda} + lim limits_{lambda to 0+} beta dfrac{f(x + lambda y_2) – f(x)}{lambda} = alpha f'(x, y_1) + beta f'(x, y_2).
]
Значит, функция $$f'(x, cdot)$$ выпукла. Из ее выпуклости и положительной однородности получаем $$f'(x,y) + f'(x, -y) geqslant 2f'(x, frac{y + (-y)}{2}) = 2f'(x,0) = 0$$, откуда имеем $$-f'(x,-y) leqslant f'(x,y)$$. $$blacksquare$$
Лемма 1.
Пусть $$f -$$ собственная выпуклая функция и $$x in text{int}(text{dom }f)$$. Тогда существует $$c > 0$$ такое, что
[
|f'(x,y)| leqslant c|y|~~forall y,
]
где $$text{int A} -$$ внутренность множества$$A -$$ множество всех внутренних точек множества $$A$$.
Доказательство:
По теореме о липшицевости выпуклой функции существует такая окрестность $$O$$ точки $$x$$, что функция $$f$$ на $$O$$ удовлетворяет условию Липшица с некоторой константой $$c > 0$$. Поэтому для каждого фиксированного $$y$$ неравенство $$left| dfrac{f(x + lambda y) – f(x)}{lambda} right| leqslant c|y|$$ выполняется при всех достаточно малых $$lambda > 0$$. Искомое утверждение непосредственно вытекает из этого неравенства и соотношения
[
f'(x,y) = lim limits_{lambda to 0+} dfrac{f(x + lambda y) – f(x)}{lambda}.blacksquare
]
Лемма 2.
Пусть функция $$f$$ выпукла и конечна в точке $$x$$. Тогда
[
x^* in partial f(x) Leftrightarrow f'(x,y) geqslant langle x^*, y rangle~~forall y in X.
]
Доказательство:
Пусть $$x^* in partial f(x)$$. Тогда в силу субградиентного неравенства при всяком $$lambda > 0$$ имеем $$f(x + lambda y) – f(x) geqslant langle x^*, y rangle~~forall y$$ и, значит,
[
f'(x,y) = lim limits_{lambda to 0+} dfrac{f(x + lambda y) – f(x)}{lambda} geqslant langle x^*, y rangle.
]
Теперь пусть
[
langle x^*, y rangle leqslant f'(x,y) = inf limits_{lambda > 0} dfrac{f(x + lambda y) – f(x)}{lambda}~~forall y Rightarrow
]
[
Rightarrow f(x + lambda y) – f(x) geqslant langle x^*, y rangle~~forall y in X,~~forall lambda > 0.
]
Отсюда при $$lambda = 1, z = x + y$$ имеем $$f(z) – f(x) geqslant langle x^*, z – x rangle~~forall z in X$$, откуда $$x^* in partial f(x)$$. $$blacksquare$$
Лемма 3.
Пусть функция $$f$$ выпуклая, собственная и $$x in text{int}(text{dom }f)$$. Тогда функция $$text{cl }f'(x,cdot)$$, являющаяся замыканием производной $$f'(x,y)$$ как выпуклой функции от $$y$$, совпадает c опорной функцией множества $$partial f(x)$$, где $$text{cl }A -$$ замыкание множества $$A$$.
Доказательство:
По теореме 1 и лемме 1 функция $$f'(x,cdot)$$ является выпуклой, положительно однородной и собственной. Поэтому имеет место $$text{cl }f'(x,cdot) = rho(cdot, A)$$, где $$A = {x^*: langle x^*, y rangle leqslant f'(x,y)~~forall y}$$. По лемме 2: $$A = partial f(x)$$. $$blacksquare$$
Лемма 4.
Для любых функций $$f_1,…,f_k$$ имеет место
[
partial (f_1+…+f_k)(x) supseteq partial f_1(x) +…+ partial f_k(x)~~forall x in X.
]
Доказательство:
Пусть $$x^* in partial f_1(x) +…+ partial f_k(x)$$. Тогда $$x^* = x_1^* +…+ x_k^*$$, где $$x_i^* in partial f_i(x)$$. Поэтому
[
f_1(y) geqslant f_1(x) + langle x_1^*,y-x rangle,…,f_k(y) geqslant f_k(x) + langle x_k^*,y-x rangle~~forall y in X.
]
Складывая при каждом фиксированном $$y$$ все эти неравенства, получаем, что $$x^* in partial (f_1+…+f_k)(x)$$.$$blacksquare$$
Структура субдифференциала выпуклой функции
Теорема 2.
Пусть $$f -$$ выпуклая собственная функция и $$x in text{int}(text{dom }f)$$. Тогда субдифференциал $$partial f(x)$$ в точке $$x$$ является непустым компактом.
Доказательство:
Вначале докажем, что $$partial f(x) neq varnothing.$$ Рассмотрим множество $$text{cl epi }f (text{epi }f = {(x, alpha) in X times mathbb{R}: f(x) leqslant alpha} -$$ надграфик функции $$f$$). Оно выпукло, замкнуто, и $$(x, f(x)) notin text{int}(text{cl epi }f).$$ Здесь несложно показать, что последнее утверждение вытекает из непрерывности на $$text{int}(text{dom }f)$$ определенной на $$mathbb{R}^n$$ выпуклой собственной функции. Поэтому по теореме отделимости существуют $$x^* in mathbb{R}^n, r in mathbb{R}$$ такие, что
[
ralpha + langle x^*, z rangle geqslant rf(x) + langle x^*, x rangle ; forall alpha, z: alpha geqslant f(z).
]
Условие $$r neq 0$$ вытекает из того, что $$x in text{int}(text{dom }f)$$. Условие $$r > 0$$ следует из того, что приведенное неравенство выполняется при сколь угодно больших $$alpha geqslant f(z)$$. Поэтому, не теряя общности, будем считать, что $$r = 1$$. Из приведенного неравенства при $$alpha = f(z)$$ имеем
[
f(z) geqslant f(x) + langle -x^*, z-x rangle ; forall z Rightarrow -x^* in partial f(x)
]
и, значит, $$partial f(x) neq varnothing$$.
Докажем ограниченность множества $$partial f(x)$$. Действительно, предположим обратное, т. е. что в $$partial f(x)$$ существует такая последовательность $${x^*_i}$$, что $$|x^*_i| rightarrow infty$$. Выберем такое $$delta > 0$$, что $$text{cl}(O(x, delta)) subset text{int}(text{dom }f)$$. Тогда функция $$f$$ непрерывна и, значит, ограничена на компакте $$text{cl}(O(x, delta))$$. Положим $$x_i = x + delta x^*_i/|x^*_i|$$. Из субградиентного неравенства при $$y = x_i$$ и $$x^* = x^*_i$$ получаем что $$f(x_i) geqslant f(x) + delta|x^*_i|$$. Но в полученном неравенстве правая часть стремится к бесконечности, а левая ограничена, поскольку $$x_i in text{cl}(O(x, delta)) ; forall i$$. Это противоречие доказывает ограниченность множества $$partial f(x)$$.
Докажем замкнутость множества $$partial f(x)$$. Пусть $$x^*_i in partial f(x) ; forall i$$ и $$x^*_i rightarrow x^*$$. При каждом фиксированном $$y$$, подставляя в субградиентное неравенство $$x^* = x^*_i$$ и переходя к пределу при $$i rightarrow infty$$,
получаем $$x^* in partial f(x)$$.
Осталось доказать выпуклость множества $$partial f(x)$$. Пусть $$x_1^*, x_2^* in partial f(x), alpha geqslant 0, beta geqslant 0, alpha + beta = 1$$. Тогда:
[
f(z) – f(x) geqslant langle x_1^*, z – x rangle, ; f(z) – f(x) geqslant langle x_2^*, z – x rangle ; forall z in X.
]
При фиксированном $$z$$ умножим первое из этих неравенств на $$alpha$$, а второе на $$beta$$, и затем сложим их. В результате этого получаем, что $$alpha x_1^* + beta x_2^* in partial f(x). blacksquare$$
Лемма 5 (альтернатива). Пусть выпуклая функция $$f$$ конечна в точке $$x_0$$, принадлежащей границе эффективного множества $$text{dom }f$$. Тогда в этой точке субдифференциал $$partial f(x_0)$$ либо пуст, либо содержит бесконечно много точек.
Доказательство:
В силу выпуклости субдифференциала $$partial f(x_0)$$ достаточно доказать, что если это множество непусто, то оно содержит хотя бы два различных элемента. Итак, пусть $$x^* in partial f(x_0)$$. Рассмотрим выпуклую функцию $$h(y) = f(x_0 + y) – f(x_0) – langle x^*,y rangle$$. Для нее $$h(0) = 0$$, и нуль принадлежит границе эффективного множества $$text{dom }h$$. Кроме того, $$0 in partial h(0)$$, откуда в силу субградиентного неравенства получаем, что $$h(y) geqslant 0 ~~forall y in X$$.
В силу сказанного выше $$0 notin text{int(dom }h)$$. Поэтому выпуклое множество $$text{dom }h$$ можно отделить от нуля и, значит, в силу конечномерной теоремы отделимости существует такой $$a in X, a neq 0$$ что $$langle a,y rangle leqslant 0 ~~forall y in text{dom }h.$$ Следовательно, $$h(y) geqslant langle a,y rangle ~~forall y in X,$$ поскольку $$h(y) geqslant 0 ~~forall y in X.$$ Значит, $$0,a in partial h(0), a neq 0 Rightarrow x^*, (a + x^*) in partial f(x_0)$$. $$blacksquare$$
Лемма 6 (бесконечномерная альтернатива). Пусть $$X -$$ произвольное нормированное пространство, а заданная на нем выпуклая функция $$f$$ конечна в точке $$x_0$$, принадлежащей границе эффективного множества $$text{dom }f$$, и, кроме того, внутренность эффективного множества $$text{int(dom }f)$$ непуста. Тогда в этой точке субдифференциал $$partial f(x_0)$$ либо пуст, либо содержит бесконечно много точек.
Доказательство:
Доказательство этой леммы аналогично доказательству предыдущей, но вместо теоремы о конечномерной отделимости следует использовать теорему отделимости. $$blacksquare$$
Пример к теореме 2
Рассмотрим на $$mathbb{R}$$ функцию
[
f(x) =
begin{cases}
-(1 – x^2)^{frac{1}{2}}, & quad |x| leqslant 1,\
+infty, & quad |x| > 1.
end{cases}
]
Эта функция субдифференцируема (и даже дифференцируема) во всех точках $$x in text{int}(text{dom }f) = (-1,1)$$. Однако в точках $$x = 1, -1$$, составляющих границу $$text{dom }f$$, ее субдифференциал пуст.
Теорема Моро-Рокафеллара
Теорема 3 (Моро-Рокафеллара).
Пусть функции $$f_1,…,f_k$$ являются собственными и выпуклыми, причем существует точка $$x_0 in cap_i text{dom } f_i$$, в которой все функции $$f_i$$, за исключением, возможно, одной, непрерывны.
Тогда имеет место
[
partial (f_1+…+f_k)(x) = partial f_1(x) +…+ partial f_k(x)~~forall x in X.
]
Доказательство:
Приведем доказательство только для случая $$k = 2$$ (общий случай доказывается по индукции). Исходя из предыдущего утверждения, достаточно показать, что
[
partial (f_1+f_2)(x) subset partial f_1(x) + partial f_2(x)~~forall x in X.
]
По условию в точке $$x_0 in text{dom } f_1 cap text{dom } f_2$$ хотя бы одна из рассматриваемых функций, пусть для определенности это $$f_1$$, непрерывна. Тогда $$x_0 in text{int(dom } f_1)$$ и, значит, пересечение множеств $$text{int(dom } f_1)$$ и $$text{dom } f_2$$ непусто.
Зафиксируем $$x in X$$. Возьмем произвольное $$x^* in partial(f_1+f_2)(x)$$. Заменяя, если необходимо, функции $$f_1, f_2$$ собственными выпуклыми функциями
[
g_1(z) = f_1(x+z) – f_1(x) – langle x^*,z rangle, g_2(z) = f_2(x+z) – f_2(x),
]
будем считать, не ограничивая общности, что
[
x = 0, f_1(0) = 0, f_2(0) = 0, x^* = 0.
]
Итак, $$0 in partial (f_1 + f_2)(0)$$. Докажем, что $$0 in partial f_1(0) + partial f_2(0)$$.
Действительно, в силу сделанного предположения
begin{equation}
label{1}
f_1(z) + f_2(z) geqslant f_1(0) + f_2(0) = 0~~forall z in X.
end{equation}
Рассмотрим множества
[
C_1 = {(z,mu): mu geqslant f_1(z)}, C_2 = {(z,mu): mu < -f_2(z)}.
]
Из выпуклости функций $$f_1,f_2$$ непосредственно вытекает, что оба эти множества выпуклы. Кроме того, они не пересекаются, ибо иначе в некоторой точке $$z$$ выполнялось бы неравенство $$-f_2(z) > f_1(z)$$, которое, в свою очередь, противоречило бы $$ref{1}$$. Таким образом, выпуклые множества $$C_1$$ и $$C_2$$ не пересекаются. Поэтому по теореме отделимости для конечномерных пространств эти два множества можно отделить, т.е. существуют такие одновременно неравные нулю $$z^* in mathbb{R}^n$$ и $$beta in mathbb{R}$$, что
begin{equation}
label{2}
sup limits_{(z,mu) in C_1} (beta mu + langle z^*,z rangle) leqslant inf limits_{(z,mu) in C_2} (beta mu + langle z^*,z rangle).
end{equation}
Очевидно, $$beta leqslant 0$$, ибо при $$beta > 0$$ верхняя грань в $$ref{2}$$ равнялась бы $$+infty$$, а нижняя грань равнялась бы $$-infty$$. Случай $$beta = 0$$ также невозможен, так как если $$beta = 0$$, то $$z^* neq 0$$ и $$ref{2}$$ принимает вид
[
sup limits_{z in text{dom }f_1} langle z^*,z rangle leqslant inf limits_{z in text{dom }f_2} langle z^*,z rangle.
]
А это противоречит тому, что пересечение множеств $$text{int(dom }f_1)$$ и $$text{dom }f_2$$ непусто. Таким образом, доказано, что $$beta < 0$$, и поэтому, не ткряя общности, будем считать $$beta = -1$$.
Из $$ref{2}$$ следует неравенство
[
sup limits_z {langle z^*,z rangle – f_1(z)} leqslant inf limits_z {langle z^*,z rangle – f_2(z)}.
]
Но при $$z = 0$$ выражения в фигурных скобках как в левой, так и в правой частях этого неравенства обращаются в нуль.
Поэтому получаем
[
f_1(z) geqslant langle z^*,z rangle, f_2(z) geqslant langle -z^*,z rangle~~forall z in X.
]
Итак,
[
f_1(z) geqslant f_1(0) + langle z^*,z – 0 rangle~~forall z in X,
]
[
f_2(z) geqslant f_2(0) + langle -z^*,z – 0 rangle~~forall z in X.
]
Значит, $$z^* in partial f_1(0), -z^* in partial f_2(0)$$; следовательно, $$0 in partial f_1(0) + partial f_2(0)$$.$$blacksquare$$
Критерий дифференцируемости
Теорема 4.
Пусть выпуклая функция $$f$$ конечна в точке $$x_0$$. Если $$f$$ дифференцируема в точке $$x_0$$, то субдифференциал $$partial f(x_0)$$ содержит единственный элемент $$f'(x_0)$$ и, в частности,
[
f(z) geqslant f(x_0) + langle f'(x_0), z – x_0 rangle~~forall z in X.
]
Наоборот, если субдифференциал $$partial f(x_0)$$ содержит единственный элемент, то функция $$f$$ дифференцируема в точке $$x_0$$ и $$partial f(x_0) = {f'(x_0)}$$.
Доказательство:
Пусть $$f$$ дифференцируема в точке $$x_0$$. Тогда $$f'(x_0,y) = langle f'(x_0),y rangle~~forall y$$. Поэтому в силу леммы 2 для любого $$x^* in partial f(x_0)$$ выполняется
[
langle f'(x_0),y rangle = f'(x_0,y) geqslant langle x^*,y rangle~~forall y in X,
]
откуда
[
langle (f'(x_0) – x^*),y rangle geqslant 0 rangle~~forall y in X.
]
Но если линейный функционал неотрицателен на всем пространстве, то он равен нулю и, следовательно, $$x^* = f'(x_0)~~forall x^* in partial f(x_0)$$, т.е. субдифференциал $$partial f(x_0)$$ состоит из единственной точки $$f'(x_0)$$.
Пусть теперь $$partial f(x_0) = {x^*}$$. Рассмотрим выпуклую функцию $$h(y) = f(x_0 + y) – f(x_0) – langle x^*,y rangle$$. Для нее $$h(0) = 0, partial h(0) = {0}$$, откуда в силу субградиентного неравенства получаем $$h(y) geqslant 0~~forall y in X$$ и, значит, функция $$h$$ является собственной. Кроме того, в силу леммы 5 имеет место $$0 in text{int}(text{dom }h)$$. Поэтому согласно лемме 3 функция $$text{cl }h'(0,cdot)$$ является опорной функцией для множества $$partial h(0)$$. Таким образом, $$text{cl }h'(0,y) = rho(y, partial h(0)) = 0~~forall y in X$$.
Итак, $$0 in text{int}(text{dom }h)$$, а $$h -$$ собственная выпуклая функция. Поэтому в силу леммы 1 выпуклая функция $$h'(0,cdot)$$ принимает лишь конечные значения и, следовательно, она непрерывна на $$mathbb{R}^n$$. Поэтому в силу доказанного выше $$h'(0,y) equiv 0$$. Следовательно,
[
lim limits_{lambda to 0+} dfrac{h(lambda y)}{lambda} = 0~~forall y in X.
]
Кроме того, из доказательства теоремы 1 вытекает, что при каждом фиксированном $$y$$ функция $$g(lambda) = dfrac{h(lambda y)}{lambda}$$ не убывает при $$lambda > 0$$.
При произвольном $$lambda > 0$$ рассмотрим функцию $$g_{lambda}(u) = dfrac{h(lambda y)}{lambda}$$. Каждая из функций $$g_{lambda}$$ выпукла, и для любого $$u$$ в силу доказанного имеем: $$g_{lambda}(u) to 0, lambda to 0+, g_{lambda}(u) geqslant 0$$. Пусть $$B = {x: |x| leqslant 1} -$$ единичный шар, а $${b_1,…,b_m} -$$ конечный набор точек, выпуклая оболочка которых содержит $$B$$.
Всякое $$u in B$$ можно представить в виде выпуклой комбинации $$u = alpha_1 b_1 +…+ alpha_m b_m$$. Следовательно, в силу выпуклости каждой из функций $$g_{lambda}$$, для любого $$u in B$$ имеет место
[
0 leqslant g_{lambda}(u) leqslant alpha_1 g_{lambda}(b_1) +…+ alpha_m g_{lambda}(b_m) leqslant max{g_{lambda}(b_i), i = 1,…,m}.
]
Тогда, поскольку $$g_{lambda}(b_i) to 0. lambda to 0+$$ для каждого $$i$$, функция $$g_{lambda}$$ сходятся к нулю равномерно на $$B$$. Поэтому для любого $$varepsilon > 0$$ существует $$delta > 0$$ такое, что
[
dfrac{h(lambda u)}{lambda} leqslant varepsilon~~forall lambda in (0, delta],~~forall in B.
]
Но любой вектор $$y neq 0, |y| leqslant delta$$ можно представить в виде $$y = lambda u$$, где $$lambda = |y| leqslant delta, u = dfrac{y}{|y|} in B$$. Поэтому неравенство $$dfrac{h(y)}{|y|} leqslant varepsilon$$ выполняется при всех $$y$$, для которых $$|y| leqslant delta$$.
Таким образом, мы доказали, что $$dfrac{h(y)}{|y|} to 0, y to 0$$. Иными словами, функция $$h$$ дифференцируема в нуле, причем ее производная равна нулю. Значит, $$f$$ дифференцируема в точке $$x_0$$. $$blacksquare$$
Список литературы
Арутюнов А. В. Лекции по выпуклому и многозначному анализу. — М.: ФИЗМАТЛИТ, 2014




