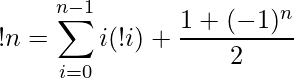Как найти субфакториал числа

Как найти субфакториал числа

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016 года; проверки требуют 19 правок.

Субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.

В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (так называемая «Задача о письмах»).

Явная формула[править | править код]

Субфакториал можно вычислить с помощью принципа включения-исключения:

!n=n!left(1-{frac {1}{1!}}+{frac {1}{2!}}-{frac {1}{3!}}+...+(-1)^{n}{frac {1}{n!}}right)=n!sum _{{k=0}}^{n}{frac {(-1)^{k}}{k!}}

Другие формулы[править | править код]

Таблица значений[править | править код]

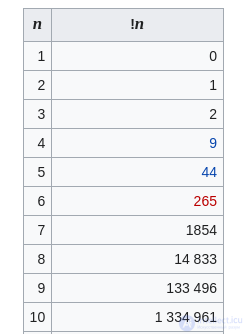
n !n[1]
1 0
2 1
3 2
4 9
5 44
6 265
7 1854
8 14 833
9 133 496
10 1 334 961
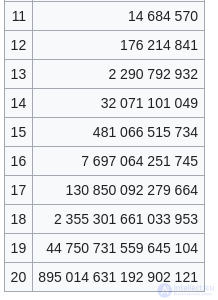
11 14 684 570
12 176 214 841
13 2 290 792 932
14 32 071 101 049
15 481 066 515 734
16 7 697 064 251 745
17 130 850 092 279 664
18 2 355 301 661 033 953
19 44 750 731 559 645 104
20 895 014 631 192 902 121

Свойства[править | править код]

где ;a_{0}=a_{1}=1 и {displaystyle a_{n}=ncdot a_{n-1}+(n-1)cdot a_{n-2}={!(n+1)}+{!n}}. Начальные члены последовательности a_n[2]:

1, 1, 3, 11, 53, 309, 2119, …
  • Число 148 349 является субфакторионом, т.е. равно сумме субфакториалов своих цифр (аналог факториона):
{displaystyle 148349={!1}+{!4}+{!8}+{!3}+{!4}+{!9}}
(найдено J. S. Madachy, 1979)
  • Субфакториал иногда допускается в математических играх типа получения различных результатов из определённых цифр (например, известна игра Четыре четвёрки, где равенство !4 = 9 может принести пользу).

Примечания[править | править код]

  1. ↑ Последовательность A000166 в OEIS = Subfactorial or rencontres numbers, or derangements: number of permutations of n elements with no fixed points
  2. ↑ Последовательность A000255 в OEIS = a(n) counts permutations of [1,…,n+1] having no substring [k,k+1]
Источник

Improve Article

Save Article

Like Article

  • Read
  • Discuss

    • Improve Article

    Save Article

    Like Article

    Given an integer N, the task is to find the subfactorial of the number represented as !N. The subfactorial of a number is defined using below recurrence relation of a number N:

    !N = (N-1) [ !(N-2) + !(N-1) ]

    where !1 = 0 and !0 = 1

    Some of the subfactorials are:

    n 0 1 2 3 4 5 6 7 8 9 10 11 12 13
    !n 1 0 1 2 9 44 265 1, 854 14, 833 133, 496 1, 334, 961 14, 684, 570 176, 214, 841 2, 290, 792, 932

    Examples:

    Input: N = 4
    Output: 9
    Explanation: 
    !4 = !(4-1)*4 + (-1)4 = !3*4 + 1
    !3 = !(3 – 1)*3 + (-1)3 = !2*3 – 1
    !2 = !(2 – 1)*2 + (-1)2 = !1*2 + 1
    !1 = !(1 – 1)*1 + (-1)1 = !0*1 – 1
    Since !0 = 1, therefore !1 = 0, !2 = 1, !3 = 2 and !4 = 9. 

    Input: N = 0
    Output: 1

    Approach: The subfactorial of the number N can also be calculated as:

    {displaystyle !n={begin{cases}1&{text{if }}n=0, \nleft(!(n-1)right)+(-1)^{n}&{text{if }}n>0.end{cases}}}

    Expanding this gives

    {displaystyle !n=sum _{i=0}^{n-1}i(!i)+{frac {1+(-1)^{n}}{2}}}

    => !N = ( N! )*( 1 – 1/(1!) + (1/2!) – (1/3!)  …….. (1/N!)*(-1)N )

    Therefore the above series can be used to find the subfactorial of number N. Follow the steps below to see how:

    • Initialize variables, say res = 0, fact = 1 and count = 0.
    • Iterate over the range from 1 to N using i and do the following:
      • Update fact as fact*i.
      • If the count is even then update res as res = res – (1 / fact).
      • If the count is odd then update res as res = res + (1 / fact).
      • Increase the value of count by 1.
    • Finally, return fact*(1 + res).

    Below is the implementation of the above approach:

    C++

    #include <iostream>

    using namespace std;

    double subfactorial(int N)

    {

        double res = 0, fact = 1;

        int count = 0;

        for (int i = 1; i <= N; i++) {

            fact = fact * i;

            if (count % 2 == 0)

                res = res - (1 / fact);

            else

                res = res + (1 / fact);

            count++;

        }

        return fact * (1 + res);

    }

    int main()

    {

        int N = 4;

        cout << subfactorial(N);

        return 0;

    }

    Java

    import java.util.*;

    class GFG {

        static double subfactorial(int N)

        {

            double res = 0, fact = 1;

            int count = 0;

            for (int i = 1; i <= N; i++) {

                fact = fact * i;

                if (count % 2 == 0)

                    res = res - (1 / fact);

                else

                    res = res + (1 / fact);

                count++;

            }

            return fact * (1 + res);

        }

        public static void main(String[] args)

        {

            int N = 4;

            System.out.println((int)(subfactorial(N)));

        }

    }

    Python3

    def subfactorial(N):

        res = 0

        fact = 1

        count = 0

        for i in range(1, N+1):

            fact = fact * i

            if (count % 2 == 0):

                res = res - (1 / fact)

            else:

                res = res + (1 / fact)

            count += 1

        return fact * (1 + res)

    if __name__ == "__main__":

        N = 4

        print(subfactorial(N))

    C#

    /// C# program for the above approach

    using System;

    using System.Collections.Generic;

    class GFG{

    static double subfactorial(int N)

    {

        double res = 0, fact = 1;

        int count = 0;

        for (int i = 1; i <= N; i++) {

            fact = fact * i;

            if (count % 2 == 0)

                res = res - (1 / fact);

            else

                res = res + (1 / fact);

            count++;

        }

        return fact * (1 + res);

    }

    public static void Main()

    {

        int N = 4;

        Console.Write(subfactorial(N));

    }

    }

    Javascript

    <script>

            function subfactorial(N) {

                let res = 0, fact = 1;

                let count = 0;

                for (let i = 1; i <= N; i++) {

                    fact = fact * i;

                    if (count % 2 == 0)

                        res = res - 1 / fact;

                    else

                        res = res + 1 / fact;

                    count++;

                }

                return fact * (1 + res);

            }

            let N = 4;

            document.write(subfactorial(N));

        </script>

    Time Complexity: O(N)
    Auxiliary Space: O(1)

    Last Updated :
    08 Oct, 2021

    Like Article

    Save Article

    Источник

    Привет, сегодня поговорим про субфакториал, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
    субфакториал , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..


    субфакториал     числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.

    В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (т. н. Задача о письмах).

    Субфакториал — это математическая функция, которая определяется как количество перестановок из n элементов, которые не имеют ни одной фиксированной точки. Символически субфакториал обозначается как !n.

    Например, если у нас есть три элемента {1, 2, 3}, то мы можем получить 3! = 6 перестановок: (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). Однако, если мы хотим получить перестановки без фиксированных точек, то они могут быть только две: (2,3,1) и (3,1,2). Это означает, что !3 = 2.

    Явная формула

    Субфакториал можно вычислить с помощью принципа включения-исключения:

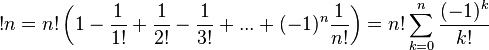
    Субфакториал в математике, понятие и применение

    Другие формулы

    Таблица значений

    Субфакториал в математике, понятие и применение Субфакториал в математике, понятие и применение

    последовательность A000166 в OEIS

    Свойства субфакториала

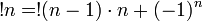
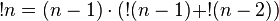    • Субфакториал в математике, понятие и применение
    • Субфакториал в математике, понятие и применение (таким же свойством обладает сам факториал)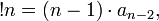
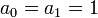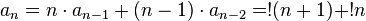    • Субфакториал в математике, понятие и применение

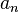    где Субфакториал в математике, понятие и применение и Субфакториал в математике, понятие и применение . Об этом говорит сайт https://intellect.icu . Начальные члены последовательности Субфакториал в математике, понятие и применение:

    1, 1, 3, 11, 53, 309, 2119, … (последовательность A000255 в OEIS)

    • Число 148349 является субфакторионом, т.е равно сумме субфакториалов своих цифр (аналог факториона):

    Субфакториал в математике, понятие и применение (найдено J. S. Madachy, 1979)

    Применение субфакториала

    Итак, если факториал определяет количество перестановок, возможных в наборе из n объектов, то субфакториал характеризует количество беспорядков в таком же наборе. Проще всего понять, что такое факториал на жизненном примере. Возьмем некоторое количество писем и конвертов и пронумеруем их:

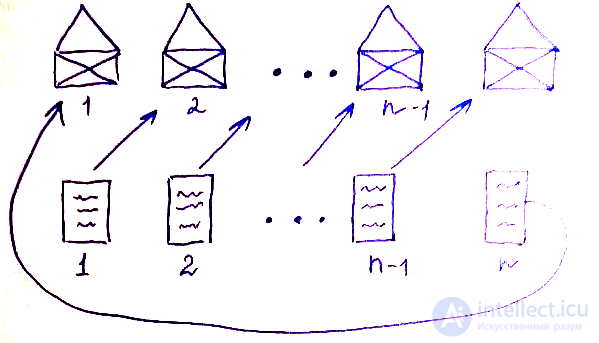
    Субфакториал в математике, понятие и применение

    Теперь наша задача в том, чтобы создать максимальный беспорядок, а именно сделать так, чтобы каждое письмо оказалось не в том конверте, для которого предназначено. На рисунке я показал один из способов такого распределения.

    Вы уже, наверное, догадались, что именно субфакториал определит количество таких возможных перестановок, в комбинаторике называемых смещениями.

    Формула для вычисления субфакториала сложностью не отличается:

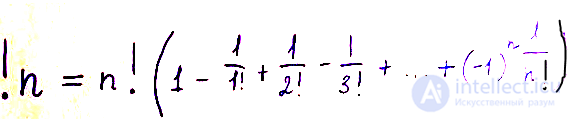
    Субфакториал в математике, понятие и применение

    Формула была выведена Николаем Бернулли еще в 1713 году.

    Единственное, что восклицательный знак ставится перед переменной. Для примера вычислим !4:

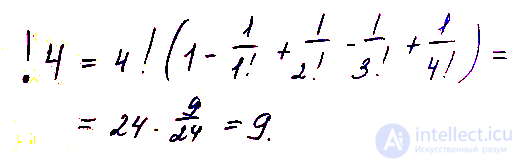
    Субфакториал в математике, понятие и применение

    Значит, в наборе из 4 писем есть 9 вариантов навести тотальный хаос!

    Еще одна интерпретация задачи: профессор дал тест 4 студентам – 1, 2, 3 и 4 – и хочет, чтобы они оценили тесты друг друга. Конечно, ни один студент не должен оценивать свой собственный тест. Сколько существует способов, чтобы никто не получил обратно свой собственный тест для проверки?

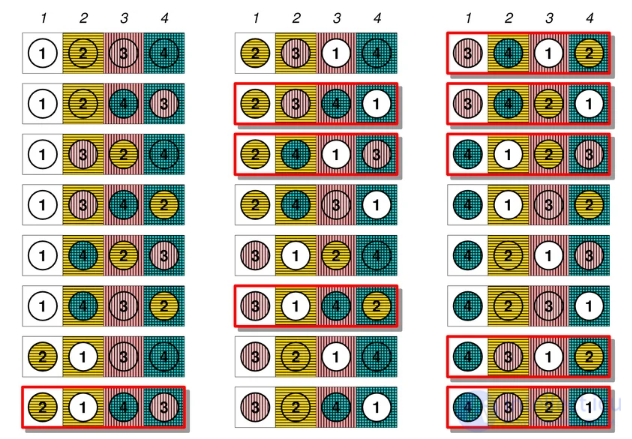
    Субфакториал в математике, понятие и применение

    Видно, что таких случаев 9, как и должно быть по формуле.Источник: https://upload.wikimedia.org/wikipedia/commons/thumb/f/f1/Derangement4.png/800px-Derangement4.png

    Судя по формуле, субфакториал всегда меньше факториала, ведь в скобках величина всегда меньшая, чем 1/2 для n>3. Поразительно, но факториал и субфакторила лаконично связаны через постоянную Эйлера, и это действительно очень красиво:

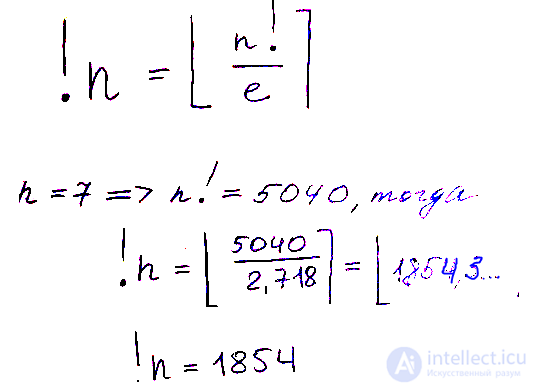
    Субфакториал в математике, понятие и применение

    Просто вычисляем ближайшее целое число к полученному результату

    Ну и напоследок еще одно феноменальное совпадение – единственное известное математикам число-субфакторион:

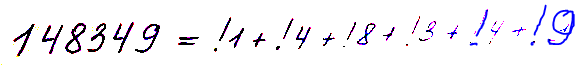
    Субфакториал в математике, понятие и применение

    Практическое применение

    Субфакториал имеет практическое применение в различных областях, таких как комбинаторика, криптография, теория графов, теория вероятностей и других. Например, в криптографии субфакториал используется для вычисления количества ключей, которые необходимы для шифрования данных, чтобы никакой ключ не использовался дважды. В теории графов субфакториал используется для определения числа гамильтоновых путей и циклов в графе.

    Также стоит отметить, что субфакториал является частным случаем обычного факториала. Факториал n обозначается как n! и определяется как произведение всех целых чисел от 1 до n. Следовательно, !n можно выразить через n! следующим образом: !n = n! * S(n, 1), где S(n, k) – количество стерлинговых чисел второго рода, которые определяют количество способов разбить множество из n элементов на k непустых подмножеств.

    • Субфакториал иногда допускается в математических играх типа получения различных результатов из определенных цифр (например, известна игра Четыре четверки, где равенство !4 = 9 может принести пользу).

    Выводы

    субфакториал – это математическая функция, которая имеет широкое практическое применение в различных областях. Знание этой функции может быть полезным для людей, работающих в таких областях, как криптография, теория графов и теория вероятностей.

    См. также

    • Факториал
    • Целочисленные последовательности

    Напиши свое отношение про субфакториал. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое субфакториал
    и для чего все это нужно, а если не понял, или есть замечания,
    то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
    Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

    Источник
    1. Mathematics
    2. Arithmetics
    3. Subfactorial

    SubFactorial Calculator !N

    Answers to Questions (FAQ)

    How to calculate a subfactorial?

    SubFactorial $ n $ is calculated using this formula: $$ !n = n! sum_{k=0}^n frac {(-1)^k}{k!} $$

    Example: $$ begin{align} !4 &= 4! ( frac{(-1)^0}{0!} + frac{(-1)^1}{1!} + frac{(-1)^2}{2!} + frac{(-1)^3}{3!} + frac{(-1)^4}{4!} ) \ &= 4! times ( 1/1 – 1/1 + 1/2 – 1/6 + 1/24 ) \ &= 24 times 9/24 \ &= 9 end{align} $$

    This formula is also used: $$ !n = left [ frac {n!}{e} right ] $$ where brackets [] stands for rounding to the closest integer.

    Example: $ 4! / e approx 24/2.718 approx 8.829 Rightarrow !4 = 9 $

    And a recurrence relationship : $$ !n = n times !(n-1) + (-1)^n $$

    What are the first values of the subfactorial function?

    The first values for the first natural numbers are:

    !1 = 0
    !2 = 1
    !3 = 2
    !4 = 9
    !5 = 44
    !6 = 265
    !7 = 1854
    !8 = 14833
    !9 = 133496
    !10 = 1334961

    see OEIS here (link)

    How to write a subfactorial?

    The subfactorial as the factorial, uses the exclamation mark as symbol but it is written to the left of the number: $ !n $

    What is the precedence of the operator subfactorial (order of operations)?

    By convention, postfixed operators have priority (the calculation goes first) over prefixed, so factorial (postfixed) has priority over subfactorial (prefixed)

    Example: $ !3! = !(3!) $

    How to calculate derangements

    Derangements (or Rencontres) are permutations without the one with fixed points (no item is in its original place). The number of derangements for $ n $ elements is subfactorial of $ n $: $ !n $.

    Example: The $ !4 = 9 $ derangements of {1,2,3,4} are {2,1,4,3}, {2,3,4,1}, {2,4,1,3}, {3,1,4,2}, {3,4,1,2}, {3,4,2,1}, {4,1,2,3}, {4,3,1,2}, and {4,3,2,1}.

    Source code

    dCode retains ownership of the “Subfactorial” source code. Except explicit open source licence (indicated Creative Commons / free), the “Subfactorial” algorithm, the applet or snippet (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or the “Subfactorial” functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) and all data download, script, or API access for “Subfactorial” are not public, same for offline use on PC, mobile, tablet, iPhone or Android app!
    Reminder : dCode is free to use.

    Cite dCode

    The copy-paste of the page “Subfactorial” or any of its results, is allowed (even for commercial purposes) as long as you cite dCode!
    Exporting results as a .csv or .txt file is free by clicking on the export icon
    Cite as source (bibliography):
    Subfactorial on dCode.fr [online website], retrieved on 2023-05-17, https://www.dcode.fr/subfactorial

    Источник

    Приветствую Вас, уважаемые Читатели! Итак, сегодня хочу рассказать об удивительном математическом зоопарке факториалов. Оказывается, кроме привычной для всех операции, есть еще целых 8 вариантов. Поехали!

    1. Факториал

    Возникает естественным образом в комбинаторике – науке, в которой изучаются задачи, связанные с выбором и расположением различных элементов чаще всего конечных множеств.

    2. Двойной факториал

    Этот факториал имеет просто громадное количество приложений в комбинаторике и достоин отдельного материала. Впервые он использовался при выводе замечательного произведения Уоллиса, связывающего натуральные числа и число π:

    3. Субфакториал

    Этот представитель семейства в отличие от обычного факториала, который определяет количество перестановок, определяет количество беспорядков. 

    Дальше – математическая экзотика

    4. Праймориал

    Определяется как произведение простых чисел, меньших или равных данному. Подробная информация и особенности его применения – здесь.

    5. Суперфакториал Слоуна

    Название дано создателем уникальной в своём роде Онлайн Энциклопедии Целочисленных Последовательностей (OEIS). Определяется как произведение факториалов чисел, меньших или равных заданному.

    6. Суперфакториал Пиковера

    Запись показателя степени слева сверху от числа определяет особенную математическую операцию – тетрацию

    Удивительно быстрорастущая функция. Для числа 3 – это уже вот такая невообразимая башня:

    Степени “схлопываются” справа-налево

    7. Экспоненциальный факториал

    По сравнению с предыдущим представителем растет “медленно”. Например, для выражения выше – это 262144. Правда, для числа 6 в результате уже 10^183230 нулей.

    8. Гиперфакториал

    Растет еще медленнее, чем предшествующие два. Только лишь на 14 шаге число нулей приближается к гуголу.

    9. Фиббоначиал (бонус)

    Равняется произведению первых n чисел Фибоначчи.

    P.S. Кроме перечисленных существуют еще возрастающие и убывающие факториалы, но они являются частным случаем факториала обычного.

    Источник

    Добавить комментарий