Последовательность — высокоупорядоченный числовой набор, образованный по заданному закону. Термин «ряд» обозначает результат сложения членов соответствующей ему последовательности. Для различных числовых последовательностей мы можем найти сумму всех ее членов или общее число элементов до заданного предела.
Последовательность
Под этим термином понимается заданный набор элементов числового пространства. Каждый математический объект задается определенной формулой для определения общего элемента последовательности, а для большинства конечных числовых наборов существуют простые формулы определения их суммы. Наша программа представляет собой сборник из 8 онлайн-калькуляторов, созданных для вычисления сумм наиболее популярных числовых наборов. Начнем с самого простого — натурального ряда, которым мы пользуемся в повседневной жизни для пересчета предметов.
Натуральная последовательность
Когда школьники изучают числа, они первым делом учатся считать предметы, например, яблоки. Натуральные числа естественным образом возникают при счете предметов, и каждый ребенок знает, что 2 яблока — это всегда 2 яблока, не больше и не меньше. Натуральный ряд задается простым законом, который выглядит как n. Формула гласит, что n-ный член числового набора равен n: первый — 1, второй — 2, четыреста пятьдесят первый — 451 и так далее. Результат суммирования n первых натуральных чисел, то есть начинающихся от 1, определяется по простой формуле:
∑ = 0,5 n × (n+1).
Благодаря этому выражению легко рассчитать конечную сумму натурального ряда от 1 до n. Очевидно, что натуральная последовательность стремится в бесконечность, поэтому, чем больше n, тем больше конечный результат.
Расчет суммы натурального ряда
Для вычислений вам потребуется выбрать в меню калькулятора формулу натурального ряда n и ввести количество членов последовательности. Давайте вычислим сумму натурального ряда от 1 до 15. Указав n = 15, вы получите результат в виде самой последовательности:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
и суммы натурального ряда, равной 120.
Легко проверить корректность вычислений при помощи выше приведенной формулы. Для нашего примера результат сложения будет равен 0,5 × 15 × 16 = 0,5 × 240 = 120. Все верно.
Последовательность квадратов
Квадратичная последовательность образуется из натуральной, путем возведения каждого члена в квадрат. Ряд квадратов формируется по закону n2, следовательно, n-ный член последовательности будет равняться n2: первый — 1, второй — 22 = 4, третий — 32 = 9 и так далее. Результат суммирования начальных n элементов квадратичной последовательности вычисляется по закону:
∑ = (n × (n+1) × (2n+1)) / 6.
При помощи этой формулы вы легко можете высчитать сумму квадратов от 1 до n для сколько угодно большого n. Очевидно, что эта последовательность также бесконечна и с ростом n будет расти и общее значение числового набора.
Расчет суммы квадратного ряда
В этом случае вам потребуется выбрать в меню программы закон квадратной последовательности n2, после чего выбрать значение n. Давайте рассчитаем сумму первых десяти членов последовательности (n= 10). Программа выдаст саму последовательность:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
а также сумму, равную 385.
Кубический ряд
Ряд кубов представляет собой последовательность натуральных чисел, возведенных в куб. Закон образования общего элемента последовательности записывается как n3. Таким образом, первый член ряда равен 13 = 1, второй — 23 = 8, третий — 33 = 27 и так далее. Сумма первых n элементов кубического ряда определяется по формуле:
∑ = (0,5 n × (n+1))2
Как и в предыдущих случаях, элементы числового пространства стремятся в бесконечность, и чем больше количество слагаемых, тем больше результат суммирования.
Расчет суммы кубического ряда
Для начала выберите в меню калькулятора закон кубического ряда n3 и задайте любое значение n. Давайте определим сумму ряда из 13 членов. Калькулятор выдаст нам результат в виде последовательности:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197
и суммы соответствующего ей ряда, равного 8281.
Последовательность нечетных чисел
Множество натуральных чисел содержит подмножество нечетных элементов, то есть тех, которые не делятся на 2 без остатка. Последовательность нечетных чисел определяется выражением 2n — 1. Согласно закону, первый член последовательности будет равен 2×1 − 1 = 1, второй — 2×2 − 1 = 3, третий — 2×3 − 1 = 5 и так далее. Сумма начальных n элементов нечетного ряда вычисляется по простой формуле:
∑ = n2.
Рассмотрим пример.
Вычисление суммы нечетных чисел
Сначала выберете в меню программы закон образования нечетного ряда 2n−1, после чего введите n. Давайте узнаем первые 12 членов нечетной ряда и его сумму. Калькулятор мгновенно выдаст результат в виде набора чисел:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23,
а также суммы нечетного ряда, который равен 144. И действительно, 122 = 144. Все верно.
Прямоугольные числа
Прямоугольные числа относятся к классу фигурных чисел, которые представляют собой класс числовых элементов, необходимых для построения геометрических фигур и тел. К примеру, чтобы построить треугольник необходимо 3, 6 или 10 точек, квадрат — 4, 9 или 16 точек, а для выкладывания тетраэдра потребуется 4, 10 или 20 шаров или кубов. Прямоугольники легко построить при помощи двух последовательных чисел, например, 1 и 2, 7 и 8, 56 и 57. Прямоугольные же числа выражаются в виде произведения двух последовательных натуральных чисел. Формула для общего члена ряда выглядит какn × (n+1). Первые десять элементов такого числового набора выглядят как:
2, 6, 12, 20, 30, 42, 56, 72, 90, 110…
С увеличением n растет и значение прямоугольных чисел, следовательно, сумма такого ряда также будет расти.
Обратная последовательность
Для прямоугольных чисел существует обратная последовательность, определяемая формулой 1 / (n × (n+1)). Числовой набор трансформируется в набор дробей и выглядит как:
1/2 , 1/6, 1/12, 1/20, 1/30, 1/42, 1/56, 1/72, 1/90, 1/110…
Сумма ряда дробей определяется по формуле:
∑ = 1 — 1/(n+1).
Очевидно, что при увеличении количества элементов ряда значение дроби 1/(n+1) стремится к нулю, а результат сложения приближается к единице. Рассмотрим примеры.
Сумма прямоугольного и обратного ему ряда
Давайте рассчитаем значение прямоугольной последовательности для n = 20. Для этого выберете в меню онлайн-калькулятора закон задания общего члена числового набора n × (n+1) и укажите n. Программа выдаст мгновенный результат в виде 3080. Для вычислений обратного ряда измените закон на 1 / (n × (n+1)). Сумма обратных числовых элементов будет равна 0,952.
Ряд произведений трех последовательных чисел
Прямоугольный числовой набор можно изменить, добавив к нему еще один последовательный множитель. Следовательно, формула для вычисления n-ного члена набора преобразится в n × (n+1) × (n+2). Согласно этой формуле элементы ряда образуются в виде произведения трех последовательных чисел, например, 1 × 2 × 3 или 10 × 11 × 12. Первые десять элементов такого ряда выглядят как:
6, 24, 60, 120, 210, 336, 504, 720, 990, 1320
Это быстрорастущий числовой набор, а сумма соответствующего ряда при росте n уходит в бесконечность.
Обратная последовательность
Как и в предыдущем случае, мы можем обратить формулу n-ного члена и получить выражение 1 / (n × (n+1) × (n+2)). Тогда набор целых значений преобразится в ряд дробей, в знаменателе которых будут стоять произведения трех последовательных чисел. Начало такого набора имеет следующий вид:
1/6, 1/24, 1/60, 1/120, 1/210, 1/336…
Сумма соответствующего ряда определяется по формуле:
∑ = 0,5 × (0,5 — 1 / (n+1) × (n+2)).
Очевидно, что при росте количества элементов дробь 1 / ((n+1) × (n+2)) стремится к нулю, а сумма ряда приближается к значению 0,5 × 0,5 = 0,25. Рассмотрим примеры.
Ряд произведений трех последовательных чисел и обратный ему
Для работы с этим набором требуется выбрать закон определения общего элемента n × (n+1) × (n+2) и задать n, к примеру, 100. Калькулятор выдаст вам саму последовательность, а также значение результата сложения сотни чисел, равный 26 527 650. Если выбрать обратный закон 1 / (n × (n+1) × (n+2)), сумма ряда из 100 членов будет равна 0,250.
Заключение
Сборник калькуляторов позволяет рассчитать сумму восьми наиболее популярных последовательностей. Пользуйтесь нашим сервисом для решения учебных заданий по математике или программированию.
Содержание:
- 0.1 тЕЫЕОЙЕ
- 0.2 пФЧЕФ
- 0.3 йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
- 1 Другие интересные вопросы и ответы
- 1.1 Какое среднее число между нулём и бесконечностью?
дБОЩ 6 ГЙЖТ: 0, 1, 2, 3, 4, 5. оБКФЙ УХННХ ЧУЕИ ЮЕФЩТЈИЪОБЮОЩИ ЮЈФОЩИ ЮЙУЕМ, ЛПФПТЩЕ НПЦОП ОБРЙУБФШ ЬФЙНЙ ГЙЖТБНЙ (ПДОБ Й ФБ ЦЕ ГЙЖТБ Ч ЮЙУМЕ НПЦЕФ РПЧФПТСФШУС).
тЕЫЕОЙЕ
вХДЕН ПФДЕМШОП РПДУЮЙФЩЧБФШ УХННХ ФЩУСЮ, УПФЕО, ДЕУСФЛПЧ Й ЕДЙОЙГ ДМС ТБУУНБФТЙЧБЕНЩИ ЮЙУЕМ. оБ РЕТЧПН НЕУФЕ НПЦЕФ УФПСФШ МАВБС ЙЪ РСФЙ ГЙЖТ 1, 2, 3, 4, 5. лПМЙЮЕУФЧП ЧУЕИ ЮЙУЕМ У ЖЙЛУЙТПЧБООПК РЕТЧПК ГЙЖТПК ТБЧОП 6·6·3 = 108, РПУЛПМШЛХ ОБ ЧФПТПН Й ФТЕФШЕН НЕУФЕ НПЦЕФ УФПСФШ МАВБС ЙЪ ЫЕУФЙ ГЙЖТ, Б ОБ ЮЕФЧЈТФПН НЕУФЕ – МАВБС ЙЪ ФТЈИ ГЙЖТ 0, 2, 4. рПЬФПНХ УХННБ ФЩУСЮ ТБЧОБ (1 + 2 + 3 + 4 + 5)·108·1000 = 1620000. лПМЙЮЕУФЧП ЮЙУЕМ У ЖЙЛУЙТПЧБООПК ЧФПТПК ГЙЖТПК ТБЧОП 6·3 = 90 (ОБ РЕТЧПН НЕУФЕ УФПЙФ МАВБС ЙЪ РСФЙ ГЙЖТ). рПЬФПНХ УХННБ УПФЕО ТБЧОБ
(1 + 2 + 3 + 4 + 5)·90·100 = 135000. бОБМПЗЙЮОП УХННБ ДЕУСФЛПЧ ТБЧОБ 13500, Б УХННБ ЕДЙОЙГ – (2 + 4)·5·6·6 = 1080.
пФЧЕФ
йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
| ПМЙНРЙБДБ | |
| оБЪЧБОЙЕ | нПУЛПЧУЛБС НБФЕНБФЙЮЕУЛБС ПМЙНРЙБДБ |
| ЗПД | |
| оПНЕТ | 8 |
| зПД | 1945 |
| ЧБТЙБОФ | |
| лМБУУ | 7,8 |
| фХТ | 2 |
| ЪБДБЮБ | |
| оПНЕТ | 1 |
рТПЕЛФ ПУХЭЕУФЧМСЕФУС РТЙ РПДДЕТЦЛЕ Й .
Я не занимаюсь составлением программ и помнить формулы прогрессий тоже не в состоянии. Однако найти сумму всех трехзначных чисел не сложно. надо просто скомбинировать их правильным образом. Для начала отбросим число 100 и 550, которые пригодятся на последнем этапе подсчета. Потом обратим внимание, что 101+999 = 1100. Такая же сумма будет у всех остальных пар чисел до 549+551. Остается определить, сколько же пар чисел мы имеем 549-100 = 449. Теперь просто умножаем 449 на 1100, и добавляем к этому произведению отброшенные ранее числа 100 и 550. Получается 494550.
Только не надо путаться и добавлять 1000 – это уже четырехзначное число.
Другие интересные вопросы и ответы
Какое среднее число между нулём и бесконечностью?
Отвечу анекдотом: Поймали инопланетяне русского, американца и француза. И говорят: “Отпустим того, кто назовёт такое число, которого мы не знаем”. Американец подумал-подумал и говорит: “миллиард” Инопланетяне: “А, это мы знаем, столько планет в галактике” Француз подумал и говорит: “триллион” “А, ну это мы знаем. Столько звёзд на небе” Русский думает-думает и говорит: “дохрена” “Ого,- удивляются инопланетяне,- а это сколько?” “Ну вот вы приезжайте к нам в Россию, идите по железной дороге и считайте шпалы. Вот как только будет “да нахрен нам все это надо?” – так это и будет ровно половина”
У Вас недостаточно прав для добавления комментариев.
Вам необходимо зарегистрироваться на сайте
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
Instant Solution:
Step 1/2
First, we need to determine the range of four-digit positive integers. The smallest four-digit integer is 1000, and the largest is 9999.
Now, we can use the arithmetic series formula to find the sum of all the integers in this range. The formula is:
Sum = (n * (first + last)) / 2
where n is the number of terms in the series, first is the first term, and last is the last term.
Textbook Answer
Video by Joshua Eastwood
Numerade Educator
This textbook answer is only visible when subscribed! Please subscribe to view the answer
Формулы последовательностей:
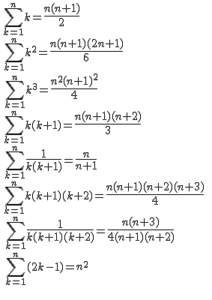
где k — порядковый номер;
n — количество членов.
Рассмотрим варианты быстрого нахождения суммы разного количества последовательных чисел.
1 вариант. Для того, чтобы определить сумму 5-ти последовательных чисел, следует умножить на 5 число, находящее посередине:
(х — 2) + (х — 1) + (х) + (х + 1) + (х + 2) = 5х,
в данном выражении х — число, находящееся посередине.
Например, сумма 30 + 31 + 32 + 33 + 34 будет равна 32 х 5 = 160
2 вариант. Чтобы найти сумму 5-ти последовательных чисел, нужно:
— умножить на 5 наибольшее число;
— из полученного произведения вычесть 10.
Возьмем, к примеру, те же 5 последовательных цифр 30,31,32,33,34
Дальше: 34 х 5 = 170
170 — 10 = 160
3 вариант. Чтобы найти сумму 5 последовательных чисел, можно:
— умножить на 5 наименьшее число;
— К полученному результату прибавить 10.
Взяв в качестве примера предыдущую последовательность:
30 х 5 = 150
150 + 10 = 160
Чтобы вычислить сумму 4-х последовательных чисел, нужно:
— умножить наибольшее число на 4;
— из полученного произведения вычесть 6.
Чтобы определить сумму 6 последовательных чисел, необходимо:
— умножить на 6 наибольшее число;
— от результата отнять 15.
Чтобы рассчитать сумму 7 последовательных чисел, нужно:
— умножить на 7 наибольшее число;
— вычесть из полученного произведения 21.
Чтобы вычислить сумму 8 последовательных чисел:
— умножим на 8 наибольшее число;
— из произведения вычесть 28.
Чтобы сложить любое количество как четных, так и нечетных последовательных чисел, нужно:
— сложить первое и последнее числа последовательности;
— полученный результат делим на 2;
— затем умножаем на число последовательных чисел, что выразим формулой:
n х (a+b)/2.
Чтобы быстро и правильно рассчитать сумму последовательности, воспользуйтесь онлайн калькулятором. Для этого вам нужно лишь выбрать последовательность и число членов последовательности.
Расчет суммы последовательности из приведенных последовательностей и количества членов
Содержание:
- Понятие суммы ряда
- Вычисление суммы ряда почленным интегрированием
- Вычисление суммы ряда почленным дифференцированием
Понятие суммы ряда
Постановка задачи. Найти сумму ряда

где  — целые числа.
— целые числа.
План решения. Суммой ряда  называется предел
называется предел  последовательности его частичных сумм
последовательности его частичных сумм  , т.е.
, т.е.

где 
1. По условию задачи

Если корни знаменателя различаются на целое число, т.е. 
 где
где  — натуральное число, то члены последовательности частичных сумм ряда
— натуральное число, то члены последовательности частичных сумм ряда  легко найти, так как в выражении
легко найти, так как в выражении  многие слагаемые взаимно уничтожаются.
многие слагаемые взаимно уничтожаются.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:

и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим  -ю частичную сумму ряда:
-ю частичную сумму ряда:
 ,
,
сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)

и записываем ответ.

Пример:
Найти сумму ряда

Решение:
1. Корни знаменателя  и
и  различаются на целое число, т.е.
различаются на целое число, т.е.  Следовательно, члены последовательности частичных сумм ряда
Следовательно, члены последовательности частичных сумм ряда  легко найти, так как в выражении
легко найти, так как в выражении  многие слагаемые взаимно уничтожаются.
многие слагаемые взаимно уничтожаются.
2. Разлагаем общий член ряда на элементарные дроби

и выписываем несколько членов ряда:


3. Сокращая все слагаемые, какие возможно, находим  -ю частичную сумму ряда:
-ю частичную сумму ряда:

4. Вычисляем сумму ряда по формуле (1):

Ответ: 
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством

Если  , ряд расходится. Если
, ряд расходится. Если  , ряд сходится условно (по признаку Лейбница). Следовательно, область сходимости определяется неравенствами
, ряд сходится условно (по признаку Лейбница). Следовательно, область сходимости определяется неравенствами 
2. Делаем в исходном ряде замену  , получим степенной ряд
, получим степенной ряд

с областью сходимости  .
.
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем

Заметим, что так как ряд (1) сходится в граничной точке  , то сумма ряда непрерывна в этой точке (справа). Следовательно,
, то сумма ряда непрерывна в этой точке (справа). Следовательно, 
6. Вычисляем интеграл, делаем замену  на
на  и записываем ответ: сумму ряда и область его сходимости.
и записываем ответ: сумму ряда и область его сходимости.
Замечание. Если ряд имеет вид

то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:

и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда

и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 
В граничных точках при  ряд расходится, при
ряд расходится, при 
 ряд сходится условно.
ряд сходится условно.
Следовательно, данный ряд сходится при всех 
 .
.
2. Сделаем замену  Получим геометрический ряд (1) с областью сходимости
Получим геометрический ряд (1) с областью сходимости 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке  , целиком принадлежащем интервалу сходимости, и используя формулу (4), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (4), получаем

Заметим, что так как ряд (1) сходится в граничной точке  , то его сумма непрерывна в этой точке (справа). Следовательно, формула (5) справедлива при всех
, то его сумма непрерывна в этой точке (справа). Следовательно, формула (5) справедлива при всех  .
.
6. Заменяя  на
на  , получаем при
, получаем при 

Ответ. 
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством

Если  , ряд расходится (не выполнено необходимое условие сходимости). Следовательно, область сходимости определяется неравенствами
, ряд расходится (не выполнено необходимое условие сходимости). Следовательно, область сходимости определяется неравенствами  .
.
2. Делаем в исходном ряде замену  и записываем его в виде суммы двух рядов
и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов
 и
и 
3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем

6. Вычисляем производную и делаем замену  на
на  . Записываем ответ: сумму ряда и область его сходимости.
. Записываем ответ: сумму ряда и область его сходимости.
Замечание. Если ряд имеет вид

то вычисляем сумму трех рядов, причем при вычислении суммы ряда

применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда

и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством  . Отсюда
. Отсюда  . В граничных точках
. В граничных точках  ряд расходится, так как не выполнено необходимое условие сходимости. Следовательно, ряд сходится в интервале
ряд расходится, так как не выполнено необходимое условие сходимости. Следовательно, ряд сходится в интервале  .
.
2. Делаем в исходном ряде замену  и записываем его в виде суммы двух рядов
и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов

3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:

Следовательно,  при всех
при всех  .
.
4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем

Таким образом,

Заменяя  на
на  , получим
, получим

Ответ. 


Лекции:
- Метод Якоби
- Метод интегрирования
- Свойства функций, имеющих конечный предел
- Дифференциал длины дуги кривой. Формула парабол
- Дифференциальное уравнение Бернулли
- Область сходимости ряда
- Метод Ритца
- Разложение в ряд фурье функций
- Построение графиков функции с помощью производной
- Формулы двойного угла
